В настоящее время российской туристский рынок находится в завершающей фазе структуризации. Происходит разделение его участников на оптовых и розничных игроков : туроператоров и турагентов. В данной работе рассматривается рынок туроператоров, то есть компаний, имеющих деловые отношения на основе контрактов: с туробъектами (музеями, галереями, театрами), с ведущими авиакомпаниями и другими организациями, предоставляющими транспортные и прочие услуги.

На конкурентном поле намечаются следующие тенденции:

• •    рынок испытывает процесс консолидации. На каждом направлении выделяется 3-5 компаний, контролирующих большую часть рынка.

• •    происходит диверсификация туристического рынка . Происходит переход от узкой специализации по направлениям к широкому спектру предлагаемых услуг.

• •    сокращается количество независимых туристических агентств и увеличивается доля турагентских сетей

• •    крупные туроператоры применяют франчайзинговые схемы работы.

• •    на рынке растёт конкуренция, которая способствует созданию монополий, так как

the model of the "predator-victim", phase portrait.

каждый конкурент на туристском рынке мечтает стать монополистом.

В России создана и действует Ассоциация туроператоров, включающая 47 туроператорских компаний, которые, по экспертным оценкам, в 2010 году обслужили более 7 млн туристов во всех сегментах туристического рынка. Совокупный оборот операторов-членов АТОР в 2010 году составил около 9 млрд долларов. По данным Ростуризма из них12 туроператоров с финансовым обеспечением более 100 млн руб.

Единый федеральный реестр представил данные по финансовому обеспечению туроператоров за 2011 год – таблица 2.

Рынок туроператоров – это рынок монополистической конкуренции с небольшой группой явных лидеров. Как любая сложная социально-экономическая система, этот рынок развивается в результате действий многочисленных игроков, имеющих собственные цели, а также случайных факторов. Происходит типичный процесс конфликта интересов, математической моделью которого является дифференциальная игра N лиц. Такой динамичной системе свойственны сложные типы поведения: ограниченность роста, мультистабильность, периодические и квазистохастические измене-

Название туроператора	Финансовое обеспече-ние,млн рублей	Примечание
Пегас туристик	164,9	Основан 1994 год
Тез тур	100,0	Основан 1994 год
Верса	351,5	Основан 1994 год
Корал тревел	100,0	Основан 1995 год. Состоит в международном холдинге OTI
НТК Интурист	100,0	Глобальный комплект НТК Интурист соединил в себе четыре крупнейшие компании, войдя на российский туристический рынок в 2007 году компания наделена собственными колоссальными ресурсами – авиа-брокерской компанией, отелями и гостиницами как в России, так и за рубежом.
Асент тревел	161,0	Основан 1994 год. В 2007 году Асент Тревел входит в состав крупнейшего европейского холдинга HotelPlan Group
Сольвекс	298,0	Основана 1993 год.
Нева	442,1	Основана 1990 год. Один из учредителей Ассоциации Туроператоров России, официальный турагент Администрации Санкт- Петербурга и член Международной Ассоциации Воздушного Транспорта.
TUI	105,4	Основан 1994 год

ния переменных, характеризующих развивающуюся систему. века для объяснения периодических изменений числа особей. В зависимости от выбора коэффициентов модель описывает либо борьбу ви- Таблица 1. Данные Ростуризма по наиболее дов за общий ресурс, либо взаимодействие типа крупным туроператорам

Основными проблемами в дифференциальных играх N лиц являются выработка принципа оптимальности (определение того, что является оптимальным поведением), доказательство его существования и поиск аналитических методов или численных алгоритмов нахождения оптимального решения.

При анализе рынка туроператоров и составления математической модели можно применить классическую модель взаимодействия видов, которая впервые была предложена А.Лоткой и В.Вольтерра в тридцатые годы XX хищник – жертва, когда один вид является пищей для другого [2]. В данном случае в роли хищника можно рассматривать крупные компании, а в роли жертвы – средние и малые туристские фирмы.

Таблица 2. Финансовое обеспечение туроператоров за 2011 год

Данные Единого федерального реестра туроператоров	Количество туроперато-ров,ед
100 и более млн рублей	37
60 млн рублей	35
30 млн рублей	2241
10 млн рублей	122
550-1500 тысяч рублей	11
500 тысяч рублей	1960

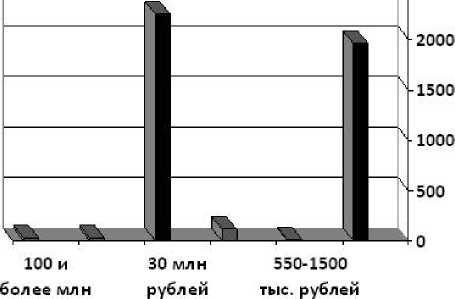
рублей

Рисунок 1. Гистограмма, построенная на статистике финансового обеспечения туроператоров

В основу предложенного моделирования положены следующие идеализированные представления о характере внутривидовых и межвидовых отношений в системе хищник-жертва [1]:

• 1)    В отсутствии хищника популяция жертвы размножается в соответствии с принципом Мальтуса – экспоненциально;

• 2)    Популяция хищника в отсутствии жертвы экспоненциально вымирает;

• 3)    Суммарное количество жертвы, потребляемое популяци ей хищника в единицу времени, линейно зависит и от плотности популяции жертвы, и от плотности популяции хищника;

• 4)    Потребленная хищником биомасса жертвы с постоянным коэффициентом перерабатывается в биомассу хищника;

  Математическое моделирование рынка туроператоров на основе системы «хищник-жертва»

  
  

  5) Какие бы то ни было дополнительные факторы, влияющие на динамику популяции отсутствуют.

  Рассматриваем случай, когда крупная компания является хищником, а малая — жертвой, и будем считать, что хищник питается только жертвой.

  Пусть х ( t ) и y ( t ) - численность жертв

  
  

  и хищников соответственно. допустим, что единственным лимитирующим фактором, ограничивающим размножение жертв, является давление на них со стороны хищников, а размножение хищников ограничивается количеством добытой ими пищи (количеством жертв). Тогда в отсутствии хищников численность жертв должна расти экспоненциально с относительной скоростью а , а хищники в отсутствии

  
  

  ства, производитель направляется в отрасли и регионы, где они могут быть применены наиболее эффективно). Аналогичный вид будет иметь трофическая функция, если жертвы могут вырабатывать защитную стратегию (например, прятаться в убежище, недоступное хищникам). Динамическое поведение системы в значительной степени зависит от вида трофической функции. По нашему мнению для исследуемой проблемы наиболее характерны первый и третий тип трофической функции.

  
  

  жертв - также экспоненциально вымирать с относительной скоростью m . Коэффициенты а и m - коэффициенты естественного прироста жертв и естественной смертности хищников соответственно.

  Пусть V = V ( х ) - количество жертв, потребляемых одним хищником за единицу времени, причем к -ая часть полученной с это-

  
  
  

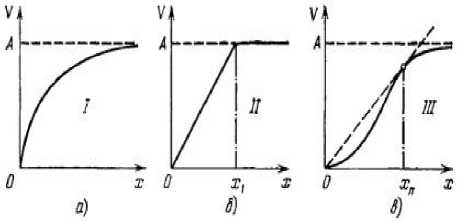
  Рисунок 2. Различные типы трофических функций в системе хищник-жертва

  
  

  го количества энергии расходуется хищником

  
  

  на воспроизводство, а остальное тратится на поддержание основного обмена и охотничьей активности.

  
  

  Тогда уравнение системы

  
  

  хищник-

  
  

  жертва можно записать в виде:

  
  

  Рассмотрим ситуацию малых значений х . При малых значениях х , например, когда трофические отношения в системе напряжены и почти все жертвы становятся добычей хищника, который всегда голоден и насыщение не наступает (ситуация довольно обычная в природе), трофическую функцию V ( х ) можно считать линейной функцией численности жертв, т.е. V = в х . Кроме того, предположим,

  
  

  <

  
  

  dx

  
  

  — = а х

  
  

  dt

  
  

  V ( ^х ) У

  
  

  что к = const . Тогда:

  
  

  dy

  I it

  
  
  
  

  y ( kV ( х ) - m )

  
  
  
  

  Функцию V ( х ) обычно называют трофической функцией хищника или функциональным откликом хищника на плотность популяции жертвы. Именно эти функции обычно определяются в экспериментальных работах, посвященных изучению хищничества, и к настоящему времени считается установленным, что эти функции обычно принадлежат к одному из следующих трех типов (рис.2) [3].

  Первый тип характерен, например, для беспозвоночных и некоторых видов хищных рыб (в нашем случае этап хищнического накопления капитала). Второй тип - это трофическая функция с резко выраженным порогом насыщения, характерная для хищников-фильтратов. Тритий тип характерен, для позвоночных - организмов, проявляющих достаточно сложное поведение (в нашем случае оптимизация использования всех факторов производ

  
  

  dx

  It^=ах - ^вхУ

  dy

  — = к в ху - my .

  
  
  
  

  Система с точностью до обозначений совпадает с классической моделью В.Вольтерра, который показал, что эта система имеет интеграл вида

  г „ xv г yY а

  
  

  —

  V X

  
  

  ^е-

  J I ^Y J

  
  

  = C ,

  
  
  
  

  где: X = х/х *; Y = y/y *; х * = m/k p , у * = а в .

  
  

  Если х ₀ , у ₀ - начальные значения численностей жертв и хищников соответственно, то

  
  

  C =

  
  

  ( рх о/ х * Y

  V ^х 0 / ^х J

  
  

  ' e о/ у * а ^а v у о! у * ,

  
  

  > о

  
  
  
  

  и уравнение (3) описывает семейство вложен

  
  

  ных друг в друга замкнутых кривых, соответ-

  
  

ствующих фазовым траекториям периодических решений системы (2). Заметим, что при увеличении C амплитуды колебаний x и y возрастают (рис. 3).

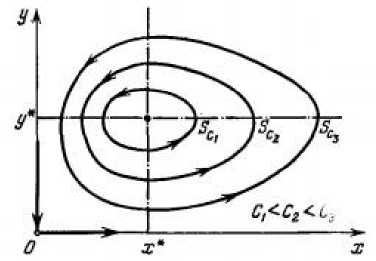
Рисунок 3. Фазовый портрет классической вольтеровской системы хищник-жертва

( ^{m +a} )

При минимальномзначении C * = e ' эти кривые стягиваются в точку с координатами ( x *, у * ) . Легко видеть, что x * = m/k p и у * = а в являются решениями системы (2) при dx)dt = dy|dt = 0 , т.е. ее нетривиальным равновесием. Для случая малых колебаний возле этого состояния ( p = x - x *, q = у - у * ) уравнения модели можно записать в виде:

dp =- mq , dq = k a p . (5) dtk ^, dt

Корни соответствующего характеристического уравнения есть 2 1 ₂ =± i-Jam , т.е. точка ( x , у ) - центр. Период малых колебаний T = 2 n(4am , причем колебания численности одного вида сдвинуты по фазе относительно колебаний другого на п /2.

В системе имеется еще одно положение равновесия – начало координат. Нетрудно видеть, что эта точка – седло. Оси координат являются сепаратрисами, причем ось Oy входит в седло, а ось Ox – выходит из него.

Очевидно, что характер изменения состояния ( x, y ) определяется значениями параметров. Изменяя эти параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния системы.

Несмотря на то, что модель Вольтерра смогла объяснить многие реально наблюдав- шиеся явления, у нее есть большой недостаток – негрубость (в математическом смысле этого слова) вольтерровских циклов, так что при любых сколь угодно слабых возмущениях фазовых координат система переходит с одного цикла на другой. Отсутствие асимптотической устойчивости равновесия указывает на то, что в вольтеровской системе отсутствуют механизмы, стремящиеся сохранить ее нетривиальное равновесное состояние.

Выводы:

• •    простейшая модель «хищник-жертва» может применяться для моделирования рынка туроператоров и динамики конкурентной борьбы за ресурсы и за потребителя

• •    при моделировании использовался метод аналогии с биологическими сообществами, представленный моделью «хищник-жертва». Предполагается, что конкурируют туроператоры, поставляющие на рынок однотипную продукцию.

• •    конкурентная борьба за ресурсы и за потребителя описывается системой двух дифференциальных уравнений, типичной для модели «хищник‒жертва». Параметры системы характеризуют чувствительность к недостатку рeсурса, к динамике спроса на продукцию фирм

• •    в работе рассмотрен случай существования двух стационарных точек системы дифференциальных уравнений модели; исследована устойчивость движения в окрестности стационарной точки.

• •    при неограниченной конкуренции система является абсолютно неустойчивой и в ней происходит неограниченная концентрация ресурсов. Эффективным методом поддержания динамического равновесия может служить политика государства в роли «охотника».