Математическое моделирование силового взаимодействия щеток коммунальных машин с дорожным покрытием

При взаимодействии цилиндрической щетки с дорожным покрытием ее ворс изгибается упруго, а затем распрямляется, преодолевая силы трении, и совершает свободные колебания. Колебания, возникающие в этих условиях, носят название автоколебаний. В первой стадии процесса автоколебаний происходит подбрасывание твердых частиц загрязнений над поверхностью покрытия силами упругости ворса и последующее засасывание их воздуховсасывающим агрегатом коммунальной уборочной машины, либо удаление их специальным транспортером.

Эффективность процесса уборки при этом зависит от процесса силового взаимодействия ворса щетки с дорожным покрытием, которые определяются свойствами покрытия и ворса (геометрическими и механическими), характеристиками контактного взаимодействия (скоростью скольжения, частотой вра- щения щетки, величиной деформации каждой ворсины, находящейся в условиях контактного взаимодействия).

Геометрические характеристики ворса [1] определяются условиями их установки на подметальные машины и условиями эксплуатации щетки в зимнее и летнее время. Так для пластмассовой (полипропиленовой щетки) из условий эксплуатации подобраны для летнего времени средняя толщина ворса 1,5 – 2,3 мм, а для зимнего – толщина 2,8 ÷ 3,2 мм. Это обусловлено тем, что производительность процесса при уборке снега, как правило, требуется большая, чем при подметании дорожного покрытия в летнее время. Хотя исключением может быть уборка мусора при проведении строительных работ, где применяют щетки с толщиной ворса 4 и более миллиметров.

Условия установки щетки на подметальную машину определяют диаметр подметального диска цилиндрической щетки (определяется дорожным просветом автомобиля) и ее длину (определяется шириной автомобиля). Так оптимальными для установки на большинство автомобилей отечественного и импортного производства на сегодняшний день опре- делены щетки наружным диаметром D =550 мм. Такая щетка [1] имеет ступицу диаметром d = 180 мм и набирается на вал, диаметром dB =78 мм.

Как правило, щетку набирают из ворса, который имеет овальное попереч- ное сечение и некоторую волнистость по длине. Эти особенности геометрии получаются в процессе изготовления методом экструзии при взаимодействии со специальными валками и предназначены способствовать процессу подметания за счет оптимизации продольной и поперечной упругости щеточного ворса. Т.е. – снижения продольной и увеличения поперечной жесткости (рис.1).

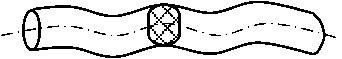
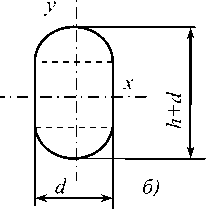
Рисунок 1 – Геометрия щеточного ворса: а) – продольная волнистость; б) – поперечное сечение

Скорость скольжения ворса по дорожному покрытию определяется [1] cкоростью движения автомобиля ^авт в зимнее и летнее время, которые в среднем составляют 13 и 6 км/час соответственно, а также частотой вращения вала щетки современных машин, которая достигает n = 270 ÷ 300 об\мин. При этом средняя линейная скорость скольжения ворса будет достигать величины Vc =11.8 м\с зимой и vc =9.8 м\с в летнее время при значении ее наружного диаметра D=550 мм.

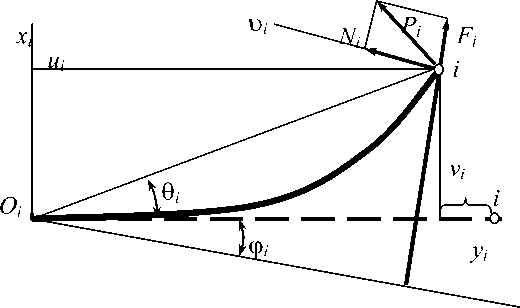
Величину деформации каждой ворсины, находящейся в условиях контактного взаимодействия будет опреде- лять в первую очередь вертикальное смещение оси щетки относительно точки касания его с дорожным покрытием 5.

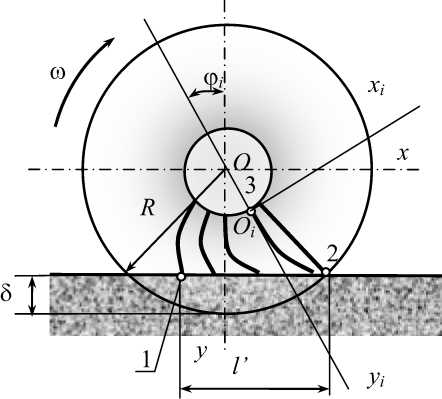
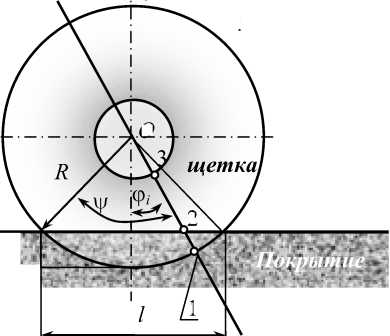
Зависимость между длиной контакта цилиндрической щетки и смещением 5 можно определить исходя из простых геометрических соотношений, определенных в системе координат xOy (рис.2).

Iy x2+ y2  R2i=0

x y=tg(90+Ф i)

*■ ■>

О

Рисунок 2 – Схема взаимодействия щетки с дорожным покрытием

x² + у² — 7?² = 0; . у = —R + 5;

Z² = 2V2R5 - S², или 8 = R - 7«² -0,25Z². (2)

Рассчитанные по зависимости (2) значения граничных условий для применяемых размеров щеток [1] сведены в табл.1. На рис.3. приведены графики этих соотношений.

Радиальное смещение каждой i-той ворсины также определим из геометрии контакта как расстояние между точками 1 и 2 (рис.2). Тогда из условий пе- ресечения функций для координат точек 1 и 2 имеем соответственно:

(У1 = tg(90 + (pi)^;

I x\ + yX - R² = 0                  и

[У2 = tg(90 + 4>_t)x₂;

l У2 = ~R + 5,

R2

откуда : х_г = /----;— = R sin (0;;

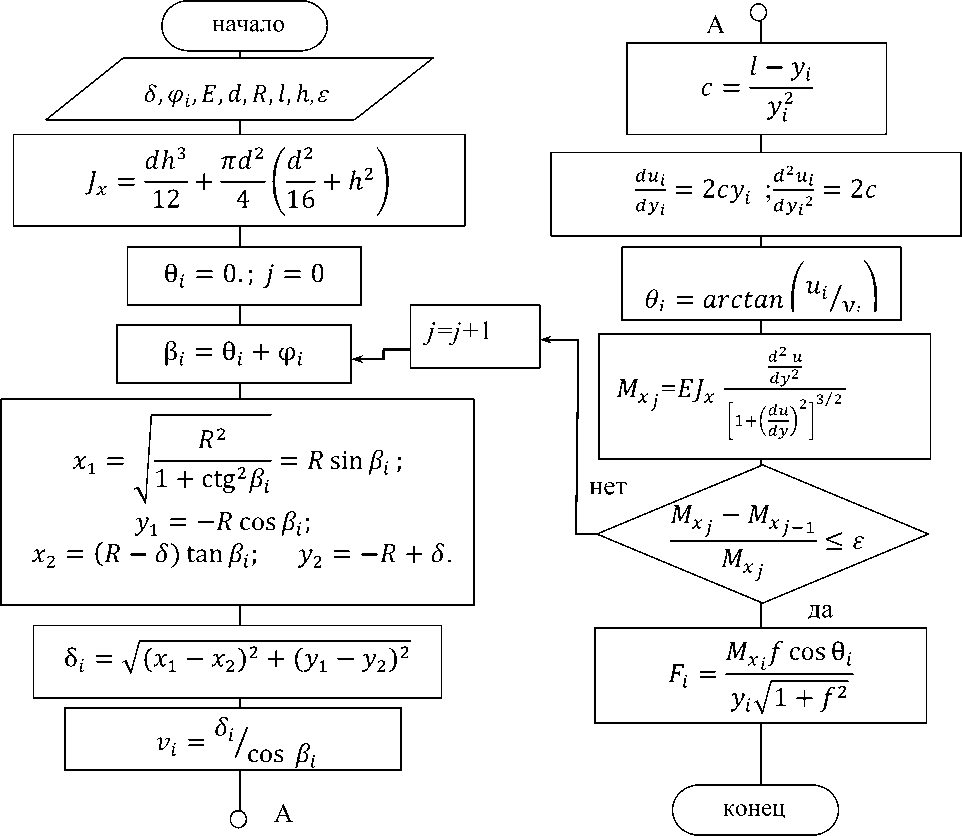
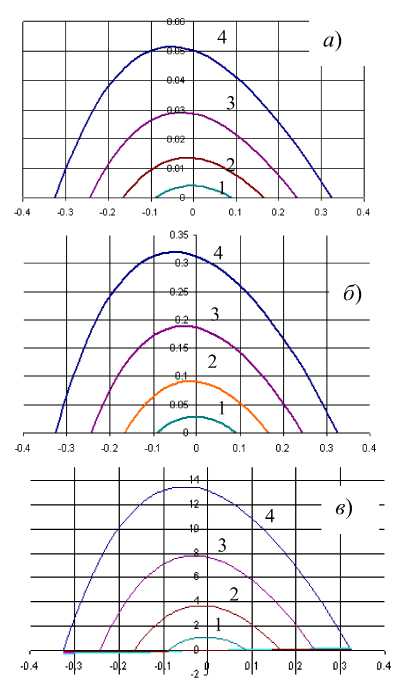
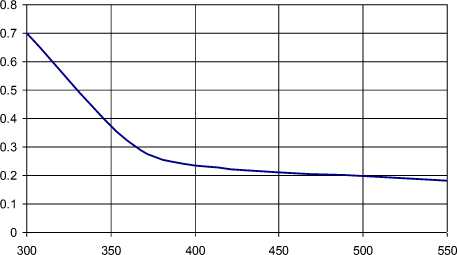
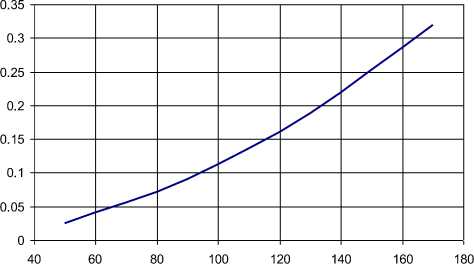
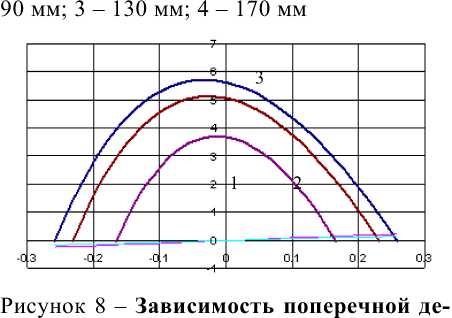
J 1 ^l+ctg2

У1 = —R cos (pi; x₂ = (R -5)tany₂ = — R + 5.

Таблица 1 – Зависимость глубины от ширины пятна контакта

Радиус щетки Ширина пятна касания	175	200	275	350	375	400	450	457,5
10,0	0,0714	0,0625	0,04546	0,03572	0,03333	0,03125	0,02778	0,02732
20,0	0,2859	0,2501	0,18188	0,14289	0,13336	0,12502	0,11112	0,1093
30,0	0,6440	0,5632	0,40940	0,32158	0,30012	0,28135	0,25007	0,24597
40,0	1,1466	1,0025	0,72824	0,5719	0,53371	0,50031	0,44466	0,43737
50,0	1,7949	1,5686	1,13872	0,894	0,83426	0,78201	0,69498	0,68357
60,0	2,5906	2,262	1,64126	1,28808	1,20193	1,12659	1,00111	0,98467
70,0	3,5357	3,0863	2,23637	1,7544	1,63691	1,53419	1,36318	1,34076
80,0	4,6327	4,0408	2,92464	2,29323	2,13944	2,00503	1,7813	1,75199
90,0	5,8846	5,1282	3,70680	2,90491	2,70979	2,53931	2,25565	2,21849
100,0	7,2949	6,3508	4,58365	3,58984	3,34828	3,1373	2,7864	2,74045
110,0	8,8675	7,7111	5,55613	4,34844	4,05526	3,79929	3,37376	3,31804
120,0	10,607	9,2121	6,62526	5,18121	4,83112	4,5256	4,01794	3,95149
130,0	12,519	10,857	7,79222	6,08867	5,67629	5,31658	4,71919	4,64103
140,0	14,609	12,650	9,05828	7,07144	6,59126	6,17263	5,47778	5,38691
150,0	16,886	14,595	10,42487	8,13014	7,57654	7,09416	6,29402	6,18941
160,0	19,356	16,696	11,89356	9,2655	8,6327	8,08164	7,1682	7,04884
170,0	22,029	18,961	13,46606	10,47828	9,76035	9,13557	8,10069	7,96552
180,0	24,916	21,394	15,14427	11,76931	10,96017	10,25649	9,09185	8,9398
190,0      90 -1	28,030  24,002  16,93024   13,13949 31,385  26,794  18,82623   14,5898 35    29,779  20,83470   16,12128 38,893  32,967  22,95834   17,73505 43,090  36,369  25,20008   19,43231 / 350 47,622    40    27,56314  21,21436 52,525  43,875  30,05103   23,08258 57,846  48,013  32,66758  25,03846 63,644  52,436  35,41703   27,0836 70    57171  3830399   292197 нок 3 - Зависимость глубины от ины пятна контакта l				12,23286	11,44498	10,14207	9,97207
200,00   80-U					13,57919	12,70167	11,25178	11,06271
210,0					15	14,0272	12,42144	12,21217
220,0 ________________________ 50					16,49616	15,42231	13,65152	13,4209
230,0    40 J—					18,06863	16,88774	14,94253	14,68937
240,0    30 J—					19,71842	18,42432	16,29503	16,01812
250,0    20 J—					21,44661	20,0329	17,70959	17,40768
260,0    10 1—					23,25435	21,71439	19,18682	18,85863
270,0					25,14289	23,46979	20,72736	20,37159
280,0					27,11352	25,30012	22,3319	21,94719
290,0    Рису					29,16767	27,20649	24,00117	23,58613
300,0    шир					31,30682	29,19008	25,73593	25,28911

Тогда искомое расстояние 5_t определим как радикал от разности квадратов координат точек 1 и 2

§i = 7(^Г-^2)^Г+7уГ-У2р.   (3)

Значения граничных условий 5[ для щеток диаметром D=550 мм приведены в табл. 2.

Таблица 2 – Граничные условия 5i для щеток диаметром D=550 мм

Ширина пятна контакта Фi		20		40		60		800			100			120		140	160	180
0.0		0.1818		0.728		1.6413		2.9246			4.5837			6.6253		9.0583	11.8936	15.1443
0.01		0.1681		0.7145		1.6276		2.9110			4.5701			6.6118		9.0450	11.8804	15.1313
0.02		0.1269		0.6733		1.5866		2.8702			4.5296			6.5716		9.0051	11.8409	15.0923
0.03		0.0582		0.6048		1.5183		2.8022			4.4620			6.5045		8.9386	11.7752	15.0274
0.04		0.0378		0.5089		1.4227		2.7071			4.3674			6.4106		8.8456	11.6832	14.9365
0.05				0.3856		1.2998		2.5848			4.2458			6.2900		8.7261	11.5649	14.8197
0.06				0.2349		1.1497		2.4353			4.0973			6.1426		8.5800	11.4204	14.6770
0.07				0.0570		0.9724		2.2589			3.9219			5.9685		8.4075	11.2497	14.5084
0.08						0.7679		2.0554			3.7197			5.7678		8.2086	11.0530	14.3141
0.09						0.5364		1.8250			3.4907			5.5405		7.9834	10.8301	14.0940
0.10						0.2779		1.5677			3.2349			5.2867		7.7319	10.5813	13.8482
0.11						0.0076		1.2835			2.9526			5.0065		7.4542	10.3065	13.5769
0.12								0.9727			2.6436			4.6999		7.1503	10.0060	13.2800
0.13								0.6352			2.3082			4.3670		6.8205	9.6796	12.9577
0.14								0.2712			1.9464			4.0080		6.4647	9.3276	12.6100
0.15								0.1192			1.5584			3.6228		6.0831	8.9501	12.2372
0.16											1.1442			3.2118		5.6757	8.5471	11.8391
0.17											0.7040			2.7749		5.2428	8.1187	11.4161
0.18											0.2378			2.3122		4.7844	7.6652	10.9682
0.19															1.8240	4.3006	7.1866	10.4955
0.20	16 14 12 10 8 6 4 2 0 n														1.3104	3.7916	6.6830	9.9981
										180 мм			4
0.21															0.7714	3.2575	6.1546	9.4763
0.22										160 мм					0.2073	2.6985	5.6016	8.9301
0.23										140 мм						2.1148	5.0241	8.3597
0.24										120 мм						1.5064	4.4222	7.7652
0.25																0.8735	3.7961	7.1468
										100 мм
0.26																0.2164	3.1460	6.5048
0.27																	2.4720	5.8391
										80 мм
0.28																	2.4720	5.1501
0.29										60 мм							1.7744	4.4379
0.30										40 мм							1.0532	3.7027
0.31		0        0.	05      0.		1        0.	15      0.	2       0.		25      0.	20 мм 3      0.		35      0.					0.3088	2.9446
0.32																		2.1639
0.33		Рисунок 4 – Изменение 8^ от угла Фi и ширины контакта																1.3607
0.34																		0.5353

График изменения 5^ в пределах угла перекрытия V (рис.2), где V = 2arctg , приведен на рис. 4.

Математическую модель процесса силового взаимодействия ворсины щетки при уже определенных граничных условиях будем строить исходя из допущений, что деформация (изгиб) происходит под действием сосредоточенной силы, приложенной к концу ворсины в зоне ее контакта с дорожным покрытием. Величину этой силы составляют сила трения Fтр и сила нормального взаимодействия N. При этом справедлив закон Кулоновского трения, так, что Fтр= f N, где f – коэффициент трения, величина которого перемена во времени и определяется условиями взаимодействия и состояния трущихся пар [2].

Дифференциальное уравнение равновесия нейтральной линии упругой ворсины имеет вид [3]:

d2 и

____dy²____ _ M_x l»®T'^{z = Eb} ,

где: E – модуль упругости первого рода; lx – момент инерции сечения вор

,      17 dh3 , ла2 fd2 , , 2 A сины (рис.1)Jx = — + —к—+гг .

1 /JX 12     4 ^16     J

Введем систему координат xiOiyi(Oi совпадает с точкой заделки ворсины 3), связанную с каждой ворсиной и повернутую на угол Ф i от инерциальной системы xOy

Рисунок 5 –Схема деформирования щеточного ворса: 1 – точка срыва; 2 – точка начала контакта; 3 – точка заделки ворса

Напряженно-деформированное состояние (НДС) каждой ворсины (рис.6) будет определяться граничными условиями, связанными с углом поворота Фi и прогибом, т.е. координатами конечного среза ворсины vi и. ui. Причем

^ ^— /COS ф1 . (5)

Определим (см. рис. 5), величину изгибающего момента M_x. ⁼ P_tX COS 0_t , где Pi = Jpp^i . Учитывая закон Кулоновского трения Pi = fNt , получим Pt = NiJT+p, или Pt = Ft^ . Окончательно для изгибающего момента имеем:

^M4⁼7^i^Fi^X.   (6)

^L J COS U(

Рисунок 5 –Схема изгиба ворсины

Аппроксимируем положение упругой линии каждой отдельной ворсины контакта конца ворсины с дорожным покрытием полиномом второго порядка xt = a + by + cyi , где а,b,c – коэффициенты, определяемые из граничных    условий    для    концов ны a = b = 0 . Тогда для функции центральной линии и ее производных получим:

2 du „    d2u „     mx

Xi = cy_t^;dy ~ ^^yi ^; ^ = 2c.   (7)

Введем граничные условия:

. ^.

Обозначим Pi ~ (Ti + 9i) и подставим граничные условия в уравнение упругой балки, получим для конечного среза ворсины u_t = cyp. Тогда для значения размерного коэффициента c получим формулу

^ y? ,               (8)

где: Ui = 7?sin0j ; 0i = arctan^/y?) .

Решение уравнения (4) с учетом (5   8) относительно граничных усло вий Ft при известной конечной деформации 8t и углового положения ворсины можем получить методом простых итераций при заданной точности расчета 8 . Алгоритм решения задачи представлен последовательностью, изображенной на рис. 6.

Результаты решения задачи приведены в виде графиков на рис.7 – 10.

Рисунок 6 – Алгоритм вычисления силы трения ворсины с дорожным покрытием

Из графиков следует, что характеристики силового взаимодействия ворса щетки зависят от величины сближения щетки с дорожным покрытием и от угла поворота щетки. Причем наибольших значений изгибающий момент достигает только лишь при прохождении ворсины больше середины пути контакта с дорожным покрытием.

Определим выражение для касательно силы контакта ворсины на основании (6) в виде: , тогда

Уг71+/ условием момента «срыва» (распрямления волокна за счет внутренней энергии упругой деформации), определяющим рабочий процесс, будет являться условие достижения значения этой силы величины силы трения в контакте, определяемой по условию Кулоновского трения коэффициентом трения, т.е.

M_xtf COS 0;

^Fi = ^J^

Разработанный алгоритм расчета сил взаимодействия ворса щеток с дорожным покрытием (рис.6) с учетом критерия (9) и математической модели процесса трения [1] может быть положен в основу методики оценки функционирования подметальных щеток коммунальных машин в различных ус-

ловиях их эксплуатации.

Рисунок 7 – Зависимость характеристик силового взаимодействия от угла поворота щетки: а) – тангенс угла контакта р; б) – изгибающий момент Mi, Нхмм;: в) – поперечная деформация волокна Vi ; ширина зоны контакта контакта:1 – 50 мм; 2 –

Рисунок 9 – Зависимость наибольшей величины изгибающего момента Mi , НXмм от диаметра щетки при ширине пятна контакта 90 мм

Рисунок 10 – Зависимость наибольшей величины изгибающего момента Mi , НXмм от и ширины пятна контакта

формация волокна Vi , мм от угла пово-