Математическое моделирование совмещенного процесса разливки и бокового прессования

Совмещенный процесс разливки и бокового прессования, представленный в работах [1, 2], предназначается для получения профилей, в том числе полых, способом комбинирования процесса разливки жидкого металла в контейнер, его кристаллизации, и прессования с боковым истечением металла. Данный способ, получивший свое развитие из работ [3, 4], позволяет получать длинномерные изделия на вертикальном прессовом оборудовании, исключая при этом образование пресс-остатка.

Основными параметрами, определяющими возможность протекания процесса прессования труб с боковым истечением металла в стабильных условиях, являются максимальные усилия прессования и выпрессовки пресс-остатка. Характер течения металла при боковом прессовании определяется рядом факторов, главными из которых являются: калибровка канала матрицы ( HМ , ω), положение и форма границ пластического очага деформации ( R1 , R , r1 , r , θ , β , γ ), режимы прессования ( νП1 , νП2 , λi ), условия трения на контактных поверхностях ( τS , μ), механические свойства исследуемого металла (σS ) и другие. Действия этих факторов определяют структуру моделируемой системы, свойства ее элементов и причинно-следственные связи, присущие системе и существенные для достижения цели моделирования [5].

Для упрощенного описания процесс условно делится на две зависимые стадии, определяемые объемом металла в контейнере. Так, движение большой пресс-шайбы до определенного момента времени, при котором объем металла становится равным критическому, с одновременным прессованием заготовки, обозначается как первый этап с максимальным усилием прессования P _max1 , затем движение малой пресс-шайбы, вызванное воздействием аккумулирующего устройства, и прессование оставшегося объема металла по горизонтальной оси с усилием P _max2 – как второй этап.

Следует отметить, что границами блоков зон пластической деформации при осесимметричном прессовании и выполнении условия несжимаемости являются сферы. Одной из характерных, влияющих на условия и результаты прессования, является зона, в которой металл на рассматриваемой стадии в истечении практически не участвует и образует объемы пластически не деформирующегося, находящегося в упругом состоянии металла. Так, для первого этапа упругая зона располагается на донной части контейнера, а на второй стадии застойная зона находится вблизи матрицы.

Расчетная схема процесса с геометрическими граничными условиями очага деформации при работе первого и второго этапов представлена на рис. 1 и 2 соответственно.

Уравнение баланса мощностей для случая прессования труб с боковым истечением металла и последующей выпрессовкой пресс-остатка включает в себя мощность сил деформирования с приложением усилия пресса P 1 или усилия аккумулирующего устройства P 2 , для первого и второго этапов соответственно, а также мощности формоизменения заготовки N Ф , мощность N _A , развиваемая максимальными касательными напряжениями на всех поверхностях разрывов скоростей S _A в заготовке, мощность сил контактного трения N _т .

Для математического описания совмещенного процесса и решения соответствующей задачи были приняты следующие основные допущения: деформируемый металл идеально пластичный (тS = оS,3з = const) и несжимаем; температура пластической горячей деформации в процессе прессования не изменяется (At = 0 ); деформация осесимметричная; силы контактного трения постоянны и не зависят от нормальных давлений (тк = р ■ тS); температурные напряжения и деформации, силы инерции и другие массовые силы пренебрежимо малы.

Путем преобразований уравнения баланса мощностей, с учетом всех переменных параметров получены зависимости для определения усилия прессования, возникающего на первом и втором этапах прессования труб с поперечно-боковым истечением металла и полной выпрессовкой пресс-остатка:

^P maxi = °= ^{п f 1} A + Р ^ V — ; ⁽¹⁾ 3 1 ⁴ J V _m

• ^ = 0|П ^f , C + ^ V N ^ , (2) 3 1 ⁴ ) ^V n2

где μ – коэффициент трения скольжения;

• V _ni , v _n2 - скорость прессования на первом и втором этапах соответственно; B , D – переменные параметры для определения мощности сил контактного трения для первого и второго этапов соответственно:

  

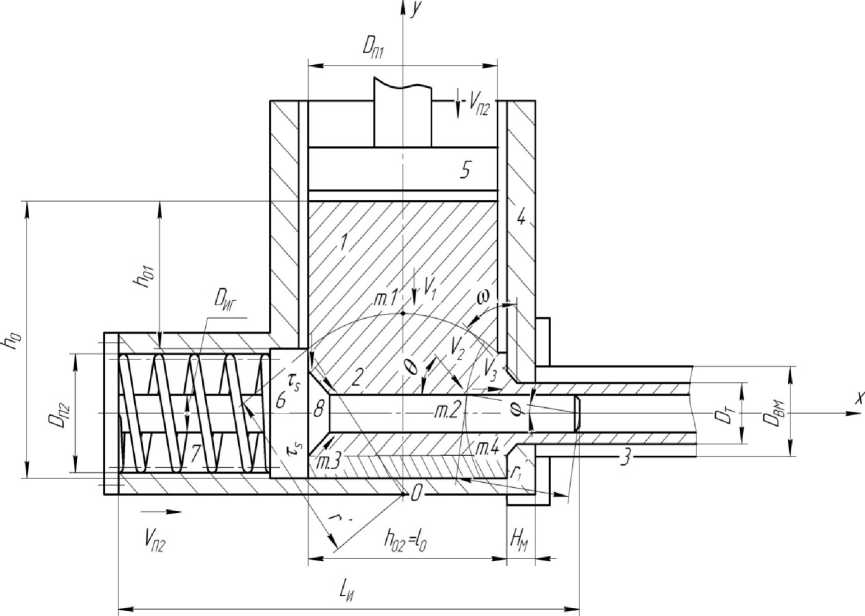
  Рис. 1. Расчетная схема процесса бокового прессования с геометрическими граничными условиями для первого этапа

  
  
  

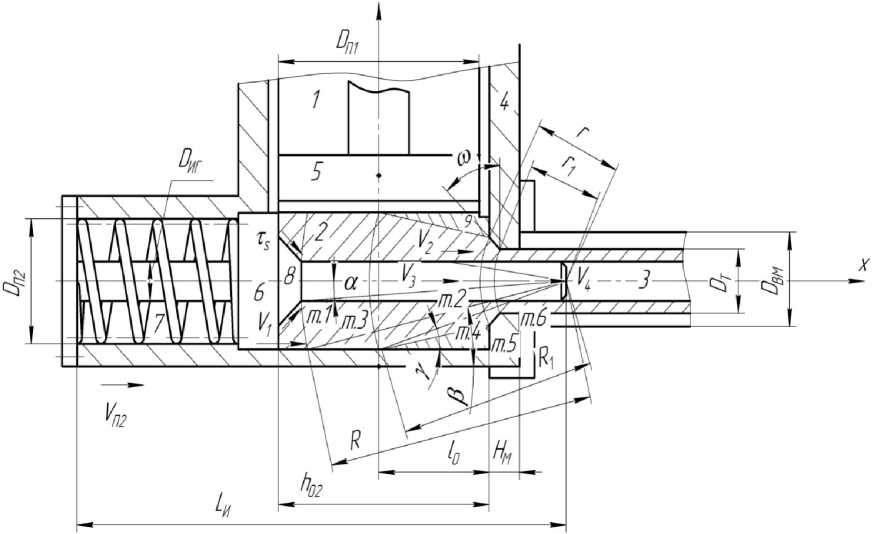
  Рис. 2. Расчетная схема процесса бокового прессования с геометрическими граничными условиями для второго этапа

  
  

  B = D K 1 ( h 02 + R ( 1 ^— cos Y ) ) +

  + ^2 ( D ВМ + D Т ) H М [ | }+ i d t ;         (3)

  D = D k₂ ( l о ⁺ R ( 1 ^— cosY ) ) +

  ⁺ ^2 ⁽ D ВМ ⁺ D T ) H М ^^  | ⁺ ID Т ;   ⁽⁴⁾

  
  

  A , C – переменные параметры для определения мощности, развиваемой максимальными касательными напряжениями на поверхностях разрывов скоростей S _д в заготовке для первого и второго

  
  

  этапов соответственно:

  
  

  II

  A =1l (Dк + Dзз )l|

  lv 1

  
  

  | l 0 H М ^r 1 |

  ⁺ K 2 ⁽ D 33 D ВМ ) l              || ;

  ( cos ф ) J

  
  
  
  

  + Z 2 ⁽ D 33

  
  

  L

  C = I 1 ( D К I^х

  —

  
  
  

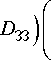
  R — R 1 cos ( y — в )

  
  

  +

  
  

  D ) | l 0 — H М - R — R 1 I ^ВМ ^ cose   cos ( в — Y ) J

  
  
  
  

  Таким образом, получена математическая мо-

  
  

  дель, основанная на использовании закономерностей теории пластических деформаций. Очевидным преимуществом этой математической модели для определения усилия при получении труб способом совмещения процесса разливки и бокового прессования является возможность сравнительно

  
  

  быстрого сопоставления результатов при разных режимах процесса.

  С целью оценки достоверности математической модели совмещенного процесса разливки – прессования труб с использованием устройства [1], обеспечивающего выпрессовку пресс-остатка, выполнен расчет значений максимального усилия прессования для двух этапов с использованием зависимостей (1) и (2).

  В таблице и на рис. 3 представлены результаты сравнения расчетных данных ( P _m ^р _a ^а _x ^сч ₁ , P _m ^р _a ^а _x ^сч ₂ ) и значений максимального усилия прессования труб ( P _m ^к. _a ^м _{x 1} , P _m ^к. _a ^м _{x 2} ) наружным диаметром 40 мм с толщиной стенки 10 мм из различных марок сталей с соответствующим сопротивлением горячей пластической деформации (σ_S), полученных с использованием программного продукта для моделирования и оптимизации процессов ОМД QForm 2D/3D.

  Значения максимального усилия прессования для первого и второго этапов, полученные при математическом моделировании процесса, показывают высокую сходимость с результатами, полученными при помощи компьютерного моделирования. Величина относительной ошибки результатов компьютерного и математического моделирования не превышает 13,56 %.

  Разработанная математическая модель совмещенного процесса разливки и бокового прессования труб с выпрессовкой пресс-остатка может быть использована для определения максимального значения усилия прессования и определения необходимого усилия аккумулирующего устройства.

  
  

Максимальное усилие прессования труб диаметром 40 мм с толщиной стенки 10 мм

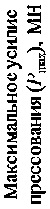
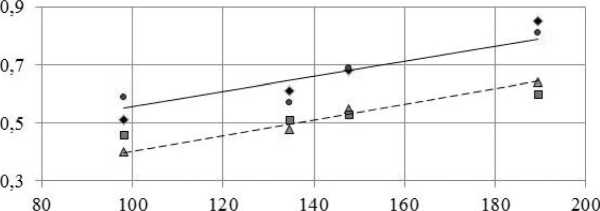
Сопротивление металла пластической деформации (os). МПА

— 1 -й этап: ♦ Компьютерное моделирование

• • Математическое моделирование

  - - 2-й этап: д Компьютерное моделирование

• ■ Математическое моделирование

Рис. 3. Расчетные и экспериментальные значения максимального усилия прессования труб диаметром 40 мм с толщиной стенки 10 мм

Ввиду того, что оценка достоверности математической модели совмещенного процесса разливки – прессования труб с использованием устройства [1], обеспечивающего выпрессовку пресс-остатка, выполнялась в сравнении с результатами компьютерного моделирования, которые принимались за истинное значение, требуется дальнейшее исследование процесса с использованием физической модели.