Математическое моделирование течения среды в сложных многоканальных системах

^ = 0, dx

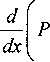
•² А т

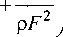
dmi _ dx

где т - массовый расход рабочего тела по каналу, кг/с;

Р - давление рабочего тела по каналу, Па;

i - энтальпия рабочего тела по каналу, Дж/кг;

р - плотность рабочего тела по каналу, кг/м3;

F - площадь поперечного сечения канала, м ;

II_W - периметр, м;

t_w - касательное напряжение трения на стенке;

q_w - тепловой поток из стенки к рабочему телу Вт/(м²К).

Система уравнений (1)-(3) дополняется замыкающими зависимостями по теплообмену, трению и теплофизическим свойствам:

• 2

=«(т;-г), tw =^—, а = a.^P,m,i^, р = р(Р, /), где а - коэффициент теплоотдачи, Вт/(м2-К);

Tw - температура стенки, К;

• Т - температура рабочего тела, К;

• ^ - коэффициент гидравлического сопротивления.

Для узла соединения каналов будем иметь соотношения, соответствующие закону сохранения массы (5), энергии (6), условию равенства давлений в узле и равенства энтальпий (7) на входе каналов, образующих узел, через которые происходит отвод теплоносителя:

^отДху =Zy)-^m/(x, =0) = 0,          (5)

^/йДху =Zy)zy(xy =ZV)-

• -^ т, (х, = 0) /, (х, = 0) = 0,           (6)

Pj ^ = Lj ) = Pi (x_t = О) = idem, i_t (x, = 0) = idem, (7) где индексы j - подводящий канал, i - отводящий канал.

Для местных сопротивлений считается, что их гидросопротивление зависит от расхода, давления и энтальпии в начальных сечениях, закон сопротивления принят квадратичным, на местном гидросопротивлении реализуется изоэнтальпийный процесс дросселирования, т.е. энтальпия потока до и после местного сопротивления неизменна, а температура изменяется ввиду падения давления. Без ущерба для общности будем считать, что местное сопротивление типа дроссельной шайбы является простым узлом, соединяющим у-й подводящий и i-й отводящий каналы. Уравнения, описывающие процессы на дроссельной шайбе, имеют следующий вид:

™AXJ = LA = ™I(X1 =0)’ ob^^^^U^0)’ pj к = чУрАх*=°)=^ Ар^А •    <8>

Для описания взаимодействия системы с окружающей средой требуется задание краевых условий на входе и выходе системы, т.е. для тех точек, где газ поступает в систему и выходит из нее (подводящие и отводящие устройства).

Для входного сечения л-го подводящего канала будем иметь:

Р™ = const, Lx = const, вх            > вх рвх - р„ (хп = °) = ^вх (рпЛ,9„).

В свою очередь, для ^-го отводящего канала: 4ых = COnSt,4(xi = 4)~4ых

Соотношения типа (9), (10) должны быть записаны для всех подводящих и отводящих магистралей, которых может быть в общем случае несколько.

Гидравлические характеристики местных и концевых сопротивлений примем квадратичными:

УР = К-^,                   (11)

Рр2

где К - коэффициент потерь.

Представленные уравнения и соотношения, записанные для каждого элемента системы, обра зуют замкнутую модель стационарного состояния системы.

Модель стационарного режима системы представляет собой нелинейную краевую задачу. Для ее решения необходимо построить сходящийся итерационный вычислительный процесс.

Применяя к уравнениям (1)-(3) процедуру квазилинеаризации [2] и дополняя их релаксационными членами [3], получаем:

P^'-P" dmn+i

(mn+x-m" dPn*x -------+---- t dx dP 2m 1 dpY dx pF2 p 8P > т2 1 др pF2 р 9Р

1 1 др pF² р dz

Я^П^т"^

-^- Ьт^пт^п+Х 8pF³J ^V

•Z7+1 -П

Г

л-т---- dx

.^df1 _ndin л-т--= m --+ a dx dx

^П_ад, (14)

где n - номер итерации; t - релаксационный параметр.

Для автоматизированного построения модели стационарного режима введем вектор состояния У, Г = \р^^х,...,Р^^х,т^^+х,...,т^пУ^,--^^ , (15) где N- число каналов в системе.

Тогда совокупность уравнений (12)—(14) может быть записана в следующей матричной форме:

—=0У+Ф ,                     (16)

dx где матрица 0 размером ЗУХЗУ и вектор Ф строятся из коэффициентов уравнений (12)—(14).

Таким образом, в © и Ф входят параметры только с л-й итерации, следовательно, система уравнений (16) является линейной относительно компонент вектора У.

Линеаризация краевых условий дает следующие соотношения:

- для узла соединения каналов: ^Т'р.рУТРГР =о)=о.

-Z^rk-oi-Z”"-rk=o)= tn»

-Z-^k-^f-Z^'-'k-o).

Шашкин В.Ю.

P^^L^P^^-idem, i^^x (x_z = О) = idem;

Алгоритм формирования матриц В, С, D состоит в следующем. Каждое из соотношений (17) -(20) можно представить в матричной форме:

- для местного сопротивления:

^х^Ь^ГЧ^У        (18)

рГЪ=ь;Ургх^=°У

В_}¥^п+1 (х, = 0) + CjYⁿ⁺¹ (х, =Ь^ = Dj,        (22)

где j - номер узла системы. Каждая из матриц Вj ,

Cj имеет 3N столбцов и М строк. Вектор Dj име

2Кт}

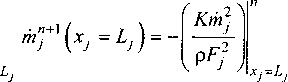
ет М строк, где М - число краевых условий, порождаемых данным элементом. Формирование этих матриц производится в соответствии со структурой соотношений (17)-(20).

Заполнение матриц В, С, D из (21) производится по блочному принципу подобно схеме:

- для входного подводящего канала:

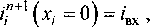
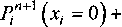
^2^ . Р^2

Кт^Л

P^J

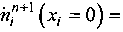
- для выходного отводящего канала:

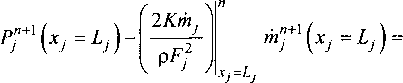
Таким образом, после линеаризации совокупность краевых условий для циркуляционной многоканальной системы, состоящей из указанных выше элементов, может быть представлена в следующей матричной форме:

BⁿY^nti (х, = 0) + c"Y^n+v (x_f = L^ = Dⁿ,        (21)

где В и С - матрицы размерностью 3N^3N , a D - вектор-столбец, содержащий 3N элементов. Матрицы В, С, D формируются на основе соотношений (17)-(20) с учетом конкретной заданной структуры системы, стационарное состояние которой требуется определить.

Решение краевой задачи (16), (21) до достижения сходимости итерационного процесса даст искомый набор параметров (давление, массовый расход, энтальпия) стационарного состояния системы. Данное решение получено на основе метода прогонки (сведения к задаче Коши).

Матрицы В, С, D содержат всю информацию о структуре системы. Таким образом, автоматизированное построение вычислительной модели стационарного состояния сводится к формированию указанных матриц по специальному алгоритму.

	в,		с,
в =	Bj	, с=	cj	, D =
	В„		С„		Dt

где к - число узлов в системе.

Для реализации метода прогонки задача (16), (21) сведена к задаче:

BⁿY^n+x (х, = 0) + c”Y^n+x (х, =L,) = Dⁿ .

Для             этого у _ I ри+1         ™л+1 7л+1 F г                   ,тх ,...,mN ,ix           | няется еще одной компонентой уз^ь

вектор допол- система

дифференциальных уравнений (16) - уравнением ^dl±k = 0, матрица А - нулевой строкой, столб-dx цом Ф и элементом #3n+i, зн+i = 0, а краевые условия дополняются условием узн+iteN+i = 0) = 1.

Методом прогонки (сведением к задаче Коши) находится решение краевой задачи (23).

Разработан алгоритм, на основе которого создана прикладная программа, позволяющая определять параметры (величину массового расхода, энтальпию среды в каналах, направление ее течения, давление в каналах) стационарного состояния системы каналов произвольной заданной структуры и оперативно исследовать как всю систему в целом, так и отдельные ее подсистемы.

Разработаны схемы моделирования течения теплоносителя по сложной многоканальной системе (порядок нумерации каналов и узлов многоканальной системы). При этом количество каналов, входящих в систему, может превышать 1000, а схема их соединения быть любой сложности.

Модель может использоваться для расчета и анализа энергетической эффективности поверхностей нагрева при сложной многоканальной схеме течения теплоносителя, например, насадки регене-

ративного теплообменного аппарата, а также для моделирования процессов в пористом теле.