Математическое моделирование технических систем в нормальной форме пространства состояний

выходной переменной (вложенная структура модели с обратными связями по переменным состояния); введением переменных состояния методом понижения порядка (вложенная структура модели с местными обратными связями по выходу) и 2 метода формирования выходной координаты системы: пропорционально одной из координат системы и в виде взвешенной суммы координат состояния (рис. 1). В результате образуется система из 8 модификаций математических моделей в нормальной форме ПС – 4 с прямой причинноследственной связью и 4 – с обратной причинно-следственной связью.

Рис. 1. Методы формирования моделей систем управления в нормальной форме пространства состояний

Суть предлагаемых методов математического описания системы n-го порядка nm

Z a i x ⁽ i ⁾⁽ t ) = £ j ⁽ j ⁾⁽ t ) i = 0             j = 0

с выходной x и входной y координатами, коэффициентами характеристического полинома ai и оператора входного воздействия bj в нормальной форме пространства состояний с прямой причинно-следственной связью первой модификации [1, 2], состоит в том, что переменные состояния vv в моделях ПС

полюсов и m нулей

V ^{( 1 )}( t ) = AV ( t ) + By ( t ) ; x ( t ) = CV ( t ) + dy ( t )

* m *     m - 1         *     *

„ , , _ b m s  + b m — i s    + ... + b i s + b o

W ⁽ s ) n . *      n - 1 .      . * . *

s + ^ n - 1 s    + ... + a i s + a o

,

вводят, начиная с n -oй фазовой переменной в соответствии с выражением

матрицы в математических моделях НФПС с прямой причинно-следственной связью могут быть представлены в виде следующих четырёх модификаций

x ^{( n v} ) ( t ) , v e ( m , n ] ;

,    .       m - v

x ^{( n - v} ) ( t ) - 2 W ( t ) , ⁱ = 0

^v< 0, m ^] ;

^ x ^{( n} ) ( t ) + X o y ( t ) ,        v = 0,

*

^{- a}n - 1

*

a n - 2 ••• ^{- a}1

.

.

.

A =

.

.

.

значения коэффициентов λ i вычисляют по рекуррентным формулам

..

.

..

.

.

.

.

.

.

.

X i =

* b_i ,

i = m ;

C =

;

* ^m *

bi     2 Xjan+i- j, j=i+1

i = m - 1,0,

*

^{- a}n - 1

*

a n - 2 ■■■ ^{- a}1

.

.

.

а матрицы A, B, C и коэффициент d задают в виде

A =

.

.

.

..

.

..

.

.

.

.

-an-1 - an-2 ...- a2 - a*

1        0    ...    0     00

0        1     ...    0     00

...           ...... ...       ......

0       0    ...    1     00

0        0     ...    0      10

’ X0 1

X1

B =

λ m -1 λ _m

0 C = [ 0 0 ... 1 ]

;                                                          ;

d =

^X m ,

I0,

при m = n ; при m <  n .

Здесь a* = a i [a n , i = 0, n ; b = b j/an , ^j = ⁰ m , В общем случае для объектов исследования, передаточные функции которых содержат n

.

.

.

*

.

*

.

..

..

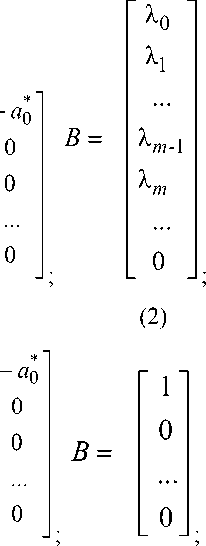
... C 0 ] _;

C = [ C n - 1

C n - 2

A =

..

.

...

C = [ 0

A =

..

.

C = [ X n - 1

...

^X n - 2

...

;

0...0

0 ... 0

0...0

0... 1

.........

;

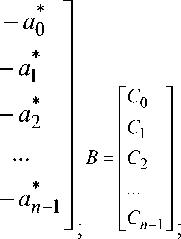
0...0

0 ... 0

0...0

0... 1

.........

.

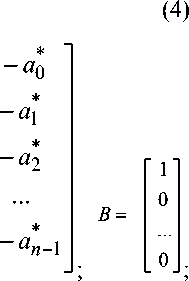
X0]

Коэффициенты в предлагаемых математических моделях определяются следующими выражениями:

z , = b i - t jn _{+ l} - j, i = \T n j = i + 1 ;

*             ,*       * *

C n = b n C i = b i    b n a i ,    ¹ = °’ ^{n 1}

,                                                                                        .

Для моделей с обратной   причинно следственной связью

• V * ^{( 1 )} = a * V * + в * У, ;

x = С* V* + dy система (1) является сопряжённой

• К^{(1 )} = A ^Т V * + С ^Т у. ;

• x = B ^Т V * + dy .

Поэтому матрицы в этих моделях задаются формулами

• A * = A ^Т B * = C ^Т C * = B ^Т •

При моделировании сложных объектов машиностроения, состоящих из разнородных элементов’ к отдельным частям системы предъявляются противоречивые требования, что обуславливает необходимость использования при исследовании этих систем комбинированных форм пространства состояний. Так, при исследовании управляемых приводов авиационных тренажёров, станков, центрифуг и многих других объектов, необходимо анализировать поведение механических координат: перемещений, скоростей, ускорений, градиентов ускорений (линейных или угловых), что может быть эффективно проведено на моделях первой модификации (2). Для управляющей части при этом возникает необходимость независимого формирования, вариации и анализа отдельных компонент, пропорциональных производным или интегралам ошибки в системе. Поэтому управляющую часть замкнутой системы целесообразно моделировать на базе моделей второй модификации (3). Моделирование систем с внутренними обратными связями по выходной координате рационально на базе моделей (4), (5).

В качестве примера приведём математическую модель замкнутой системы следящего электропривода постоянного тока, матрицы которой имеют следующую структуру

	- a 2	- а к	- а к	°	°	- 1		Г т 1
	1	°	°	°	°	°		о °
A =	°	1	°	°	°	°	B =	°
	C 2	C 1	C ° -	а г	- а 1	- а ° - C 3		C 3
	°	°	°	1	°	°		°
	. °	°	°	°	1	° .		_ ° _
			С =	[ 0	° °(	) ° 1 ]	;

Первые три строчки матрицы системы задают структуру и параметры регулятора, а последние три строчки - структуру и параметры объекта управления (машины постоянного тока с вентильным преобразователем). При этом первая часть матрицы A представлена в форме модели второй, а вторая - первой модификации ПС, что позволяет с одной стороны эффективно исследовать структуру формирования управляющего сигнала, а вторая определить характер изменения угла поворота, скорости и ускорения в системе (рис. 2).

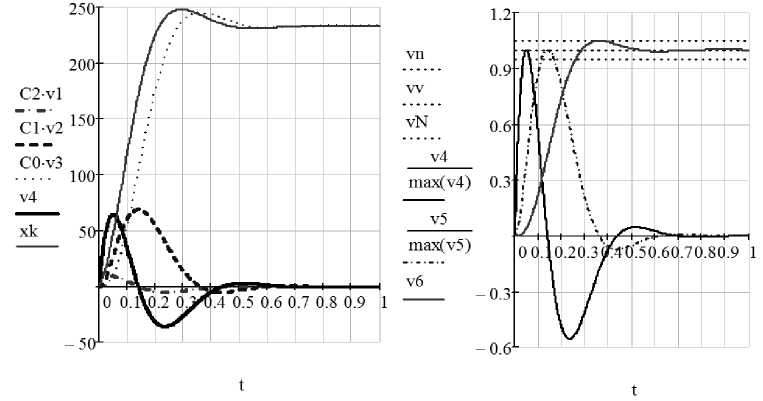
Рис. 2. Характер изменения переменных состояния в модели электропривода

Результаты исследования следящего электропривода постоянного тока мощностью 0,17 кВт в среде Mathcad (рис. 2) отражают соотношения между составляющими управляющего сигнала, пропорциональных ошибке и её производным. Наименьшее значение имеют составляющие пропорциональные третьей и второй производным. При C 3 =0 перерегулирование увеличивается незначительно с σ=4,981% до σ=5,223%, при C 2 =0 возрастает до σ=6,830%, при C 2 =C 3 =0 повышается до значения σ=7,128%. Изменение настроек регулятора по первой производной и по ошибке системы существенно изменяет характер переходных процессов, увеличивая колебательность и более чем в пять раз перерегулирование следящего электропривода.

Выводы: отличительная особенность предлагаемой системы математических моделей в нормальной форме пространства состояний с прямой причинно-следственной связью состоит в том, что каждая последующая координата состояний формируется на основании предыдущей, что обеспечивает единство методологических принципов и повышение эффективности при исследовании, анализе и синтезе систем управления по моделям «Вход – выход» и «Вход – состояние – выход».