Математическое моделирование технологического процесса очистки древесины в корообдирочном барабане

Очистка от коры является важным этапом подготовки древесного сырья к его дальнейшей переработке. В зависимости от условий производства окорка может осуществляться различными способами [1-8 и др.].

В целлюлозно-бумажном и ряде других производств широкое распространение получил способ групповой очистки древесного сырья с использованием корообдирочных барабанов. Такой способ окорки является весьма энергоемким, что предопределяет как существование проблемы совершенствования этого технологического процесса, так и актуальность решения данной проблемы с учетом современных требований. В целом проблема совершенствования рассматриваемого технологического процесса очистки древесины является достаточно сложной, включающей в себя ряд задач, которые требуют для своего решения проведения комплексных исследований.

Исследование очистки древесины в корообдирочных барабанах, проводимое в данной работе, направлено на поиск путей снижения энергоемкости окорки и решение проблемы совершенствования этого процесса.

Исследованию различных аспектов данной проблемы посвящен ряд работ, обзор которых приведен, например, в [9]. Очистка древесины в корообдирочном барабане осуществляется за счет механического взаимодействия бревен друг с другом и с элементами корпуса барабана в процессе его вращения вокруг продольной оси. При вращении барабана бревна, опирающиеся друг на друга и на поверхность барабана, поднимаются вверх, затем, достигнув некоторой высоты, перемещаются вниз, соударяясь друг с другом и с корпусом барабана. В результате происходящего динамического взаимодействия происходит отделение коры. При этом эффективность процесса окорки зависит от соотношения размеров барабана и обрабатываемого сырья, влажности и температуры, от скорости вращения, степени заполнения барабана и других факторов. Очевидно, учет этих факторов необходим при разработке рекомендаций по совершенствованию технологии окорки. Изучение степени влияния этих факторов на характеристики технологического процесса, безусловно, требует проведения натурных испытаний. Однако по техническим и экономическим условиям проведение таких испытаний возможно в ограниченном диапазоне конструктивных и технологических характеристик. В этой связи становится не только целесообразным, но и необходимым применение соответствующих математических моделей и современной вычислительной техники. Анализ многочисленных публикаций по проблеме окорки [1, 2, 5, 7 и др.] показал, что известные математические модели применимы к задачам узкого класса и недостаточно эффективны, в связи с чем все более актуальными становятся их совершенствование и разработка новых моделей.

В то же время недостаточно изучены перспективы применения современных численных методов при математическом моделировании динамического взаимодействия подвергаемых очистке балансов друг с другом и с корпусом корообдирочного барабана. Вследствие своей относительной новизны эти методы еще не нашли широкого применения в тех областях, где они могли бы оказаться достаточно эффективными.

К таким методам относится метод дискретных элементов, первоначально предложенный как инструмент решения задач механики горных пород [10]. В простейших моделях дискретные элементы рассматривались как абсолютно жесткие тела, связанные в точках контакта воображаемыми бесконечно малыми деформируемыми элементами. В современных подходах материал контактирующих тел считается деформируемым, что предполагает использование метода конечных элементов. Появляющаяся в этой связи задача эквивалентна задаче динамики системы деформируемых тел с односторонними контактами, при ее решении на каждом шаге по времени могут быть использованы различные подходы [11].

В данной работе при построении математической модели динамического взаимодействия балансов использованы уравнения движения, записанные в форме уравнений статического равновесия, в которых силы динамического взаимодействия определены согласно принципу Даламбера. Используется также гипотеза Фойгта о пропорциональности силы сопротивления скорости деформирования. В рассматриваемой физической модели с механическими соударениями необходимо учитывать условия отсутствия взаимопроникновения в области контакта тел друг с другом и с корпусом корообдирочного барабана, для чего применен изложенный в работе [12] подход.

Теоретические аспекты моделирования систем с механическими соударениями и решения ряда задач с применением аналитических и численных методов рассмотрены, например, в работе [11]. Как известно, аналитические решения могут быть получены для ограниченного класса задач. Применительно к моделированию рассматриваемого технологического процесса целесообразно применение численных методов, что объясняется сложностью объекта исследования.

С учетом особенностей прикладной задачи при построении математической модели целесообразно использование названного выше метода дискретных элементов и метода конечных разностей в сочетании с методом конечных элементов. Необходимость учета условий контактного взаимодействия деформируемых тел при соударениях существенно усложняет задачу в вычислительном отношении. Изучение данного вопроса показало, что достаточно эффективная математическая модель для решения задач рассматриваемого класса может быть построена с использованием и адаптацией алгоритмов, в которых исходная проблема формулируется как линейная задача дополнительности [12]. В этом случае модель позволяет прогнозировать траекторию, скорость и ускорение движения каждого отдельно взятого бревна, число соударений, величину и продолжительность действия сил динамического взаимодействия бревен друг с другом и с корпусом барабана [13].

Рассмотрим модельный пример. Тело массой m = 50 кг соударяется с девятью такими же телами (рис. 1). В начальный момент времени зазоры Z i между телами i = 1, 2, „., 9 и корпусом барабана равны нулю. Зазор Z 10 = 2 м. Коэффициент жесткости, определяющий деформируемость контактирующих тел, может быть определен экспериментально и в данной работе принят равным 20000 кН/м. Сила сопротивления движению при соударении и деформировании тел, как отмечено выше, пропорциональна скорости, причем коэффициент пропорциональности к , определяющий рассеяние энергии, принят равным для двух вариантов расчета: 5000 кг/с и 10000 кг/с. Требуется определить величину и продолжительность действия сил в контактах Z 10 , Z 9 ,..., Z 1 .

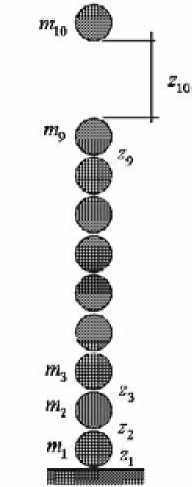
Рис. 1. Система десяти тел с зазорами

Математическое моделирование технологического процесса очистки древесины в корообдирочном барабане

Результаты расчета по представленной методике приведены на рисунках 2 и 3. Отсчет времени начинается от момента соударения тел 10 и 9. Принято следующее правило знаков: сила контактного взаимодействия положительна, если вызывает сжатие тел.

Согласно результатам расчета с увеличением коэффициента k максимум силы при соударении тел 10 и 9 уменьшается от 87 кН до 82 кН.

С развитием процесса соударения максимумы сил контактного взаимодействия тел 10 и 9, 9 и 8 и т. д. также уменьшаются, однако увеличивается продолжительность этого взаимодействия. Продолжительность процесса соударения не зависит от k .

Технологический результат действия силы контактного взаимодействия в данном случае зависит не только от величины силы, но и от продолжительности ее действия. Однако если величина силы достаточно мала, отделение коры не будет иметь места.

Предлагаемая модель, построенная с использованием метода дискретных элементов в сочетании с методом конечных элементов и методом конечных разностей, позволяет находить решения достаточно широкого класса задач, связанных с формированием технологических процессов и обоснованием параметров оборудования для очистки древесины от коры.

Результаты расчета по представленной методике могут быть использованы при обосновании рациональной степени загрузки корообдирочного барабана, скорости вращения и его диаметра.

Для уточнения практических рекомендаций необходим учет не только нормальных, но и касательных сил контактного взаимодействия. Соответствующие расчеты также могут быть выполнены по представленной методике

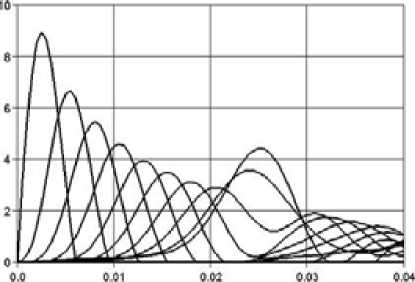
Рис. 2. Зависимость сил в контактах Z₁₀, Z₉,…, Z₁ (указаны в ньютонах, по оси ординат) от времени (в секундах, по оси абсцисс), k = 5000 кг/с

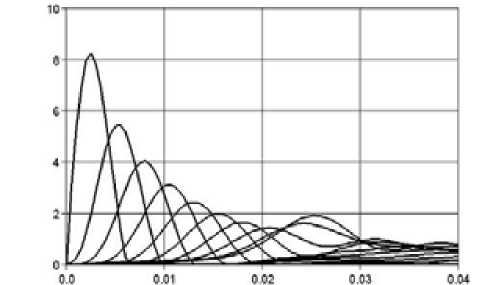
Рис. 3. Зависимость сил в контактах Z₁₀, Z₉,…, Z₁ (указаны в ньютонах, по оси ординат) от времени (в секундах, по оси абсцисс), k = 10000 кг/с