Математическое моделирование температурного поля при контактной точечной сварке

Математическое моделирование изменения температурного поля при контактной точечной сварке (КТС) является исходным условием разработки математических моделей других термодеформационных процессов. В частности, аналитический анализ термо деформационных процессов возможен только в случае, если математическая модель температурного поля удовлетворяет, по крайней мере, двум условиям: описывается непрерывной функцией и в достаточной степени точно отражает динамику его изменения в процессе формирования соединения. При этом известные аналитические методы расчетов температуры при КТС, как показано в работе [1], не достаточно точны, а в наиболее точных методиках расчетов, в основе которых лежит решение дифференциальных уравнений распределения потенциалов и теплопроводности в зоне сварки [2], результаты расчетов представляют собой дискретные значения температуры.

Поэтому для анализа термодеформационных процессов при КТС деталей из легких сплавов электродами со сферической рабочей поверхностью был разработан экспериментально-расчетный метод оценки температуры в зоне сварки [3], основанный на монотонности и подобии [4] изменения параметров термодеформационных при точечной сварке. При сварке электродами с плоской рабочей поверхностью и при КТС с обжатием периферийной зоны соединения изменение температуры в зоне сварки существенно отличается от ее изменения при сварке электродами со сферической рабочей поверхностью [5]. Поэтому метод оценки теплового состояния зоны сварки существенно усовершенствован. Суть его заключается в следующем.

Температурное поле при конкретных условиях КТС можно описать функциями, аппроксимированными по экспериментально определенным характерным пространственно-временным точкам.

Цля нахождения вида аппроксимирующих функций (рис. 1), которые с достаточной точностью отображали бы изменение температуры в плоскости оси электродов по координатам гиг для конкретного процесса сварки в любой его момент экспериментально можно определить значение температуры, по крайней мере, в четырех характерных местах зоны сварки: по координате z (рис. 1, а) - температуру Т_э в контакте электрод-деталь (2 точки); температуру плавления Т_ПЛ по координатам границы ядра (2 точки); по координате г (рис. 1, б) - температуру плавления Т_ПЛ по координатам границы ядра (2 точки); температуру Т_П внешнего контура уплотняющего пояска (2 точки).

Установлено, что изменение температуры по координатам гиг, показанное на рис. 3, 4, удовлетворительно описывается функцией вида y = b • e^ax )= b• exp[ -(ax2)] , (1) где x - произвольная переменная; а и Ъ - коэффициенты, которые можно определять по имеющимся экспериментальным значениям температуры.

Рис. 1. Характерные значения температуры в плоскости оси электродов по координатам z ( я ) и г (б), которые при КТС в любой момент можно определить экспериментально

Из анализа результатов исследований процесса КТС можно сделать допущение, что изменение температуры по времени на стадии нагрева в любой точке зоны сварки подобно ее изменению в контакте электрод-деталь (рис. 2). При этом общеизвестно, что температура в контакте электрод-деталь при сварке на стадии нагрева возрастает монотонно (рис. 2, а).

При точечной сварке измерение изменения температуры по времени в контакте деталь-деталь и свариваемых деталях затруднено малыми размерами и закрытым характером зоны формирования соединения, а также бы- стротечностью процесса КТС. Вместе с тем, о температуре в центре контакта деталь-деталь можно судить по ее изменению в трех точках, в которых температуру можно определить экспериментально (рис. 2, б): в начале процесса она равна температуре окружающей среды (при t = 0 - Т( = 0); в момент начала плавления tHn - температуре плавления Тпл металла (при t = t - Tt = Тпл); в момент выключения сварочного тока tCB она достигает максимального Тм значения (при t = t - Tt = Тм).

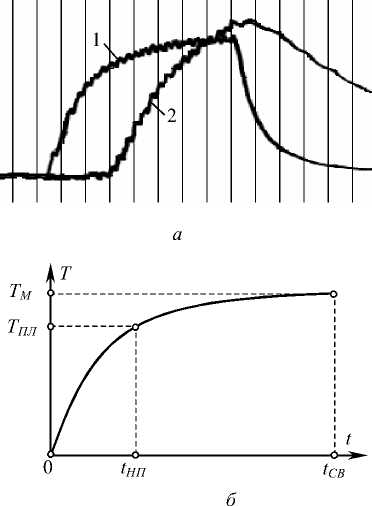
Рис. 2. Осциллограмма (а) и схема (б) температуры в контакте электрод-деталь при КТС:

АМг6, 1,5 + 1,5 мм; /_СВ= 27 кА; Л _b 6,6 кН;

t = 0,08 с; 1 - ток, 2 - температура

Установлено, что аппроксимировать изменение температуры на стадии нагрева как с точки зрения точности расчетов, так и компактности расчетной зависимости, наиболее рационально степенной зависимостью следующего вида:

Т_х = н (ШнП >^с, (2) где и и с - коэффициенты, которые подлежат идентификации.

Разработка математической модели температурного поля по расчетно-экспериментальному методу, в сущности, сводится к определению и математическому описанию взаимосвязей аппроксимирующих функций (1), описывающих изменение температуры по координатам z и г, и функции (2), описывающей ее изменение по времени t.

Значения коэффициентов Ъ и а в зависимости (1) применительно к конкретному процессу сварки можно найти по значениям температуры в характерных точках. Для этого предварительно для момента времени t преобразовав зависимость (1) к виду

^T Z. = b t exp [ ^-( a Zt z ) ² ] , (3) составим систему уравнений (при z = h_яt/2 температура С ^Т_н , ^апр^{и z s Т},- ^ТЛ

^Т пл = ^b . exp [ ^-( a z, h я, /² ) ^{2 ]}

^T 3 t = ^b exp [ ^-( a Z, s ) ² ]

где h - высота ядра расплавленного металла; Т_Э - температура на поверхности деталей под электродами; Т_пл - температура плавления металла; s - толщина деталей.

Решив эту систему уравнений, находим значения коэффициентов Ъt и aZt по формуле bt = Тпле^Р(aA, /2)2, azt = ^ln (Тпл Тэ.)/(s2 —(hя, /2)2) , подставив которые в (3), получим зависимость для расчета температуры TZt на оси электродов в точке с координатой z в момент времени t процесса КТС. После преобразований она будет иметь следующий вид:

T zt = Т пл exp { a Z, [ ( h я, /2) 2 — z ² ]} .         (4)

Эта зависимость имеет хорошую сходимость результатов при расчете изменения температуры по координате z с результатами расчетов температуры численными методами (рис. 3). Это, например, подтверждается изменением температуры по оси электродов в момент выключения сварочного тока при сварке сплава АМг6 (рис. 3, а), рассчитанное по формуле (4) и методом конечных разностей в работе [6].

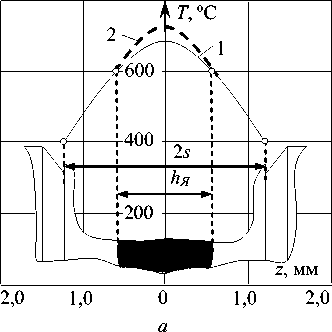
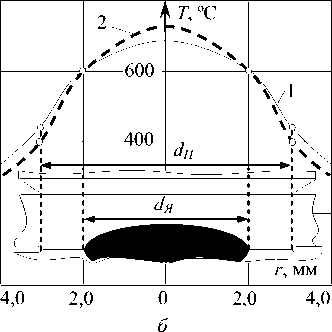
Рис. 3. Изменение температуры по оси электродов (а) и в плоскости контакта деталь-деталь (б) в момент окончания нагрева: АМг6, 1,2+ 1,2 мм, t_CB = 0,08 с; 1 - рассчитанное методом конечных разностей; 2 - рассчитанное по зависимостям (4) и (7)

Для расчета в момент времени t изменения температуры T_t по координате г зависимость (1) преобразуем к виду

T = ^{ь ;} exp [ ^-( a rt r ) ^{2 ]} ■              (5)

Определить коэффициенты Ъ * и а можно аналогично тому, как определяли коэффициенты Ъ_t и a_Zt в зависимости (3), по значениям температуры T_гt (рис. 2, б) в характерных точках (при г - dJ2 - T_t - T_п, при г - dJ2 - T_t - T_пл и при г ⁰ А Гл

Поскольку в точке с координатами г = Оиz = 0 температура имеет максимальное значение T_M, то из зависимостей (4) и (5) можно записать следующее соотношение:

Тплexp{ aX [(hя,/2)2-02]}—b exp[-(art • 0)2], из которого можно определить коэффициент Ъ * для данных условий сварки по формуле b = Тпл exp[(az,hя,/2)2 ] , а зависимость для расчета температуры по координате г записать следующим образом:

T rt = ^Т пл exp ^[ a В ( h я, /² ) ² — a rt ^{r 2} ] ■

Поскольку на границе ядра расплавленного металла при г - dЯt/2 значение T - T , то из этой зависимости можно определить значение коэффициента а, которое будет равно art = azt (hя, Id я,) ■                     (6)

Тогда зависимость для расчета изменения температуры по координате г в окончательном варианте имеет следующий вид:

T rt = Т пл exp [ a Z, ( h я, /2 ) 2 — ( h я, Id я, ) 2 r ² ] .    (7)

Изменение температуры по координате г в момент выключения сварочного тока, рассчитанное по зависимости (7), также хорошо согласуется с результатами расчетов методом конечных разностей (рис. 3, б).

Для расчетов изменения температуры в любой точке плоскости z-г зависимости (4) и (7) следует объединить. Это можно сделать, если учесть, что температурное поле неразрывно, а температура на оси электродов T_Zt при любом значении координаты z является максимальным значением температуры Т_М по координате г, т. е. при г = 0 значение T_Zt = Т_М. Из зависимостей (4) и (7) это соотношение температур по координатам z и г можно записать в виде выражения

^Т пл exp | a Z, ^[( ^h я, /² ) 2 ^{- z 2 ]}= ^Т пл exp ^[ a Z, ( ^h я, /² ) ^{2 -}( ^h я, Id я, ) ² • ⁰2 ^] , после преобразований которого получаем зависимость для расчета температуры в момент времени t в любой точке плоскости z-г в пределах зоны сварки, имеющую следующий вид:

T z , r , t = Т пл exp { a Z, [ ( h я, /² ) 2 — z ² — ( h я,/dя, ) 2 r ² ] } . (8)

Характер температурного поля по координатам z и г, рассчитанный по зависимости (8) для момента выключения тока, т. е. при t - t , показан на рис. 4.

Для анализа термодеформационных процессов в зоне сварки необходимо математически описать изменение температуры не только по координатам, но и по времени. Для этого зависимость (8) необходимо функционально связать с зависимостью (2).

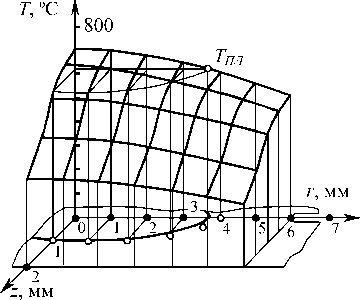
Рис. 4. Температурное поле для условий сварки АМгб, 2 + 2 мм, I_CB = 45 кА, F_CB - 8,5 кН, t_CB = 0,1 с (точками обозначены размеры ядра по макрошлифу)

Определить значения коэффициентов и и с в зависимости (2) можно, исходя из следующего. B момент времени t начала плавления металла температура в точке с координатами z = Ои г = 0 равна Т^, т. е. при t = t_Hn — T_t = = Т_пл. B момент же окончания импульса тока t температура в контакте деталь-деталь достигает максимальных значений Т_М, т. е. при t = t - T₍ = Т_М. Это позволяет составить систему уравнений

^ м ^{— и ( ,}свАяп )

,

^Тпл ^{— и ( ,}яп ЬнП )

после решения которой и находим искомые коэффициенты и и с:

n ^{— Т} пл , ^{с — ( а} zt ^ИЯ1 /²⁾ /ln ^{( ,}св ^нп ) .

Тогда зависимость для расчета изменения температуры в центре контакта деталь-деталь можно записать в виде

Т t = Т пл (Ф пп ) ^{С ,}                 (9)

где с - коэффициент, определяемый по конечной высоте ядра Ля при t = t и равный с — (аz Ия/2) /lnАсдАяп), aZ - значение коэффициента aZt, определяемого по зависимости (4) так же по конечной высоте ядра Ля и максимальной температуре TЭ в контакте электрод-деталь:

a z — \ ln ( Т пл Т )/ [ » ² - ( h я /2 ) 2 ] .

Характер изменения температуры в центре свариваемого контакта, рассчитанный по зависимости (9) для различных условий сварки, показан на рис. 5. Такое изменение температуры вполне согласуется с данными, полученными как экспериментально, так и расчетами методом конечных разностей.

Выразим значение Тпл металла в формуле (9) через ТМ из формулы (8) при z = Ои г - 0

Тпл — Тм/exp (аt(z)Ия, /2) , подставим это выражение в зависимость (9) и преобразуем ее к следующему виду:

^Т t = ^Тм (фщ! ) / exp (^a _t ( z ) Ъ_Я1 /²) .      (10)

тпл

T , ° C

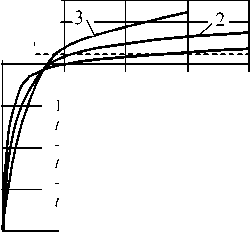
1 + 1 мм, hя = 0,6 мм, tсв = 0,1 С, Тэ = 380 °C; 2 —

— tсв = 0,08 С, Тэ = 400 °C; 3 — — 1,5 + 1,5 мм, hЯ = 2,0 мм, tсв = 0,06 с, Тэ = 430 °C;

0     0,02   0,04    0,06   0,08   t, с

1 + 1 мм, h _Я = 1,0 мм,

Рис. 5. Изменение температуры в центре контакта деталь-деталь при КТС деталей из сплава АМг6, рассчитанное по зависимости (9)

Если допустить, что характер изменения температуры по времени от нуля до ее максимальных значений в любой точке зоны формирования соединения подобен характеру изменения температуры в центре контакта деталь-деталь, то значение ТМ в зависимости (10) равно значению Тz г t рассчитанному по зависимости (8). Тогда зависимость (10) с учетом зависимостей (8) и (6) можно преобразовать к следующему виду:

TZ,r,t = Тпл (titнп )С/exp [(aZz )2 + (ar r )2 ] . (11) Зависимость (11) описывает изменение температуры в зоне сварки на стадии нагрева по координатам z и г, а также по времени t при допущении, что характер изменения температуры по времени во всех точках зоны формирования точечного сварного соединения подобен характеру изменения температуры в центре контакта де таль-деталь.

Как показывают динамика изменения размеров ядра и расчеты температурных полей численными методами, характер изменения температуры по времени в процессе сварки на периферии соединения несколько иной, чем характер в центре контакта деталь-деталь. Следовательно, величина коэффициентов a_z и а_г характеризующих градиент температуры по координатам z и г должна изменяться по времени и зависеть от условий сварки, в частности, от формы рабочей поверхности электродов.

Проведенные исследования показали, что изменение значений коэффициентов а и а в процессе КТС может быть аппроксимировано функцией вида at=a [ m -(m - 1) (titнп)n ], (12) где а и a - текущие и конечные значения коэффициента а или а при их изменении по времени; тип- экспериментально определяемые коэффициенты аппроксима ции.

Тогда формулу для расчета изменения температуры в любой точке зоны сварки и в любой момент времени в интервале 0 < t <  t_CB можно представить в окончательном виде:

^Т пл ⁽ tit нп )

Т

T z , Г , t )

exp [ ( a Zt z ) ^{2 +} ( a rP ) ²

где t - координата времени; с, а и а - коэффициенты, характеризующие изменение в процессе сварки гради ента температуры по цилиндрическим координатам z и г и времени t:

⁽ a Z h ^я /^{2 ) 2} а = ^{h( Тпл} !^тэ )          ^f h^ ²

ln (t св It нп ) , Z f2 -(hя/2)2 , Г Z [ d я J, aZt = aZ [ m1 -(m1 -1) (tit св ) n1] , art = ar [ m 2 -(m 2 - 1) (tit св ) n2 ] , где Тэ - максимальное значение температуры в контакте электрод-деталь; t - время начала плавления металла в контакте деталь-деталь; т1, и1, т2и и2 - коэффициенты (таблица), учитывающие изменение во времени градиента температуры по координатам z и г.

Известные трудности при расчетах температуры по зависимости (13) представляет точное определение для конкретных условий сварки момента начала плавления металла в контакте деталь-деталь tHn, максимальной температуры в контакте электрод-деталь Тэ, а также коэффициентов т^ и1, т2и и2. При решении научно-исследова тельских задач они в каждом случае должны определяться индивидуально. При приближенных технологических расчетах они могут быть определены по приведенным ниже обобщенным данным.

Наиболее просто определять момент t_Hn начала плавления металла в контакте деталь-деталь. Это можно осуществить прерыванием процесса сварки (с шагом 0,01 с). Установлено, что с увеличением жесткости режима сварки момент начала плавления металла t_Hn смещается к началу процесса и существует корреляционная зависимость между значением t_Hn и проплавлением деталей, выраженным отношением высоты ядра расплавленного металла Л_я к суммарной толщине деталей 2s: hyls. Усредненная для способов КТС зависимость значений t_Hn от параметра h ^ J2s, показанная на рис. 6, вполне удовлетворительно описывается функцией, интерполированной по полиному Лагранжа:

t нп = t св [ 1 - 2,776 ( h Я /2 s ) + 3,775 ( h я /2 s ) 2 - 1,8 ( h я /2 s ) 3 ] ,(14) где t_CB - время сварки; Л_я - высота ядра; s - толщина детали.

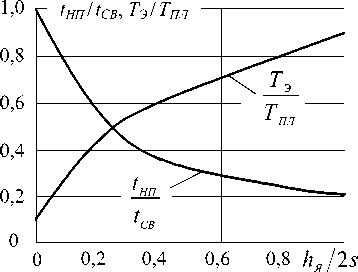
Рис. 6. Зависимость относительных значений момента начала плавления металла t_Hn/t_CB и максимальной температуры в контакте электрод-деталь Т_Э/Т_ПЛ от величины проплавления деталей h j 2s

Измерение максимального значения температуры в контакте электрод-деталь Т_э не имеет принципиальных препятствий, за исключением большой трудоемкости. Установлено, что между максимальным значением температуры в контакте электрод-деталь Т_э и относительным проплавлением деталей Л_Я / 2s существует корреляционная зависимость, показанная на рис. 6, которая удовлетворительно описывается следующей аппроксимированной функцией:

Т , Т_н ( 0,1 + 0,8 7 И_я /2 s ) , (15) где Т - температура плавления металла; Л_Я - высота ядра; s - толщина деталей.

Наиболее трудоемко определение изменения в процессе сварки коэффициентов а и а . Для этого необходимо измерять значения температуры в характерных точках (рис. 1), а затем определять значения а и а обратным расчетом по зависимости (13).

Обработкой значительного числа экспериментальных данных установлено, что характер изменения коэффициентов а и а в процессе сварки зависит в основном от геометрии рабочей поверхности электродов и жесткости режимов сварки.

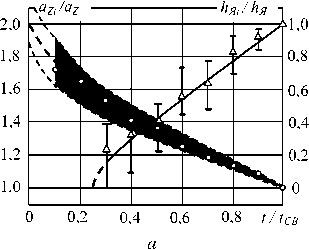
Наиболее близкий характер изменения градиента температуры по координатам z и г в процессе формирования соединения наблюдается при сварке электродами со сферической рабочей поверхностью (рис. 7). В этом случае плавление металла начинается в относительно небольшом объеме и увеличение высоты Л_Я( (рис. 7, а) и диаметра d_Я( (рис. 7, б) ядра происходит плавно. Это обусловлено тем, что градиент изменения температуры по координатамz и г в начале процесса нагрева высок, а в процессе сварки плавно уменьшается, вследствие чего монотонно уменьшаются и значения коэффициентов¹ а_zt и а_г( (рис. 7, а, б).

2,0

1,8

1,6

1,4

1,2

1,0

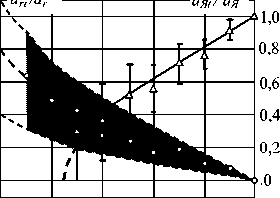
0     0,2    0,4    0,6    0,8 t/t_CB

б

Рис. 7. Изменения относительных значений коэффициентов а_г , /а_г и высоты ядра И_Я1/ к_Я (а), а также а_г1/а_г и d^/d_Я (б) в процессе сварки сферическими электродами

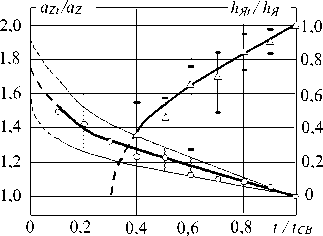
Изменения градиента температуры по координатам z и г в процессе формирования соединения при сварке электродами с плоской рабочей поверхностью различаются в большей степени, в особенности в начале процесса сварки (рис. 8). При сварке такими электродами плавление металла начинается по большей площади контакта, чем при сварке электродами со сферической рабочей поверхностью, что обусловлено меньшим градиентом температуры по координате г. Затем увеличение высоты к_Я( (рис. 8, а) и диаметра ядра d_Я( (рис. 8, б) также происходит плавно. Градиент изменения температуры по координате z изменяется подобно предыдущему, соответственно изменяется и а_zt (рис. 8, а). Градиент же изменения температуры по координате г в процессе сварки, в отличие от предыдущего случая, почти не изменяется, хотя в начальной стадии наблюдается повышенный его разброс. Это предопределяет относительно большие начальные значения диаметров ядра и относительно небольшие изменения значений а (рис. 8, б).

а

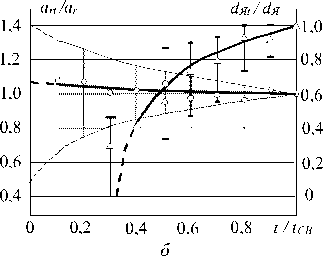
Рис. 8. Изменения относительных значений коэффициентов а21/аг и высоты ядра hl кЯ (а), а также аг1/аг и d I dЯ (б) в процессе сварки электродами с плоскими рабочими поверхностями

При точечной сварке с обжатием периферийной зоны соединения плавление металла начинается по еще большей площади контакта, чем при сварке электродами с плоской рабочей поверхностью (рис. 9). Затем увеличение высоты h^ (рис. 9 а) и диаметра ядра d_Яt (рис. 9, б) также происходит плавно. Градиент изменения температуры по координате z изменяется подобно предыдущим случаям, соответственно изменяется и а (рис. 9, а). Градиент же изменения температуры по координате г, в отличие от предыдущих случаев, в начале процесса сварки меньше, чем в конце, и монотонно возрастает в процессе формирования соединения. Это предопределяет еще большие начальные значения диаметров ядра d и увеличение значений а в процессе сварки (рис. 9, б).

Полученные таким образом значения коэффициентов а и а весьма приближенны, но, как показали сравнения расчетных и экспериментальных значений температуры и размеров ядра, приемлемы для решения приближенных технологических задач. Для практических расчетов полученные значения коэффициентов а и а обобщены аппроксимированными функциями, описывающими их изменение в процессе формирования соединений (зависимости (12) и (13)). Значения коэффициентов m_p n_p т₂ и и₂, необходимые для расчетов температуры в зоне формирования соединения для различных условий сварки обобщены в таблице.

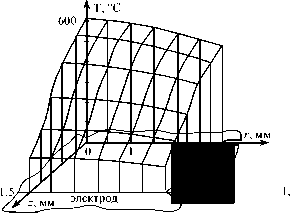
а

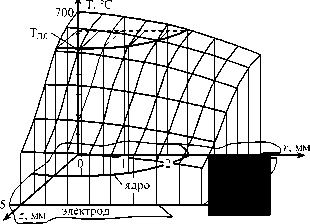
б

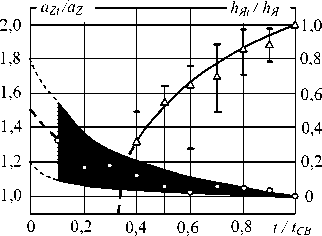
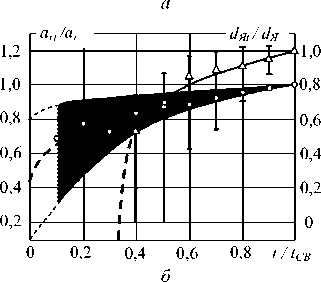
Рис. 9. Изменения относительных значений коэффициентов a_zt/a_z и высоты ядра к/ к_я (а), а также - а/ а_г и d / d „ (б) в процессе сварки с обжатием периферийной зоны соединения

Как показывают расчеты по зависимости (13) температурное поле в зоне сварки по координатам и времени отличается весьма высоким, изменяющимся в процессе КТС, градиентом температур (рис. 10).

Изменение в процессе КТС температуры по времени (рис. 11), рассчитанное по зависимости (13), в частности, в центре контактов деталь-деталь (кривая 7) и электрод-деталь (кривая 2) вполне согласуется с имеющимися данными, полученными осциллографированием и расчетами методом конечных разностей и конечных элементов.

Так, температура в центре контакта деталь-деталь (кривая 7) быстро, за время, равное 0,1...0,2 t_СВ, нарастает до значений, близких к температуре плавления, а затем рост температуры замедляется. Причем изменение температуры в центре контакта деталь-деталь, рассчитанное по формулам (11)и(13) совпадает, вследствие того, что она не зависит от координат. Изменение же температуры в контакте электрод-деталь (кривая 2), рассчитанное по зависимости (13), ближе к ее экспериментальным значениям (кривые 3), которые получены, осциллограмм (а) и пересчитанные с учетом инерционности термопары (б),

‘_СВ= 0,04 с

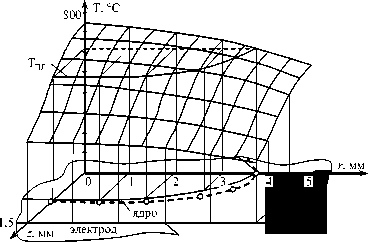
Рис. 10. Изменение температурного поля в зоне сварки, рассчитанное по зависимости (13):

АМг6, 1,5 + 1,5 мм, 7_СВ = 27 кА, Р_СВ = 6,5 кН, 1_СВ = 0,08 с, d_R = 7,3 мм, И_я = 1,6 мм: а - t = 0,02 с, б - t = 0,04 с, в - t = 0,08 с

Значения коэффициентов т _А , и_р т ₂ и п ₂ для различных условий КТС

Условия точечной сварки	Значения коэффициентов
	т х	«	m 2	« 2
Электродом со сферической рабочей поверхностью Электродом с плоской рабочей поверхностью С обжатием периферии сварной точки	1,9...2,1 1,6...1,9 1,2...1,8	0,5...0,7 0,35...0,45 0,25...0,35	1,4...2,1 1,9...2,1 0,05...0,8	0,5...0,7 0,45...0,55 0,35...0,45

Примечание: большие значения коэффициентов относятся к более жестким режимам.

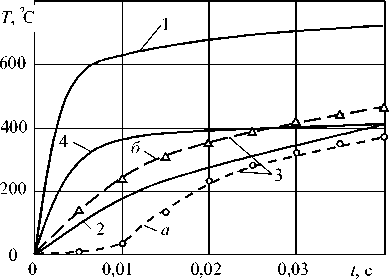
Рис. 11. Изменение температуры при КТС МА2-1,0,5+ 0,5 мм, da= 3,5 мм, Ля=0,4 мм, 7СВ= 21 кА, РСВ= 1,5 кН, чем изменение температуры (кривая 4), рассчитанное по зависимости (11). Это подтверждает целесообразность учета различия градиента температуры (изменения коэффициентов а и я ) в разных точках зоны формирования точечных сварных соединений.

Таким образом, разработан экспериментально-расчетный метод определения температуры при точечной сварке на стадии нагрева. Расчетная зависимость непрерывна и позволяет производить операции математического анализа при исследованиях термодеформационных процессов в зоне точечной сварки и решении технологических задач КТС.