Математическое моделирование транспирации и процессов переноса в почве

В рассмотрено моделирование процессов в одном из элементов гелиотеплицы - парогазовой среде. Данная работа посвящена моделированию физиологических процессов в растениях, в основном транспирации, и переноса в почве[1].

Транспирация, во-первых, обеспечивает оптимальную температуру листа, во- вторых, регулирует поступление воды и минеральных элементов в корневую часть растений, в-третьих, предотвращает возникновение избыточного давления, которое может привести к разрушению клеток растений. Транспирация также тесно ее исследование в условиях теплицы может дать существенную информацию о растениях.

При моделировании листья растений рассматриваются как случайно расположенные в заданном объеме горизонтальные пластины. Считается, что их биофизические и физиологические свойства одинаковы, площадь и масса не изменяются в течение исследуемого периода, толщина намного меньше длины.

С учетом данных допущений интенсивность транспирации с

С -С

=PC-C (1) r_s

поверхности листьев [2] j

Устьичное сопротивление в зависимости от солнечной радиации и водного потенциала листа согласно [3] rs = rs0

1 + Y

г \

V m - V l

IAW m - V l J

где    r - характерный для конкретного растения параметр, определяющий сопротивление полностью раскрытых устьиц; vm - критический водный потенциал, при котором устьица полностью закрываются; ^ - безразмерный параметр, характеризующий реакцию устьиц на изменение водного потенциала листа. В ночное время, когда I = 0, rs

^V - - ^V (3)

V m ^- V l

Явная зависимость r от температуры учитывается через водный потенциал

листа, связанный с относительной влажностью v окружающей среды [2] ,

V l = P R n ^Tl ln V ⁽⁴⁾

Выразим относительную влажность воздуха через концентрацию пара

и температуру V = ^Р П / ^Р нас   ⁽⁵⁾

Здесть   Р_п = —P-d—

П 0,622 + d

-

10,004 - ¹⁶²⁵

парциальное давление пара;   р_{а с}= 10     T ^{- 4} 8 -

давление насыщенных паров;

C d =--влагосодержание. Таким образом,

1 - C

количество влаги, испарившейся с поверхности одного листа, определяется

по (1) - (5). Если в растении N листьев, то общее количество испарившегося пара

j ^z = ? j (6)

Если предположить, что это количество влаги равно количеству воды, поступающей в растение через корневую систему, то можно считать, что на глубине l в почве имеется сток воды мощностью j .

Тепловой баланс листа ^ I = q_k + rj (7)

где q - конвективный перенос тепла с поверхности листа в окружающую среду,

2 p c p ( T l - T )

q k =------------- ^r ан

r - диффузионное сопротивление теплообмена пограничного соля листа.

Результаты экспериментов показывают, что r хорошо аппроксимируется полуэмпирической формулой [2] raH = ан I — I

I u J

( а_н - эмпирическая постоянная; b_L - - характерная длина листа). Поэтому

К I =

^          I и 1 ²

а н      I b L J

+ rj . (10)

Из (2) и (10) видно, что с увеличением интенсивности падающей радиации устьичное сопротивление уменьшается, следовательно, интенсифицируется транспирация, за счет чего температура листа будет в пределах температуры окружающей среды. В случае, когда I = 0 и TL < T испарания нет, при TL > T r опять уменьшается, что ведет к снижению TL.

В процессе функционирования гелиотеплицы почва может быть насыщенной влагой (вплоть до образования свободной поверхности воды), влажной и сухой. Если почва влажная, то процессы переноса в ней описываются уравнениями теплопроводности и диффузии [4], в сухом состоянии- только уравнением теплопроводности. Практически для теплиц важны результаты исследования процессов переноса в насыщенной влагой почве. Это обусловлено интенсивным испарением с поверхности почвы, а также переносом тепла циркулирующей жидкостью в глубь почвы. В таким состоянии уравнения сохранения основываются на модели Дарси, модифицированной Бринкманом. Учитывая ламинарность режима течения жидкость в почве, модель принимает вид [5]

d u_D дт

д P   д

---1-- д x   д x

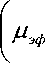
" u V-k.^ u D ^ д x )  д у [ " ■ д у J

" ж + P C* [ K * K**

I u_D\ ^U D ⁽¹¹⁾ 7

p

d» D

дт

д P д

1 д x   д x

т

Р эф V

"- дx J

д + —

Р эф

и )

+

p g в т * Л T + в с * Д с ')-

" ж + V K *

ду V рС *

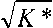
д T

'^эф a x

| ^Ud\ DD J

д T     д T

— + uD — + D_D д x      д x

д T

¹ кг л

д у   р с

' р [^{д x}

+— л

д у V

эф

77 д у JJ

дс'       д с '       дс'       ( д ² с'

--+ uD--+ dd — — DB —— дт D дx   D ду    В [дx2

+

_я2 Л д с

д у ²

’

J

д ud , дuD _Q дx     ду'

где d2(£*)3

K * —

175(1 - £ *)²

с* = 1,75(£*)^ , 1715’

Рэф — рж;

Л эф

+ £

- ^Л В ^— °-

Таким образом, получена система уравнений, описывающая физические процессы в отдельных элементах гелиотеплицы. Связывая эти модели между собой условиями сопряжения, получаем математическую модель всей системы.

Начальные условия. Считается, что в начальный момент времени вся система находится в равновесном состоянии, поэтому по всему объему и — U — 0, T — Рач , С — Снач .  (20)

Граничные условия. На рисунке схематично изображен один блок многоблочной гелиотеплицы. На твердых границах AE, BC, CD для скоростей выполняются условия прилипания [1]

u = и = 0 (21) Здесь же K = s = 0 (22)

Температура поверхности BC и CD определяется по тепловому

. д T балансу Л— + R + rjk = а ,А T, (23) д n         k       f           '

где коэффициент теплообмена между стеклом и внешней средой

1    1

a_f = 0,86 —Re² Pr³. (24)

На этих поверхностях для концентрации пара выполняются условая

— = 0, если C <  C_{m с};

^{(25) C} = ^С нас , если ^C ^ ^С н ;   ⁽²⁶⁾

на с д n

C

на с

18 Р ас

29 Р атм

- 11 Р ас

. (27)

На поверхностях AB и DE выполняются условия

симметричности или периодичности для всех исследуемых переменных (Ф = и, и, T, c', K, s):

д Ф^у) = 8 ^Ly , (28) Ф_ау ) = ФL , у ) (29) д x         д x

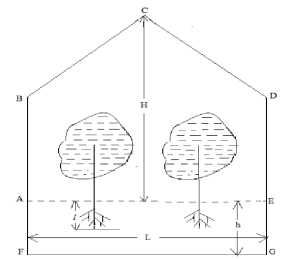
На глубине h в почве отсутствуют потоки тепла веществ, поэтому на FG

— = 0, ^ c ’ = 0. (30)

Уу       д у

Условия сопряжения. На границе грунт воздух температуры и тепловые потоки непрерывны

УТ УТ тв = L, Л ' = Л T (31)

B     2                  Эф оу       оу

Условия для материального баланса могут быть различные. В случае полива почвы с' = 1 для почвы, (32)   С = Сшс для паровоздушной среды. (33)

В других случаях выполняется условие j_n = j_B ;     (34)

т.е. с поверхности почвы удаляется столько влаги, сколько испаряется в окружающую среду

D P fsc \

1 - C U- ) гр

P b^Db

( d c ')

дУ , гр

Для поверхности листа в (5) из[1] добавляется источниковый член, связанный с транспирацией. Мощность источника определяется уравнением

Условные обозначения, принятые в статье:

K*, £ * - проницаемость и пористость среды; C * - коэффициент инерции;

c'- влагосодержание грунта; CL - концентрация паров на поверхности листьев; r - теплота парообразования; у - фактор, учитывающий чувствительность устьиц к радиации; I - плотность потока падающей солнечной радиации; Rn - газовая постоянная для водяного пара; T - температура; TL - температура поверхности листьев; рж - коэффициент вязкости воды; р - плотность; uD ,uD - скорости движения воды в почве; вт, вс - коэффициенты температурного и концентрационного расширения воды; A, D - коэффициенты теплопроводности и диффузии; R - количество поглощенной стеклом радиации; Re,Pr- числа Рейнольдса и Прандтля; PamM - атмосферное давление.