Математическое моделирование, учет демпфирующих свойств упругих связей в обобщенной математической модели системы твердых тел, установленных на упругом стержне

Анализ уравнений движения математических моделей типовых расчетных схем с упруго присоединенными твердыми телами, рассмотренных в работах [1-5], позволил предложить обобщенную математическую модель балки Эйлера-Бернулли с закрепленными краями и прикрепленными на нем с помощью упругих связей системы твердых тел, соединенных между собой упругими связями [6]. Для обобщенной математической модели на основе единого подхода был разработан аналитико-численный метод построения частотного уравнения [6].

В данной работе учитываются демпфирующие свойства в упругих связях в обобщенной математической модели [6] и развит аналитико-численный метод исследования свободных колебаний на этот случай. Отметим, что учет демпфирования в упругих связях при исследовании собственных колебаний для конкретной расчетной схемы – балка с упруго прикрепленными твердыми телами, был произведен в [7].

Постановка задачи

Рассмотрим гибридную систему дифференциальных уравнений обобщенной математической модели [6] механических систем, представляющих собой балку Эйлера-Бернулли с закрепленными краями и прикрепленными на нем с помощью упругодемпфирующих связей системы твердых тел, соединенных между собой упругодемпфирующими связями:

' Az + Cxz + C2 (Dz - u ) + Bxz + B2 (Dz — u ) = 0, d2 u       d4 u      m^f k ^(x’t) + b ^(x, t) = 2 qi(d z(t) — u(x’t)) + Pi(dz ot             dx           j=i V

—

^( x , t )) p ( x — a ).

o t       J

где z(t) - n-мерная вектор-функция; u(x, t) - скалярная функция; u (t) - m -мерная вектор-функция с компонентами u(a1, t),•••, u(am, t); A, B1, C1 - заданные постоянные n x n - матрицы; B2, C2 - заданная постоянная n x m -матрица; D - заданная постоянная m x n - матрица; di - n-мерный вектор, составленный из z-ной строки матрицы D; k, b, ax, cq, px (i = 1, m ) - заданные постоянные, причем 0 < ai < 1; (•)T - здесь и ниже операция транспонирования.

В случае жесткой заделки левого и свободного правого концов стержня функция u ( x , t )

удовлетворяет следующим граничным условиям:

u (0, t ) = 0,    ^ B- (0, t ) = 0,    | 2 u ( 1 , t ) = 0,     | 3 u . ( 1 , t ) = 0 .

o x            о x             o x

Решение гибридной системы дифференциальных уравнений (1) следует понимать в обобщенном смысле. Для введения определения обобщенного решения гибридной системы дифференциальных уравнений (1) рассмотрим множество вектор-функций

K = {(y(•), v(•,•))T : y(•) e C,[0,T], v(•, •) e C,„,G } , (3) где G = {( x, t) e R 2:0 < x < 1, 0 < t < T} - прямоугольник. Вектор-функции из множества (3), назовем основными.

Определение 1. Вектор-функцию z ( • ) e Cn^_{o r}j , скалярную функцию u ( • , • ) e C 2_{2 G} назовем обобщенным решением краевой задачи для гибридной системы дифференциальных уравнений (1), если функция u ( x , t ) удовлетворяет граничным условиям (2) краевой задачи и для любой основной вектор-функции ( у ( • ), v ( • , • ) ) T e K имеет место тождество

T

| (Az + Cxz + C2 (Dz — u) + Bxz + B2 (Dz — u)), у(t)) dt + re 1   d2 u          d4 u                                          „    du                   I

+ [[ k —-( x , t ) + b —- ( x , t ) — V q ( d T z ( t ) — u ( x , t )) + p .( d T z --( x , t )) p ( x — a .)) • v ( x , t ) dxdt = 0.

“ ( dt²          d x⁴         1:1 V........ i        d t       J          )

Для системы, описываемой гибридной системой дифференциальных уравнений (1), произведем обобщения аналитико-численного метода построения частотного уравнения [8].

Вспомогательная краевая задача

Подставив в систему (1) функции z(t ) = Ze^Xt , u ( x , t ) = V ( x ) e^Xf , где X — собственная частота, Z — n -мерный вектор амплитуд колебаний масс, V ( x ) — амплитуда колебаний точек упругого стержня, после преобразований получим

(X2 A + C + C2D + X(Bx + B2D) Z — (C2 + 2B2) V = 0,(4)

,         a 4y(x 1 m^/x

X kV (x) + b----(-) = 2^ (q; (diTZ — V (x)) + X p, (diTZ — V (x))) d( x — a,),(5)

dxii где V — m-мерный вектор с компонентами V(ax ),•••, V(am ) .

В силу того, что функция u ( x , t ) удовлетворяет граничным условиям (2), функция V ( x ) должна удовлетворять условиям:

dV       d 2Vd

V(0) = 0, —(0) = 0, — (l) = 0, — (l) = 0.(6)

dx        dxdx

Таким образом, суть исследования свелась к исследованию вспомогательной краевой задачи для алгеброическо-дифференциальной системы (4)-(5) с граничными условиями (6).

Определение 2. Функцию V(■) e C4 ^ Г] и вектор Z e Rn назовем обобщенным решением вспомогательной краевой задачи, если они удовлетворяют системе алгебраических уравнений (4), функция V(x) удовлетворяет заданному граничному условию и для любой компоненты v(■, ■) основной вектор-функции (у(■), v(■, ■))T e K, при любом t e[0, T] имеет место следую- щее тождество:

j| X2kV(x) + b - V(x) -m^qq-(diTZ2 - V(x)) + Xpt(diTZ - V(x)))5(x -at) | ■ v(x, t)dx = 0. о.                -x4    1=T                                       7

Теорема 1. При любых значениях X и Z для обобщенного решения V ( x ) дифференциального уравнения (5) справедливо представление m

V (x) = ^ G, (x - a,) ( q,( d" Z - V (a,)) + Xp,(diTZ - V (a,))),(7)

i = 1

где функции G ( x ), ( i = 1,..., m ) - обобщенные решения уравнения

XkGi(x) + b d G4(x) = 5(x),   (i = 1,...,m) .(8)

i

0 \                  dx     J

Непосредственной подстановкой (7) в левую часть (9) убедимся в том, что для обобщенного решения дифференциального уравнения (5) справедливо представление (7).

Для этого представим (7) в виде ml

V ( x ) = £j g , ( x - 5 ) ( q,(d^1TZ - V ( 5 )) + Z p , ( d*^TZ - V ( 5 )) ) - г ( ^ - a ) d ^ .          (10)

i = 1 0

Подставим (10) в левую часть соотношения (9). Далее, меняя порядок интегрирования и учитывая (8), получим llm

0 I 0 i = 1

иd ⁴ G ( x - 5 ) k Z G ( x - 5 ) + b--- ' V

,                                  4

dx

( q_t ( d ^iT Z - V ( 5 )) + X _Pi ( d"Z - V ( 5 )) ) 5 ( 5 - a₄ ) d §V v ( x , t ) dx =

m ^l

= Zj ( q , ( -^,tz - V ( 5 )) + ^ p , ( d ^,T Z - V ( 5 )) ) 5 ( 5 i = 1 0

^{- a}i ) ‘j 0

d ⁴ G ( x - 5 ) dx ⁴

v ( x , t ) dx d 5 =

l,

= Zj ( q , ( d Z - V ( 5 )) + X p , ( d"Z - V ( 5 )) ) 5 ( 5 - a ,) ‘ j v ( x , t ) 5 ( x - 5 ) dx d 5

+

i = 1 0

m ^l                                                                                                  n

= £j [ ( q , ( d^iTZ - V ( 5 )) + X p , ( dZ - V ( 5 )) ) v ( 5 , t ) 5 ( 5 - a , ) ] d 5 = £ [ ( q , ( -^itZ - V ( 5 )) + X p , ( d Z - V ( 5 )) ) v ( a , , t ) ], i = 1 0                                                                                                                      i = 1

что совпадает с правой частью (9).

Таким образом, для обобщенного решения V ( x ) дифференциального уравнения (5) справедливо представление (7). Теорема доказана.

Следствие 1. Если обобщенные решения G. (x), (i = 1,..., m) уравнения (8) удовлетворяют краевым условиям dG          d 2Gd

Gi(-a,) = 0,  -G(-a,) = 0, —f(l - ai) = 0,       (l - ai) = 0,   (i = 1,...,m),(11)

dx           dxdx то функция V(x), удовлетворяющая (7), является обобщенным решением дифференциального уравнения (5), удовлетворяющего краевым условиям (6).

Действительно, для функции V ( x ), удовлетворяющей представлению (7), справедливость выполнения краевых условий (6) непосредственно следует из краевых условий (11) для функций G ( x ), ( г = 1,..., m ).

Частотные уравнения

Для нахождения функций G_x ( x ), G ₂ ( x ),..., G_m ( x ), входящих в (7), имеем m краевых задач для уравнения

Я²kG ( x ) + b ^d G ⁽ x ) = £ ( x )                             (12)

dx4

с краевыми условиями (11).

Общее решение G ( x ) уравнения (12) можно найти в виде суммы общего обобщенного решения G _o ( x ) однородного уравнения

ЯkG(x)+b - G(x) = 0(13)

dx4

и некоторого частного обобщенного решения G ( x ) неоднородного уравнения (12), т.е.

G(x) = Go (x) + G(x) .(14)

Общее решение G _o ( x ) однородного уравнения (13) можно записать в виде

Gkx     kx     kxkx

0 (x) = cxe 1 + c2e 2 + c3e 3 + c4e 4 , где c, c2, c3, c4 - произвольные постоянные; kx, k2, k, k4 - корни характеристического уравнения, которые определяются следующим образом

, f Д Л) Л       )  , f л )  „ f 2 L k =--+,— m, k =---,— m , k, =--,— m, k. =---+,— m .

• ¹   ( 2     2 J        ²   (    2     ² J      ³   ( ²     2 J       ⁴   (    ^{2     2} J

Я k

Здесь m ⁴ =--- . Отметим, что выражение для обобщенного решения G _o ( x ) определяет общее

b комплексное решение уравнения (13). Для нахождения частного обобщенного решения G(x) неоднородного уравнения (12) воспользуемся следующим утверждением, которое является следствием общего правила нахождения фундаментального решения для линейных дифференциальных уравнений [8].

Утверждение . Если функция f ( x ) решение однородного уравнения (13), удовлетворяющее условиям

f (0) = f I (0) = f ' ¹ (0) = 0, f^HI (0) = ¹ ,                         (15)

b тогда функция

G ( x) = 0( x) f (x), где 0( x) - функция Хэвисайда,

0 ( x ) =

f 1,

I0,

x > 0, x < 0,

удовлетворяет уравнению (12) в обобщенном смысле.

Отметим, что решение однородного уравнения (13), удовлетворяющее условиям (15), найдется в виде f (x)=a (ek 2x - ek x)+a (e3x - ek1x)+a (ek4x - ekx), где i                                                i                                               i a =---------------------, a =---------------------, a =---------------------.

¹    b ( k ₂ - k)(k₂ - k₃ )( k₂ - k₄ )     ²    b ( k₃ - k_x )( k₃ - k₂ )( k₃ - k₄ )     ³    b ( k₄ - k_x )( k₄ - k₂ )( k₄ - k₃ )

Таким образом, функция g (x) = o( x) (a (ek2 x - ek1x)+a (ek3 x - ek'x)+a (ek4 x - eki x)) является частным обобщенным решением неоднородного уравнения (12).

Для нахождения обобщенных решений G (x),G (x),..., G (x) уравнения (8), удовлетво- ряющих заданным согласно поставленной задаче краевым условиям, определим произвольные константы c , c , c , c , входящие в общее решение из условий выполнения соответствую- щих граничных условий.

Далее, принимая в (7) последовательно значения x = a_x, x = a₂ ,..., x = a_m , получим систему линейных алгебраических уравнений относительно V ( a ), V ( a )..., V ( a ) :

mm

(1 + Gy(0) qj(1 + ^)V (aj) + £ G,( aj- a^ qt(1 + ^)V (a,)) = £ Gt (a, - ai) q,d" (1 + Я) Z,   (j = 1,..., m)(16)

i=1, i *j

Используя матричные обозначения, систему (16) можно записать в виде

NZ - MV = 0,(17)

где M - матрица системы размерности m x m :

• ^{2   1} + G 1 ( ⁰⁾ q 1     G 2^{( a} 1 ^{- a} 2 ) q 2 G_m ( ^a 1 ^{- a}m ) q_m

M =- v G1(am- a1) q1  G2(am- a 2) q 2.............1+Gm (0) qm    ,

N - матрица размернос N =	ти m x n mm £ G , ( a 1 - a , ) q , d ;   ^ G , ( a 1 - i = 1                                      i = 1 mm £ G, ( a 2 - a, ) q , d 1   £ G,( a 2- i = 1                                      i = 1	m ax ) qtdl2 ......£ G ( ax - i = 1 m - ax ) qd i ......£ G ( a2 i = 1	^ ai ) q i d n - ai ) q i d n
	...............................
	mm £ Gi ( am - ai ) q i d 1   £ Gi ( am v i = 1                                   i = 1	m - ax ) qtd‘2 ......£ G ( am i = 1	- a ) q i d n 7

Таким образом, объединив (17) с системой (4), получим систему линейных однородных алгебраических уравнений относительно вектора амплитуд Z и V :

( Я² A + C + C₂D + Я ( B_x + B₂D ) Z - ( C ₂ + Z B₂ )V = 0,

NZ - MV = 0

.

Система (18) имеет ненулевые решения, если ее определитель равен нулю. Приравняв определитель системы (18) к нулю, получим уравнение собственных частот:

2 Я 2 A + C + C2D + ^ ( B + B2D ) et v              N

C2 + ZB2 ) 2      2   = 0.                      (19) M j

Отметим, что уравнение собственных частот (19) является трансцендентным, имеющим бесконечный дискретный набор собственных частот.

Пример. Сравнительный анализ

Рассмотрим консольный стержень с установленными на пружинах тремя твердыми телами (рис.). Левый конец стержня жестко закреплен, а правый свободен. Твердые тела массы m , m , m установлены на пружинах с коэффициентами жесткости c , c , c на расстояниях a_x, a₂, a₃ от левого конца стержня и совершают поступательные перемещения z_x ( t ) , z ₂ ( t ) , z ₂ ( t ) в направлении осей O_xz_x, Op, O₃z₃ . Здесь точки O_x , O ₂, O ₃ совпадают с положениями равновесия тел. Перемещения точек стержня описываются функцией u ( x , t ) .

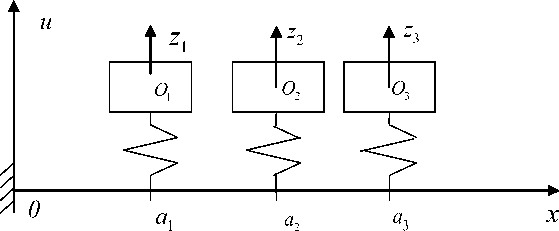
Рис. Расчетная схема системы «консольный стержень с тремя осцилляторами с демпфированием»

Гибридная система дифференциальных уравнений, описывающая движение рассматриваемой системы, полученная на основании принципа Гамильтона, имеет вид:

mxzx + b (zx — du (a, t)) + cx (zx — u (ax, t)) = 0, m2z'2 + b2 (z2 — Cu (a2, t)) + c2 (z2 — u (a2, t)) = 0 m3z3 + b3 (z3 — du (a3, t)) + c3 (z3 — u (a3, t)) = 0,

PF lu + EJ 4u = [ C (zi— u (x, t)) + b(zi д t2       dx4 I          x ’

—

du (x,t))>(

x—a)+

+ с2 (z2

—

du dt

(x, t)) 5 (x — a2) +

⁺ c 3 ⁽ Z 3

—

—

^ (x, t)) j5 (x — a3)

где p— объемная плотность материала стержня; F — площадь поперечного сечения стержня;

E, J — соответственно модуль упругости первого рода материала стержня и момент инерции поперечного сечения стержня относительно оси, проходящей через центр тяжести сечения, перпендикулярной плоскости изгибных колебаний стержня соответственно; b — коэффициент вязкого трения материала пружины. На функцию u ( x , t ) наложены краевые условия (2). Гибридная система дифференциальных уравнений (20) является частным случаем, предложенной обобщенной математической модели (1).

Для проведения сравнительного анализа предложенного подхода были использованы данные модели и расчеты, приведенные в работе [7]: l = 1 m - длина консольного стержня; pF = 0,675 kg/m - масса единицы длины стержня; J = 5, 20833^10-|° т4 - масса единицы длины стержня в момент инерции поперечного сечения относительно нейтральной оси, проходящей через центр тяжести сечения и перпендикулярной плоскости колебаний стержня; ai=0,1 m, a2=0,1 m, аз=0,1 m — точки, в которых крепятся осцилляторы; bx = 0,1 Ns/m, b = 0,1 Ns/m, Ьз=0,1 Ns/m — коэффициенты вязкого трения; с, = 0,1 N/m, сг = 0,1 N/m, с = 0,1 N/m, — коэффициенты жесткости пружин в осцилляторах; E = 7 • 1010 N / m2 — модуль Юнга.

Расчеты первых двух собственных частот, полученные методом, предложенным в данной статье:

Л = - 0,255 + 25,839 ? ,    Л = - 0,235 + 161,938 ? .

Расчеты соответствующих частот, приведенные в работе [9]:

^ = - 0,255 + 25,839 ? ,    ^ = - 0,235 + 161,941 ? .

Как видно, полученные результаты имеют хорошее совпадение.

Заключение

К обобщенной математической модели, представляющей собой систему взаимосвязанных твердых тел, прикрепленных упругодемпфирующими связями к упругому стержню, предложен единый подход к построению частотного уравнения. Выполненный сравнительный анализ численных расчетов предложенным методом с расчетами, проведенными другими способами, известными из литературы, показал достоверность и универсальность предлагаемого подхода.

Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов № 12-08-00309а, № 15-08-00973а.