Математическое моделирование в микрофлюидике: основные положения

Условные обозначения:

Re — число Рейнольдса;

Re критич. — критическое значение числа Рейнольдса;

U — характерное значение скорости;

d — характерный геометрический размер;

ρ — плотность;

µ — динамический коэффициент вязкости;

R — радиус круглого микроканала;

g r ( g d ) — гидродинамический радиус (диаметр);

2 h — ширина щели;

b ( a ) — ширина (глубина) прямоугольной щели;

δ — толщина вытеснения;

l — длина пластины;

u _*— скорость конвективного движения;

• V ^* — максимальная скорость;

• < V >  — средняя скорость;

V δ — скорость на границе пограничного слоя;

S — площадь сечения канала;

P — периметр сечения;

r ₁, r ₂ — внутренний и внешний радиусы коаксиала;

ml — медиана треугольного сечения;

U ( z ) — распределение скорости по сечению щели;

y — ортогональная координата (координата сечения);

z — нормированная координата сечения щели ( z = y / h );

Kn — число Кнудсена;

λ — длина свободного пробега в газе или жидкости;

V — молярный объем;

Na — число Авогадро 6.02214∙1026 моль–1;

r s — радиус Стокса;

R g — радиус инерции частицы;

n i — число жестких звеньев;

δ _l — длина одного жесткого звена молекулы;

С — концентрация анализируемого вещества;

τ — касательное напряжение в среде;

ε — диэлектрическая проницаемость;

ζ — дзета-потенциал;

Т — абсолютная температура;

Т ^* — характерная температура внешней среды (298 К);

T_* — нормированная разность ( Т – Т ^* )/ Т ^*;

h^* — коэффициент, пропорциональный коэффициенту теплопроводности k ;

σ — постоянная Стефана—Больцмана;

w ( T ) — плотность энергии излучения;

r — текущая радиальная координата;

kr , Wr и Λ — вспомогательные параметры, определяемые геометрией коаксиала;

g — проекция гравитационного ускорения на аксиальную координату х ;

D — коэффициент диффузии;

χ — коэффициент термодиффузии;

• l i — валентность i -го иона;

• е — заряд электрона;

• F — постоянная Фарадея;

• с 0 — молярная концентрация ионов компонент;

• k_b — постоянная Больцмана;

• φ — потенциал;

sh (ch) — функция гиперболического синуса (косинуса);

• λ D — длина Дебая;

• q — заряд частицы;

• I₀ — цилиндрическая функция Бесселя нулевого порядка первого рода;

Е — напряженность электрического поля;

• D ^* = D / h ², u ^* = V ^* / h — нормированные коэффициент диффузии и максимальная скорость;

Pe — число Пекле;

ПДМС — полидиметилсилоксан;

ПММА — полиметилметакрилат;

ПК — поликарбонат;

ПЕТ — полиэтилтетрахлорид.

Среди последних концептуальных публикаций, связанных с развитием микроаналитических систем и в первую очередь реализацией электрофореза на микрочипе, имеются статьи различной направленности. При этом основными направлениями исследований являются: а) анализ и изучение физико-химических явлений, происходящих в ми-кроразмерных системах, и разработка математических моделей процессов переноса и взаимодействия веществ в микроканалах [1-3]; б) создание новых архитектур (топологий) микрочипов для выбранных методов анализа [4]; в) разработка высокочувствительных и селективных аналитических методов на микрочиповой платформе [5-7]; г) развитие нанотехнологий получения микроразмерных устройств [8-10]. Нетрудно убедиться, что первое направление работ непосредственно связано с моделированием как натурным, так и имитационным; второе, третье и четвертое направления, по-видимому, должны включать математическое моделирование в качестве предварительного этапа работ.

Широкое разнообразие и взаимозависимость процессов переноса вещества и энергии (тепла) в сочетании со спецификой микрофлюидики (прежде всего микроразмеры конструктивных элементов микрофлюидных аналитических систем), а также необходимость развития методик анализа различных по природе, размерам и иным характеристикам объектов требуют изложения основополагающих моделей процессов. Бесспорные широкоизвестные преимущества математического моделирования позволяют решать задачи оптимизации конструкции микрофлюидной системы или ее отдельных элементов, а также осуществлять оптимальный выбор режима анализа или любых его стадий еще до проведения конструкторско-технологических работ.

В данной статье не будут рассматриваться различные постановки задач оптимизации, а также формулироваться ограничения разной природы — физико-химические, конструктивно-технологические и организационно-финансовые. Кроме того, поскольку рассматриваются физико-химические процессы переноса вещества и энергии, математические модели в большинстве своем имеют форму систем дифференциальных уравнений второго порядка в частных производных. Методы решения таких уравнений — аналитические (Фурье и его модификации, например, метод Гринберга, Галеркина, в ряде случаев метод Даламбера и функций Грина, операторный метод Лапласа и т. д.) или численные (явные или, что более эффективно, неявные конечно-разностные схемы), они традиционны. Развитие затрагивает в основном численные методы и идет по пути экономии использования вычислительных ресурсов и увеличения быстродействия современной вычислительной техники.

С точки зрения постановки задач математического моделирования процессов в микрофлюид-ных системах основополагающим является формулировка базовых принципов. К таковым можно отнести: 1) гипотезу ламинарности потоков (иногда ее полагают само собой разумеющейся, если речь идет о микрофлюидике); 2) гипотезу сплошной среды (границы ее применимости); 3) законы формирования скоростного профиля, массопере-носа, распределения электрического и теплового полей; 4) граничные условия, связанные с геометрией элементов конструкций (стенки каналов, зоны смесителей потоков и т. д.).

Перечисленные выше и связанные с ними положения, определяющие постановки математических моделей и являются главным предметом статьи.

ГИПОТЕЗА ЛАМИНАРНОСТИ ПОТОКОВ

Микрофлюидика в своей основе предполагает движение жидкости или газа в микроканалах. Последние имеют размеры сечения от 1 мкм до 1 мм, хотя наиболее распространенными считаются размеры 30-300 мкм [11].

Как известно, ламинарность потока связывается с величиной числа Рейнольдса — одного из базовых показателей подобия гидродинамических явлений. Его величина определяется как

Re = Ud P ,

µ

где U и d — характерные скорость потока и геометрический размер канала; р и р — плотность и коэффициент динамической вязкости среды соответственно. Заметим, что понятия характерных скоростей и размеров не имеют однозначной интерпретации. Этот вопрос будет обсужден позже. Однако очевидно, что от выбора указанных характеристик будут зависеть результат вычисления (1) и правила определения границ ламинарного и турбулентного режимов.

В случае сложной формы сечения в качестве характерных размеров используют гидродинамический (или гидравлический) диаметр — gd, определяемый как gd = 4S/P, где Su P — площадь и периметр сечения соответственно. Нетрудно убедиться в том, что в простейших случаях сечений гидродинамический диаметр совпадает с естественно выбираемым характерным размером. Например, в случае круглого сечения gd = 2R (диаметр круглого канала), плоской щели — gd =25 (удвоенная высота щели), коаксиального капилляра — gd= 2(r2- r 1), прямоугольного сечения — gd= = 2ab/(a+b) (гармоническое среднее ширины и высоты сечения), равностороннего треугольника — gd = 2ml/3, где ml — медиана (т. е. совпадает с расстоянием от вершин треугольника до его центра тя- жести). В табл. 1 представлены характеристики микропотоков, реализованных в различных каналах.

Табл. 1. Характеристики микропотоков, реализованных в различных каналах

Числа Рейнольдса	Среда	Описание канала	Публикация
30–20000	Азот	Круглый; диаметр 3–81 мкм	[12]
До 600	Вода	Трапецеидальный; длина 12–36 мм, глубина 27–63 мкм, ширина 100–1000 мкм	[13]
Для круглого — до 1, 2; остальные — не рас-cчитаны	»	Круглый; диаметр 8–42 мкм; прямоугольный, трапецеидальный и треугольный; длина 2.5–10 мм, глубина 13.4– 46 мкм, ширина 35–110 мкм	[14]
До 2500	»	Круглый; диаметр 50–254 мкм	[15]
1–18	»	Массив прямоугольных каналов; глубина 30 мкм, ширина 600 мкм, длина 3 мм	[16]
0.001–1	»	Массив прямоугольных каналов; глубина 22.61– 26.35 мкм, ширина 150–600 мкм, длина 7.75 мм	[17]
50–4000	»	Прямоугольный; глубина 100–300 мкм, ширина 200–400 мкм, длина 50 мм	[18]
Жидкости: <<1 до 80	n-Пропанол, силиконовое масло, азот, гелий	Прямоугольный и трапецеидальный; глубина 0.48– 38.7 мкм, ширина 55–115 мкм, длина 10.2–10.9 мм	[19]
10–1450	Вода	Трапецеидальный; глубина 28–114 мкм, ширина 148–523 мкм, длина 28 мм	[20]
50–2500	»	Круглый; диаметр 75–242 мкм	[21]
200–600	»	Массив травленных прямоугольных/ трапецеидальных каналов; глубина 50–56 мкм, ширина 287– 320 мкм, длина 1 см	[22]
Вода: 17– 126	Вода, биологические (флюиды)	Трапецеидальный; глубина 20–40 мкм, ширина 40– 150 мкм, длина 11.7 мм	[23]
200–15000	Азот, гелий, аргон	Трапецеидальный U-образный; глубина 28– 65 мкм, ширина 133–200 мкм, длина 7.6–40.3 мм	[24]
200–20000	Азот, вода	Круглый; диаметр 19–102 мкм	[25]
1–10	Смесь: вода + глицерин и вода	Специальный смеситель	[26]
50, 100, 470, 900	Вода	Прямоугольный; глубина 115 мкм, ширина 200 мкм, длина 24 мм	[27]
<0.1	»	Круглый; диаметр 100 и 205 мкм, длина 14 см	[28]
0.1–10	»	Прямоугольный; ширина 10–100 мкм, глубина 3 мкм; призматические элементы высотой 0.1–2 мкм	[29]

Табл. 2. Критические значения чисел Рейнольдса, при которых возможен переход к турбулентному движению

Критическое число Re	Вид сечения канала	Характерный размер	Публикация
2400	Плоская щель	2 h	[30]
2300	Круглая труба	2 R	[31]
2000	»	2 R	[32, 33]
300–1500	»	2 R	[34]
50000	Бесконечная тонкая пластина	l	[34]
2100	Плоская щель, круглая труба	2 h	[35, 36]
2000–2800	Коаксиальный капилляр	g d	[37]
1100	Круглая труба	2 R	[38]
2000	Плоская щель, круглая труба	2 h , 2 R	[39]
500000	Бесконечная тонкая пластина	l	[39]
100000	»	l	[40]
300	Круглая труба, коаксиальный капилляр	g r	[41]
6300	Бесконечная тонкая пластина	l	[41]
2000–2500	Круглая труба, коаксиальный капилляр	g d	[42, 43]
2000–7700	Круглая труба, коаксиальный капилляр	g d	[44]
5314	Плоская щель	2 h	[45]
7084	»	2 h	[45]
420	»	δ (*)	[45]
1070–1125	»	2 h	[45]
340–527	Плоский диффузор	2 h	[46]
1050	Квадратная труба	а	[47]
1260	Прямоугольная щель ( b / a < 3)	a	[48]
800–1400	Прямоугольная щель ( b / a < 30)	a	[45]
955–1050	Прямоугольная щель ( b / a <100)	a	[48]
1000–1344	Круглая труба	R	[47]
1050–1075	Коаксиальный капилляр	g r	[49]
10	Разделительная сетка	2 h	[50]
500	Мембрана	R	[51]
300000	Бесконечная тонкая пластина	l	[31]

Примечание. * — Под толщиной вытеснения δ для плоской щели понимается по анало- 1

гии с [32] величина δ = V ^{* - 1} _∫ ( V ^* - U ( _z ))d _z , где U ( z ) — распределение скорости по сече- 0

нию щели, z — нормированная ширина щели.

Для идентификации указанных режимов изучалась зависимость критических значений чисел Рейнольдса, определяющих переход к турбулентному режиму, от выбранного критического размера ( d ) и других показателей (скорость, тип сечения канала и т. д.). Некоторые из критических значений приведены в табл. 2. Сопоставление данных табл. 1 и 2 позволяет сделать вывод о том, что при движении жидкостей в каналах достаточно редко достигается турбулентный режим. В то же время движение газов, как правило, турбулентное. Вместе с тем некоторые из режимов, представленные в табл. 1, в частности (см. [21]) движение воды в круглом канале радиуса до 242 мкм с числами Рейнольдса до 2500, находятся близко или за границей ламинарного режима.

Также следует отметить, что как выбор характерного размера, так и соответствующее критическое значение числа Рейнольдса существенно различаются. Остается дискуссионным вопрос, следует ли оценивать ламинарность потока, исходя из поперечного числа Рейнольдса (взяв гидравлический диаметр в качестве характерного размера), либо следует оценивать продольные числа Рейнольдса, выбрав характерным размером длину канала, как правило, на 2–3 порядка большую. При этом правила выбора критического числа Рейнольдса, по-видимому, также будут различны. Например, рассмотрим микроканал прямоугольного сечения с соизмеримыми шириной и глубиной порядка 100 мкм и длиной 20 мм. С одной стороны, допустима интерпретация конструкции как "прямоугольная щель" ( b/a < 3) c Re критич. = 1260 [47] и расчетами, основанными на величине глубины канала; в то же время возможна и интерпретация микропотока, обтекающего бесконечную плоскую пластину, каковой является дно и стенки канала с характерным размером — длиной канала и другими критическими числами Рейнольдса [34, 39–41].

Главной особенностью описанных режимов является управление давлением, а не электрокинети-ческое управление. Исключение составляют [26, 28, 29]. Возможно, что имеющиеся при электроки-нетическом управлении традиционно признанные ограничения тепловой мощности, а следовательно и величины напряженности продольного электрического поля, приводят к недостижимости турбулентных режимов. Следствия указанных ограничений будут проанализированы далее.

ГИПОТЕЗА СПЛОШНОЙ СРЕДЫ

Важнейшим положением, нуждающимся в проверке, является допустимость анализа массопере-носа вещества на основе модели сплошной среды, что позволяет использовать концентрационные зависимости вместо статистического анализа ан- самбля отдельных частиц. В [11] положение о модели сплошной среды рассматривается как необходимое условие микрофлюидики. Анализ применимости гипотезы проводится на основе сравнения длины свободного пробега частицы с характерным размером сечения. Данный критерий — критерий Кнудсена — требует оценивания еще одного показателя гидродинамического подобия:

Kn = λ / d ,                  (2)

где λ — длина свободного пробега в газе или жидкости.

На основе оценок (2) числа Кнудсена определяются два важных положения: а) при Kn более 10^–3 следует учитывать неравновесные эффекты в среде; б) при Kn от 10^–3 до 10^–1 гипотеза сплошной среды еще правомерна и, кроме того, допустимо применение условия прилипания частиц к жестким стенкам канала. Сама формулировка последнего условия также может быть различна: как в форме U = 0, так и в более сложной форме, связанной с касательными напряжениями. Данные выводы сделаны на основе работ [52–55].

Расчет λ можно осуществить в соответствии с формулой [56]

λ ≈ ³ IV /Na ,                 (3)

где V — молярный объем, Na — число Авогадро. Для воды λ = 0.3 нм [11] и даже в микроканале 1 мкм число Кнудсена составляет 3.10^–4. Тем самым гипотеза сплошной среды, бесспорно, применима.

Длина свободного пробега (3) может быть вычислена как λ ≈ 1/( у/ 2 πr _s ²Na), если использовать в качестве r s радиус Стокса как следствие сферической аппроксимации частицы. С другой стороны, для модели жесткоцепной молекулы характерный размер частицы — радиус инерции R g , вычисляемый как R = ^{n i ⋅ l} [57, 58].

g ₆

Например, полагая длину одного основания фрагмента ДНК ( δ l = 1 bp) как 3.4 Ǻ, получаем для одноцепочечного фрагмента n i = 100 bp — R g = = 14 нм, если предположить фрагмент ДНК жесткоцепной молекулой. Однако критическим в этой ситуации будет применение модели сплошной среды не к веществу, а к буферу. В случае водоподобного буфера следует брать радиус Стокса молекулы воды и оценивать для воды длину свободного пробега, поскольку наименьшим радиусом Стокса и наибольшей длиной свободного пробега, а следовательно и числом Кнудсена, будут обладать самые маленькие частицы в рассматриваемой системе.

Таким образом, для микроканалов (т. е. каналов с гидравлическим диаметром сечения более 110 мкм) гипотеза сплошной среды выполнена. Следовательно, два основных нерасторжимых признака микрофлюидики — сплошная среда и ламинарность конвективного движения — не опровергнуты, в том числе и различными экспериментами!

Остальные положения: схемы загрузки анализируемой пробы, модели формирования скоростного профиля, уравнения массопереноса, уравнения формирования электрических и тепловых полей и связанные с ними граничные условия на жестких стенках канала — не являются универсальными, присущими исключительно микрофлюиди-ке, и зависят от типа микрофлюидной системы. Например, основополагающим является способ управления веществом: градиент давления или электрического поля. Указанные особенности реализации и моделирования микрофлюидных систем с разных позиций исследованы в работах [59-77].

СХЕМА ПЕРЕНОСА ВЕЩЕСТВА

Основная рассматриваемая схема — движение короткой пробки по длинному тонкому каналу. Прежде всего этой генеральной схеме соответствуют все режимы измерений, представленные в табл. 1 [12-25]. Кроме того, характерные размеры сечения укладываются не только в микродиапазон, но и в указанный в [11] интервал 30300 мкм.

Эта же общая геометрическая схема — длинный тонкий канал с пробой в виде короткой "пробки" реализуется в [59, 69, 70]. При этом в [70] исходная "пробка" аппроксимируется дельта-функцией, в [59] пробка аппроксимируется либо гауссовым распределением, либо равномерным (ограниченным длиной). В рассматриваемом [7277] случае речь также идет о длинном микроканале трапецеидального сечения (средняя полуширина 20-70 мкм, глубина 10-20 мкм и менее) и при равномерно заполненной пробке длиной до 1 мм. Объему пробы 100 пл при полуширине 20 мкм и глубине 10 мкм (т. е. самая длинная пробка) соответствует длина пробки 0.25 мм.

Сечение канала, как правило, круглое или канал представляет собой плоскую или прямоугольную щель [12-25], и реже анализируются сечения иной формы [70] (эллиптическое, треугольное или трапецеидальное). В [69] параметры прямоугольного сечения микроканала: глубина 20 мкм, ширина 200 мкм при длине несколько сантиметров.

В [70] схема аналогична: ширина канала 50 мкм, средняя скорость конвективного движения около 1 мм/с. Нетрудно убедиться, что указанный режим, предложенный для чип-реализации элек- трофореза, при водоподобном буфере с ц/р = =10-2 см2/с обеспечивает ламинарность потока с большим запасом: Re = 0.05. Даже так называемые продольные числа Рейнольдса, использующие в качестве характерного размера длину канала, например 3 см, приводят к оценке Re = 30, что также далеко от перехода к турбулентности.

ГРАНИЧНЫЕ УСЛОВИЯ НА СТЕНКАХ МИКРОКАНАЛОВ

Традиционным граничным условием на стенке канала является ее непроницаемость для вещества. Это условие в форме д C / д z = 0 достаточно очевидно, и нет веских оснований для его опровержения.

Наложение аналогичных условий на скоростной профиль (конвективную скорость в микроканале) и на распределение температуры уже допускает различные подходы и трактовки.

• 1.    Следствием уравнения неразрывности для несжимаемой ньютоновской жидкости при отсутствии гравитационных и электрических сил можно считать утверждение в форме д и / д z = 0. Это условие может быть рассмотрено вблизи жесткой стенки. Как следствие, поскольку т = ц -д и / д z , — равенство нулю касательного напряжения на стенке.

• 2.    При не слишком больших скоростях, малых размерах и отсутствии электрокинетических эффектов [1], т. е. при U/g d менее 10¹² с^-1, граничное условие на стенке U = 0 допустимо.

• 3.    В ряде случаев границей можно считать границу слоя Штерна внутри двойного электрического слоя, и условие задается на этой границе в форме и = -eZ E / Ц , где £ — диэлектрическая проницаемость, Z — дзета-потенциал, ц — динамическая вязкость. Формально это условие не является граничным. Подобный подход принят в ряде работ [11, 78-80]. При этом на режим наложен ряд основополагающих ограничений: а) однородность дзета-потенциала; б) малость толщины двойного электрического слоя по сравнению с размерами сечения микроканала; в) электрически изолированная стенка канала; г) малые числа Рейнольдса (ламинарность); д) малое произведение чисел Рейнольдса и Струхаля (дополнительно к предыдущему, малая нестационарность); е) однородность характеристик потока; ж) параллельность входного и выходного потоков.

Граничные условия на стенках канала применительно к моделированию процессов теплопере-носа анализируются, исходя из данных табл. 3 и 4.

Сравнение приведенных характеристик для воды свидетельствует о корректности температурных аппроксимаций, приведенных в табл. 3.

Табл. 3. Аппроксимация температурных зависимостей физико-химических характеристик вещества и материала микрочипа (по данным [68])

Характеристика	Жидкость (среда)	Стекло (стенка)
Плотность p , г/см3 Теплоемкость С р .103, Дж/(моль. К ) Коэффициент теплопроводности k , Дж/( К ∙м∙с) Молярная электропроводность X , м2/(Ом^моль) Динамическая вязкость ц , кг/(см) Диэлектрическая проницаемость £	1.00 4.18 0.61 + 0.0012( T - T *) 12.64 - [1 + 0.025( T - T *) ] 10 - 3 2.761 - exp(1713/ T ) - 10 - 6 305.7 - exp( - T /219)	2.15 1.00 1.38 + 0.0013 - ( T - T *) — — —

Табл. 4. Физико-химические характеристики веществ при 1 атм. давлении и 15 ^оС [11]

Вещество	Динамическая вязкость, г/(с∙см)	Кинематическая вязкость, см2/с	Коэффициент теплопроводности k , Дж/(К∙см∙с)	Коэффициент термодиффузии, см2/с
Вода	0.0114	0.0114	0.0059	0.00140
Этиловый спирт	0.0134	0.0170	0.00183	0.00099
Глицерин	23.3	18.50	0.0029	0.00098
Воздух	0.000178	0.145	0.000253	0.202

Оценка коэффициента динамической вязкости: по табл. 4 для воды при 15 ^оС (288 К) эта величина 0.0114 г/(см∙с) или 1.14∙10^–3 кг/(м∙с). Аппроксимация зависимости ц = ц (T ) из табл. 3 дает величину 1.057∙10^–3 кг/(м∙с).

Оценка коэффициента теплопроводности дает количественно схожие величины: 0.598∙10^–4 (аппроксимация зависимости, табл. 3) и 0.59∙10^–4 Дж/(м∙К∙с) (табл. 4).

Кроме того, совершенно очевидно (см. табл. 3), что стеклянная стенка микроканала не является теплоизолирующей. Таким образом, условие непроницаемости (граничное условие второго рода) на стенке для температурного поля неприемлемо!

В [68] сформулировано граничное условие третьего рода — ньютоновский поток ~

| T + h* - T = 0,               (4)

д z где T представляет собой нормированную разность температуры с* температурой внешней среды, а коэффициент h* пропорционален коэффициенту теплопроводности k стенки. Следует подчеркнуть, что указанное условие (4) достаточно традиционно в задачах теплообмена. В частности, оно подробно обсуждается в [81]. В принципе модель ньютоновского потока является следствием линеаризации закона Стефана для плотности энергии излучения абсолютно черного тела в форме w(T) = oT4, где a — постоянная Стефана— Больцмана вблизи стенки микроканала.

БАЗОВЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Скоростные и концентрационные профили

Теоретическую основу составляют а) уравнение неразрывности с системой уравнений Навье—

Стокса (для ввода вещества давлением); б) система уравнений Пуассона—Больцмана для электростатического потенциала и для скоростного профиля (для электрокинетического управления потоками); в) дополнительно к предыдущему, теория двойного электрического слоя; г) при наличии нескольких побудителей движения потока, например давление и электрокинетика, соответствующие конвективные скорости складываются. Такая аддитивность следует из принципа суперпозиции только при условии линейности!

При управлении давлением распределение конвективной скорости в круглом микроканале и коаксиальном капилляре имеет вид соответственно

ный вид: правая часть должна содержать D А C. Она позволяет численно рассчитывать нестационарный скоростной и концентрационный профили в трехмерном пространстве.

В частности, система уравнений Навье—Стокса для компонент скорости v i , i = 1, 2, 3 представляется в форме

v = ^{ v 1 , v 2 , v з ^} .

U = V * (1 - r ² / R 2 ),

Wr

(

r

.

Уравнение (6) представлено в [32, 34, 38] в несколько иной форме. Здесь r — радиальная координата сечения микроканала (коаксиала); R — радиус канала; r 1,2 — внутренний и внешний радиусы коаксиала; максимальная V ^* и средняя < V > скорости пропорциональны градиенту давления; вспомогательные параметры определяются геометрией коаксиала — k- = - 2 / - 1 ; Л = - ( k- "² - 1)/ln( k- );

W- = k- -2 + 1 - л .

Первые результаты (5) и (6) были приведены в классических работах [82–84] и очень хорошо известны с середины XIX века. Аналогично круглому каналу описывается скоростной профиль в плоской щели с точностью до замены радиусов на полуширину щели. Все эти результаты получены исходя из уравнения Навье—Стокса в приближении Пуассона при дополнительном предположении о наличии только аксиальной составляю-

Здесь v — вектор скорости конвективного движения. Чаще всего в прямолинейных каналах мик-рофлюидных систем он имеет только одну аксиальную составляющую [11]. Систему Навье—Сто-кса (8) традиционно дополняет уравнение неразрывности (сплошности) pV v = 0.

Для расчета массопереноса (профиль концентраций C = C ( x , y , z , t )) и теплопереноса (профиль температур Т = Т ( x , y , z , t )) используются аналогичные уравнения с заменой коэффициента динамической вязкости ц на коэффициент диффузии D или термодиффузии % . В правой части уравнений (8) производится замена "вязкого" слагаемого ц А v на диффузионное D А C или термодиффузионное х А T соответственно, и также могут быть дополнительные источниковые/стоковые слагаемые, связанные с выработкой или расходованием вещества или тепла. Заметим, что такой вид имеют уравнения при предположении о постоянстве коэффициентов динамической вязкости, диффузии и термодиффузии.

щей вектора конвективной скорости движения:

А u = IdC p - p gx ) , ц    d x

где g — проекция гравитаци-

онного ускорения на аксиальную координату х .

Оператор Лапласа традиционно обозначен как А .

При этом же предположении распределение концентраций будет описываться как

Двойной электрический слой и распределение поперечного электрического поля

Рассмотрим уравнение Пуассона—Больцмана для распределения потенциала в случае симметричного электролита с двумя моновалентными ионами:

2 2 ^ = 2F11C». si/ le*; )' dz ² Е [ k b T J

.

dC + U (у)   = D д t        дx

д ² C д ² C д x ² д у ²

Здесь C = C ( x , y , t ) — распределение концентрации вещества; U ( y ) — профиль аксиальной составляющей конвективной скорости; x — аксиальная координата; y — ортогональная координата сечения; D — коэффициент диффузии. (7) соответствует модели плоской щели. Система уравнений Навье—Стокса имеет в общем случае более слож-

Здесь l i — валентность i -го иона, е — заряд электрона, F — постоянная Фарадея, с 0 — молярная концентрация ионов компонент, Т — температура, k b — постоянная Больцмана, φ — потенциал, z — нормированная пространственная координата сечения, sh — функция гиперболического синуса. Теоретические исследования уравнения (9) проводились в работах [85–87].

Выделяют два пристеночных слоя [11]: слой Штерна (Stern layer) и Гоуи—Чепмена (Gouy-Chapman layer), причем толщина второго связана с дебаевской длиной электролита X D . В большинстве случаев допускается линеаризация уравнения

Пуассона—Больцмана и использование т. н. приближения Дебая—Хаскела. В частности, оно использовано для оценки X _D в работах [86, 87].

Для второго варианта (11) получено явное выражение скоростного профиля для круглого микро-

X d

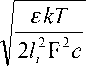
канала r = a [91]:     u ( r ) = ^£ZL 1 - ° ^{( r}' ^^d) ,

Ц I       I 0 ( r / a ) )

где I0 — цилиндрическая функция Бесселя нулевого порядка первого рода. Качественно схожим бу-

При типичной биохимической концентрации буфера 10 мМоль эта величина (10) составляет несколько нанометров [86]. Характерной величиной дзета-потенциала является 50 мВ [11].

Важная физико-химическая характеристика анализа — толщина двойного электрического слоя составляет несколько X _D. В частности, в [28] говорится о четырехкратной дебаевской длине при X _D = 3 нм. Количественно эта толщина при традиционных условиях анализа оценивается около 10 нм [29]; в [68] упоминается о единицах-десятках нанометров по сравнению с микрометровыми размерами канала. В [11] утверждается, что типичным является отношение X _D/ g d <  10 - 4 . Другая характеристика — величина потенциала на границе слоя Штерна, называется дзета-потенциалом ( Z ). Именно эту величину (порядка 10-100 мВ) используют в качестве граничного условия (потенциал на стенке канала) для решения уравнения Пуассона—Больцмана. Вторым естественным граничным условием для симметричной конструкции берется симметрия электрического профиля в форме др / д z = 0 на геометрической оси микроканала.

На основе предыдущего приближения были рассмотрены профили электроосмотического потока, а также результирующий (аддитивный) профиль [88, 89, 91-93]. Результирующий профиль складывался из электроосмотической составляющей и из составляющей, обусловленной градиентом давления или электрофоретической подвижностью [68]. Так, в работе [88] составляющая, вызванная градиентом давления, описана уже практически упомянутым ранее дифференциальным уравнением A u = V p / ц .

В [89] исследовалось влияние дзета-потенциала на электроосмотическую составляющую скорости. Также и в [11] показано, что последняя имеет различный вид для маленьких (по сравнению с X _D и больших частиц):

дет выражение для скорости электроосмотического потока в плоской и прямоугольной щелях [77,

92-94]:

u ( z ) = V * 1 -\

Chf K z ) ^ ch( a )

, где коэффициент

пропорциональности а выражается по-разному.

Например, уравнение для скоростного профиля в плоской щели примет вид [77]

A 2E^ee0ch(X)

U (z) =-------------

Ц

= F h^C ₀ /( ££ ₀ RT )

ch( X )

где

(F, R и £ 0 — постоянные Фа

радея, газовая и электрическая, Е — напряженность электрического поля).

В [93, 94] аппроксимация скоростного профиля

уже для прямоугольного сечения в вертикальном поле (вдоль оси z ) имеет вид: U ( у , z ) =

= U ( у ) 1 -

ch( Уз z / a ) ch(V3/ a )

угольного сечения. При

где а — глубина прямо- всем отличии механизмов

формирования скоростного профиля, его аппроксимации качественно одинаковы.

Достаточно важным аспектом является невоз-

можность в большинстве случаев получить точное аналитическое решение профиля электрического потенциала и, как следствие, скоростного профиля. В то же время традиционные численные мето-

ды типа метода конечных элементов позволяют моделировать профили численно. Основная проблема, отмеченная, в частности, в работах [95, 96], состоит в сложности "склеивания" решений, поскольку двойной электрический слой многократно тоньше микроканала.

Приближенные аналитические решения, как правило, при дополнительных упрощающих пред-

положениях, можно получить на основе метода моментов. Введем моменты порядка п , определяемые как

q £ 0 E         л

= ,     , r s <<  ^X D ,

6 лц r_s

££ 0ZE         ,

Ц

Здесь r s — радиус Стокса, q — заряд частицы. Второе равенство представляет собой известное уравнение Смолуховского [90].

+^

Ц п ( z , t ) = J xⁿC ( x , z , t )d x , -^

Ц (0, t ) = 0 д Ц п (1, t ) d z       ’      d z

Данная формула содержит граничные условия 2-го рода, являющиеся следствиями непроницаемости стенок для вещества и симметричности канала (плоской щели).

(12) = 0.

Подобный метод решения — метод моментов предложен в работе [97], а решение аналогичной задачи применительно к хроматографии описано в ряде работ, например в [98] и [99]. Нетрудно убедиться, что по аналогии с теорией вероятностей [100] момент ц ₀ имеет смысл количества вещества, отношение CT = Ц 1 / ц ₀ определяет центр тяжести аналитического сигнала, его дисперсия определяется как о ² = ц 2 / ц ₀ - CT².

Уравнение (7) преобразуется для моментов (12) в нормированных параметрах к виду d t        дz2

= nu * (1 — | z|^m ) Ц п - i + ^{п ( п -} 1) D * Ц п - 2 ;         ⁽¹³⁾

п = 0,1,2,3...

Здесь D * = D / h ², u * = u / h ; h — полуширина щели, D , u — коэффициент диффузии и максимальная конвективная скорость, z — относительная координата сечения, отсчитываемая от оси ( z = = 0 на оси щели, z = 1 на стенке).

В работе [75] для описанного случая на основе рекуррентной формулы (13) получены формулы для усредненных по сечению микроканала в форме плоской щели координаты центра тяжести аналитического пика компоненты и дисперсии пика:

< CT > = u * B ⁰ 1 ,

+^ T2Jj2

2 + Pe²y B—

9( V )²

-

D * t +

э +^ — Pe² У ²     j = 1 ( n j)

.

Здесь Pe = u */ D * , A ₀ — нормированная на h длина пробы, B^j — коэффициенты разложения конвективного скоростного профиля (1– z^m ) в ряд Фурье по косинусам.

Таким образом, в большинстве работ в качестве теоретических предпосылок для описания процессов массообмена в микрофлюидных системах используют уравнение Навье—Стокса, систему уравнений Пуассона—Больцмана и ее линейное приближение Дебая—Хаскела для распределения электрического потенциала по сечению микроканала и электроосмотического потока и принцип аддитивного сложения скоростей в случае электроосмоса в сочетании с градиентом давления.

При этом очевидно, что наличие двух составляющих при формировании конвективной скорости приводит к весьма широкому разнообразию форм профиля. Поэтому собственно положение о параболическом скоростном профиле аксиаль-

ной (маршевой) составляющей конвективной скорости не только в случае ввода вещества давлением [60–62], но и при электрокинетическом вводе пробы [59, 61–63, 70], а также для достаточно сложного случая параболического потока после смешивания [64] представляется малообоснованным, несмотря на весьма широкое его признание.

Тепловые поля

До недавнего времени в литературе практически отсутствовал количественный анализ влияния температурного поля и состояния поверхности канала на процессы конвективно-диффузионного массопереноса в микроканале чипа при констатации на качественном уровне значимости указанных эффектов. Например, в работе [69] обсуждено влияние джоулева тепла на дисперсию пробы, проанализирована температуропроводность различных чиповых материалов (ПДМС, ПММА, ПК, ПЕТ, стекло), а также рассмотрено распределение температуры по сечению широкого микроканала ( h = 500 мкм). В цикле лекций [70] влияние температуры исследовано только с позиций изменения коэффициента динамической вязкости.

В последнее время появилась серия работ [65– 68, 77, 101], в которых экспериментально и методом численного моделирования изучены закономерности формирования продольных и поперечных тепловых полей и их влияние на процессы конвективно-диффузионного массопереноса.

Уравнение Навье—Стокса для температуры имеет аналогичную приведенной ранее форму с учетом замены динамической вязкости на коэффициент температуропроводности (термодиффузии), а также дополненную источниковыми слагаемыми, в частности связанными с тепловым действием электрического поля. Естественными граничными условиями являются смешанные условия второго (симметрия на оси) и третьего (ньютоновский поток на стенке) рода.

В работе [101] достаточно полно представлены зависимости, характеризующие температурное изменение базовых характеристик процесса мас-сопереноса, а именно коэффициента динамической вязкости и коэффициента диффузии. Данные по аппроксимации зависимости динамической вязкости от температуры ц = ц (Т ) приведены в [68] (см. табл. 3) и в [101]. В работе [102] эта зависимость подтверждается, в [103] данные отличаются при Т > 25 ^oC на 3 %. В общем случае можно утверждать, что ln( ц ) = 0 / T , где константа 0 может быть отлична от 1713. В табл. 5 даны другие значения коэффициента 0 .

Коэффициент диффузии также достаточно сильно меняется с изменением температуры —

это зависимость Стокса—Эйнштейна [112, 113]

kT            _*

D =-----7. Здесь d — гидродинамический диа-

3npd метр частицы. Кроме того, диэлектрическая проницаемость буфера также обладает достаточно сильной температурной зависимостью (см. табл. 3). Следовательно, как и было отмечено в [77], изменения температуры через коэффициенты в уравнениях Пуассона—Больцмана, через величину дебаевской длины влияют на профиль конвективной скорости и поперечное распределение потенциала.

Наиболее подробно базовые дифференциальные уравнения теплопереноса описаны в [68]. Рассмотрен практически реализуемый случай кругло- го микрокапилляра, стеклянная стенка и внешнее термоизолирующее покрытие.

Уравнения примут вид:

— для теплопереноса в микрокапилляре

— для теплопереноса в стеклянной стенке и в покрытии

P C P d T = V- [ **(T) V T ] . d t

Соответственно для стенки и термозащитного покрытия будут различные плотности р , удельные изобарические теплоемкости С р ^* и температурные зависимости коэффициента температуропроводности или термодиффузии. Изменение температуры в микрокапилляре зависит от конвективного потока тепла v - V T и от внешнего источника тепла, связанного с электрическим полем, Х (t ) C E - E , где С — концентрация водоподобного буфера, E = { E aks , E rad } — вектор напряженности электрического поля. Т. е. помимо конвективного и термодиффузионного массопереноса, в микроканале имеется источник тепла — тепловое действие электрического поля. Вместе с тем граничное условие связано с ньютоновским потоком через стеклянную стенку, обеспечивающим частичный отвод тепла (см. раздел "Граничные условия на стенках микроканалов"). В работе [68] подробно

Табл. 5. Значения температурного коэффициента 6 в аппроксимации ln( ц ) = 6 * + 6 / T

Величина 6 Публикация 1820 [104] 2400 [105–108] 2040 [109] 2234 [110] 1600 [111] описан метод обезразмеривания уравнений и некоторые численно полученные решения.

Нетрудно заметить, что уравнение теплопере-носа в микроканале отличается от уравнений для стеклянной стенки и покрытия. Однако все они являются аналогами уравнения Навье—Стокса.

Следует отметить существенную особенность, связанную со вкладами продольной (аксиальной Е aks ) и поперечной ( Е rad ) составляющих электрического поля. Типичными значениями напряженности управляющего (продольного) электрического поля при электрокинетическом управлении являются 10–20 кВ/м, в отдельных случаях до 75 кВ/м [68] и 5–15 кВ/м [66]. Также отмечено, что на отдельных стадиях анализа напряженность продольного электрического поля не превосходит 200 В/см [11]. Большинство анализов в [72–74, 76] проводилось при напряженностях продольного электрического поля от 150 до 500 В/см. Т. е. характерным масштабом напряженности электрического поля является 10⁴ В/м. Вклад поперечного электрического поля можно оценить косвенно, основываясь на уравнении Пуассона—Больцмана. Поскольку потенциал на оси микроканала может быть достаточно близок к нулю, а на стенке он равен дзета-потенциалу, то приближенной оценкой напряженности электрического поля можно считать E_rad ~ Z / r , где r — радиус (или полуширина) канала. Величина дзета-потенциала имеет порядок 10–100 мВ (10^–2–10^–1 В), типичная полуширина микроканала — 10^–5–10^–4 м (10–100 мкм). Следовательно, E rad = 10²–10⁴ В/м, и эта составляющая может быть соизмерима с продольной. При этом методы управления составляющими электрического поля принципиально разные. Продольное поле регулируется выбором управляющих потенциалов; для поперечного поля требуется управление (модификация) поверхности канала с подбором величины дзета-потенциала. Кроме того, поперечное распределение потенциала еще зависит от температуры.

Модель жидкости

Характер жидкости в значительной степени определяется характеристическим числом Шмидта Sc = ^—. Принято считать, что для водоподобных

PD жидкостей это число порядка 1000. В частности, в работе [114] принято 2450. Кроме того, кинематическая вязкость v = ц / р имеет порядок 10–2 см2/с.

Более существенным является разделение на ньютоновские и неньютоновские жидкости. Для ньютоновских жидкостей динамическая вязкость не зависит от режима движения, но при этом существенно зависит от температуры. Неньютонов- ские жидкости еще называют аномально-вязкими или структурно-вязкими. К таким жидкостям относятся, в частности, суспензии, эмульсии, растворы и расплавы полимеров и т. п. Их динамическая вязкость зависит от характера движения, т. е. µ = µ(Re) даже для малых чисел Рейнольдса (при ламинарном движении).

Типичными неньютоновскими жидкостями являются растворы полимеров. Зависимости их физико-химических характеристик, в том числе и вязкости, от концентрации полимеров и других параметров рассматриваются в работах [57, 58, 115–117]. Примерный метод расчета вязкости суспензии при допущении сферической формы частиц дан, например, в [118]. Там же поясняется, что оценивание коэффициента динамической вязкости при произвольной симметричной форме частиц связано со значительными вычислительными трудностями, поскольку требует использования тензора напряжений. В целом неньютоновские свойства жидкости приведут к существенному усложнению уравнений и граничных условий. Эти жидкости являются предметом реологии. Некоторые из реологических моделей растворов полимеров представлены в [57, 58].

Одной из удобных реологических моделей является модель степенной жидкости Оствальда— де Виля, хорошо зарекомендовавшая себя на практике. Она характеризуется двумя параметрами: m (консистентность смеси), N (параметр неньютоно-вости). N определяет отклонение от ньютоновской жидкости (для воды N =1, для концентрированной суспензии N больше 1, а для полимеров N — меньше 1). При таком подходе связь между касательными напряжениями τ в среде и скоростью конвективного движения имеет вид

∂ u ∂ u τ ≅ m

∂ z ∂ z

N - 1

Следовательно, уравнение Навье—Стокса изменит форму вязкого слагаемого, которое станет 1 ∂     ∂τ функцией N, U(z) и m, а именно ⋅   (y ) .

y^k ∂ y    ∂ y

Здесь y — поперечная пространственная координата, k = 0,1,2 для декартовых, цилиндрических и сферических координат соответственно. Рассмотренный ранее случай предполагал ньютоновскую водоподобную жидкость ( N = 1) и постоянную величину динамической вязкости ( m = µ ).

Видно, что реологическая модель жидкости содержит на один параметр больше, чем ньютоновская. Таким образом, выбор режима анализа с неньютоновской средой разделения имеет большее число степеней свободы (управляющих параметров), что дает дополнительные возможности оптимизации.

ВЫВОДЫ

Анализ теоретических положений, лежащих в основе разработки микрофлюидных аналитических систем, позволяет утверждать:

— Реализованные варианты анализов на микрочипах не ограничиваются режимами ламинарных потоков. Прежде всего это относится к системам не с электрокинетическим вводом, а с вводом вещества давлением.

— Практически во всех случаях гипотеза сплошной среды обоснована.

— Уравнения массопереноса базируются на системе уравнений Навье—Стокса. Профиль конвективной скорости должен быть отличен от параболического, поскольку требуется учет электроосмотического потока. Граничное условие на жесткой стенке при этом состоит в непроницаемости последней для вещества. Условия, связанные с конвективной скоростью могут быть различными.

— Электроосмотический поток описывается системой дифференциальных уравнений Пуассона—Больцмана, включающей в себя уравнения для электрического потенциала и теплопереноса. Характерный геометрический параметр — толщина двойного электрического слоя — связан с дебаевской величиной и составляет порядка 10–100 нм и весьма мал по сравнению с характерным размером сечения микроканала. Последнее обстоятельство приводит к вычислительным осложнениям, поскольку требуется стыковать различные решения на несоизмеримых по толщине слоях.

— Дифференциальное уравнение для теплопе-реноса в микроканале по форме напоминает концентрационное уравнение Навье—Стокса при необходимой замене переменных на их аналоги. Существенными являются две особенности: а) наличие источникового слагаемого, связанного как с продольным, так и с поперечным электрическими полями; б) граничное условие третьего рода на стенке в форме ньютоновского потока.

— Модели неньютоновских жидкостей в качестве буфера и разделительной среды требуют использования реологических моделей, что приводит к потере линейности вязкого слагаемого в уравнении Навье—Стокса, но позволяет использовать реологический показатель как управляющий параметр для оптимизации процесса анализа.