Математическое моделирование в управлении персоналом

Принятие решений является важной частью процесса управления организацией. Руководитель, принимающий управленческие решения, не может полагаться только на свой опыт и интуицию, он должен обладать профессиональными знаниями, владеть приемами и методами принятия решений, навыками работы с людьми.

Результативность работы группы людей или организации во многом зависит от управленческой деятельности руководителя. Подготовка управленческих решений в современных организациях предусматривает работу целого коллектива специалистов, которые будут реализовывать эти решения. Таким образом, одной из важнейших задач руководителя является подбор высококвалифицированных, инициативных специалистов, способных эффективно работать в команде. Процесс принятия обоснованных объективных решений в подобных ситуациях достигается путем использования научного подхода к данному процессу, математических моделей и количественных методов принятия решений.

Решение задач управления персоналом с помощью математических методов требует учета множества факторов, различных по важности, таких как создание психологического климата в коллективе, отбор кандидатов и назначение их на должности, соответствующие их уровню профессиональной подготовки, интеллекту, способностям. Как правило, прием на работу в организацию руководитель или соответствующие службы осуществляют на основании резюме и собеседования с претендентом на должность, а также собственной интуиции. В результате каждый конкретный кандидат назначается на конкретную должность, то есть решается задача о назначениях.

Рассмотрим математическую модель задачи о назначениях [1], позволяющую получить оптимальное назначение, то есть назначить n кандидатов на n вакантных должностей, с целью получения наилучшего эффекта от работы группы.

Математическая модель задачи заключается в нахождении оптимального значения (min или max) целевой функции

L ( X ) = L ILc y x y ^ min ^(max)

i = 1 j = 1

при следующих ограничениях:

n

L x , = 1, i = 1, n ; j:'       _

• • L x , = ', j = ', n ;

_; = ' x_y = 0 или 1.

где х ij = 0 , если i -ый кандидат не назначается на j -ую должность, и х ij = 1 , в противном случае. Элементами c ij матрицы C могут быть время выполнения задания работниками, тогда решается задача на min, доход организации от выполненных работ, рейтинги кандидатов на должности, тогда решается задача на max.

Алгоритм решения задачи рассмотрим на конкретном примере: пять кандидатов (А 1 , А 2 , А 3 , A 4 , A 5 ) претендуют на должности (В 1 , В 2 , В 3 , B 4 , B 5 ), соответствующие определенным профессиональным типам деятельности. Для каждого кандидата рассчитан рейтинг по методике профессиональных предпочтений Дж. Голланда [2], позволяющей соотнести склонности, способности, уровень интеллекта человека с различными профессиями. Суть теории Дж. Голланда в том, что успешная профессиональная деятельность зависит от типа личности и типа профессиональной среды, которая способствует раскрытию способностей человека, желанию работать в коллективе с максимальной эффективностью.

Используя опросник профессиональных предпочтений Дж. Голланда [3], была сформирована матрица C рейтингов претендентов на должности по принадлежности и максимальной полезности выполнения определенного типа работы, соотносительно с типом направленности личности. Строки матрицы – кандидаты на должности, столбцы – должности. Требуется назначить кандидатов на должности, обеспечив максимальный профессиональный рейтинг команды, то есть решить задачу на максимум. Применим венгерский метод для решения задачи о назначениях [1].

Произведем преобразование матрицы C, Г 7 6 6 8 7 3 5 9 7 6 8 С = 6 8 10 4 10 8 9 9 3 5 15 7 8 8 7 J умножим ее элементы на (-1) и сложим каждый элемент полученной матрицы с положительным числом (в нашем случае это число 11), так чтобы новая матрица содержала только неотрицательные элементы. Получим следующую матрицу:

Г4  5  5  34

6  2  4  53

5   3   1   71

3  2  2  86

v6  4  3  34

Из каждой строки и каждого столбца матрицы вычитаем соответствующий минимальный элемент, с целью получения наибольшего количества нулевых элементов в матрице C.

Значения минимальных элементов строк матрицы равны 3, 2, 1, 2, 3 соответственно. Вычитая из элементов каждой строки соответствующее минимальное значение, получим:

Г1  2  2  01

4  0  2  31

4  2  0  60

1  0  0  64

v 3  10  01

Значения минимальных элементов столбцов матрицы равны 1, 0, 0, 0, 0 соответственно. Вычитая из элементов каждого столбца соответствующее минимальное значение, получим:

Г0  2  2  01

• 3  0  2  31

• 3  2  0  60

0  0  0  64

_v 2 10 0 1 _v

Так как ни одно полное назначение не получено, то есть нельзя выбрать в каждой строке и каждом столбце по одному единственному нулевому элементу, то необходимо провести модификацию матрицы, с целью получения допустимого решения.

Проводим прямые через отдельные строки и столбцы матрицы, чтобы все нулевые элементы были вычеркнуты. Вычеркиваем 1-ую, 3-ю, 4-ую, 5ую строки и 2-й столбец, Из оставшихся не вычеркнутыми элементов выбираем минимальный, равный 1.

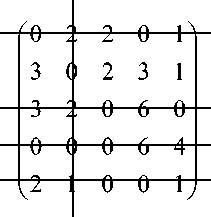
Вычитаем его из всех не вычеркнутых элементов и, прибавляем ко всем элементам, расположенным на пересечении прямых, получим следующую матрицу. Выбираем по одному единственному нулевому элементу в каждой строке и каждом столбце матрицы:

Г0  3  2  0  1

• 2 0 120

• 3  3  0  60

0 10 64

• v 2  2  0  0   1

Заменим в полученной матрице выбранные элементы единицами, а остальные элементы нулями и запишем оптимальное назначение:

^0  0  0  10

0 10 00

X опт

0  0  0  01

1  0  0  00

v0  0  1  00

Таким образом, кандидат A 1 назначается на должность B 4 , A 2 назначается на должность B 2 , A 3 – на B 5 , A 4 – на B 1 , A 5 – на B 3 . Суммарный рейтинг всей команды составляет 8+9+10+8+8 = 43. Используя венгерский алгоритм решения задачи о назначении, найден оптимальный вариант по подбору персонала на вакантные должности.