Математическое моделирование волны термоядерного горения, инициированной сферическим игнитором в мишенях инерциального термоядерного синтеза

Управляемый термоядерный синтез (УТС) привлекателен многими аспектами, но один из самых важных для практического применения — это неисчерпаемость термоядерного топлива на нашей планете. В качестве топлива можно использовать тяжелые изотопы водорода, например, дейтерий.

В [1] сделаны оценки минимальной энергии лазерного импульса с учётом тепловыделения. Из этих оценок следует, что для термоядерного синтеза (ТС) выгоднее всего использовать DT-плазму, сжатую до высоких плотностей, многократно превышающих плотность твёрдого водорода.

В статье [2] был сформулирован подход быстрого зажигания (fast ignition) мишени. Вещество мишени сначала сжимается длинным лазерным импульсом до большой плотности при относительно малой температуре. Затем небольшая часть сжатого вещества быстро нагревается до необходимой для зажигания температуры. В рамках концепции fast ignition зажигание предполагалось осуществить на конечной стадии сжатия с помощью релятивистских электронов, ускоренных пе-таваттным лазерным импульсом (третьим по счету) в плотном веществе внутри мишени, куда лазерное излучение должно было проникнуть, распространяясь внутри канала, созданного вторым лазерным импульсом.

В данной работе расcматривается двухстадийный механизм инициирования волны термоядерного (ТЯ) горения в мишенях лазерного термоядерного синтеза (ЛТС). Этот процесс протекает следующим образом: на первом этапе формируется область высокоплотной, но относительно холодной плазмы, на втором этапе внутри этой области при помощи дополнительного энергетического импульса образуется высокотемпературная подобласть, называемая игнитором. Для реализации второго этапа — создание игнитора — существует несколько вариантов: во-первых, при помощи потока быстрых электронов, образующих- ся при воздействии на вещество лазерного излучения; во-вторых, используя пучки многозарядных ионов, или с помощью протонов, ускоренных лазерным импульсом релятивистской интенсивности в специальной мишени, расположенной в непосредственной близости от ТЯ мишени. При реализации любого из перечисленных методов быстрого поджига возникает одна существенная проблема: форма игнитора и основной плазмы мишени перестает быть сферически симметричной, что может сказаться на эффективности выгорания ТЯ топлива, в частности, увеличить критическую энергию игнитора, необходимую для поджига мишени. Приведённая выше модель инициирования позволяет существенно снизить требования к профилированию и стабильности основного лазерного импульса, при этом коэффициент усиления мишени может не претерпевать особых изменений.

При исследовании процесса ТЯ горения мишени определённый интерес представляют физические явления, происходящие на начальной стадии в высокотемпературной плотной плазме.

Представленная работа связана с разработкой и тестированием пакета программ, моделирующего ТЯ процесс горения в сферически симметричном случае. В частности, изучаются физические процессы, протекающие в разные моменты времени как на самой ранней стадии, так и на более поздней. Осуществлено сравнение аналитического решения с результатами численного моделирования, исследована сходимость численных решений при измельчении сетки.

• II.    Математическая модель

Рассматривается осесимметричная задача ТЯ горения плотной высокотемпературной дейтери-ево-тритиевой плазмы. Используется гидродинамическое одножидкостное двухтемпературное приближение, включающее процессы электронной и ионной теплопроводности, электрон-ионной столкновительной релаксации и выделение энергии за счёт ТЯ реакций.

82                  Прикладная физика ТРУДЫ МФТИ. — 2010. — Том 2, № 3 Для описания ТЯ горения плазмы в переменных Эйлера (r; θ) сферической системы координат выбрана следующая математическая модель, которая имеет следующий вид: lnAf = ln[1 + 5,27 • (0,39 + 51 • Ti/(p)1 /3]; ki = 2,51967 • 1018 • (Ti)5/2/In Ai [----эрг— ]; см с кэВ In Ai = 0,5ln[1 + 4,3993 • 104 • Ti3/p]; др 1 д (r2 pU)      1 д (sin 9pV) дt ' r2    dr ' r sin 9     д9          , Qei — коэффициент электронно-ионного обмена: Qei = 2,815 • 1024 x дpU 1 д [ r2 (pU2 + P)]     1  д (sin 9p UV) де    r2       dr        ' r sin 9     д9 p2 • ln[1 + 3,59 • 104 • (Te2 + 8,862 • 10-5 • p4/3)/p] = T’                (2) Te3/2 + 1,262 • 10-3p [     эрг     ]; дpV 1 д (r 2 pUV)     1  д [sin 9 (pV 2 + P)] дt    r2    дr     ' r sin 9        д9 см3 с кэВ QТ.Я — энерговыделение за счёт ТЯ реакций: = cos 9P r sin 9 , QТ.Я = 8,483 • 1029 x 2 (1 + 0,232 • Ti3/4)exp(-20/Ti1 /3) эрг дрЕ 1 д [ r2 U (pE + P)] дt + r 2      дr      + X p                 /                                      [ з ]; Ti2/3 • 1 + 9,41 • 10- 5 • Ti13/4 см • с 1  д [sin 9V (pE + P)] + r sin 9       д9        = QТ • Я+ [Ti] — кэВ; [Te] — кэВ; [p] — г/см3. Исходная система уравнений включает уравнение + £ д [ r 2( We }r ] +   1   д [sin 9 (We) e ] + r2     дr       r sin 9     д9 неразрывности вещества (1), законы количества движения (2)--(3) (для радиальной и тангенциаль- + £ д [ r2 (Wi }r ] +   1   д [sin 9 (Wi) e]     (4) r2     дr        r sin 9      д9     , ной компоненты импульса соответственно), законы сохранения для полной энергии (4) и изменение ионной составляющей плазмы (5). дpei 1 д (r2 Upei)      1 д (sin 9V pei) дt    r2    дr     ' r sin 9     д9 В физической модели предполагается, что энергия α-частиц локально передаётся электрон- P [1 д(r2 U)      1   д(sin 9V)] + i r2   дr ' r sin 9 д9 ной составляющей плазмы, а нейтроны не взаимодействуют с веществом мишени и свободно её покидают. _ Q .(T —T-) + X д[r2(Wi}r] ।    1 д[sin9(Wi)e] ei e i r2     дr        r sin 9      д9      , (5) где ρ — плотность; U — радиальная r-компонента скорости; V — тангенциальная θ-компонента скорости; εi — ионная удельная внутренняя энергия; εe — электронная удельная внутренняя энергия; E = ee + ei + (U2 + V2) / 2 — полная удельная энергия; P = (y — 1)p(ee + ei) — давление; y = 5/3 — показатель адиабаты; Pi = (y — 1)pei — ионное давление; We,i — тепловые потоки за счёт электронной и ионной теплопроводности: Используемая на первом полушаге схема расчёта предполагает, что гидродинамическая часть уравнения, имеющая гиперболический тип, аппроксимируется явно. Рассматривается двухмерный случай и используется явная схема первого порядка точности, для которой выполняется условие Куранта–Фридрихса–Леви. Вместе с гидродинамикой учитывается ТЯ выход. В результате мы получаем окончательное значение плотности, компоненты вектора скорости и предварительные значения электронной и ионной температур. На следующем полушаге производится учёт членов WWe = ke grad Te, с электронной и ионной теплопроводностью по неявной схеме (схема пространственного покомпо- WWi = ki grad Ti, нентного расщепления с итерациями по нелинейным коэффицентам электронной и ионной тепло- где Te ,Ti — соответственно электронная и ионная температуры; проводности). В итоге, учитывая граничные условия для электронной и ионной температур, по- ke = У k 2 + k 2; лучаем краевую разностную задачу относительно них, которая решается итерациями с использованием одномерных прогонок по лучам. На третьем k = 9,83 • 1019 • T5/2 [    эрг ] 1          1пЛ ei       см • с • кэВ , полушаге учитывается электронно-ионная релаксация. k = 2,54716 • 1017 • p • Te [ эрг ] 2           In ЛF         см • с • кэВ , III. Постановка задачи В данной работе рассматривается ТЯ горение ln Л ei = 0,5 ln[1 + 3,59 • 104 • T? + 8862 • 10 - 5 p4 /3 ]; ρ специальной сферически семметричной мишени. В ее центральной части, состоящей из плотной плазмы, создают область повышенной температуры (см. введение). На рис. 1 представлена структура расчётной области. Игнитор — это сфера наименьшего радиуса 35 мкм, в которой находится горячая и плотная плазма. Следующая область, имеющая форму шарового слоя с внутренним радиусом 35 мкм и внешним 300 мкм, — плотная и холодная плазма, занимающая большую часть мишени. Пространство между границами мишени и границей расчётной области заполнено относительно холодной и разреженной плазмой.

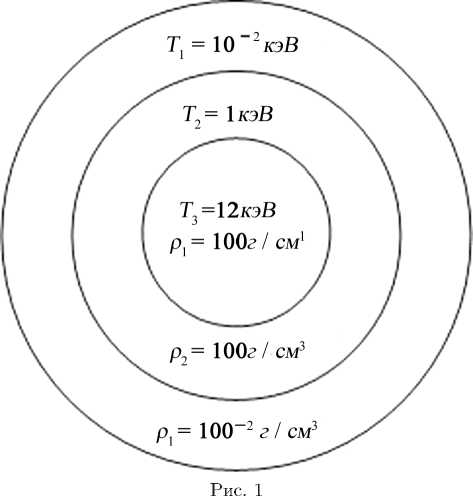
В качестве модельной задачи для отладки первого этапа разностной схемы, на котором учитывается гидродинамика, выбран случай гидродинамического распада разрыва с образованием волны сжатия и волны разрежения.

В начальный момент времени наблюдаем разрыв на расстоянии 35 мкм от центра мишени — граница игнитора. В игниторе температура 12 кэВ, за его границей и до конца мишени — 1 кэВ. Мы наблюдаем распад разрыва с образованием ударной волны и волны сжатия (рис. 2).

На ударной волне должны выполняться три основных закона сохранения: массы, количества движения и энергии. Запишем соотношения Рэн-кина–Гюгонио, отражающие эти законы:

Р 1(U1 — Dо) = Ро(Uо — Dо),

P1 + Рi(U1 - Dо)2 = Pо + Ро(Uо - Dо)2,

(Ui — D о) {р 1[е 1+ -—2—~ ]+ P1 ^ =

= (Uо — D о) {Ро[ ео +  ---2—~ 1 + Pо }■

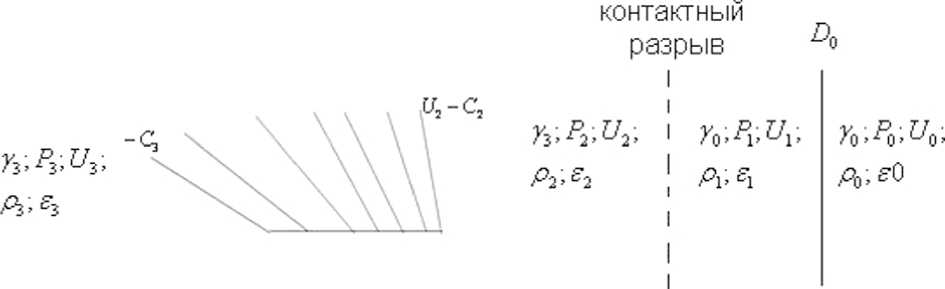
На контактной границе скорость и давление связаны следующими соотношениями:

U1 = U2,    P1 = P2.

Воспользуемся аналитическим решением вспомогательной задачи. Аналитическое решение полной задачи, состоящей из системы нелинейных уравнений, в настоящее время получить затруднительно, поэтому отладка программы проводится на модельной задаче, для которой существует

В волне разрежения сохраняются значения инварианта на характеристике U + C :

Uз +

2C3

γ3

1

= U2 +

2C2

Y3 -

1 ^,

аналитическое решение.

• IV.    Сравнение аналитического и численных решений на модельной задаче

где C 3 и C 2 — скорость звука в игниторе и в обла сти постоянного течения между волной разреже ния и контактной границей соответственно.

При помощи этих соотношений строим харак теристики U + C в волне разрежения.

Закон сохранения массы выполняется для сеток с разным количеством узлов с различной степенью точности. Радиус расчётной области в модельной задаче составляет 60 мкм. Масса, распределенная по сфере этого радиуса:

V = 4 • п • 0,63/3 = 0,90478 • 10“6 см3,

m = V • 100 г/см3 = 90,478 • 10“6 г.

Численное моделирование для равномерных сеток с различными шагами точности дало следующее распределение массы: 500 узлов на каждый луч, всего 4 луча — 78 , 78651 • 10 ^{_ 6} г, 1000 узлов на каждый луч, всего 8 лучей — 87 , 25661 • 10 ^{_ 6} г, 2000 узлов на каждый луч, всего 16 лучей — 89 , 31799 • 10 ^{_ 6} г, 4000 узлов на каждый луч, всего 32 луча — 89 , 99397 • 10 ^{_ 6} г. В результате математических преобразований [6] получаем уравнение для z = Р 1 /Р з :

X 2 Z 2 n - а 0 v 2 XZ n+2 + 2 а 0 v (ц + v) XZn+1 -

- [2 + (ц + v )2 а о ] XZn - v2 Z2 + 2 v (ц + v) Z - n = 5, v2 = 60

получаем алгебраическое уравнеие 10-й степени:

144 z10 - 2880z7+5760z6-2904z 5 - 60 z 2+120 z-59 = 0.

(6)

При решении уравнения (6) получаем 10 корней, из которых 8 корней являются комплексными, а из оставшихся один корень положительный. Найденное решение:

Pi/Рз = z = 0,8707787311, где Pз — давление в игниторе, а Р1 = 4,639• 1017 дин/см2 давление в области постоянного течения между контактным разрывом и ударной волной. Затем находим скорость распространения ударной волны:

D0 = 8,027 • 107 см/с, скорости перемещения контактного разрыва и плотности в областях постоянного течения:

U1 = 4,818 • 107 см/с,

— (ц + v )2 + 1 — 0.

U 1 = U 2 ,

После подстановки числовых значений:

р 1 = 250 , 181 г / см ³ ,

Yз = Y о = 3, Ц = 0, а 0 = 4, X2 = 144,

р2 = 66,027 г/см3.

Сравнение результатов представлено на рис. 3, 4, 5.

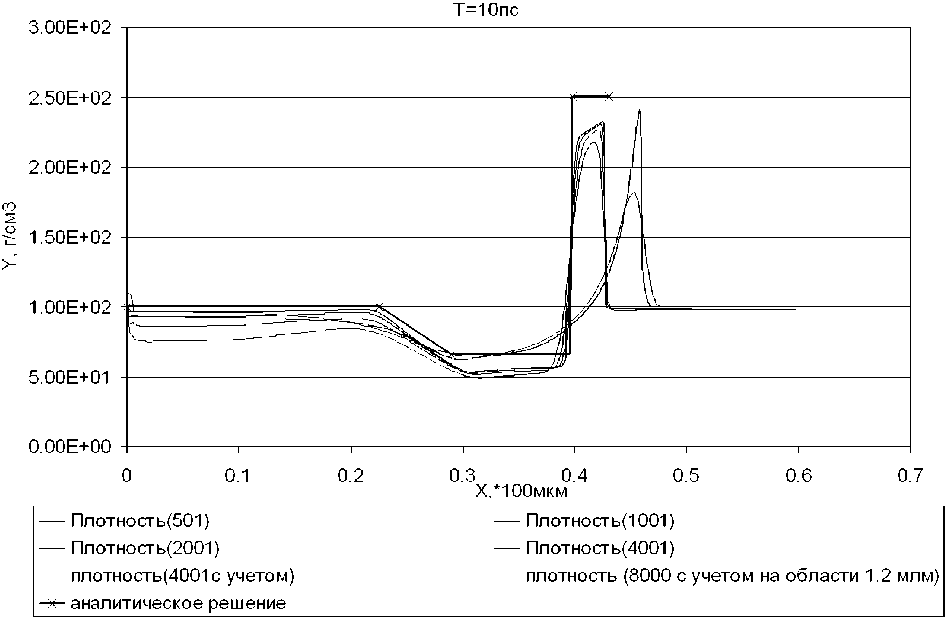
Рис. 3

Давление(501)                          —Давление(1001)

Давление(2001)                         —Давление(4001)

Давление(4001 с учетом)                 —Аналитическое решение давление (8000 с учетом на области 1,2млм)

Рис. 4

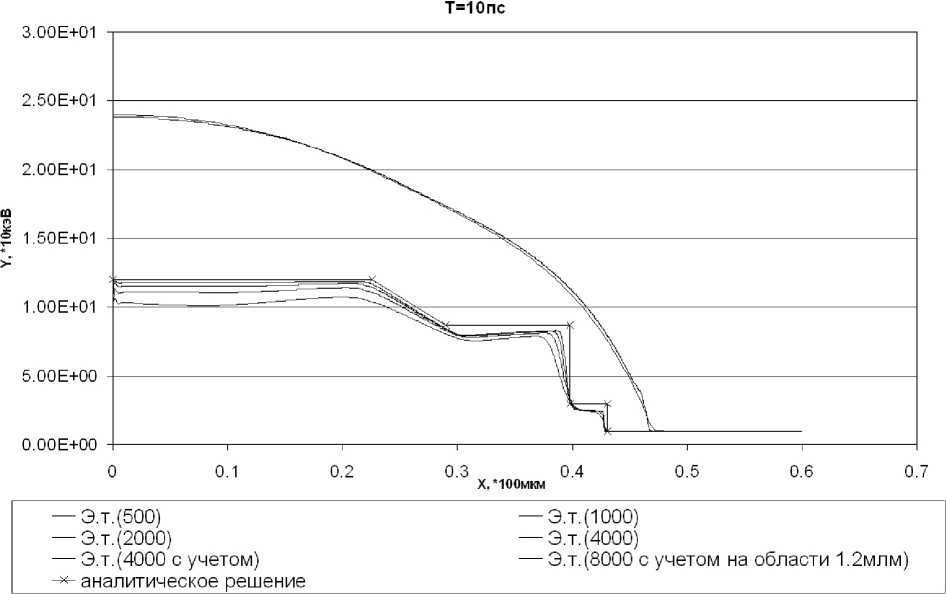
На рис. 3 показано распределение плотности по радиальному направлению. «Плотность (501)», «плотность (1001)», «плотность (2001)», «плотность (4001)» — результаты численного моделирования модельной гидродинамической задачи на области 60 мкм для четырёх сеток с разным шагом. Самый нижний график — результат моделирования при использовании сетки с 500 узлами, для следующего графика использовалась сетка с 1000 узлами, затем представлен график для сетки с 2000 узлов, график, больше всех приближающийся к аналитическому решению, получен на сетке с количеством узлов 4000. Также на рис. 3 показано распределение плотности для ре-шеня полной задачи с учётом ТЯ выхода с применением сетки в 4000 узлов на области 60 мкм — «плотность (4001 с учётом)». «Плотность (8000 с учётом на области 1 , 2 мм)» — график плотности для задачи с учётом ТЯ выхода, решаемой на области 1 , 2 мм, число узлов применяемой сетки — 8000. «Аналитическое решение» — результаты аналитического решения, полученные в п. 4, где от 0 • 100 мкм до 0 , 225 • 100 мкм — невозмущённая область, в точке абсциссы 0, 225 · 100 мкм голова волны разрежения, в 0, 29 · 100 мкм — её хвост, [0 , 29; 0 , 395) • 100 мкм — область постоянного течения, в точке 0 , 395 • 100 мкм — контактный разрыв, далее следует область постоянного течения (0 , 395; 0 , 43) • 100 мкм, 0, 43 • 100 мкм — ударная волна, распространяющаяся вправо.

На рис. 4 нарисовано распределение давления по радиальному направлению. Здесь представлены четыре результата численного моделирования модельной гидродинамической задачи на области 60 мкм — «Давление (501)», «Давление (1001)», «Давление (2001)», «Давление (4001)». Самый нижний график — результат моделирования при использовании сетки с 500 узлами, для следующего графика использовалась сетка с 1000 узлами, далее — сетка с 2000 узлов, график, больше всех приближающийся к аналитическому решению, получен для сетки с числом узлов 4000. При сравнении данных, полученных при использовании различных сеток, выяснилось, что точность решения (обусловленная его приближением к аналитическому) возрастает в два раза при увеличении количества узлов в два раза. Также на рис. 4 показано распределение давления для ре-шеня полной задачи с учётом ТЯ выхода с применением сетки в 4000 узлов на области 60 мкм — «Давление (4001 с учётом)». «давление (8000 с учётом на области 1,2 млм)» — график давления для задачи с учётом ТЯ выхода, решаемой на области 1,2 млм, число узлов применяемой сетки — 8000. «Аналитическо решение» — результаты аналитического решения, полученые в п. 4, где от 0 • 100 мкм до 0,225 • 100 мкм — невозмущённая область, в точке абcциссы 0,225 • 100 мкм голова волны разрежения, в 0,29 • 100 мкм — её хвост, [0, 29; 0,395) • 100 мкм — область постоянного течения, в точке 0, 395 · 100 мкм — контактный раз- рыв, далее следует область постоянного течения (0,395; 0,43) • 100 мкм, 0,43 • 100 мкм — ударная волна, распространяющаяся вправо.

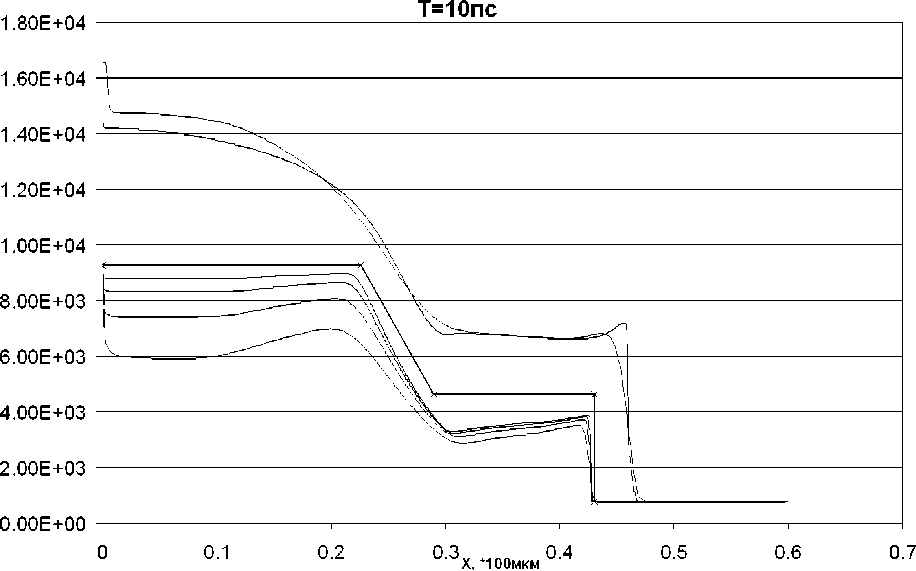
На рис. 5 изображено распределение электронной температуры по радиальному направлению. Здесь представлены четыре результата численного моделирования модельной гидродинамической задачи на области 60 мкм — «500», «1000», «2000», «4000». Соответствие графиков и используемых сеток такое же, как и на предыдущих рисунках. При сравнении данных, полученных при использовании различных сеток, выяснилось, что точность решения (обусловленная его приближением к аналитическому решению) возрастает в два раза при увеличении количества узлов в два раза. «4001 (с учётом)» — распределение давления для решеня полной задачи с учётом ТЯ выхода с применением сетки в 4000 узлов на области 60 мкм. «8000 (с учётом на области 1 , 2 мм)» — график температуры для задачи с учётом ТЯ выхода, решаемой на области 1 , 2 млм, число узлов сетки — 8000. «Аналитическое решение» — результаты аналитического решения, полученные в п. 4.

Из графиков видно, что схема действительно первого порядка точности, так как при двукратном увеличении количества узлов на той же расчётной области точность возрастает в два раза.

• V.    Результаты численного моделирования полной задачи

При развитии ТЯ горения в мишени создаются необходимые условия для возникновения детонационной волны. Во-первых, это происходит за счёт повышения плотности за фронтом ударной волны. Во-вторых, при торможении а -частиц происходит разогрев электронной компоненты плазмы (кулоновское взаимодействие), а за счёт эле-тронно-ионной релаксации происходит нагрев ионной компоненты.

На 17 , 5 пс тепловая волна входит в волну сжатия (в область постоянного течения за фронтом ударной волны) и начинает разогревать плазму за фронтом ударной волны, усилилась ТЯ реакция, в результате чего повышается давление, сформировалась ударная волна — это подтверждает максимальное энерговыделение (рис. 6). Волна сжатия сильно ослабляется тепловой волной, опережающей её.

На 22 , 5 пс наблюдаем два максимума у графика плотности: первый максимум — это результат действия ослабленной волны сжатия (максимум едва сместился в направлении от центра иг-нитора), его значение уменьшилось; второй максимум — результат действия детонационной волны. Наблюдаем начало процесса переноса вещества по направлению к центру игнитора — появился локальный максимум у графика скорости, этот максимум находится под первым максимумом плотности (рис. 7).

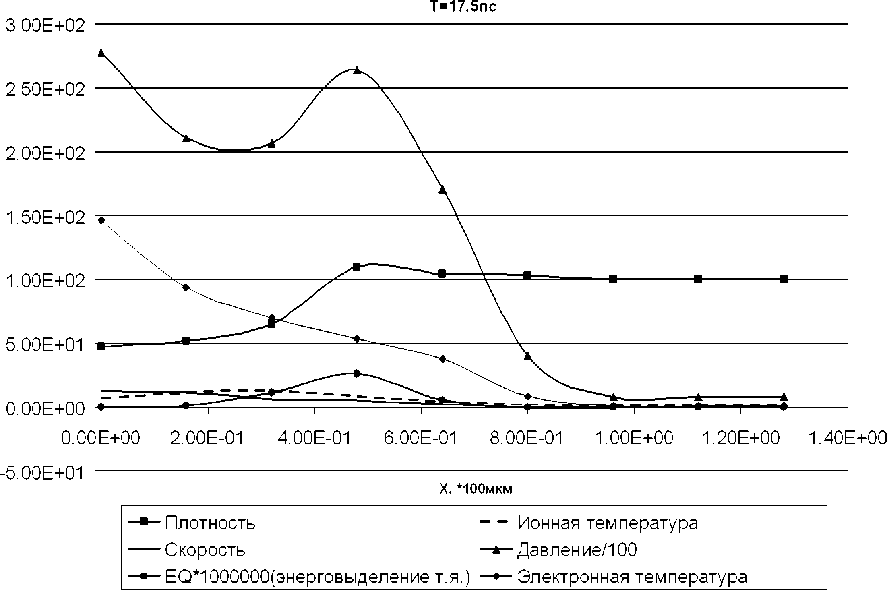
Рис. 6. Представлены графики на момент времени 17 , 5 пс. «Плотность» — по оси ординат плотность в единицах г / см ³ . «Скорость» — радиальная скорость распространения вещества в 10 7 см / с. «EQ*1 000 000 (энерговыделение ТЯ)» — энерговыделение ТЯ горения, умноженное на 10 ⁶ для соблюдения масштаба, в 10 14 кэВ / см ³ . ««Ионная температура» — температура ионов плазмы в кэВ. ««Электронная температура» — температура электронов плазмы, в кэВ. «Давление / 100 » — давление в плазме, деленное на 100 в 10 ¹⁶ дин / см 2

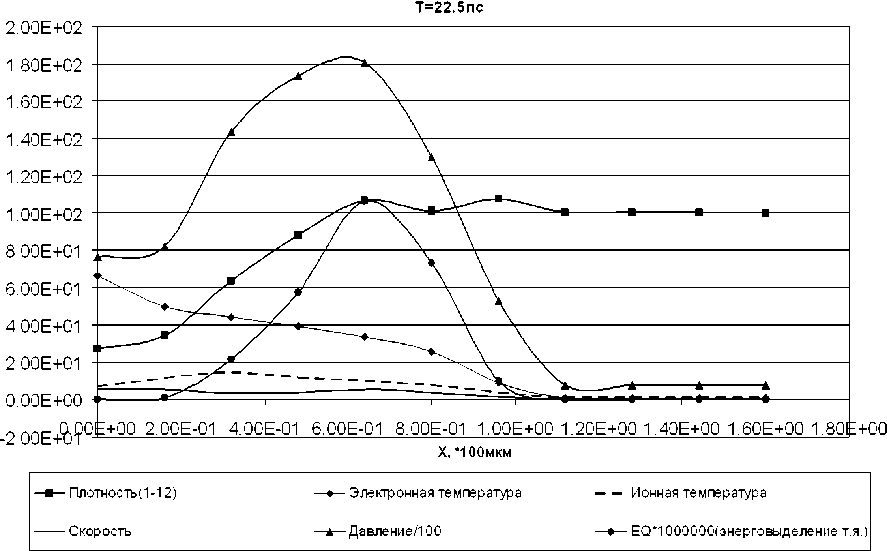
Рис. 7. Представлены графики на момент времени 22 , 5 пс. «Плотность» — по оси ординат отложена плотность в единицах г / см ³ . «Скорость» — радиальная скорость распространения вещества в 10 7 см / с. «EQ*1 000 000 (энерговыделение ТЯ)» — энерговыделение ТЯ горения, умноженное на 10 ⁶ для соблюдения масштаба, в 10 14 кэВ / см ³ . ««Ионная температура» — температура ионов плазмы в кэВ. «Электронная температура» — температура электронов плазмы, в кэВ. «Давление / 100 » — давление в плазме, деленное на 100 в 10 ¹⁶ дин / см ²

Нейтронный выход

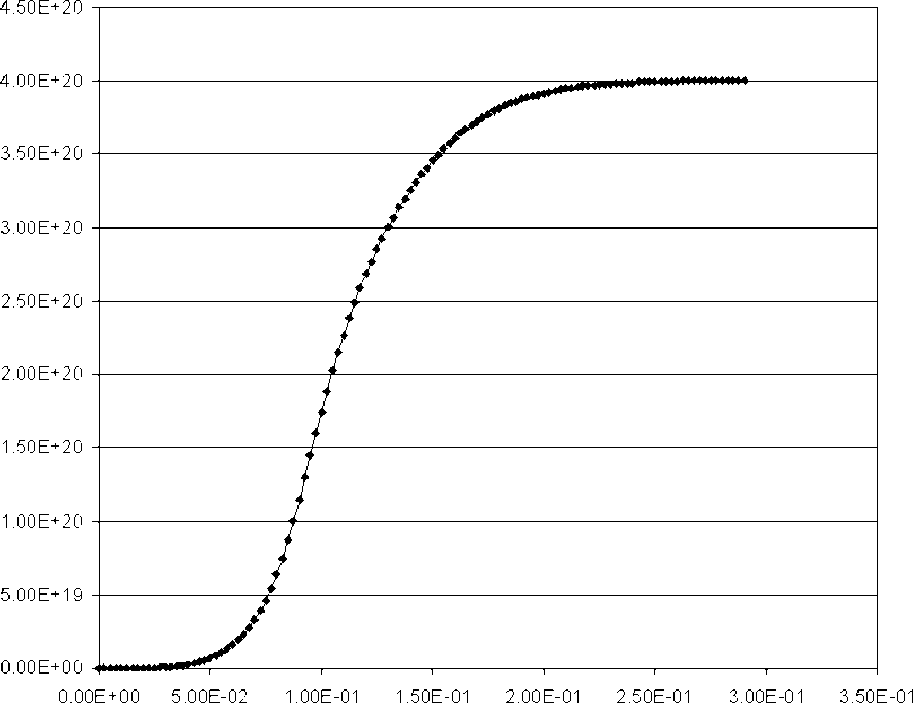
Рис. 8. Нейтронный выход по прошествии 300 пс

t, нс

На 37 , 5 пс детонационная волна сошлась в центре игнитора, её энергия перешла в кинетическую энергию ударной волны и началось сильное удельное энерговыделение — от центра начала распространяться новая ударная волна. Этот процесс из-за малых объёмов в центре мишени мало влияет на ход ТЯ реакции. Реакция поддерживается за счёт повышенного давления за фронтом детонационной волны и ионной теплопроводимости. На рис. 8 показан выход ТЯ реакции.

• VI.    Заключение

• 1.    В результате сравнения аналитического и численного решений модельной задачи, проведённого в п. 4, было установлено, что:

• 1)    схема имеет заявленный первый порядок аппроксимации;

• 2)    утечка массы незначительна, особенно для сеток с количеством узлов на луч больше 2000;

• 3)    в начале реакции происходит распад разрыва с образованием ударной волны и волны разрежения.

• 2.    Анализ результатов численного моделирования полной задачи показал, что после распада раз-

• рыва происходит зарождение и протекание само-поддерживающейся ТЯ реакции.