Математическое моделирование высокоскоростных процессов обработки давлением композиционных материалов на основе графита

Описание процесса высокоэнергетического прессования графитопластовой композиции [1, 2] требует знания деформирующего усилия, которое определяется взаимодействием фрагментов этой композиции. В настоящей работе рассматривается изменение удельных усилий, действующих на поверхностях контакта между твердой и мягкой со- ставляющими композиции в процессе прессования.

Процесс прессования условно разделен на две стадии. На первой стадии происходит сближение твердых компонентов композиции путем внедрения твердых составляющих в мягкую компоненту и заполнения пространства между ними. На второй стадии твердые

Порошковая металлургия и композиционные материалы компоненты входят в контакт между собой, упруго деформируются с формированием контактных площадок. Уплотнение структуры композиции реализуется за счет заполнения пространства, примыкающего к контактным площадкам.

Допускаем, что на контакте между фрагментами графитопластовой композиции распределение контактных давлений между фрагментами графитопластовой композиции соответствует эпюре, приведенной на рис. 1.

Определение величины внешнего усилия Р _е, действующего по всей контактной поверхности единичного фрагмента композиции, сводится к интегрированию функции распределения контактного давления Р к по поверхности контакта площадью А , т. е.

P e = JJ Р к dA . (1)

A

Следует отметить, что уравнение (1) остается в силе и в том случае, если внешнее усилие передается через недеформируемые компоненты композиции.

Решение интеграла (1) не вызывает затруднений, если известна функция P _к от координат точек, расположенных на площади проекции А , или если выразить эти координаты через координаты, в которых записана функция напряжений P _к .

В тех случаях, когда Pк является функцией только одной координаты, возможна замена двойного интеграла одинарным. Упроще- ния решений также достигается путем аппроксимации реальной формы контактирующих поверхностей упрощенными геометрическими формами: шаровой, цилиндрической, гиперболической, гиперболоидом вращения, параболической, эллиптической и др.

Рассмотрим решение интеграла (1) применительно к аппроксимированной форме твердого фрагмента композиции в виде шара.

Распределение нормальных давлений на поверхности шаровидного контакта при отсутствии трения примем в соответствии с формулой А.Д. Томленова [3]:

( n A

^Р к =° 5 I¹ + 2 - ^a l, ⁽²⁾

где a - угол между нормалью к контактной поверхности в рассматриваемой точке и направлением приложения внешнего усилия;

о 5 - предел текучести мягкой составляющей композиции.

Учитывая, что контактное давление описывается функцией только от угла α, и выражая угол α через радиус шаровой поверхности R и расстояние от точки, в которой рассматривается контактное давление до оси шаровой контактной поверхности ρ, измеряемое в плоскости, перпендикулярной к направлению приложения внешнего усилия (рис. 2), запишем интеграл (1) в виде

P e = JJ o 5 f 1 + П - arcsin R A P d P d Y . (3) A

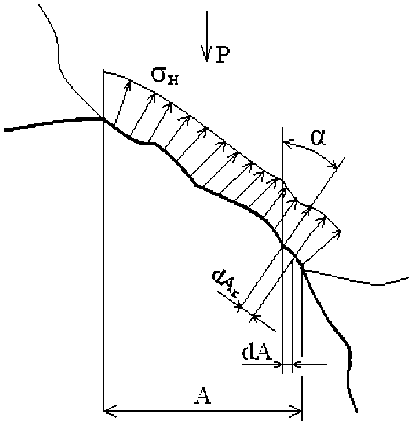
Рис. 1. Эпюра контактных давлений на поверхности твердой составляющей графитопластовой композиции

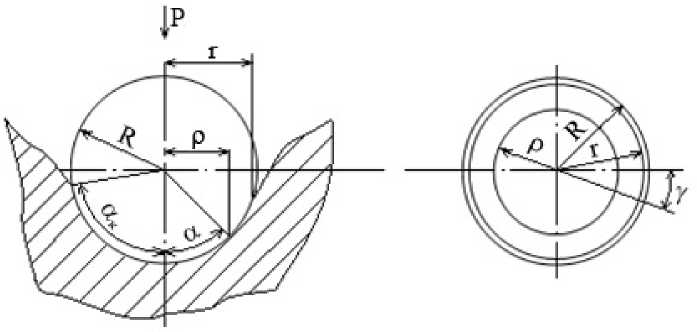
Рис. 2. Схема формирования контактной поверхности при внедрении твердой в мягкую составляющую композиции

Вычисляя интеграл (3) в пределах от γ = 0 до γ = 2π и по радиусу от ρ = 0 до ρ = r (см. рис. 2), запишем окончательно

Pe = ПГ2as X

жду твердыми составляющими, воспользуемся зависимостью И. Бочарова [4]:

X

1+-

—

I

I

—

R 2 1

2 r ² ,

r arcsin

R

—

R

2 r

I

^{1 —}

I

2 V^/2 1

R 2 1

. (4)

4a4 P = ""PS	3 a In	1	bS + — + c
Vsn		1 — yt I AI	h
			J

где

Максимальное усилие, развиваемое шаровидной твердой компонентой при внедрении в мягкую компоненту на величину половины своего размера, т. е. на величину осевого радиуса ( r = R ) будет равно

Pe = nR 2aJ1 + -|. (5) e S I 4 I

Относя усилие Р _е к площади проекции контакта на плотность, перпендикулярную направлению приложения внешней нагрузки, определяем удельное усилие прессования:

P y = a S 11 + 4 I» 1,785a S . (6)

Описанный метод оценки давления при прессовании учитывает только сопротивление внедрения твердых компонентов в мягкие, но не учитывает сопротивления заполнению мягкой составляющей пространства между твердыми составляющими.

Используя условие несжимаемости компонентов среды, задачу по заполнению мягкой составляющей пространства между твердыми решаем методом суперпозиции двух плоских процессов, протекающих во взаимноперпендикулярных плоскостях.

Для определения давления затекания мягкой составляющей в сужающиеся зазоры ме-

n 1    . S S Y a = — arcsin +

4 2        1 1 1

i n ,     ■ ( s Y

b = — + arcsin +

2 I 1 I

c = П

—

1—

S l

_ /                   -I        /     2

-1 S 1 + 11 S I A 1 — I S I 3111 311 JJ\   111

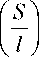
2 1 S

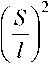
S – максимальный размер единичного очага деформации (по оси х );

l – расстояние между центрами смежных очагов деформаций по оси х ;

h – протяженность очага деформации по

оси y .

В процессе прессования возможно возникновение двух схем плотной упаковки: с расположением центров твердых составляющих в трех взаимноперпендикулярных плоскостях и со смещением их центров на величину радиуса их размера (рис. 3).

Для первой схемы имеем: S = R ; l = 2 R ; Δ = R ; h = 2 R . Подстановкой этих значений в уравнения (7) получаем: а = 0,8066; b = 2,094 и с = 1,228.

Вторая схема характеризуется следующими параметрами S , l , Δ и h : S = R /2; l = R ; h = 1,73 R ; Δ = 0,866 R . Таким параметрам соответствуют: а = 0,8066; b = 2,094; с = 1,228.

Порошковая металлургия и композиционные материалы

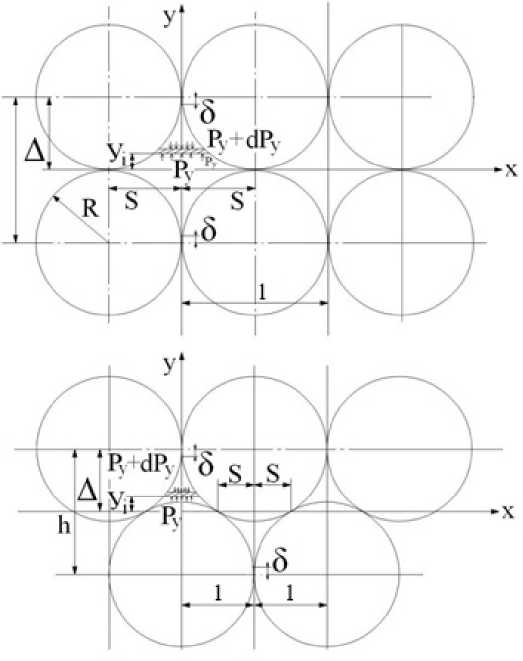
Рис. 3. Схемы плотной упаковки твердых составляющих композиции

Давления, необходимые для заполнения мягкой составляющей пространства между

твердыми компонентами композиции соответственно для первой и второй схем компо-

новки твердых составляющих, равны:

\

где R – радиус контактирующих сферических тел;

Е – модуль упругости материала контактирующих тел;

P_i – нагрузка, сжимающая сферические

P i =

^{4 о} ₅

3 п

4Ое

P ² = "7^

3 п

2,42ln

V

Г

2,42ln

—

yi

А

+ 2,27

;

V

—

y i

А 7

+ 1,83

.

тела.

При прессовании композиции максимально возможную сжимающую нагрузку выразим через твердость и размер контактной площадки:

P = HB -п5², (10) где НВ – твердость материала твердой компоненты.

Поскольку в процессе прессования все твердые компоненты входят в контакт между собой, то под действием сжимающего усилия смоделированные сферической формой твердые компоненты формируют площадки контакта в форме круга радиусом δ, который в соответствии с контактной задачей Герца для одинаковых размеров твердых частиц композиции определяется формулой [5]

5 = 0,88 3l ^p R , (9)

Подстановкой значения P_i в уравнение

(9) и преобразованием его относительно параметра δ получаем

, 0,681nHB R

5 =----------

E

.

С учетом контактной деформации твер-

дых составляющих максимальное значение

параметра у i в формулах (8) составляет

Г 0,681nHB 1_П

У = 1 —            R .

V e 7

Давление по первой и второй схемам

плотной упаковки твердых компонентов с учетом (12) равно:

4oc _

Р 1 =       ^2,42ln

V 3 n

0467 E 1 + 2,27

HB J

;

4ос

Р 2 =

V 3 п

( 0,404 E> 2,42ln ------ + 1,83 . , I HB J ,

Поскольку в реальных условиях прессования графитопластовой композиции расположение твердых составляющих возможно по разным схемам и с формой отличной от сферической, то расчет рекомендуется выполнять по усредненным значениям давлений и с учетом поправочных коэффициентов:

Р = ^1,47 ст s

2,42ln

0, 435 E HB

+ 2,05

x

X K Ф - K Т - K Ш , (14) где K _Ф – коэффициент, учитывающий отличие реальной формы твердой составляющей от сферической;

K _Т – коэффициент, учитывающий влия-

ние изменения температуры в процессе прессования на величину предела текучести мягкой составляющей композиции;

K _Ш – коэффициент, учитывающий заполнение мягкой составляющей шероховатого слоя твердой компоненты [6, 7].

Энергия формовочной машины затрачивается на диссипацию энергии в очаге деформации композиции:

L

Э = J p • F • dL , (15) 0

где p – давление, необходимое для заполнения мягкой составляющей пространства между твердыми компонентами;

F – площадь прессования композиции в плоскости, перпендикулярной приложению внешней нагрузки;

L – путь, проходимый бойком, от начала до конца прессования.

Если допустить прямопропорциональную зависимость между усилием прессования и перемещением пуансона, то диссипация энергии определится среднеинтегральным значением:

Э = 2>

V3n

2,42ln [ 0,435 E

I HB

+ 2,05 x

x L 0 - F - K ф - K _T - K ш.                 (16)

Выводы

Смоделирован процесс прессования графитопластовой композиции с использованием методов теории пластичности. Для решения объемной задачи применен метод суперпозиции процессов в двух взаимноперпендикулярных плоскостях. Процесс прессования графитопластовой композиции условно разделен на два этапа. На первом этапе реализуется процесс внедрения твердых компонентов в мягкую и заполнение пространства между твердыми компонентами мягкой. На втором этапе формируются площадки контакта между твердыми составляющими с заполнением пространства между ними мягкой составляющей. Получены математические зависимости для определения давления, реализуемого при внедрении твердой составляющей в мягкую и при заполнении пространства между твердыми составляющими мягкой. Дана оценка энергоемкости высокоэнергетического процесса прессования графитопластовой композиции.

Статья выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.A03.21.0011.