Математическое моделирование взаимосвязанных электромеханических систем непрерывной подгруппы клетей прокатного стана. Часть 1. Разработка математической модели

При прокатке полос в универсальных клетях толстолистового стана и черновой группы широкополосного стана горячей прокатки возникают ударные динамические нагрузки в электромеханических системах валков вертикальных клетей при захвате полосы валками последовательно расположенных горизонтальных клетей [1, 2]. Это связано с несогласованностью скорости выхода полосы из предыдущей вертикальной клети и линейной скорости валков горизонтальной клети. Причиной несогласованности являются недостаточная точность вычисления и задания скоростных режимов. Кроме того, в двухконтурной системе регулирования скорости электроприводов клетей при изменении нагрузки возникают статическая и динамическая ошибки регулирования скорости, которые не контролируются и не регулируются [3, 4]. Мгновенный подпор, формирующийся в полосе во время ее захвата валками последующей клети, воспринимается валками предыдущей клети в виде дополнительного сопротивления. В результате

Электромеханические системы в линии привода предыдущей клети возникает повторный колебательный процесс, а максимальный момент сил упругости становится соизмеримым с пиковым моментом при собственно захвате полосы [5, 6].

Экспериментальные исследования динамических нагрузок универсальных клетей показали, что при захвате полосы горизонтальными валками максимальный момент в вертикальных валках может превышать установившийся момент прокатки в 2–2,5 раза. В [7] представлены характерные осциллограммы, полученные на стане 2000 ОАО «Магнитогорский металлургический комбинат» (ОАО «ММК»), подтверждающие данный вывод.

Постановка задачи

Для исследования названного динамического режима необходима математическая модель, учитывающая передачу кинетической энергии на вал электродвигателя предыдущей клети через очаг деформации. Для этого необходимо наиболее точное описание очага деформации, основанное на балансе затрачиваемых мощностей и законе сохранения энергии. При этом математическая модель, описывающая упругие свойства полосы, может быть принята упрощенной, основанной на законе Гука, согласно выражениям, предложенным Н.Н. Дружининым и Д.П. Морозовым [8]. Это обосновано тем, что в черновой группе клетей отсутствует автоматическое регулирование толщины посредством изменения межвалкового зазора, принцип которого рассмотрен в [9, 10]. Более точная математическая модель полосы в межклетевом промежутке исследована в [11, 12].

Математическое описание автоматизированных электроприводов клетей может быть разрабо- тано без учета действия систем автоматического регулирования нулевого натяжения (САРНН) и автоматической коррекции скоростей электроприводов клетей. Это связано с тем, что динамические процессы при отработке мгновенного подпора определяются только настройкой быстродействующей двухконтурной системы автоматического регулирования скорости, в то время как САРНН вступает в работу только после захвата полосы валками последующей горизонтальной клети непрерывной подгруппы.

Основная часть

Структура модели взаимосвязанных электромеханических систем непрерывной подгруппы черновой группы стана 2000

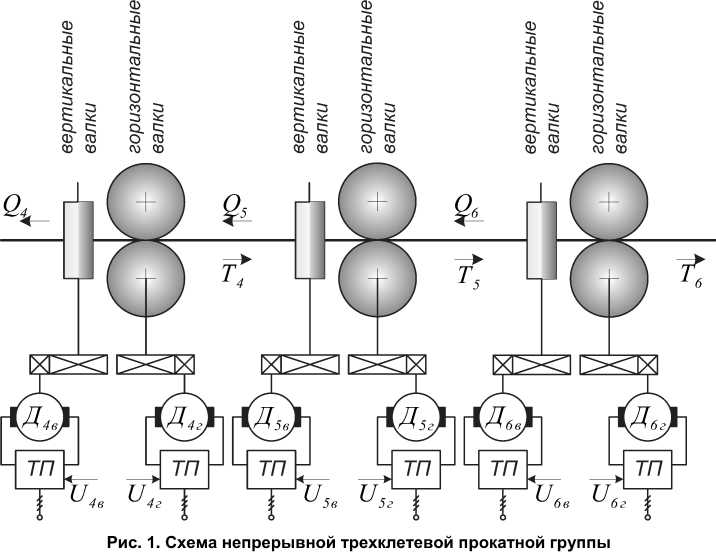
На рис. 1 показана непрерывная подгруппа черновой группы клетей № 4–6 стана 2000 ОАО «ММК». Универсальные клети содержат приводные вертикальные валки (двигатели Д 4в –Д 6в ) и горизонтальные валки, приводимые двигателями Д_4г–Д_6г, взаимосвязанные в процессе прокатки через обрабатываемую полосу [13, 14].

Анализ физических процессов, происходящих в трехклетевой группе как взаимосвязанной электромеханической системе, позволяет с целью создания математического описания разбить его на следующие объекты: автоматизированные электроприводы, клети (включая редукторы), очаги деформации, межклетевые промежутки. Причем если первые представляют собой различные технологические узлы и физические границы между ними легко определимы, то границы между очагами деформации и межклетевыми промежутками устанавливаются на поверхностях, все точки которых имеют скорости, равные скорости входа (выхода) металла в клеть [15, 16].

V_п в₄х S_п в₄х Q 4

вых вых

V п 6    S п 6    T 6

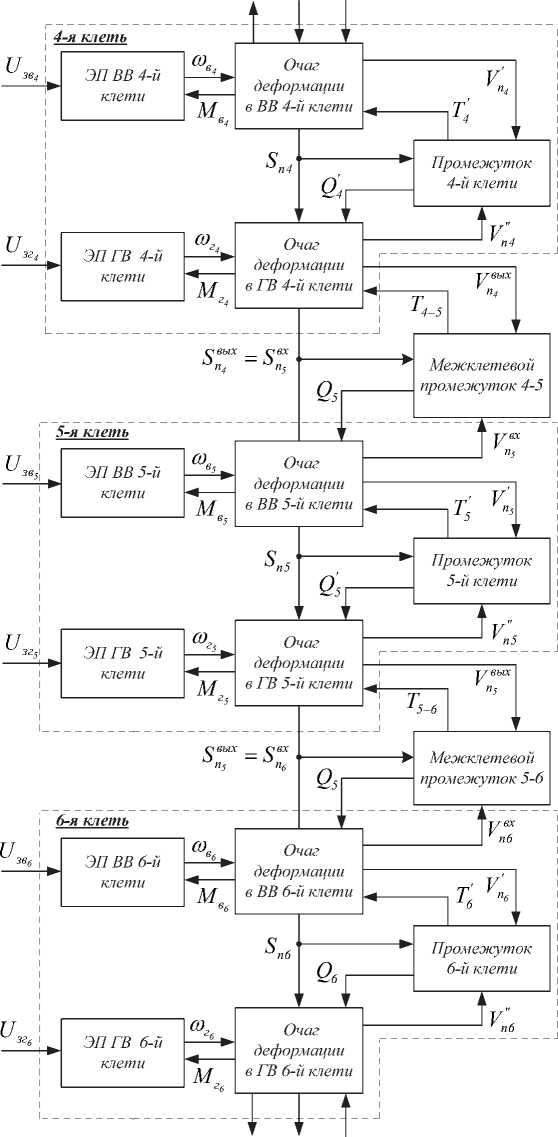
Рис. 2. Структурная схема математической модели взаимосвязанных электроприводов клетей № 4–6 стана 2000

Структурная схема комплексной математической модели взаимосвязанных электромеханических систем трехклетевой группы представлена на рис. 2. Структура содержит модели электроприводов (ЭП) вертикальных (ВВ) и горизонтальных валков (ГВ) клетей № 4, 5, 6 и модели поло- сы как объекта управления. Расшифровка обозначений, принятых на рис. 2, приводится ниже при описании математических моделей данных объектов.

Модель полосы представлена блоками «Очаг деформации в валках i -й клети», содержащими

Электромеханические системы математическое описание изменения давления и момента прокатки. В нее также входят блоки «Межклетевой промежуток ( i – 1) – i » и «Промежуток i -й клети», включающие математическое описание упругих свойств полосы между горизонтальными валками смежных клетей и вертикальными и горизонтальными валками универсальной клети. Как будет показано ниже, свойства полосы в этих промежутках описываются одинаковыми аналитическими зависимостями.

Модель имеет входные воздействия в виде напряжений управления на входах тиристорных электроприводов и шесть выходных координат: скорости полосы на выходе из вертикальных и горизонтальных валков, натяжения либо подпор в межклетевых промежутках и два возмущающих воздействия: заднее натяжение в первом очаге и переднее натяжение в последнем очаге деформации непрерывной подгруппы. В структуре модели содержатся логически связанные объекты, которые должны иметь входные и выходные координаты, согласующиеся между собой в количественных соотношениях. Далее рассматриваются математические описания отдельно каждого из этих объектов.

Математическое описание очага деформации

Математическая модель очага деформации разработана на основе закона сохранения энергии, упрощенная формула которого для процесса прокатки предложена В.Н. Выдриным [17]:

NB ± No ± N = N + N , (1) вiQiTiфiтi где Nв – мощность, подводимая к очагу деформации со стороны электропривода валков; NQ – мощность, подводимая к очагу деформации подпором Q (знак «–») либо натяжением (знак «+») через задний конец проката; NT – мощность, подводимая к очагу деформации тянущим усилием T (знак «+») либо подпором (знак «–») через передний конец проката; Nф – мощность, затрачиваемая на формоизменение (вытяжку) металла; Nт – мощность сил трения скольжения на контактной поверхности полосы с валками; i – порядковый номер клети.

В данном выражении не приняты во внимание мощность, расходуемая на упругую деформацию проката, мощность, затрачиваемая на создание дополнительных деформаций (сдвигов), обусловленных формой очага деформации, и другие виды мощностей (на изменение кинетической энергии проката и др.), удельный вес которых в балансе мощностей не превышает 2–3 % [18, 19].

Мощности, подводимые за счет переднего натяжения (подпора) и заднего подпора (натяжения), определяются согласно зависимостям [17, 18]

вых

N t = Т - V ™ ; N q = Q - V™ = Q - V— , (2)

вх вых где Vп , Vп – скорости проката на входе и выходе очага деформации; ц - вытяжка при прокат- ке, определяемая выражением:

ц =

вх

Sп вых Sп

вых

Lп вх , Lп вх вых вх вых где Sп , Sп , Lп , Lп – соответственно сечения и длины обрабатываемой полосы на входе в очаг деформации и на выходе из него.

Мощность, подводимая к очагу деформации от приводного двигателя, определяется как произведение элементарных сил трения т , направление которых совпадает с траекторией перемещения точек контактной поверхности, на окружную скорость валков V в , просуммированное по поверхности S соприкосновения металла с валками:

N в = // т ( S ) - К в ( S ) - dS . (3)

S

С учетом предположения о прямолинейном законе изменения ширины b и предела текучести металла вдоль очага деформации вх вых вх вых а + а . b +b а =----------, b =--------- и отсутствия упругой деформации валков

R = const, V = const

0<«<«а           в выражение (3) принимает вид:

N в = V в ' R в ' b ' / т- d а ,

а

где R _в - радиус валков клети; а - текущее значение угла в очаге деформации (в пределах от 0 до а ₀, см. рис. 3).

Направление продольной силы трения т в очаге деформации изменяется. Согласно теории жестких концов, предложенной И.М. Павловым [20], скорости Vпвх частиц входного сечения, как и ско- вых рости Vп   частиц выходного сечения очага дефор мации, равны между собой (см. рис. 3). При этом выполняется условие вх вых пвп.

Очевидно, что в этом случае в очаге деформации имеют место две зоны, показанные на рис. 3 [18]. В первой – зоне отставания – скорость металла ниже окружной скорости валков, поэтому энергия в ней передается от валка к металлу. Во второй зоне – зоне опережения, наоборот, скорость металла выше окружной скорости валков, следовательно, энергия передается в обратном направлении (от металла к валкам). Существует некоторый центральный угол у , определяющий линию на поверхности валков, в которой скорости металла и валка равны. Этот угол, как и указанную линию, принято называть критическим.

Данная схема построена для «классического» случая прокатки с передним натяжением и задним

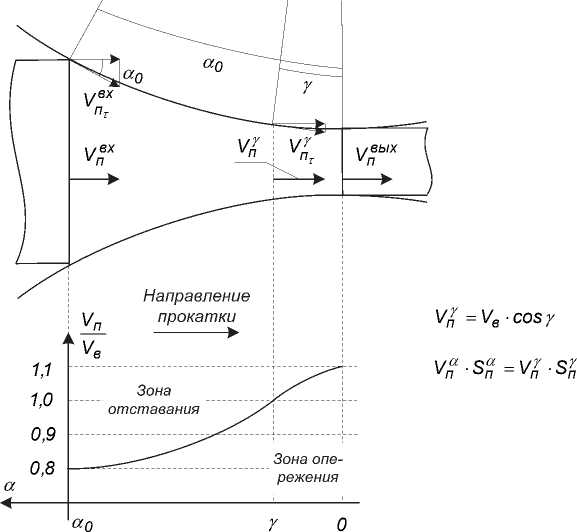
Рис. 3. Скольжение на поверхности полосы в очаге при равномерной деформации

подпором, возникающим вследствие отставания металла. Вместе с тем, представленные ниже выкладки справедливы для случая обратного распределения сил натяжения (подпора), возникающего при упомя- нутом выше повторном динамическом процессе. Отличия режимов натяжения и подпора должны быть учтены в конечной модели введением соответствующих знаков во взаимосвязях между блоками.

В зонах отставания и опережения продольные силы трения т' и т” направлены противоположно, поэтому выражение (6) для двух валков следует переписать в виде

N = 2■ V ■ R_ ■ b ■ [т I ■ d a- 2■[т II ■ d a . ввв

V о

При условии, что т = f a , f = const, Q(a(ao выражение (7) примет вид

N _B = 2■ f ■a V _B ■ R _B ■ b ■ ( a o -2■y ) ,

где a ₀ - угол захвата; a - сопротивление деформации; f – коэффициент трения.

Мощность формоизменения может быть получена путем дифференцирования зависимости Финка [17]:

Л ф = —ф = — ■ ( 9■a■ lnц ) = П' ^{d 9} см .    (10)

ф dt dt dt где Аф – работа, затрачиваемая на формоизменение проката; 9 - объем металла; 9см - смещенный объем при деформации.

В течение времени At через очаг деформации проходит объем металла, равный площади его критической поверхности S^ (поверхности внутри очага деформации, все точки которой имеют скорость, равную окружной скорости валков), умноженной на поступательную скорость частиц этой поверхности, соответствующей поступательной скорости валков в точке критического сечения Vву:

A9 = S „' ■ V 7 ■A t = S „' ■ V ■ cos у A t . п в п в

Площадь при принятом прямолинейном законе изменения ширины (рис. 4) определяется зависимостью [18]:

s n = b h ^y =

LBX bвых - bвх bвх +---------- ao/У

x[ h ^вых + 2 ■ R ■ ( I - cos y ) J .                  (11)

Указанный объем, определяемый размерами ( S^B ; V_n^BX ■ A t ), входит в очаг деформации, подвергается там конечной деформации ln ц и выходит из него с новыми размерами ( S ,^вых ; V_n ^B“^x ■A t ). Таким образом, смещенный объем за время A t будет определен как

A9см = A9 ■ ln ц = Sn ■ Vb ■ cos у ■ In ц ■ At, или при условии, что At ^ 0, d 9см = S^ VB ■ cos у* In Ц" dt.               (12)

После подстановки (12) в (10) получено выражение для определения мощности формоизменения при прокатке:

N ф =a^ S ^ Y ■ V_B ■ cosy^Inц .                  (13)

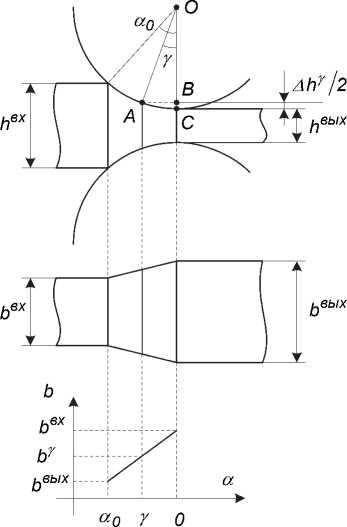
b^y = b^ex

OB cos у = -R- ^ ОВ = Re • cos у

— = BC = R_e 2^в

- OB =

= R_e - R e • cos У = R_e ' ( 1 - cos У )

h^y = h^eых + 2 • Ah^y =

= h^eых + 2 • R_e • ( I - cosy )

Ь вых - b вх «о/у

Рис. 4. К определению площади критической поверхности

Мощность трения скольжения на контактной поверхности N m также следует определять с учетом зон отставания и опережения. В общем случае для двух валков величина трения скольжения может быть найдена по выражению:

N т = 2 • JJ t ( S ) *A V ( S ) • dS ,

S или с учетом (4), (5), (8)

N _m = 2 • f •□• R в • b • J a V • d a .              (14)

a

Скорость скольжения металла относительно валков определяется зависимостями:

– для зоны отставания

A V ( a ) = V - V a =f 1 - S" 'cos ^Y )• V ; (15) ^B "            r*a              ^B

V S" • cos a J

– для полной мощности трения

N m = N T - N T = 2 • f •»• V b • R b • b X

‘? Г ^X Ф L Y ^V

^^^^^^»

i(

J 1 o V

^^^^^^B

– для зоны опережения

A V (a) = Va

S " • cos Y _V S ^a • cos a

-

1 | - V b ,

где S " , V„ - площадь поверхности соприкосно-

вения и поступательная скорость валков в точке, соответствующей текущему значению угла a .

При подстановке (15) и (16) в (14) получаем выражения мощностей трения скольжения:

– для зоны отставания

I

"0 f

= 2 • f •^ Vb • R в • b - J 1

Y V

^^^^^^в

S " • cos Y S a •cos a_v

– для зоны опережения

N T = 2 • f •g^

Vb • Rb • b •J

Г

1 -

S «• cos y) j d a ;

Sa • cos a J

S Lios! 1^ a S a • cos a J

S " • cos Y

S a •cos a

• d a

При условии постоянства угловой скорости валков на протяжении всего очага деформации N с учетом соотношения момента и мощности M = га выражения (1), (2), (13), (17) для i -й клети можно представить в виде:

M в _i

M _Тi

MQ - MT + MФ,- + Mmi , вых z‘ ni

® B ,     ’

^MQ =

Q i " VB^X ® B , ’

^M Ф , =^g i • S " • R B i • ^cos Y i • ln ^- ,

M_m = 2 • f •a_r R ² • b x т_iii в _ii

^a o i

X

J 1

^^^^^^B

S ^Y • cos y,- " i             ^Y i

Y i

S a • cos a i

^Y i f S " • cos Y i

+j

a

S_n . • cos a i

^^^^^^B

• d a i +

)

1 • d a i

где площадь в произвольном сечении (в том числе нейтральном) может быть найдена из (11) при пренебрежении уширением:

s n a i = g^ + 2 . R B i. b₄ . ( i - cos a ) ,          (23)

S^ s + 2 ■ R Bi. b _r(1 - cos yj,         (24)

где S_п^в _i ^х , S_п^в _i ^ых – площади поперечного сечения

Математическая модель полосы

полосы на входе и выходе i - го очага деформации .

Угол нейтрального сечения может быть опре делен по зависимости (9):

^ao i.           М . i

^^^^^^^^^^^^^^^^^^^B  ^^^^^^B  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

в межклетевом промежутке

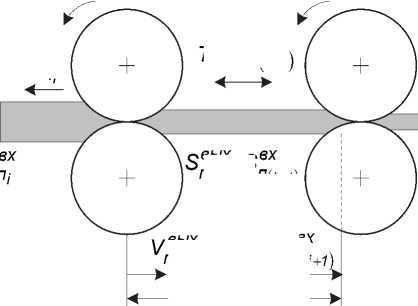
Изменение свойств полосы на участках между очагами деформации поясняется с помощью рис . 6. Вследствие несоответствия мгновенных значений скоростей выхода полосы из предыдущей клети и входа в последующую клеть возникает натяжение ( подпор ). Под действием этой силы полоса упруго деформируется : при натяжении – удлиняется и утончается , при подпоре – укорачивается и уширя ется . При этом упругая деформация может быть описана интегральными уравнениями [8]:

Скорость металла на выходе из клети опреде ляется угловой скоростью вращения валков и за висит от величины критического угла

2 - « - R .? - b

V . -« .V R . i +      ._ ..-' - cos Y i ) . (26)

п

Q i =

Скорость металла на входе в клеть :

вх п

вых

V п

H i

Изменения сечения обрабатываемого металла и его сопротивления деформации могут быть оп -

вых

E'Sn Ti= -Л-

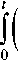
V вх

. ( i +1)

e - s”

L Q i

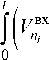
ых

V . ( i - i ) ) dt Q

вых пi              начi

где Е_i – модуль упругости ; L_{T i} , L_{Q i} – длины уча - стко полосы , на которых дейст уют силы T_i и Q_i ; Т , Q – начальные переднее и заднее натяже - ⁱнач ⁱнач

ния .

Дифференцируя за исимости (31), (32) и пе реходя к операторным изображениям , получаем :

ределены как :

вых S_п

S п ^{в х}

,

H i

^ i ⁿ- 1 ^И- , „ _ ⁿ i - 1^{+ n} i

СФi      Э

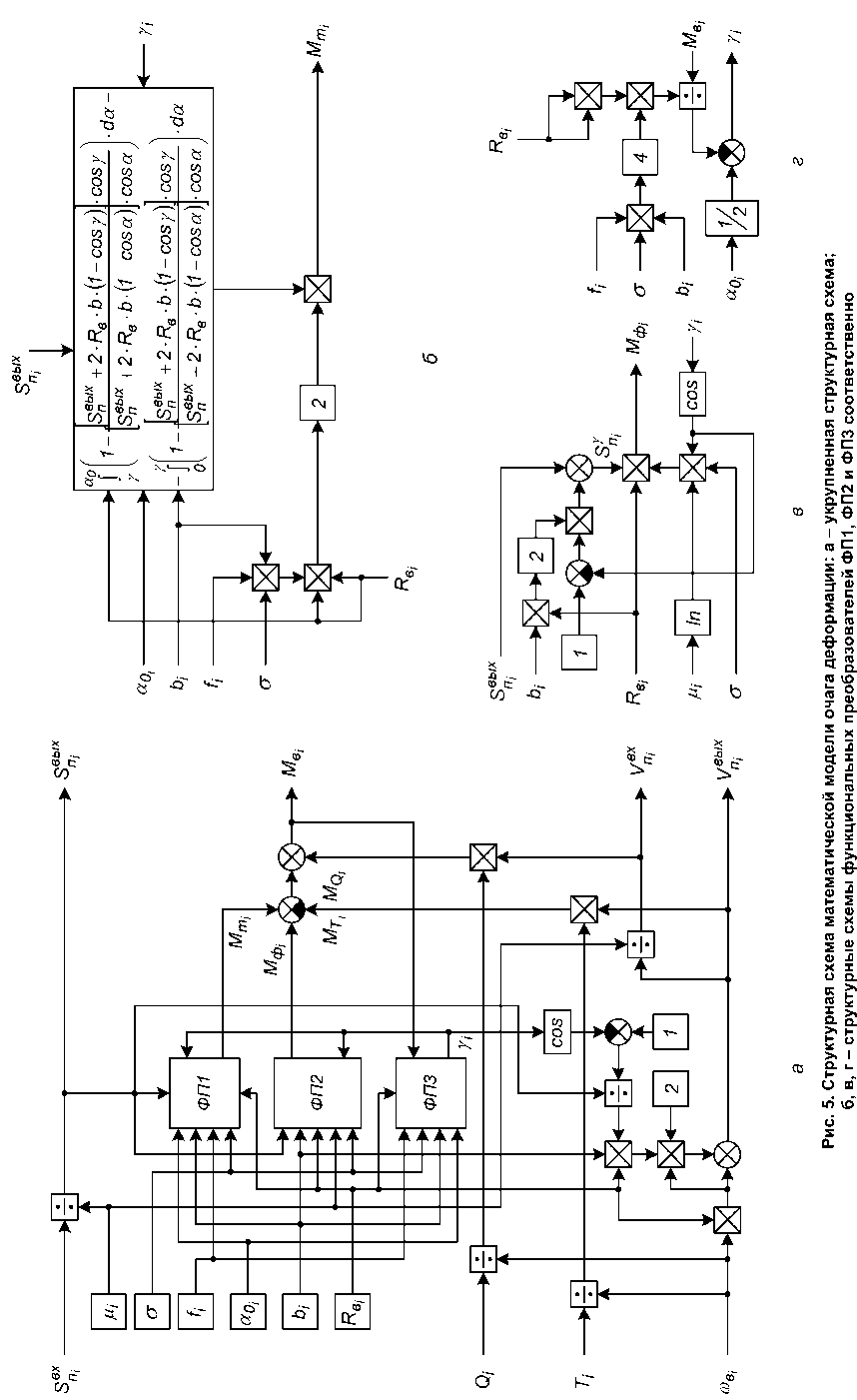
На рис. 5 приведена структурная схема математической модели очага деформации, составленная по уравнениям (18)–(30). Функциональные преобразователи ФП1…ФП3 реализуют зависимости (22), (21) и (25) соответственно. Представленная математическая модель наиболее точно определяет взаимосвязь между четырьмя входными и четырьмя выходными координатами, представленными на рис. 2.

ых

E -S p ^T* (p )=-1ТТ7 ■( V.-■   V.B ых) •       (33)

E SX p-Q( p ) =       ■( Vn.x - V^)) •         (34)

Qi где р = dd- - оператор дифференцирования по ремени.

Согласно этим ыражениям усло иях с ободной прокатки T_t = Q ( i ₊ i ) . При возникновении натяжения T = Q (_{t + 1} ) ) 0 , при подпоре T i = Q ( i _{+ 1} ) ( 0 .

Влияние ертикальных алко на процесс формиро ания межклете ого натяжения и подпора значимо, но не елико, поскольку мощность уста-

S

Q i

®ei юв (i+1)

S п (i+1)

L T i

V вх п (i вых пi вых пi

Рис. 6. Расчетная схема межклетевого промежутка

Т i = Q ( i+1 )

■ вых п (i+1)

новленных электродвигателей меньше мощности двигателей приводов горизонтальных валков более чем в 50 раз. Влияние на натяжение (подпор) несогласованности окружной скорости вертикальных валков может быть учтено выражением

М^ - М_хх - М

A T = A Q , i + i ) = -^Э----^Э----    ,     (35)

R вЭ где МвЭ – момент на бочке вертикального валка (эджера); МххЭ – момент холостого хода; М дефЭ – момент, необходимый для деформации металла в вертикальных валках; RвЭ – радиус вертикальных валков.

На рис. 7 приведена структурная схема динамической модели межклетевого промежутка, составленная по уравнениям (33)–(35). Она наглядно представляет взаимосвязь между тремя входными, одной выходной координатами и одним возмущающим воздействием.

S

A Ti вых пi

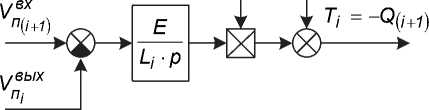
Рис. 7. Структурная схема математической модели межклетевого промежутка

Статический момент, создаваемый электродвигателем клети, может быть определен как сумма момента на бочке валков M _{в i} , идущего на деформацию металла, и момента, необходимого для преодоления сил трения механизма М _{хх i} , приведенного к валу двигателя. В этом случае при пренебрежении упругими свойствами поведение редуктора описывается системой операторных уравнений:

М, Рр}          1

М с( р ) = в     + М хх,( р)

j ред j

г, м р )=^

j ред, где jред – передаточное число редуктора (для понижающего редуктора jред, > 1); Мс, - момент сил статического сопротивления, приведенный к валу двигателя; ®дв , - угловая скорость двигателя i -го валка.

Математическая модель системы регулирования скорости электропривода

Модель каждого межклетевого промежутка включает модели электроприводов горизонтальных и вертикальных валков в замкнутых двухконтурных системах однозонного регулирования скорости. Поскольку структуры и настройки систем управления этих электроприводов идентичны, ниже приводится описание модели якорной цепи, общей для обеих групп электроприводов. Данная модель описывается известной системой операторных уравнений [21]:

E d, =

^к тп

Т „ Р + 1

u у ;

E d, = E дв , + R э , 1 я , ( Т э , р + 1 ) ;

‘ м , = кФ _ш 1 я , ;

Е дв , = ^кФ н , ® , -;

М, - Мс, = JXi Р®i, где Ed и Eдв – ЭДС тиристорного преобразователя (ТП) и двигателя; ктп и Т„ - коэффициент усиления и постоянная времени ТП; uy – напряжение управления ТП; Rэ и Тэ – эквивалентные активное сопротивление и постоянная времени якорной цепи; М и Мс – моменты двигателя и статических сопротивлений, приведенные к валу двигателя; Iя – ток якорной цепи; JΣ – суммарный приведенный момент инерции; Ф – поток возбуждения; к – конструктивная постоянная двигателя.

Структурная схема математической модели двухконтурной системы автоматического регулирования скорости электропривода, соответствующая системе уравнений (36), представлена на рис. 8. Синтез регуляторов тока и скорости для каждого электропривода выполнен по известной методике синтеза систем подчиненного регулирования [22].

Блок переключения (БП) введен в структуру электропривода для моделирования разработанного способа ограничения динамических нагрузок в электромеханических системах универсальной клети [7, 23]. С его помощью запоминается среднее значение тока свободной прокатки, при входе полосы в последующую клеть осуществляется размыкание контура регулирования скорости и запомненное значение тока подается на вход регулятора тока.

Преимуществом разработанной модели, является то, что она может быть применена для исследования динамических режимов в электромеханических системах универсальных клетей независимо от рода тока электропривода. Так, для исследования электроприводов переменного тока вместо модели, представленной на рис. 8, в структуру модели на рис. 2 (блоки «ЭП ВВ -й клети» и «ЭП ГВ -й клети» должны быть включены модели замкнутых двухконтурных систем регулирования скорости асинхронного либо синхронного двигателей, рассмотренные, например, в [24, 25].

Оценка адекватности математической модели

Адекватность разработанной математической модели исследуемому объекту оценивалась по результатам сравнения переходных процессов координат электроприводов и параметров прокатки, полученных при моделировании и путем ос-циллографирования на стане 2000.

При моделировании приняты параметры прокатки полосы из сляба шириной 1600 мм, марка стали 08Ю, экспериментальное исследование прокатки которого проводилось на стане. Толщина полосы на входе в клеть № 4 - 120 мм, обжатия в клети № 4 - 40 мм (33 %), в клети № 5 - 30 мм (38 %), в клети № 6 -20 мм (40 %). Скорости полосы при свободной прокатке на выходах клетей № 4, 5 и 6: 1,05; 1,91 и 3,66 м/с соответственно [3, 26].

Характерные осциллограммы переходных процессов, полученные экспериментальным способом для электроприводов горизонтальных валков клети № 4, представлены на рис. 9, а. На рис. 9, б показаны аналогичные переходные процессы, полученные расчетным путем с использованием разработанной математической модели. На осциллограммах и расчетных кривых указаны фиксированные параметры, по которым проводилось сравнение данных в характерных точках. Для других координат электромеханических систем межклетевого промежутка адекватность оценивалась аналогично.

Результаты сравнения экспериментальных и расчетных данных, представленных на рис. 9, позволяют сделать вывод, что в большинстве характерных точек относительная погрешность

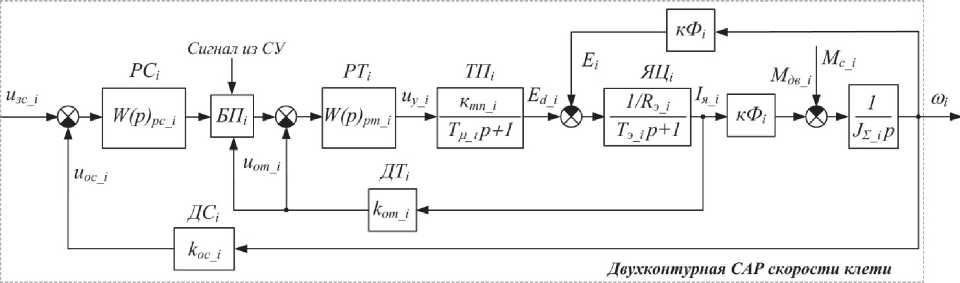
Рис. 8. Структура математической модели электропривода i -й клети как объекта управления: ЯЦ - якорная цепь; РТ - регулятор тока с передаточной функцией W(p)_pm ; РС - регулятор скорости с передаточной функцией W(p)_pm ; ДТ - датчик тока; ДС - датчик скорости; БП - блок переключения; к_от, к_ос - коэффициенты датчиков; и _от, и _ос -напряжения обратных связей по току и скорости

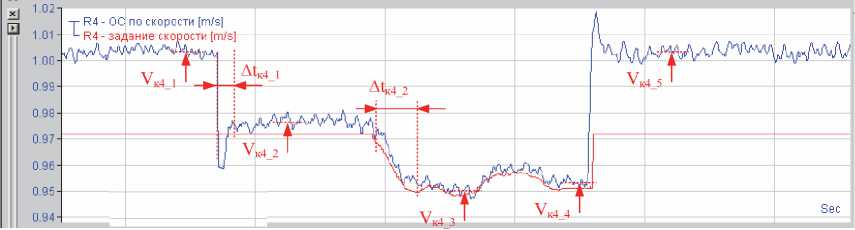
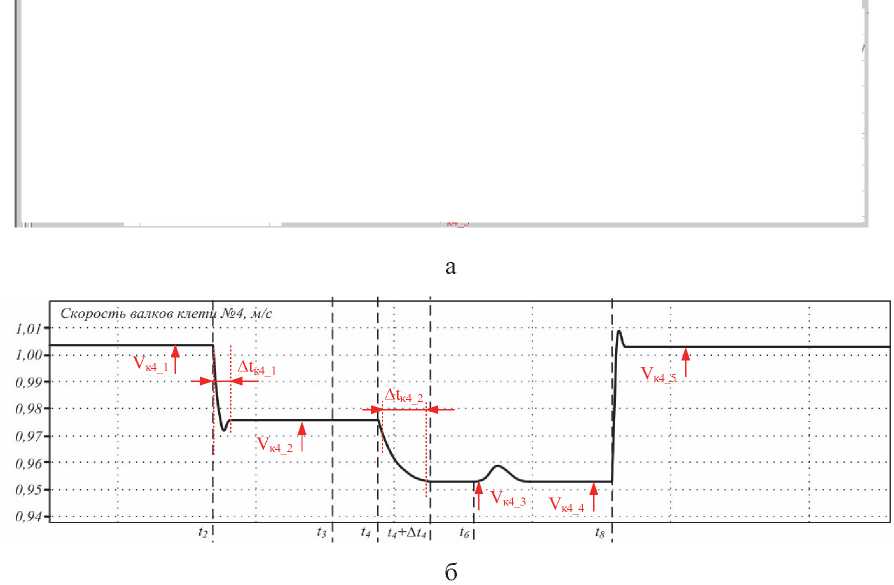
Рис. 9. Оценка адекватности математической модели по скорости горизонтальных валков клети № 4

не превышает 5 %. Такие расхождения находятся в пределах погрешности измерений и являются допустимыми при моделировании сложного взаимосвязанного объекта. Аналогичный анализ адекватности математической модели выполнен по скорости вертикальных валков клети № 4, результаты представлены в [27].

Заключение

Ударное изменение нагрузки, возникающее в электромеханической системе вертикальных валков при захвате полосы горизонтальными валками универсальной клети, представляет собой сложный динамический процесс, исследование которого целесообразно выполнить методами математического моделирования. Разработанная математическая модель взаимосвязанных электромеханических систем трехклетевой непрерывной группы прокатного стана позволяет наиболее точно исследовать процесс передачи кинетической энергии через очаг деформации.

Достоверное математическое описание силовой взаимосвязи электроприводов смежных горизонтальных и вертикальных клетей позволяет анализировать причины отклонений натяжения либо возникновения подпора в межклетевых промежутках. Это обеспечит возможность исследования усовершенствованных алгоритмов регулирования нулевого натяжения [28, 29].

Модель рекомендуется для анализа динамических режимов, возникающих в электроприводах универсальных клетей при управляющих и возмущающих воздействиях. Применение модели также целесообразно при исследовании разработанного способа снижения динамических нагрузок в черновой группе клетей широкополосного стана горячей прокатки [1, 23].

Работа выполняется в рамках госзадания (№ 2014/80) Министерства образования и науки РФ.