Математическое обеспечение метода планирования подготовки систем контрольно-проверочной аппаратуры к испытаниям электро- и радиосистем космических аппаратов на техническом комплексе

Задача планирования подготовки систем контрольнопроверочной аппаратуры (КПА) к проведению электрических испытаний (ЭИ) космических аппаратов (КА) на техническом комплексе (ТК) заключается в последовательном решении таких задач, как оценивание значений показателей работоспособности систем КПА на текущий момент времени и прогнозирование их изменения на период проведения ЭИ КА; определение на основе полученного прогноза необходимости проведения предупредительных мероприятий, их объема, а также объема операций контроля технического состояния систем КПА; составление оптимального плана подготовки этих систем к проведению испытаний, обеспечивающего завершение процесса их подготовки к моменту начала ЭИ КА.

Для решения перечисленных задач необходимо построение комплекса математических моделей, включающего математическую модель для расчета значений показателей надежности систем КПА, математическую модель процесса их подготовки к проведению испытаний, а также прогнозную модель технического состояния систем КПА.

Для получения информации о характеристиках безотказности систем КПА в текущий момент времени авторами предложена модель для расчета значений показателей их надежности. Данная модель учитывает структуру систем, выполняемые ими функции, позволяет использовать имеющуюся статистическую информацию за предшествующий период эксплуатации и, в конечном счете, делать заключение о работоспособности систем КПА в текущий момент времени. Необходимость построения математических моделей систем КПА связана с тем, что структурная сложность и малосерийность систем КПА ЭИ КА, а также поддержание их постоянной готовности к проведению испытаний делают невозможным осуществление экспериментальных исследований надежности КПА.

Из всей совокупности рассмотренных моделей в рамках сформулированной задачи системы КПА наиболее адекватно описывают модели в виде аналитических выражений, с помощью которых можно отразить структурные и функциональные особенности анализируемых систем, и которые позволяют использовать имеющиеся статистические данные. Именно эти модели и положены в основу разработанной модели для расчета значений показателей надежности систем КПА ЭИ КА.

Для определения вероятности безотказной работы систем КПА в течение ЭИ КА сформулирован критерий отказа систем КПА при проведении этих испытаний. Процесс проведения ЭИ может быть представлен как определенная их программой последовательность выдачи системами КПА в требуемые моменты времени управляющих воздействий (УВ) на борт КА и получение квитанций об исполнении этих воздействий. При этом считается, что отказом системы КПА при проведении ЭИ КА будет являться событие, заключающееся в нарушении работоспособности системы КПА при выдаче любого управляющего воздействия или при приеме любой квитанции с борта КА.

Обозначим через A_j событие, заключающееся в отказе системы КПА при выдаче (приеме) УВ (квитанции). Тогда

Р ( A j ) = 1 - Р ( t j ), (1) где P ( t_j ) – вероятность безотказной работы (ВБР) системы КПА в момент времени t_j выдачи j- го УВ.

Очевидно, что безотказность системы КПА при выдаче (приеме) УВ (квитанции) определяется безотказностью совокупности элементов системы, участвующих в выдаче (приеме) данного УВ (квитанции). Эта совокупность является частью структурно-функциональной схемы системы КПА, в соответствии с которой для каждого УВ (квитанции) можно составить схему прохождения УВ (квитанции). Эта схема может иметь разную степень детализации, в зависимости от того, что рассматривается в качестве элемента системы. Детализация схемы прохождения УВ (квитанции) в данной статье была осуществлена до невосстанавливаемого элемента системы КПА, которым может являться модуль или блок системы.

Схему прохождения УВ (квитанции) можно представить в виде структурной схемы надежности (ССН). Принимая в качестве допущения независимость отказов модулей системы и их нагруженное резервирование, вероятность P ( t_j ) безотказной работы системы в момент выдачи j- го УВ определим следующим образом:

z

Р (t j ) = П P z (t j ) (2) z = 1

где P_z ( t_j ) – ВБР участков последовательного соединения схемы прохождения j -го УВ (квитанции) в системе КПА; z – число участков последовательного соединения схемы прохождения j -го УВ (квитанции).

Обозначим через А событие, заключающееся в не-прохождении хотя бы одного УВ (квитанции) в течение ЭИ КА. Очевидно, что событие А задается событиями А . , заключающимися в непрохождении j -го УВ (квитанции), а вероятность Р ( А ) наступления события А - вероятностями Р ( А . ) наступления событий А . . Эту зависимость в общем виде можно представить как

Р (А ) = f (Р (А 1 ),... Р (A j ),... Р (А к )), (3) где k - число выдаваемых (принимаемых) УВ (квитанций).

События A .. ., А_к могут быть зависимыми или независимыми. Наличие зависимости между данными событиями определяется наличием общих участков в схемах прохождения УВ (квитанций). Для двух событий А, , А . при наличии общих участков в режимах выдачи (приема) i -го и j -го УВ (квитанции) вероятность Р(AA j ) того, что не пройдет и i -е, и j -е УВ (квитанция), имеет вид

Р ( А А . ) = Р ( А ) Р ( А . ) + r ( А А ), (4) где r ( A A . ) - коэффициент корреляции событий А . и А . .

Коэффициент корреляции r ( AA j ) характеризует степень зависимости этих событий:

P ⁽ A . ) - Р ⁽ A j )Р ⁽ A j )

r ^{( A}i ^Aj )    ,                —     — ,         ⁽⁵⁾

V Р ( A i )Р ( A j ) Р ( A i ) Р ( A j )

где P ( A j ) - вероятность наступления события A j , заключающегося в нарушении работоспособности общего участка в схемах прохождения i -го и j -го УВ (квитанции). Таким участком может быть как отдельный модуль, так и совокупность модулей. Тогда с учетом зависимости отказов вероятность безотказной системы КПА за время т э _и проведения ЭИ в общем виде можно представить как

Р (Тэ.и ) = 1 - Р (A) = 1 -- f [ Р ( Aj),..., Р ( al ),{ Р ( AiAj )}], где L - число УВ, отказы при выдаче которых не зависят от отказов при выдаче других УВ.

Таким образом, выражения (3)...(6) являются математической моделью надежности систем КПА, которая учитывает структуру этих систем, выполняемые ими функции, наличие общих участков в схемах прохождения УВ (квитанций) и предысторию эксплуатации системы КПА.

Эта модель стала основой разработанной авторами математической модели процесса подготовки системы КПА к проведению испытаний, с помощью которой можно определить зависимость длительности подготовки этой системы к проведению испытаний от случайных величин, в частности момент начала подготовки систем КПА к испытаниям, и планировать весь этот процесс.

Процесс подготовки системы КПА состоит из двух групп отдельных технологических операций: группы операций контроля и группы операций восстановления. Первая группа операций проводится последовательно, поэтому их совокупность можно рассматривать как одну макрооперацию контроля с вложенной (при необходимости) технологической операцией восстановления. Аналогично последовательность технологических операций восстановления можно рассматривать как одну макрооперацию восстановления, после которой повторяются в необходимом объеме технологические операции конт роля. Тогда процесс подготовки системы КПА к проведению испытаний можно рассматривать как последовательность трех макроопераций: контроля, восстановления и контроля после восстановления. В этом случае в качестве модели подготовки системы КПА к проведению испытаний можно использовать двухуровневую модель, в которой модели разных уровней имеют различную степень детализации протекающих при этом процессов: модели первого уровня детально описывают технологические операции контроля и восстановления, а модель второго уровня рассматривает процесс подготовки систем КПА к проведению испытаний в целом. С учетом этого для описания подготовки системы КПА к проведению ЭИ используем двухуровневую модель графа переходов системы КПА во множестве возможных состояний (рис. 1).

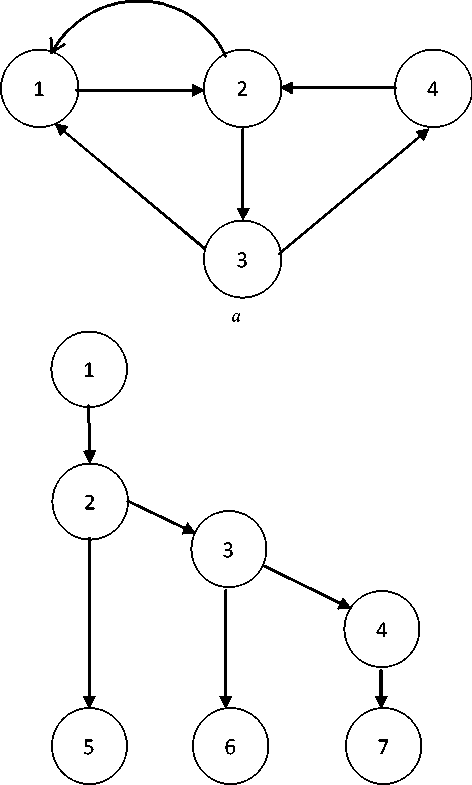
б

Рис. 1. Графовые модели системы КПА при проведении технологической операции контроля:

а - модель графа переходов; б - геометрическая модель структурного графа; 1 - система КПА готова к проведению очередной операции контроля; 2 - состояние, характеризуемое проведением операции контроля;

3 - состояние идентификации выявленного отказа;

4 - состояние выполнения операции восстановления;

5, 6, 7 - системой КПА завершено выполнение операции контроля и она готова к выполнению очередной операции

Модель технологической операции контроля. Эта модель представляет собой модель графа переходов системы КПА во множестве возможных состояний при проведении отдельной операции контроля (рис. 1, а ).

Следует отметить, что длительность операции контроля определяется рядом величин. К ним следует отнести временные затраты на выполнение операции контроля, идентификацию выявленного отказа и восстановление отказавших модулей в случае их отказов при проведении операции.

С учетом этого замечания перейдем от замкнутого графа к структурному графу (рис. 1, б).

Введем следующие обозначения:

• -    z ⁺ - момент завершения макрооперации контроля при подготовке системы КПА к проведению испытаний;

• -    z ⁺ ( к ) - момент завершения к -й контрольной операции (КО), к = 1, К , где К - число КО;

• -    z f ( к ) - момент перехода в состояние f при проведении к -й операции контроля;

• - S ( к ) - длительность операции восстановления при обнаружении отказа во время проведения к -й операции контроля.

С учетом этих обозначений плотность ф z ₊ ( и ) распределения вероятностей момента z ⁺ завершения макрооперации контроля определяется с помощью следующей системы рекуррентных выражений:

ф _z +⁽ и ) = ф _z + ( К )⁽ и ).

ф +   (и ) = Р1Ф z 5-( к)(U ) + z (к)

^{+ Р}2 [ ^Р 3^ф z 6 ' ( к )⁽ u ) ^{+ Р} 4^ф z 7 ' ( к )⁽ u ^)] , ^ф z 2'( к )⁽ u ) = ^ф z + ( к - 1)⁽ u ), ^ф z 5'( к )⁽ u ) = ^ф z 2'( к )⁽ u ⁺ t^k к.о X ^ф z 3'( к )⁽ u ) = ^ф z 2'( к )⁽ u ⁺ t^k к.о X ф z 4'( к )⁽ u ) = ф z 3'( к )⁽ u )ф t_u ^{( и} ), ф z 6'( к )^{( и} ) = ф z 3( к )^{( и} )9 t_u ^{( и} ), ^ф z7(к )^{( и} ) = ^ф z 4'( к )^{( и )ф} S ( _к ) ^{( и} X

Коэффициенты Р 1 , Р ₂ , Р ₃, Р ₄ имеют следующий смысл: R . _ ^f

Р = П p м (Т \ r=1

Р 2 = 1 — Р 1 ,

Р 1 + Р 2 = 1,

Р3 =1

1 при qsk е М ij 0 при qks е M ij

P4 = 1 — Р3, где Pr(Т) - вероятность безотказной работы отдельного проверяемого модуля, рассчитанная с помощью модели надежности системы КПА; Mj = {mij}= Mi n Mj -множество модулей, проверяемых в i-й и j-й КО, i ^ j, i = 1, ..., K, j = 1, ..., K; q^ - число отказавших модулей при проведении к-й КО.

Соотношения (7), (8) представляют собой математическую модель технологических операций контроля в системе КПА, образующих макрооперацию контроля при подготовке этой системы к проведению ЭИ.

Модель технологической операции восстановления. Эта модель (рис. 2) представляет собой модель графа переходов системы КПА при проведении технологической операции восстановления во множестве возможных состояний (рис. 2, а ).

Перейдем от замкнутого графа к структурному графу (рис. 2, б ).

Введем следующие обозначения: S ⁺ - момент завершения макрооперации восстановления; S ⁺ ( v ) - момент завершения v -й операции восстановления, v = 1, V , где V = S - L + D - число технологических операций восстановления, здесь S - число отказавших модулей, L - число модулей, восстановленных при проведении К О, D - число модулей с потенциальными отказами; t l - средняя длительность определения типа отказавшего модуля; S q ( v ) - момент перехода системы КПА в состояние q при проведении v -й операции восстановления.

С учетом введенных обозначений запишем систему, позволяющую построить плотность фs + (и) распределения вероятностей момента S + завершения макроопера- ции восстановления:

^ф s + ^{( и} ) = ^ф s + ( v )^{( и} ),                  '

^ф s + ( v )^{( и} ) = ^р 1^ф s 6- ( v )^{( и} ) ^{+ +} = Р 2 ^ф s 7- ( v )^{( и} ) ⁺ Р 3^ф s 8- ( v )^{( и} ), ^ф s 2-( v )^{( и} ) = ^ф s + ( v - 1)^{( и} ), v = 2^ ^ф s 3- ( v )^{( и} ) = ^ф s 2-( v )^{( и + ?} о ),        ,           ₍9

^ф s 4- ( v )^{( и} ) = ^ф s 2-( v )^{( и + Г} о ),                    '

^ф s 5-( v )^{( и} ) = ^ф s 2-( v )^{( и +} t o ), ^ф s б-( v )^{( и} ) = ^ф s 3-( v )^{( и} ) ■ ^ф 1 3^{( и} ), ^ф s 7-( v )^{( и} ) = ^ф s 4-( v )^{( и} ) ^ ^ф td ^{( и} ), ^ф s 8-( v )^{( и} ) = ^ф s 5-( v )^{( и} ) ^ ^ф t р ^{( и} ).

Коэффициенты Р ₁, Р ₂, Р ₃ имеют следующий смысл:

Р_х = Р ( q s е G ), P 2 = P ( q^k_s е G ), ^Р 1 ^{+ Р} 2 ^{+ Р} 3 = ¹ Р 3 = 1 - ( Р 1 + Р 2 ).

Соотношения (9), (10) представляют собой математическую модель технологических операций восстановления в системе КПА, которые составляют макрооперацию восстановления при подготовке этой системы к проведению ЭИ.

Модель подготовки системы КПА к проведению испытаний. Совокупность макроопераций контроля технического состояния системы КПА и восстановления работоспособности системы составляет процесс подготовки системы КПА к проведению ЭИ.

Для получения закона распределения длительности подготовки системы КПА к проведению испытаний воспользуемся графом переходов системы КПА во множестве возможных состояний (рис. 3).

В соответствии с моделью последовательных переходов запишем следующее выражение:

t = T + tK + tfi + tК ,                (11)

нквк где t – длительность проведения подготовки системы КПА к проведению испытаний; tк = z+ = z(K) - длительность проведения макрооперации контроля технического состояния; tв = S+ = S+ (V) - длительность проведения макрооперации восстановления работоспособнос-

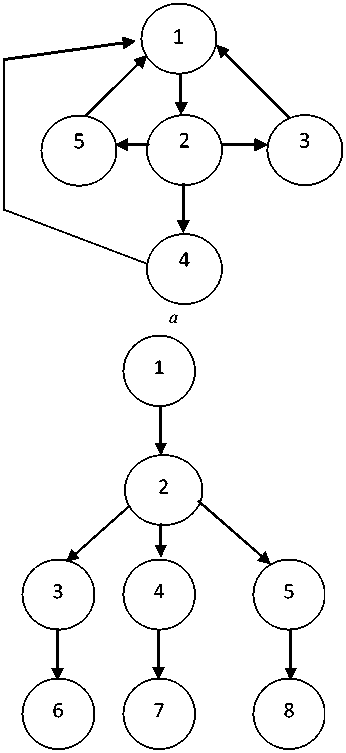
б

Рис. 2. Графовые модели технологической операции восстановления систем КПА: а – модель графа переходов системы КПА при проведении технологической операции восстановления; б – геометрическая модель структурного графа; 1 – система КПА готова к проведению очередной операции восстановления; 2 – состояние определения принадлежности отказавшего модуля множеству Z модулей, имеющихся в составе ЗИП системы КПА, и множеству G модулей, имеющихся в составе ЗИП аналогичной системы;

• 3    – состояние восстановления системы КПА, в случае если отказавший модуль принадлежит множеству Z (замена отказавшего модуля исправным из состава ЗИП системы);

• 4    – состояние восстановления системы КПА при принадлежности отказавшего модуля множеству G (замена отказавшего модуля исправным модулем из состава ЗИП аналогичной системы); 5 – состояние восстановления системы КПА путем ремонта отказавшего модуля; 6, 7, 8 – системой КПА закончено проведение операции восстановления и она готова к выполнению очередной операции восстановления

ти системы КПА; t К = z ⁺ = z ( М ) - длительность проведения макрооперации контроля технического состояния после окончания макрооперации восстановления работоспособности системы КПА; М – количество операций контроля, необходимых для проверки V восстановленных модулей; T _н – оптимизируемый параметр – момент начала подготовки системы КПА к проведению испытаний.

Выражение (11) позволяет установить зависимость между характеристиками временных затрат на подготовку системы КПА к проведению испытаний и оптимизируемым параметром – моментом начала подготовки системы.

Введем ряд обозначений: T ^К – заданный момент окончания подготовки системы КПА к проведению испытаний; T ^к – момент окончания подготовки системы КПА к проведению испытаний; T _к ^н , T _к ^к – моменты начала и окончания макрооперации контроля технического состояния системы КПА; T _в ^н , T _в ^к – моменты начала и окончания макрооперации восстановления работоспособности системы КПА; Т к ' н , Т К к - моменты начала и окончания макрооперации контроля после проведения макрооперации восстановления.

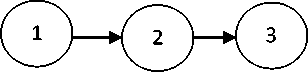
Рис. 3. Модель графа переходов системы КПА:

1, 3 – на системе КПА проводится макрооперация контроля технического состояния системы; 2 – на системе КПА проводится макрооперация восстановления системы КПА

В соответствии с тем что процесс подготовки КПА к проведению испытаний представлен в виде последовательности макроопераций (11), можно записать следую-

щие равенства:
т к = т н + 1 к + 1 в + 1 к ,
ккн T T к       T к ' t к ,
нк тк Т в ,	^             (12)
кн ввв,
нк тв Тк ,
т к к = т н + t K. кк

На основании соотношений (12) запишем систему, позволяющую рекуррентно построить плотность распределения вероятностей момента T к:

Ф_т к ⁽ u ) = Ф_т, к ⁽ u ),

T              ^т к

φ к T к	( u ) = фт, н T к	( u ) ■ Ф z + ( М )
φ н T к	( и ) = Фт к T в	( u ),
φ к T в	( u ) = Фт н T в	( u ) ■ Ф s +( u ),
φ н T в	( U ) = Фт к T к	( u ),
φ к T к	( и ) = Ф + z	( и - Т н ).

( u ),

Выражения (11)...(13) представляют собой математическую модель процесса подготовки системы КПА к про- ведению испытаний, которая включает модели технологических операций контроля и восстановления.

Таким образом, построенная выше система математических моделей позволяет определять момент начала процесса подготовки систем КПА к проведению ЭИ и проводить вычисление вероятности завершения подготовки систем КПА к этому процессу к требуемому моменту времени.

Прогнозная модель технического состояния систем КПА. Задача оценки технического состояния систем КПА на период ЭИ, решаемая при планировании их подготовки к проведению испытаний, представляет собой задачу прогнозирования технического состояния систем, т. е. задачу прогнозирования значений показателей надежности систем КПА для ЭИ КА. Одним из основных этапов при решении этой задачи является выбор или создание модели прогнозируемого объекта.

Если при изучении текущих значений характеристик объекта можно непосредственно исследовать интересующий объект, то при решении задачи прогнозирования необходимо производить выбор или разработку прогнозной модели этого объекта. Анализ объекта прогнозирования включает этапы определения функций объекта, уточнения его структуры и анализа имеющейся исходной информации. При планировании подготовки систем КПА к проведению испытаний объектом прогнозирования являются системы КПА.

В разработанном авторами методе прогнозирования значений показателей надежности процедура получения прогнозной модели осуществляется в два этапа. На первом этапе определяется закон распределения времени безотказной работы систем КПА. На втором этапе полученный закон распределения и модель для расчета значений показателей надежности систем КПА используются для получения аналитической зависимости, с определенной точностью связывающей величину ВБР систем КПА в течение ЭИ с величинами ВБР совокупности элементов КПА, которые обеспечивают выдачу на борт КА конкретных УВ. Полученная зависимость и будет прогнозной моделью систем КПА.

То, что системы КПА являются уникальными системами, объясняет связанный с этим малый объем выборки моментов выявления отказов систем (число наблюдений < 50). С учетом этого обстоятельства для получения закона распределения времени безотказной работы систем КПА был использован метод построения оценки плотности и функции распределения случайной величины по малой выборке. В этом методе определение вида и параметров закона распределения случайной величины состоит из следующих процедур:

• -    вычисления оценок плотности и функции распределения времени безотказной работы системы КПА;

• -    выдвижения гипотезы о виде теоретического закона распределения;

• -    определения параметров принятого теоретического закона распределения по имеющейся выборке моментов выявления отказов системы КПА;

• -    вычисления значений теоретической функции распределения для значений, соответствующих выборке;

• -    проверки сходимости эмпирической функции распределения с принятым теоретическим распределением.

В основе получения прогнозной модели технического состояния системы КПА лежит способ рациональной обработки результатов пассивных многофакторных испытаний. В этом случае под отдельным опытом понимается ЭИ КА, под выходным параметром - вероятность безотказной работы системы КПА при проведении ЭИ КА, под факторами - ВБР совокупности элементов системы, обеспечивающих выдачу конкретных УВ. Значения ВБР системы КПА при проведении ЭИ определяются функцией распределения времени безотказной работы систем КПА, которую строят на основании имеющейся статистической информации об их отказах. Значения ВБР совокупности элементов, обеспечивающих выдачу УВ, получают в соответствии с рассчитанными значениями показателей надежности систем КПА.

Обозначим через R - число ЭИ КА, проведенных за весь период эксплуатации системы КПА. Используя модель для расчета значений показателей надежности систем КПА, для каждого r = 1, ^, R можно определить ВБР совокупности элементов системы КПА, обеспечивающей выдачу j -го УВ, т. е. получить временной ряд изменения ВБР данной совокупности элементов за весь период эксплуатации системы. В итоге получим K' временных рядов. Представим полученные результаты в виде матрицы П размерности K' х R , в которой число столбцов соответствует количеству K' выдаваемых системой УВ, а число строк - количеству R проведенных ЭИ КА:

Р 11 ^Р 12 ... ^Р 1 j ... ^Р 1 К '

П =

^PR 1 ^PR 2 ... ^PRj ... R RK '

На основе закона распределения времени безотказ- ной работы системы КПА получим R значений вероятности безотказной работы системы КПА за время ЭИ КА и представим их в виде матрицы Р:

P c 1

Р =

РсR

Авторами выдвинута гипотеза о том, что аналитическая зависимость, связывающая элементы матриц (14) и (15), имеет линейный характер:

К '

Р с ( t эи ) = Ь о + 2 b j Р ( t j ).            ( ¹⁶ )

j = 1

Вектор B коэффициентов математической модели (16) вычисляется с помощью следующего выраже- ния:

ооо о          В = (ПT ПT )1-1 ПT Р,            (17)

где П T - транспонированная матрица центрированных значений ВБР системы КПА в течение ЭИ КА при выдаче УВ.

Любой j-й коэффициент математической модели можно вычислить по формуле bj = (bp /bj) х

• (    -1 *           - 1 *           - 1 * A ⁽¹⁸⁾

• ^{x ( r} 11 ^r 1 p ⁺ ... ⁺ rij r jp ⁺ ... ^{+ r}RK ' ^rKP X

гд*е rij-1 - элемент обратной корреляционной матриц*ы; rij - коэффициент корреляции между i-м и j-м УВ; rip - коэффициент корреляции между выходным параметром модели Pс(tэ.и) и фактором P(tj):

R

r ^* jр = ( _i Σ_{= 1}[ Р i ( t j ) - Р ( t j )][ Р с i ( t э.и ) -

-

*          Рс(tэ.и)])/(R-1)δ*pδ*j, зд*есь δp – среднеквадратическое отклонение PC(tэ.и), δj – среднеквадратическое отклонение P(tj).

Корреляционная матрица размерностью (K′ + 1)⋅(K′ + 1) составляется из соответствующих коэффициентов корре- ляции. Элементы обратной корреляционной матрицы являются частными от деления алгебраических дополнений элементов корреляционной матрицы на ее определитель. После вычисления значений коэффициентов bj следует проверить точность полученной модели (выдвинутой гипотезы).

Зависимость (16) можно считать прогнозным трендом, устанавливающим зависимость ВБР системы КПА не только от времени, но и от совокупности характеристик системы, т. е. ВБР совокупности элементов системы, обеспечивающих решение задач определенных УВ. А поскольку известно, что если при анализе исследуемого процесса есть основания применить допущения о наличии тренда и об отсутствии в будущем существенных изменений в условиях, определяющих тенденцию развития в прошлом, то процесс экстраполяции заключается в подстановке величины периода упреждения в формулу, описывающую тренд. Таким образом, получение прогноза о значении ВБР систем КПА в течение предстоя- щих ЭИ КА будет заключаться в подстановке в зависимость (16) требуемого периода упреждения.

Представленный в данной статье метод прогнозирования значений показателей надежности позволяет оценивать вероятность безотказной работы систем КПА на предстоящий период проведения ЭИ КА. В основе данного метода лежит модель для расчета значений показателей надежности систем КПА, оценивающая изменение этих показателей от начала эксплуатации до текущего момента времени. Полученный прогноз является основой для принятия решения о необходимости проведения предупредительных мероприятий и распределения их объема и последовательности реализации. Помимо определения объема этих мероприятий, предлагаемый метод позволяет рассчитать объем операций контроля технического состояния, обеспечивающий проверку технического состояния всех элементов систем КПА при оптимально возможном количестве операций контроля.

Непосредственное планирование подготовки систем КПА с определением последовательности операций контроля и предупредительных мероприятий, а также момента начала подготовки систем КПА к проведению испытаний осуществляется на основании модели процесса подготовки систем КПА к проведению испытаний, при которой показатель эффективности этого процесса принимает максимально возможное значение.

На основании всех разработанных моделей и методов создана методика подготовки систем КПА к проведению ЭИ КА.

• V. Z. Voronkovich, P. A. Iosifov

MATHEMATICHAL PROVIDING OF THE PLANNING METHOD OF SUPERVISORY EQUIPMENT SYSTEM PREPARATION FOR ELECTRONIC AND RADIOTESTING OF SPACECRAFTS

The paper is dedicated to the development of model complex of planning for supervisory equipment (SE) system preparation tests, including mathematical model for calculation reliability indexes of SE system and mathematical model of SE system testing process preparation.