Математическое описание диска Эйлера

Указывается, что в настоящее время отсутствует законченная теория диска Эйлера. Приводится полное математическое описание диска Эйлера в статике.

Оглавление

• 1.    Вступление

• 2.    Уравнения состояния

• 3.    Устойчивость диска

• 4.    Выводы

2.    Уравнения состояния

Приложение 1 Приложение 2 Приложение 3 Литература

1.    Вступление

Классическая теория не позволяет объяснить поведение диска Эйлера без привлечения дополнительных сил. В [1] показано, что учет влияния воздуха также не позволяет найти приемлемое движение. Надежда возлагается на влияние трения скольжения, но строгое решение отсутствует, а интуитивные надежды только на это трение мало обоснованы – см., например, [2]. Отсутствует, по-видимому, объяснение перехода от вращения диска вокруг вертикального диаметра к вращению по кругу в наклонном положении. Если диск скользит по окружности, то необходимо, видимо, учитывать еще центробежную силу. Но, главное, что удивляет, - почему диск не падает, а достаточно долго вращается?

Ниже предпринята попытка найти ответы на эти вопросы. Заранее предупреждаем читателя, что ответы получены при том условии, что центробежная сила – это реальная, а не фиктивная, сила. Математическое доказательство этого факта дано в [3]

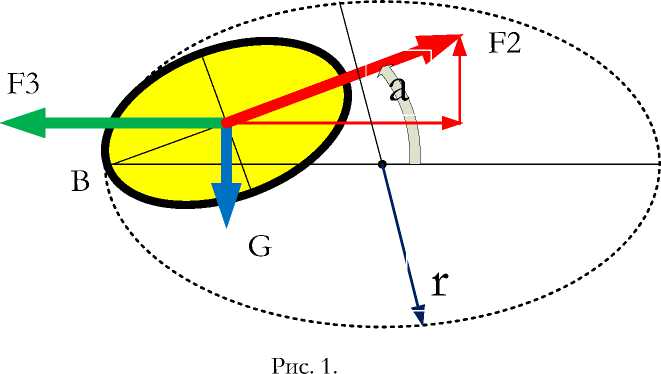
На рис. 1 показан диск Эйлера. В табл. 1 приложения 1 перечислены параметры состояния диска в начальный момент 1 и в момент 2 , когда диск оказывается в положении, при котором угол К <  к(2. Определение этих параметров дано в приложении 1. В момент 1 существует только вращение вокруг вертикальной оси. В момент 2 дополнительно появляется парциальное вращение. Появляется также сила тяжести ту , вектор которой проходит мимо точки вращения О. Из-за этого появляется уменьшение потенциальной энергии волчка

W_P = ту^(1 — sin к)                        (1)

• -    см. формулу или (п2.7) в приложении 2.

  

Запишем для момента 2 уравнения законов сохранения импульса L и энергии W , которые не зависят от того, каким образом и какими силами диск перешел в это состояние:

L2 + L4 = Li,(2)

W2 + W4 + WP = W1.(3)

Подставляя уравнения из табл. 1 в уравнения (1, 2), получаем:

/2^2 + /з°з = /1^1,

4/2^2 + 4/3^2 + Wp = 4/2^2.(5)

где - 60 1 , 60₂ - угловые скорости вращения волчка в момент 1 и 2, 60 3

• -    угловая скорость парциального вращения. Из (4) находим:

3.    Устойчивость диска

°з = л(2 °1 - °2)'

Подставляя (6) в (5), находим:

4/2^2 + 4/3 (^Q<1-«^ + Wp - 4J<2t. (7) В приложении 1 показано (см. (п2.9) в приложении 2), что WP — qj 2<3 (8) где q — константа - см. (п2.10) в приложении 2. Из (7, 8) получаем: 4/2^ + 4/з^2 + q^/2^2 — 4/2^2 (9) Обозначим а — J3 (10) b — (1 + 4qa). (11) Тогда из (9, 10, 11) получим: асо2 + bco2 — а<2. (12) Из (10, 6, 12) найдем асо2 + b(<)A — <2)2 — ааУ2, (13) или (b + а)со2 — 2bco1co2 + (b — а)со2 — 0, (14) Решая (14), получаем: ^2 — ТГ^- (b ± а). 2 (b+a)v      у (16) Из экспериментов следует, что <2 ^ «1. Тогда (b-a) ^2 —     7^1. 2   (ь+а 1 (17) Из (6, 17) находим: ( 1           \ a(3a-b) <3 — а(2<1   <2) — 2(b+a) <01. (18) Из (18) найдем 2(b+a) <1           <3. 1    a(3a-b) 3 (18а) а из (18а) и (17) найдем (b—a) 2(b+a)         2(b—a) <2                <3           <3. 2   (b+a) a(3a-b) 3   a(3a-b) 3 (18b) Диск переходит в наклонное положение под действием силы тяжести тд. Преобразование этой энергии в кинетическую энергию вращательного движения волчка происходит благодаря т ому, что в процессе падения на него, как известно, действует сила Кориолиса F1, которая создает крутящий момент и соответствующую ему угловую скорость прецессии <3.

Падению волчка противодействует, как известно, еще одна сила Кориолиса F2. Диск падает очень медленно. Это означает, что сила F2 примерно равна силе тяжести — см. приложение 2. Очевидно, при таком торможении источник этой силы расходует энергию, примерно равную Wp. Следовательно, для этой силы существует источник энергии. Но этому предположению мешает устойчивое современное представление о том, что сила Кориолиса — фиктивная сила. А фиктивная сила не может доставлять энергию…

В приложении 2 показано, что при некотором ^=^_о сила Кориолиса 1*2 уравновешивает горизонтальную центробежную силу F 3 и вертикальную силу тяжести тд — см. (п2.3) и (п2.5).

До достижения этой скорости диск постепенно падает под действием силы F₄ , определяемой из (п2.6а) и вычисляемой как результат взаимодействия силы Кориолиса и силы тяжести. При F 4 = 0 процесс падения останавливается. Но для этого диск должен начать падать.

При К= 0 видно, что F₄ = тд . Но эта сила направлена вертикально и не может вызвать падения. Таким образом, для начала падения внешняя сила должна вывести его из вертикального положения.

4.    Выводы

Итак, действие сил Кориолиса приводит к тому, что

• •    диск при падении теряет кинетическую энергию, полученную при пуске, но восполняет ее за счет потенциальной энергии;

• •    существует такое наклонное положение диска, при котором сила Кориолиса уравновешивает горизонтальную центробежную силу и вертикальную силу тяжести;

• •    в таком положении кинетическая энергия диска сохраняется неизменной и равной кинетической энергии, полученной при пуске;

• •    падение диска из указанного устойчивого положения вызвано постепенным уменьшением его кинетической энергии за счет торможения;

• •    медленное падение диска обусловлено торможением за счет второй сила Кориолиса, которая должна для этого расходовать энергию (подобно тормозному двигателю спускающегося спутника),

Такое действие этих сил Кориолиса и центробежных сил возможно только в том случае, если они могут совершать работу, т.е. являются реальными силами. Это доказывает реальность этих сил. С другой стороны, математическое доказательство этого факта дано в [1]. Там показано, что эти силы могут быть обоснованы как следствие уравнений Максвелла для гравитомагнетизма, а источником энергии для этой силы является гравитационное поле Земли. Но и в отсутствии такого доказательства существует множество сомнений в утверждении о том, что указанные силы являются фиктивными [2].

В приложении 2 показано, что из уравнений диска следует неравенство т > R. Моделирование показывает, что при т > R существует некоторый угол К, где все параметры состояния диска принимают бесконечное значение. Таким образом, всегда выполняется условие т = R. (19)

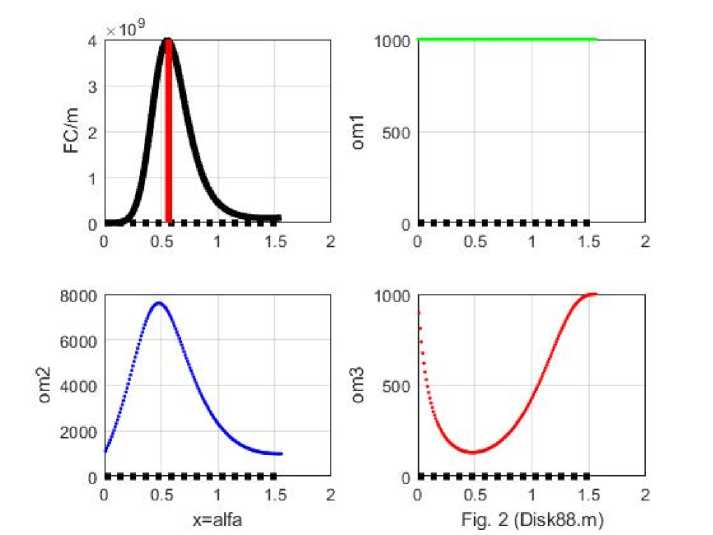
Приведенные уравнения позволяют найти все параметры волчка при данном и R. В табл. 1 приведены некоторые примеры в системе СИ. Далее показаны графики функций 0)1, О₂, 0)₃ и удельной силы Кориолиса F₂/m при 0 1 = 1000 и R = 0.25 — см.

рис. 2. Видно, что существует резкий максимум при К~ ТТ/2 , где сила Кориолиса принимает наибольшее значение. В этой точке диск надолго задерживается в устойчивом состоянии — см. рис. 3 из [5].

Рис. 3.

Приложение 1

Здесь мы определим параметры состояния волчка в моменты 1 и 2. В табл. 1 приведены основные формулы, где приняты следующие обозначения

К - угол наклона диска к плоскости качения, т - масса диска, д — ускорение земного притяжения, тд - сила тяжести,

R - радиус диска,

• h - высота центра диска - см. рис. 1,

• 0)1 - угловая скорость вращение диска вокруг вертикального диаметра в момент 1,

• 0)2 - угловая скорость вращения диска вокруг вертикального диаметра в момент 2,

О з - угловая скорость парциального вращения в момент 2,

• V - линейная скорость прецессии,

• L - момент инерции,

• / - момент импульса, W — энергия.

Таблица 1.

	Угловая скорость	Момент инерции	Момент импульса	Кинетическая энергия
Вращение диска вокруг собственной вертикальеой оси	( 1	/1 = ^mR 2	L1 = /1< У 1	W 1 =2 L i ( i2 1     , = 8 А( 2
Вращение диска, наклоненного под углом К к плоскости, вокруг собственно оси	( 2	1     7 / 2 = 2 mR2	L2 = /2(2	W 2 =2 L 2 ( 2 1      2 = 4 /2(2
Парциальное движение волчка, наклоненного под углом К к плоскости.	( 3	/з = / 2 + mR2 (теорема Штейнера) /3 = C • mR 2 , где C = 1.5
			1       2 L3 = /з ( з = ~mR ( 3
				W 3 = 2 L 3 ( 3 = 1      2 = 4 /з(з = 1      . . = —mR2( 2

Из рис. 1 следует:

h = Rtg(K).                                       (п1.0)

Из табл. 1 следует:

CL = — = 1/1.5,                              (п1.1)

/з                                                                4     7

Линейная скорость прецессии — это скорость движения т. В на радиусе АВ, вращающемся с угловой скоростью (3 (см. рис. 1):

• V = <У3(г - RcOs(k)).                       (п1.3)

Приложение 2

Падению волчка противодействует, как известно, сила

Кориолиса

F2 = —2m(2 х V,                               (п2.1)

где V - линейная скорость прецессии (п1.3), и центробежная сила

F3 = -т(2(г — RcOS(K))                   (п2.2)

В установившемся режиме сила F 3 и сила тяжести тд уравновешиваются силой F 2 . — см. рис. 1. Поэтому из (п.2.1, п2.2, п1.3) находим:

Fl

F2 = - “3^ = ™w2 (г - ЯсобСк))/б1пСк),      (п2.4)

тд = —F2cos(к) = тсо2(г — Rcos(к)) - ctg(к)      (п2.5)

или

д = ш^ (^—cos(к)) ■ ctg(^).                       (п2.6)

Если это равенство не выполняется, то диск падает под действием силы, определяемой из ( п2.5 ):

F4 = тд — то>2(г — Rcos(к)) • ctg(^)              (п2.6а)

Видно, что решение этого уравнения существует только при

Г >  R .                                            (п2.6 а ).

Следователно для диска Эйлера всегда выполняется условие (п2.6 а ).

При наклоне на угол к диск смещается по вертикали на R(1 — sin к) и, следовательно, теряет потенциальную энергию

WP = mgR (1 — sin к).

( п2.7 )

Совмещая эту формулу с (п2.6), находим:

WP = m^R (j — cos(K)) ctg(K)(1 — sin к).   (п2.8)

Далее совместим эту формулу с формулой для J 2 из табл. 1. Тогда найдем:

Wp = i^m^R2 (j — cos(K)) ctg(K)(1 — sin к).

или

(п2.9)

(п2.10)

^WP = ^qJ2^w3

где

q = 2 (" cos(к)^ ctg(к)(1 — sin к).

Приложение 3

Здесь мы подробнее рассмотрим силу Кориолиса F 2 , определенную по (п2.1):

F2 = 2mto2to3oo2R (j — cos(x)),               (п3.1)

Из (п3.1, 18b) найдем

F = -2m3 ^g^,       (п3.2)

Далее из (п3.1, 18b) найдем

2nZ v , \ 2 2(b -a) 2 2(b + a) V

F2 = -2ma)2R — — cos(^) 02 ——---— ——---tt

• ^{2          3} \R ^v J ¹ a(3a — b) \a(3—-b)J

или

F2 = — 2m(j02Ra.f,                                 (п3.3)

где

af = 2 (R - cos(«>) (b -a)(b + a)2 I / 3 j; ! (п3.4)