Математическое описание функциональных преобразований сигнала с угловой модуляцией в последовательно соединенных квантователях фазы и напряжения

Для формирования сигналов с угловой модуляцией (УМ) используют цифровые синтезаторы сигналов (ЦСС). В зависимости от типа ЦСС с УМ используется как раздельное, так и совместное квантование фазы и напряжения [1–3]. При квантовании могут использоваться два способа: округление и усечение [4-6]. На рис. 1, а-б изображены передаточные характеристики квантования, соответствующие операции округления, а на рис. 1, в – операции усечения.

Рассмотрим функциональные преобразования сигнала с УМ в квантователе напряжения с передаточной характеристикой, соответствующей операциям усечения и округления первого и второго типов.

Ступенчатая функция Н ( x ), описывающая нелинейную передаточную характеристику квантователя, имеет точки разрыва 1-го рода. Для её аппроксимации аналитическими функциями можно использовать метод, в основе которого лежит представление нелинейной функции в виде контурного интеграла [7]

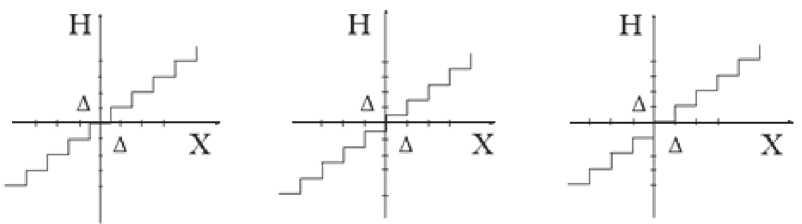
а

б

в

Рис. 1

H (x) = — [ F (js) ejxsds, 2n i где

^

F ( js ) = J H ( x ) e - jxs dx .

-^

Решение задачи можно упростить, сводя интегральные преобразования (1) и (2) к ряду Фурье. При этом передаточные характеристики квантователей трех рассматриваемых вариантов, соответствующих операциям округления первого, второго типов и операции усечения, можно представить соответственно в виде:

Тогда выражение (6) можно преобразовать к виду

Uфu (t) = Uocos{Hф [ф(t)]} +

2 U

+ —0

~

У -1-sm

M i

(N L ^{- 1} ) cos { H ф [ф ( t ) ]}) .

В свою очередь, с помощью оператора квантования фазы, соответствующего операции усечения,

U ^ф( t ) = U « s nr MM^cos И ^{t )-п /} M ]+

. Д^( - 1 ) m • 2 2 п   )

H ( x ) = x +—> -——sin    mx ;

n ^M m I A J

”

+ Х U 0

m = 1

sin n ( mM ± 1 ) / M п ( mM ± 1 ) / M

A^, 1 . 2 2 n   )

H ( x ) = x +—> —sin     mx ;

n ^M m V ^{A J}

X COs { ( ^mM ± 1 ) [ф ( t ) -k / ^M ] } ,

H ( x )

A A 1 . 2 2 n   )

= x ---1— M —sin I — mx I ,

² К m = 1 m V ^A    J

из выражения (8) получим

где Δ – шаг квантования.

Математическое описание сигнала с квантованной фазой и напряжением можно получить с помощью операторов квантователей фазы Н _φ и напряжения Нu :

sin n /M

^{U ф} u ⁽ t ^{) =} U 0 - M cos [ ^ф( t ^{) + П} / ^M ] ⁺

■A sinn( mM ± 1)/ M

+ U E7(     ) ^x

⁰ h n ( mM ± 1 ) / M

U , u ( t ) = H u^ U o cos { H , [ф ( t ) ] }/       ( 6)

Оператор квантования напряжения, соответствующий операции округления первого типа (3), имеет вид

( -1V   2 2 п

^{u (} ) = ^{+ M} nV A" J ^,

x cos { ( mM ± 1 ) [ф ( t ) -n / M ] } +

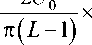
x

гор h , sln(^(LL- 1)cos{Hф[ф(t)]}/.

г - 1   ^

где Д _u = 2 U 0 / ( L -1) - шаг квантования напряжения; U ₀ – амплитуда исходного сигнала с УМ; L – количество уровней квантования напряжения.

Первое слагаемое в (10) описывает основную составляющую сигнала с квантованной фазой и напряжением, второе слагаемое - дополнительные составляющие, обусловленные квантованием сигнала с УМ по фазе, а третье слагаемое - составляющие, обусловленные квантованием по напряжению сигнала с квантованной фазой. Однако

Том 2

получить запись третьего слагаемого в (10) в явном аналитическом виде в данном случае затруднительно. Выражения, близкие по структуре к (10), имеют место и в случае, когда передаточная характеристика квантователя фазы соответствует операции усечения, а передаточная характеристика квантователя напряжения соответствует операциям округления второго типа и усечения [8, 9]. Для преодоления этих трудностей напрямую воспользуемся методом отображения сигналов, сущность которого состоит в следующем [10]. Неравномерно дискретизированный сигнал с УМ из области определения отображается в область изображений таким образом, что в ней уже имела место равномерная дискретизация сигнала с УМ. После этого исследуют функциональные преобразования сигнала с УМ и квантовой фазой, используя для этого известные результаты, полученные для равномерной дискретизации и интерполяции, а затем осуществляется обратное отображение.

Тогда получим отображение сигнала с квантованной фазой и напряжением ф

U ф u ⁽ t Н U Ф u ^(v) / ^{ф (v)} •

В соответствии с отношением эквивалентности

. f [ф( t)] ~ f (v) / Ф/ (v)

образ сигнала (6) имеет вид

Uфu (v) = UФu (v) / Ф/ (v).

U;.M = Hu {cos[H„W]}, и представляет собой косинусоидальную функцию с квантованной фазой и напряжением.

Процесс квантования фазы и напряжения гармонического сигнала в области изображения представлен графически на рис. 2. Поскольку фаза такого сигнала ф ( ф ) изменяется по линейному закону, то длительность всех ступенек квантованного сигнала одинакова. Поэтому сигнал U _Ф и (ф) можно рассматривать как результат последовательно проводимых операций: дискретизации сигнала U ₀cosф эквидистантной последовательно^стью ™^а-фун™^й.

y (ф- ,Z»fr-r ».)■ квантования амплитуды дискретных отсчетов и ступенчатой интерполяции.

Дискретизированный и квантованный гармонический сигнал можно описать выражением

м

U дк ( v ) = S U r ⁵ ( v ^- r ^А ф ) .       (14)

r =-м

где амплитуда отсчетов Ur в зависимости от способа квантования напряжения определяется:

- при использовании операции округления первого типа (рис. 1, а )

тт    2Uo 1

U =---0 ent r L -1 I

L -1    / x

.    os ⁽ r ^А ф ^{) +} 0.5

;

- при использовании операции округления второго типа (рис. 1, б )

U r

2 U 0

L - 1

ent

L — 1

cos ( r А_ф ) + 0,5 ^ ;

при использовании операции усечения (рис. 1, в )

Ur =

2 U 0

L -1

ent

L—¹ cos ( ^{r А} ф ) ^{+ 0,5}

А u 2^,

где ent( x ) – операция выделения целой части числа.

Сигнал U _дк(ф) является периодическим с периодом повторения ф₀ = М А_ф. В связи с этим спектр его также представляет собой дискретную периодическую функцию, интервал между соседними спектральными линиями которой Z 1 = 2п/ф₀ = 1, а период повторения по оси Z равен Z , = 2п/ф₀ = М . Значения коэффициентов дискретного преобразования Фурье (ДПФ) определяются из выражения

.      1 M ^{- 1}      - J 2^- kr

Ck = — У U_re M .

^k   2n r z^   r

Ступенчатую интерполяцию сигнала U _дк(ψ) можно представить в виде свертки U д _к(ф) ® g ₀(ф), где g ₀(ψ) для квантователя фазы с передаточной характеристикой, соответствующей операции усечения, представляет собой прямоугольный импульс вида

g о ( ф ) =

f ¹, ⁰ ^v < ^A . ;

_ 0, ф <0, ф>А_ф ,

спектральная плотность которого определяется выражением

G o ( Z ) =

^{Sin ZA} y / ² e-jZA^/2

^{Z /2}

В этом случае коэффициенты C_k сигнала U _{φ u} (ψ) можно определить из произведения

■

Ck =

sin ^{( n k /} M ) e -з п k / m n k / M

M ^{- 1}

1 Ue m r:^

2 n

^{- J}M1'

^ . (19)

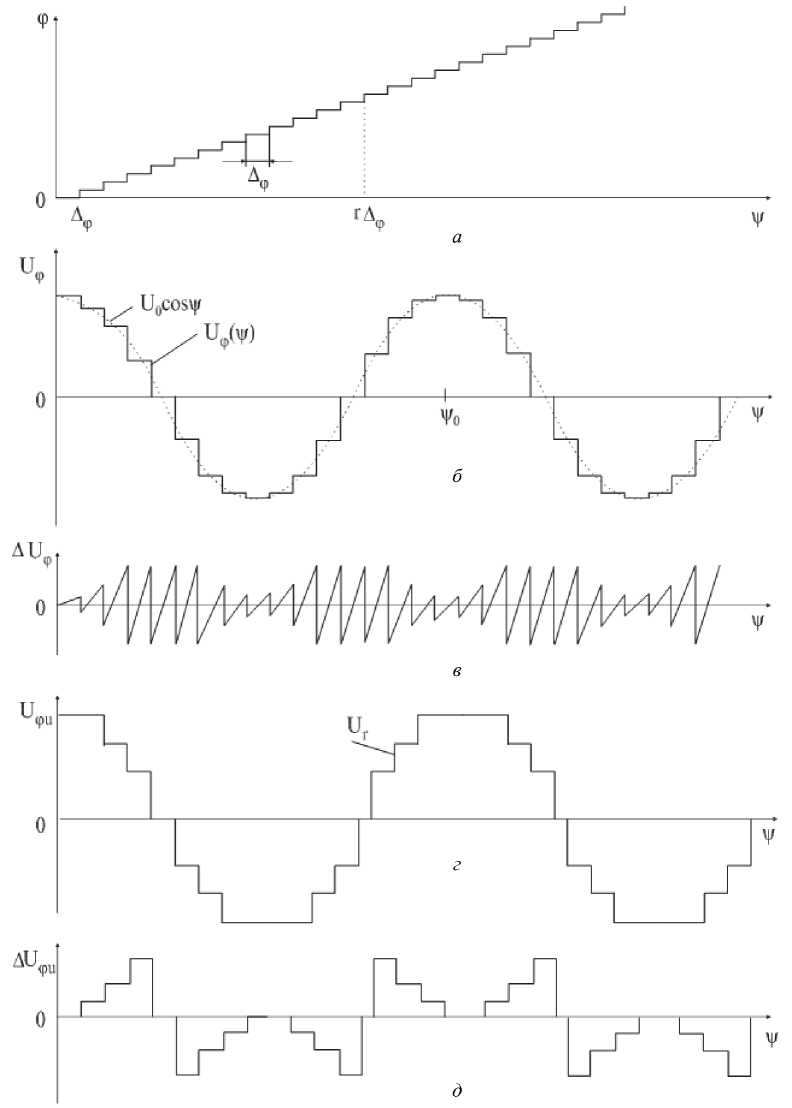
Рис. 2

Сначала рассмотрим ситуацию, когда передаточная характеристика квантователя напряжения соответствует операции округления первого и второго типов. В этом случае, как видно из (15) и (16), амплитуды r -го и ( r + M /2)-го дискретных отсчетов U_r одинаковы, а их полярности разные. Поэтому по аналогии со спектром сигнала с УМ, квантованного по напряжению, спектр сиг

нала U ^ u ( у ) содержит только нечетные составляющие

■

2 к - 1 =

sin |\ ( 2 к ^- 1 ) / M ] e _ j ^ к — 1 ) / м _х п ( 2 к - 1 ) / M                  (20)

1 M - ¹      - j —л ( 2 к - 1 ))

х — ? U_re ^м ’

M &  r

.

Том 2

Тогда сигнал U^u (у) можно представить рядом Фурье: - ифu (у) = Z U2k-icos[(2k - 1)v-n(2к -1)/M] (21)

^где U 2 к - 1 = ² | C 2 к - 11 •

Подставляя (21) в (12) и осуществляя обратное отображение Θ : U (ψ) → U ( t ) в соответствии с отношением эквивалентности (11), получим

U,u (t) = U1COS[ф(t)-п/M] + то

+ Z и 2 к - , cos [ ( 2 к - 1 ) ф ( t ) -п ( 2 к - 1 ) / M ] • (22) к = 2

В выражении (22) первое слагаемое описы

вает основную составляющую сигнала с квантованной фазой и напряжением, которая имеет такую же фазовую структуру, что и исхо дн ый сигнал с УМ. Второе слагаемое описывает дополнительные нечетные составляющие сигнала с квантованной фазой и напряжением. Их полный фазовый угол в (2 k – 1) раз больше, чем полный фазовый угол φ( t ) исходного сигн ала с УМ. П оскольку п ри квантовании фазы используется операция усечения, то сигнал с квантованной фазой и напряжением имеет постоянный фазовый сдвиг, пропорциональный номеру составляющей π(2 k – 1)/ М .

Рассмотрим теперь ситуацию, когда передаточные характеристики кван тователя напряжения, как и квантователя фазы, соответствуют операции усечения. В этом случае для коэффициентов ДПФ сигнала U ^ u ( у ) , учитывая (17) и (18), получим следующее выражение:

C k

= <

Sin ( ^{п к} / ^M ) e_ j „ к / M п к / M

^ч(пк M) e _jnк / m пк / M

\ M - 1

Ф у

2 м ^:

e

2 п

M

>•

Первое слагаемое в (23) аналогично выражению (19), а второе слагаемое равно Δ _u /2 при к = 0 и равно нулю при остальных значениях к . Тогда, учитывая (23) и производя преобразования, аналогичные используемым при выводе выражения (22), для последнего рассматриваемого случая получим:

UФи ( t ) = U1cos [ф( t )-n / M ] + то

+Е U^k icos [(2 к - 1)ф( t )-п( 2 к -1) / M ]

к=2

где U _{2 k} - 1 = 2 С _{2 kч} , а коэффициенты ДПФ С 2 _{к -1} определяются из (20) и (16).

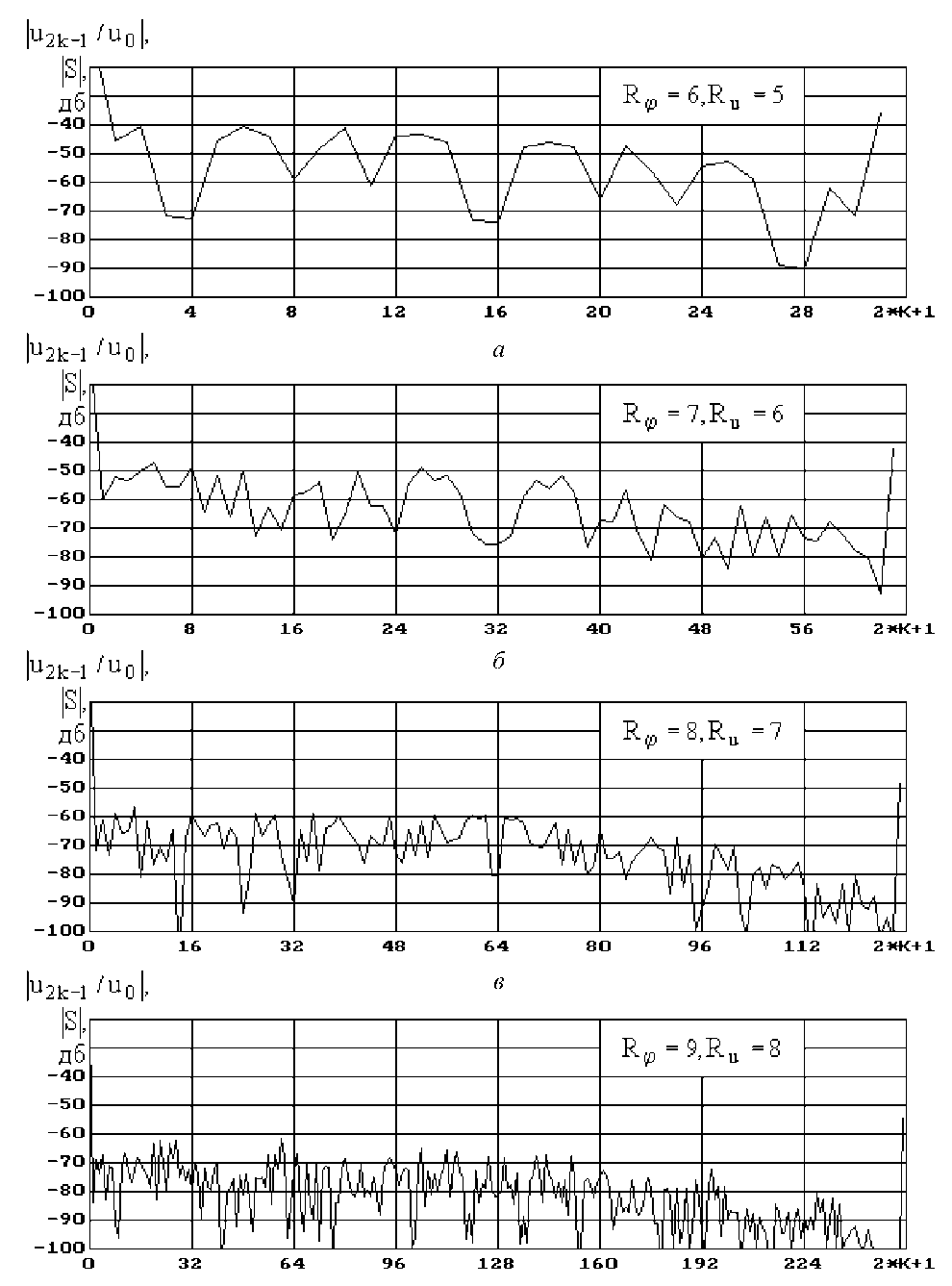
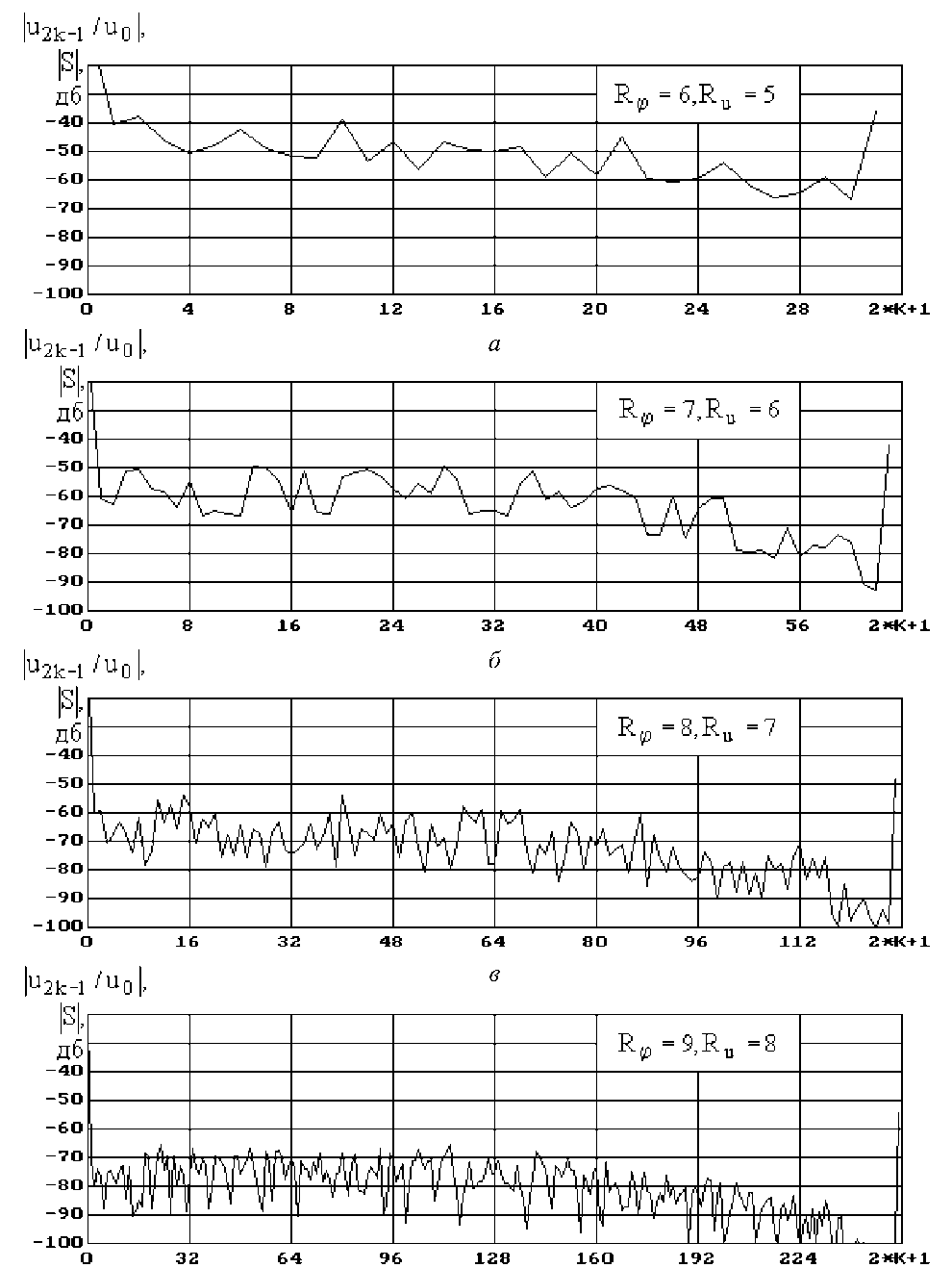
На рис. 3 в логарифмическом масштабе изображены нормированные значения амплитуд нечетных составляющих сигнала с квантованной фазой и напряжением U 2 _{к -1}/ U 0 в зависимости от значения k , рассчитанные в соответствии с выражениями (20) и (15), для различных числа разрядов квантования фазы R _φ и напряжения R_u .

На рис. 4 приведены аналогичные зависимости, рассчитанные в соответствии с выражениями (20) и (16), также указаны нормированные значения амплитуды основной составляющей сигнала с УМ с квантованной фазой и напряжением U 1 /U 0 .

Сопоставляя выражения (24) и (22), с учетом (16), (19), (20) и (23) нетрудно убедиться, что при использовании операции усечения для квантования фазы и напряжения аналогичные графики будут отличаться от графиков, изображенных на рис. 3, только постоянной составляющей, равной Δu/2. Как следует из (10) и (22), (24) и наглядно видно на рис. 3 и 4, дополнительные составляющие сигнала с УМ с квантованной фазой и напряжением можно разделить на два вида. Первые из них, имеющие индекс mM ± 1, представляют собой дополнительные составляющие, обусловленные квантованием фазы сигнала с УМ. Их полный фазовый угол в mM ± 1 раз больше, чем у исходного сигнала с УМ, а амплитуда пропорциональна значению sin[π(mM ± 1)/M] / [π(mM ± 1)/M].

Вторые из них, имеющие индекс 2к - 1, обусловлены квантованием напряжения сигнала с УМ с квантованной фазой. Эти составляющие, как видно из (20), в зависимости от их номера имеют амплитудную модуляцию в виде sin[π(2k – 1)/M] / [π(2k – 1)/M].

Максимальное значение этих составляющих не превышает половины шага квантования напряжения.

Резюмируя все вышесказанное, можно сделать следующие выводы:

• -    полученные аналитические выражения описывают функциональные преобразования сигналов с УМ в последовательно соединенных квантователях напряжения и фазы с использованием методов контурного интеграла и отображения сигналов;

• -    полученные математические модели функциональных преобразований сигналов с УМ в последовательно соединенных квантователях фазы и напряжения позволяют использовать их для анализа структуры спектров и для аналитических расчетов искажений спектров и корреляционных функций этих сигналов.

г

Том 2