Математическое описание трехуровневого преобразователя частоты с фиксированной нейтралью на базе активного выпрямителя и автономного инвертора напряжения

В течение последнего десятилетия отечественные и зарубежные промышленные предприятия оснащаются современными системами реверсивных электроприводов большой мощности (РЭП БМ), которые имеют в своем составе высоковольтные многоуровневые преобразователи частоты различных топологии [1–3]. Основными факторами, способствующими их распространению, являются, с одной стороны, возможность обеспечения высокого качества потребляемой электроэнергии и энергоэффективности, а с другой – ужесточение отечественных и международных стандартов к электромагнитной совместимости и энергосбережению [4–6]. Из всего разнообразия рассматриваемых топологий преобразователей трехуровневые преобразователи частоты с фиксированной нейтралью (3У-ПЧ с ФН) на базе активных выпрямителей (АВН) и автономных инверторов напряжения (АИН) наиболее часто встречаются в системах РЭП БМ [7–9].

Несомненно, при математическом моделировании и анализе различных режимов работы РЭП БМ существует необходимость в разработке математического описания 3У-ПЧ с ФН на базе АВН и АИН, что является сложной задачей, требующей знаний о его принципе работы, алгоритмах модуляции и систем управления. Известные математические модели 3У-ПЧ с ФН [10–12], основанные на принципе разделения электрической системы на подсистемы, не позволяют получить удобные математические модели для синтеза систем управления. Другой известный метод построения математических моделей силовых полупроводниковых преобразователей, основанный на матричном представлении объекта [13–15], показал свою применимость для двухуровневых топологий с точки зрения синтеза системы управления, однако по отношению к 3У-ПЧ с ФН данный метод не был рассмотрен. В настоящей статье поставлена задача создания математической модели 3У-ПЧ с ФН на базе АВН и АИН, позволяющей синтезировать систему управления и учитывать совместную работу АВН и АИН.

Описание объекта исследования

3У ПЧ с ФН на базе АВН и АИН состоит из 24 полностью управляемых полупроводниковых ключей VT 1 – VT 24 , 24 обратных диодов VD 1 – VD 24 , 12 фиксированных диодов VD c 1 – VD c 12 , снабберных цепей C S 1 – C S 12 , R S 1 – R S 12 и двух эквивалентных емкостей С_{dc 1} и С_{dc 2} (рис. 1) [16–18]. На рис. 1 были использованы следующие обозначения: u – напряжение, В; i – ток, А; abc – трехфазная неподвижная система координат; αβ – двухфазная неподвижная система координат; dq – двухфазная вращающаяся система координат; 1–24 – порядковые номера; r – АВН; v – АИН; l – нагрузка; f – фильтр; dc – звено постоянного тока; T – трансформатор.

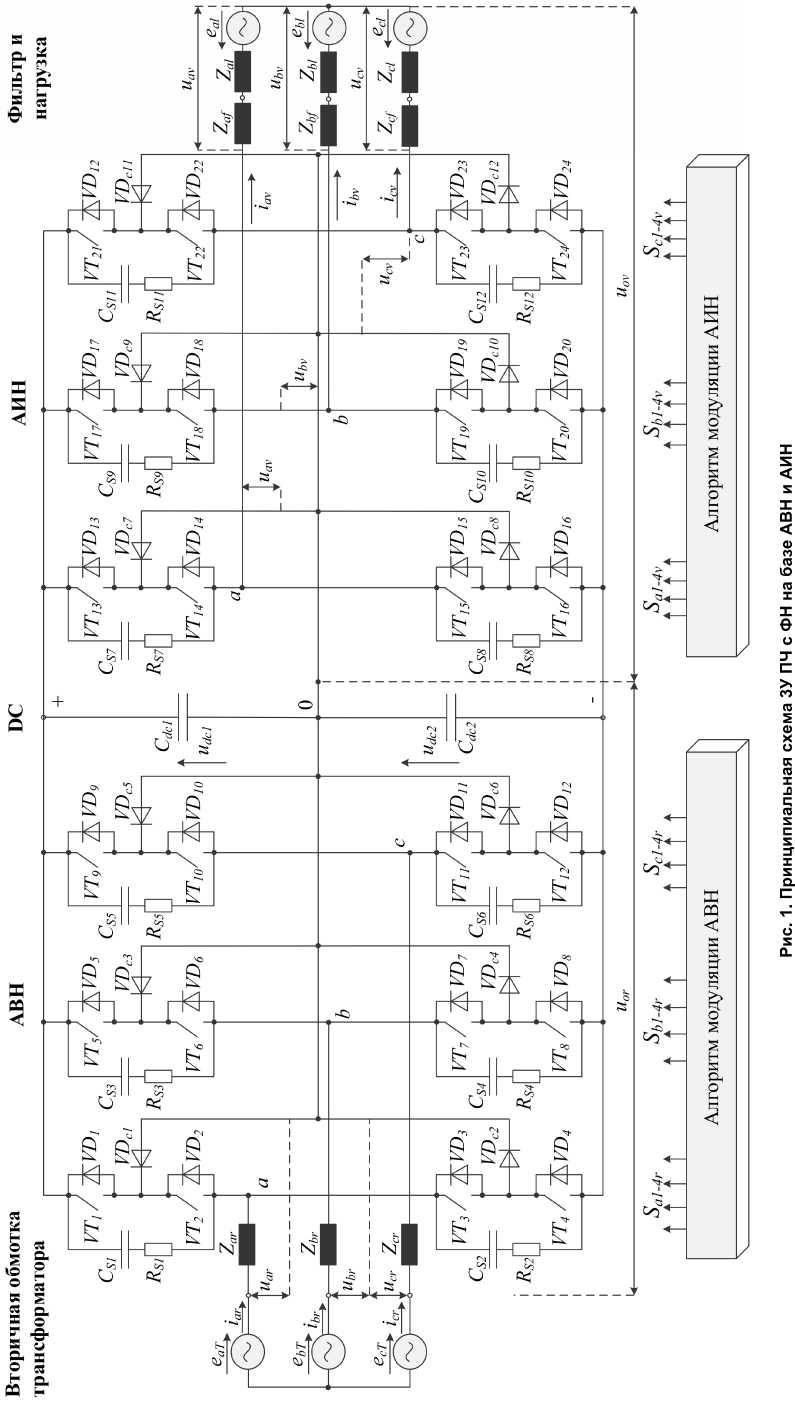
Из 4 ключей в каждом плече моста (рис. 2) одновременно могут быть включены только 2, подключающие потенциалы u dc к фазе нагрузки в трех точках «+» , «0» и «–» [19–21]. Различные комбинации подключения u dc в каждом плече моста формируют три состояния фазных напряжений преобразователя: [P] – подключение к положительному полюсу «+», [O] – подключение к нейтральному полюсу «0» и [N] – подключение к отрицательному полюсу «–».

Выходное фазное напряжение формируется в виде прямоугольных импульсов с уровнями + u dc /2, 0 и –u dc /2 (рис. 3).

u dc1

u dc2

С dc1

VT 3

С dc2

VD 2c

VT 4

P

VD 1

VT 1

VD 1c

VT 2

VD 2 i a <  0

u dc1

С dc1

VT 1

VD 1

VT 1

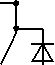
VD 1c

VD 1c

u dc1

С dc1

VT 2

VT 3

С dc2

u dc2

VD 2c

VT 4

i a >  0

VD 3

VD 4

VD 4

N

i a >  0

i a <  0

VD 3

VT 3

u dc2

С dc2

VD 2c

VT 2

VT 4

O

VD₂ i a >  0

i a <  0

Рис. 2. Пример формирование фазного напряжения для плеча 3У ПЧ с ФН

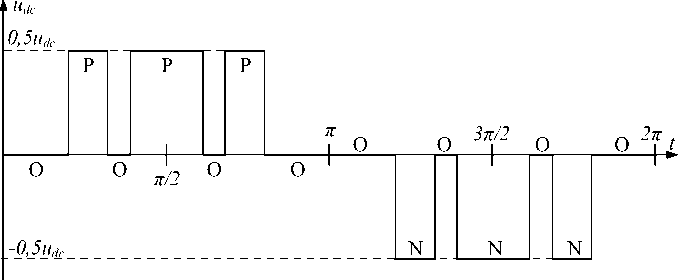
Рис. 3. Типовая форма выходного фазное напряжение для плеча 3У ПЧ с ФН

Разработка математической модели

За основу построения математической модели 3У ПЧ с ФН (см. рис. 1) были приняты дискретные ло- гические функции, описывающие состояния полупроводниковых приборов. Для АВН:

1, ^ ⁽ S abc 1 r и S abc 2 r ) = ¹ и ⁽ S abc 3 r и S abc 4 r ) = 0

^Y abcr = 1 0, ^ ⁽ S abc 2 r и S abc 3 r ) = ¹ и ⁽ S abc 1 r или S abc 4 r ) = 0 •

[- 1, ^ ⁽ S abc з r и S abc 4 r ) = 1 и ⁽ S abc 1 r и S abc 2 r ) = 0

Для АИН:

1, ^ ⁽ S abc 1 v и S abc 2 v ) = ¹ и ⁽ S abc 3 v и S abc 4 v ) = 0

^Y abcv = | ⁰ ’ ^ ⁽ S abc 2 v и S abc 3 v ) = ¹ и ⁽ S abc 1 v или S abc 4 v ) = 0 •

^ ^— 1, ^ ⁽ S abc 3 v и S abc 4 v ) = ¹ и ⁽ S abc 1 v и S abc 2 v ) = 0

Затем, были использованы дискретные логические функции, зависящие от состояний проводимости двух верхних и двух нижних полупроводниковых ключей в каждом плече моста АВН и АИН:

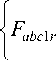
^Y abcr ^(y abcr ⁺ 1) .

2          ’

F к abc 2 r

Y abcr ( Y abcr 1 )

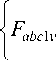
^Y abcv ^(y abcv ⁺ 1) .

2          ’

P _ Y abcv ( Y abcv 1 ) Fabc 2 v =

Вторичная обмотка трансформатора представлена в виде трехфазного источника напряжения с внутренним активно-индуктивным сопротивлением. При разработке математической модели были приняты следующие допущения: активно-индуктивное сопротивление сети является симметричным Z_aT = Z_bT = Z_cT ; трехфазная система ЭДС трансформатора симметрична и имеет синусоидальный характер изменения с постоянной амплитудой и постоянной частотой e_aT + e_bT + e_cT = 0.

Трехфазная электрическая нагрузка и фильтр представлены в виде трехфазного источника напряжения с внутренним активно-индуктивным сопротивлением. При разработке математической модели были приняты следующие допущения: трехфазная электрическая нагрузка является симметричной Zf = Zbf = Zf; Zai = Zbl = Zci; трехфазная система ЭДС симметрична и имеет синусоидальный характер изменения с переменными амплитудой и частотой eal + ebl + ecl = 0; схема имитирует соединенную в звезду обмотку двигателя.

Используя данные допущения и уравнения равновесий напряжений и токов, полученные с помощью первого и второго законов Кирхгофа, составлена система уравнений, описывающая электромагнитные процессы ЗУ ПЧ с ФН на базе АВН и АИН, в следующем виде:

<

u abcT = u abcr ⁺ i abcr ■ Z abcr ;

uabcl = uabcl ⁺ i abcv ■ ^{( Z} abcf ⁺ Z abcl ) ^;

u abcr = udc 1 ■ D abc 1 r ⁺ udc 2 ■ D abc 2 r ;

u abcv = u dc 1 ■ D abc 1 v ⁺ u dc 2 ■ D abc 2 v ^;

u dc 1 =

⁽ F a 1 r ■ i ar ^{+ F}b 1 r ■ i br

■ i cr ) — ⁽ F a 1 v ■ i av ^{+ F}b 1 v

u dc 2 =

^{( F}a 2 r ■ i ar ^{+ F}b 2 r ■ i br

C dc 1 ■ Р

■ i cr ) ⁽ F a 2 v

■ i bv ^{+ F}c 1 v ■ i cv )

;

C dc 2 ■ Р

■ i av ⁺ F b 2 v ■ i bv ^{+ F}c 2 v ■ i cv )

,

в которую добавлены следующие обозначения:

Г 1 ь . c       ^ г

D abc 1 r = 1 F abc 1 r       J j F n 1 r I , D abc 2 r = 1 F abc 2 r

\                 и = л /                 v

_

1 b . c

1 ^ F n 2 r

-^ и = л

Г                      1      b . c i                           Г

Dabc 1 v   I Fabc 1 v   ~  ^J Fn 1 v I, Dabc2v   I Fabc2v v                 и= л /                 v

_

i     b . c

— У F.

~ n 2 v

-^ и = л

В связи с периодическим изменением во времени токов и напряжений, уравнение (5) целесообразно преобразовать из неподвижной системы координат [ abc ] во вращающуюся систему координат [ dq 0]. Для этого мгновенные значения токов и напряжений в системе (5) сначала преобразуются в неподвижную систему координат [aeY] путем применения преобразования Кларка, посредством которого обеспечивается инвариантность амплитуд, а составляющая y = 0:

x a

xb

2 Г Л ■ x_b Л ■ x_c ) j x ^e = 3 -[  --- 2- J^;

x Y = 0.

После [aeY] преобразования коммутационные функции F и D в системе (5) становятся равными, так как исчезают межфазные мультипликативные связи. В качестве примера представлен переход из системы [ abc ] в [aeY] для коммутационных функций F_a i _r и D_a i _r :

к - ² U F a1 r = з I Fa 1 r

^Fb 1 r ^Fc 1 r

2 2

Dal r = ²

^a 1 r    3

b . c

- 1 ■ ! F n

-J и = /r

1 --■

b.c n1r

³ n = a

3 I F

-

b 1 r

-

c 1 r I _ 77

2 1“ F a1 r .

Затем мгновенные значения токов и напряжений были преобразованы во вращающуюся систему координат [ dq 0] с ориентацией по вектору напряжения питающей сети для АВН и произвольного вектора для АИН таким образом, чтобы вектор напряжения сети и нагрузки по оси q был равен нулю. Координатное преобразование [αβγ]/[ dq 0] осуществлялось посредством следующего математического выражения:

X d = X a ' COS ( ^ю t ) + X p ' sin ( ^ю t ) ; x q = - x _a ' sin ( ^ю t ) + X p ■ cos ( ^ю t ) ; ^x 0 = °.

После применения преобразования (8) система (5) приняла следующий вид и была использована для построения структурной схемы (рис. 4):

u dT    u dr ⁺ i dr ■ Z dr

® T ■ Z qr ■ i qr ;

⁰ “ u qr ⁺ i qr ■ Z qr ⁺ ® T ^- Z dr ■ i dr ;

u dl    u dv + i dv " ⁽ Z df + Z dl )

® l ■ ( Z qf ⁺ Z ql ) ■ i qv ;

⁰ = u qv

u dr . u qr u dv u qv

“ u dc 1

' qv ■ ( Z qf ⁺ Z ql ) ⁺ ® l ‘ ( Z df ⁺ Z dl ) ^- i dv ; ■ ^Fd 1 r ⁺ u dc 2 ■ ^Fd 2 r ^;

“ u dc 1 ■ ^Fq 1 r ⁺ u dc 2 ■ ^Fq 2 r ;

“ u dc 1 ■ ^Fd 1 v ⁺ u dc 2 ■ ^Fd 2 v ;

“ u dc 1 ■ ^Fq 1 v ⁺ u dc 2 ■ ^Fq 2 v ^;