Математическое описание вентильного индукторного генератора с конденсаторным возбуждением
Автор: Воронин Сергей Григорьевич, Чернышев Алексей Дмитриевич
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Электромеханические системы
Статья в выпуске: 1 т.20, 2020 года.
Бесплатный доступ
На волне развития транспортных средств на электрической тяге сильный толчок получило и развитие автономных энергетических установок. К новым техническим решениям относится представленная энергетическая установка на базе индукторной машины с новым принципом возбуждения фазных обмоток. В основу его заложена такая особенность подобных электрических машин, как возможность обеспечения трапецеидальной формы фазных ЭДС, что позволяет осуществлять коммутацию и возбуждение фазных обмоток в естественном режиме без необходимости отслеживания и коммутации фазных токов в зависимости от положения ротора, за счет коммутации конденсаторов неработающей фазы. Такое решение позволяет значительно упростить и снизить стоимость электронной аппаратуры управления вентильного индукторного генератора. В силу новизны конструкции рассматриваемое техническое решение не было исследовано ни зарубежными, ни отечественным учеными. В данной статье осуществлено математическое описание работы и разработана математическая модель вентильного индукторного генератора с конденсаторным возбуждением, которая позволяет вычислять токи и ЭДС как в электрической машине, так и во внешней электрической схеме, а также величину крутящего момента. В статье представлены результаты расчетов и экспериментальных исследований разработанного генератора, совпадение которых в достаточной мере подтверждает адекватность модели. Разработанная модель позволяет наглядно исследовать электромагнитные процессы, работоспособность и функционирование системы в различных режимах при разнообразных внешних воздействиях, отрабатывать алгоритмы управления и оценивать энергетические показатели генератора, а также может служить основой для создания методики проектирования и создания новых установок.
Автономная энергетическая установка, электрическая машина, вентильный индукторный генератор, математическая модель
Короткий адрес: https://sciup.org/147234035
IDR: 147234035 | УДК: 621.313.1 | DOI: 10.14529/power200112
Текст научной статьи Математическое описание вентильного индукторного генератора с конденсаторным возбуждением
При разработке новых автономных энергетических установок большой интерес вызывают вентильные индукторные генераторы с самовозбуждением (ВИГ или SRG), что подтверждается их применением в качестве тяговых генераторов транспортных средств с комбинированной энергетической установкой. Этому способствуют такие достоинства ВИГ, как управляемое электромагнитное возбуждением, пассивный ротор, концентрические катушки фазных обмоток, охватывающие по одному зубу статора, простая конструкция и высокая технологичность изготовления электрической машины [1–4].
Данные машины обладают рядом недостатков, которые сдерживают более широкое их распространение, в том числе необходимость применения асимметричного полумостового преобразователя на IGBT-транзисторах, большого количества датчиков и довольно сложной системы управления с контролем фазных токов в зависимости от положения ротора. Все это усложняет систему в целом и увеличивает ее конечную стоимость, приравнивая к стоимости классического решения на основе синхронных генераторов с постоянными магнитами или электромагнитным возбуждением [5–11].
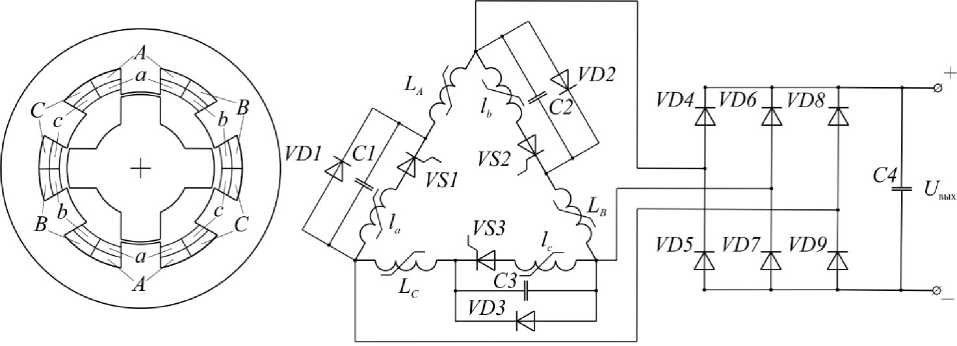
В настоящей статье рассматривается новое схемно-конструктивное решение, позволяющее значительно упростить и снизить стоимость электронной аппаратуры управления ВИГ [12, 13]. В основу его заложена такая особенность подобных электрических машин, как возможность обеспечения трапецеидальной формы фазных ЭДС, что позволяет осуществлять коммутацию и возбуждение фазных обмоток в естественном режиме без необходимости отслеживания и коммутации фазных токов в зависимости от положения ротора. На рис. 1 приведен простой вариант такой конструкции на основе трехфазной электрической машины с одной парой полюсов
На рис. 1: A , B , C и a , b , c – совмещенные якорные и дополнительные обмотки фаз генератора; LA , LB , LC и la , lb , lc – собственные индуктивности
а)
б)
Рис. 1: а – магнитная система; б – электрическая схема нового ВИГ
якорных и дополнительных обмоток; VD 1– VD 3 – шунтирующие диоды; VS 1– VS 3 – тиристоры в цепи возбуждения; C 1– C 3 – конденсаторы возбуждения; VD 4– VD 9 – диоды силового выпрямителя; C 4 – конденсатор силового выпрямителя; U вых – напряжение на выходе выпрямителя генератора.
Математическое описание электромагнитных процессов в подобной конструкции ввиду ее новизны отсутствует, и для его осуществления рассмотрим сначала ее принцип действия.
Принцип действия нового ВИГ
Представленное решение (см. рис. 1) – вентильный индукторный генератор с конденсаторным возбуждением (ВИГ КВ) – заключается в отделении от якорных обмоток A , B , C дополнительных обмоток возбуждения a , b , c , которые совместно с конденсаторами C 1– C 3 и полупроводниковыми компонентами в виде шунтирующих диодов VD 1– VD 3 и тиристоров VS 1– VS 3 образуют цепь возбуждения. В процессе работы дополнительные обмотки la , lb , lc осуществляют заряд конденсаторов C 1– C 3, которые при выходе фазы, параллельно которой включены, из такта генерации вырабатывают значительный импульс тока. Формируемый импульс тока за счет соединения обмоток в многоугольник протекает по всем якорным обмоткам L A , L B , L C , тем самым возбуждая фазу, находящуюся в такте генерации [12]. Тиристоры VS 1– VS 3 позволяют с высокой точностью осуществлять регулирование выходного напряжения U вых за счет изменения соотношения между полупериодами тока, пропускаемых ими, и полупериодов напряжения, прикладываемого к ним [13].
На рис. 2 представлены идеализированные диаграммы индуктивностей, токов и ЭДС-фазы. Здесь условно выделены 4 участка, соответствую- щие характеру изменения индуктивности. Первый участок характеризуется практически постоянным минимальным значением индуктивности, в это время происходит коммутация между фазами, не представленными на рис. 2. Второй участок характеризуется практически линейным ростом индуктивности. Рассматриваемая фаза не вырабатывает электрической энергии. Третий участок соответствует полному перекрытию зубцов статора и ротора с практически постоянным максимальным значе- нием индуктивности, после этого момента начинается возбуждение рассматриваемой фазы, что осуществляется с помощью цепи возбуждения (конденсатора) предшествующей фазы. Четвертый участок характеризуется уменьшением эквивалентной площади перекрытия зубцов и линейным уменьшением индуктивности, на данном участке происходит генерация электрической энергии.
В соответствии с рис. 2 на основании общепринятого допущения [14–17], изменение как собственной, так и взаимной индуктивности фазы можно описать укороченным рядом Фурье:
( L=L o + Lmcos(9+^(k j -1)y,
(M = Mo + Mm cos( 9 + ^ (2(kj + kj±.) - 1)), ( где L – индуктивность обмотки; L0 = 0,5(Ld + Lq) – постоянная составляющая индуктивности обмот- ки; Lm = 0,5(Ld – Lq) – переменная составляющая индуктивности обмотки; Ld – индуктивность об- мотки в согласованном положении; Lq – индуктивность обмотки в рассогласованном положении; θ – угол поворота ротора в электрических градусах; m – количество фаз электрической машины; M – взаимная индуктивность обмоток; M0 = 0,5(Md + Mq) – постоянная составляющая взаимной индуктивности обмотки; Mm = 0,5(Md – Mq) – переменная составляющая взаимной индуктивности обмотки; kj и kj±1 – порядковые номера фаз электрической машины.
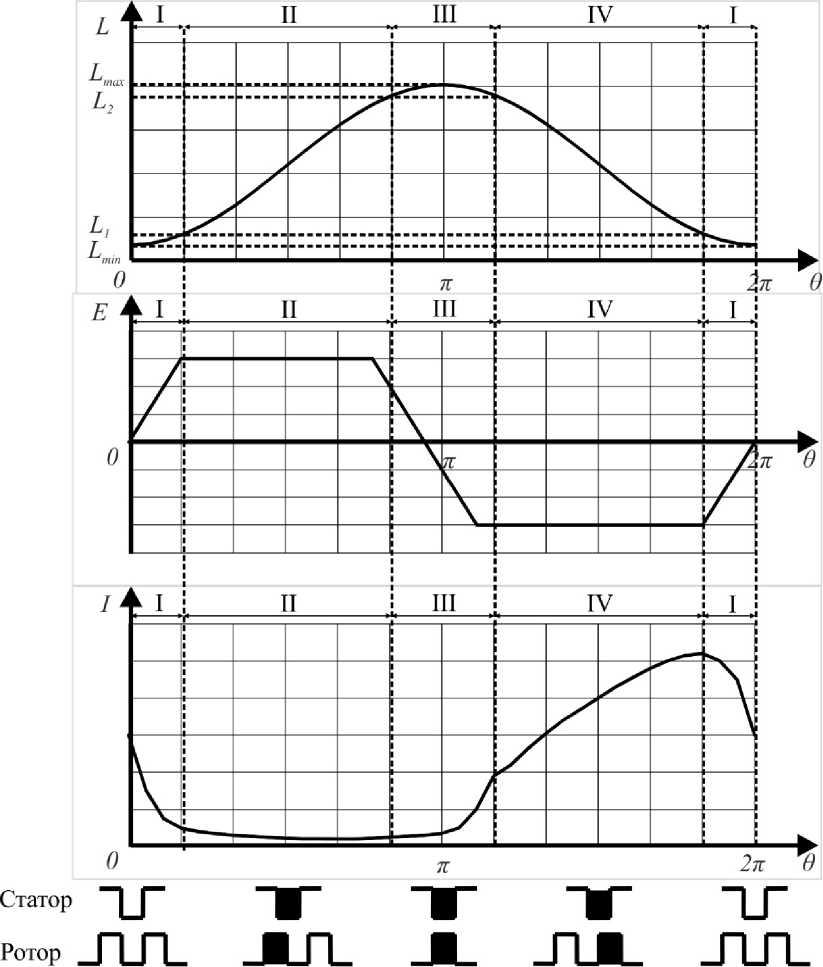
Рис. 2. Ток, ЭДС и индуктивность фазы ВИГ КВ
Математическое описаниеэлектромагнитных процессов ВИГ КВ
Математическое описание электромагнитных процессов ВИГ КВ представляет собой трудоемкую задачу, обусловленную нелинейностью процессов, происходящих в электрической схеме, как из-за сложной магнитной системы электрической машины, так и из-за наличия довольно большого количества электронных и электрических компонентов схемы [18]. Для описания электромагнитных процессов электрическая схема генератора, работающего на активную нагрузку, в соответствии с теорией цепей [19, 20] представлена эквивалентной схемой (рис. 3).
На рис. 3 обозначено: LA, LB, LC, la, lb, lc – собственные индуктивности обмоток якоря и возбуж- дения; r и rд – активные сопротивления обмоток якоря и возбуждения; C1, C2, C3 – емкости конденсаторов цепи возбуждения; rдиф1–rдиф3 – эквивалентные дифференциальные сопротивления тиристоров цепи возбуждения; rдиф4–rдиф6 – эквивалентные дифференциальные сопротивления шунтирующих диодов цепи возбуждения; rref1–rref6 – эквивалентные дифференциальные сопротивления диодов выпрямителя; R – активное сопротивление нагрузки; IA, IB, IC и ia, ib, ic – токи силовых обмоток фаз; IC1, IC2, IC3 – токи возбуждения, формируемые конденсаторами; IR – ток активной нагрузки, взаимные индуктивности обмоток на рис. 3 не указаны. Эквивалентные дифференциальные сопротивления rдиф1–rдиф6 и rref1–rref6 описывают работу полупроводниковых компонентов, и их можно
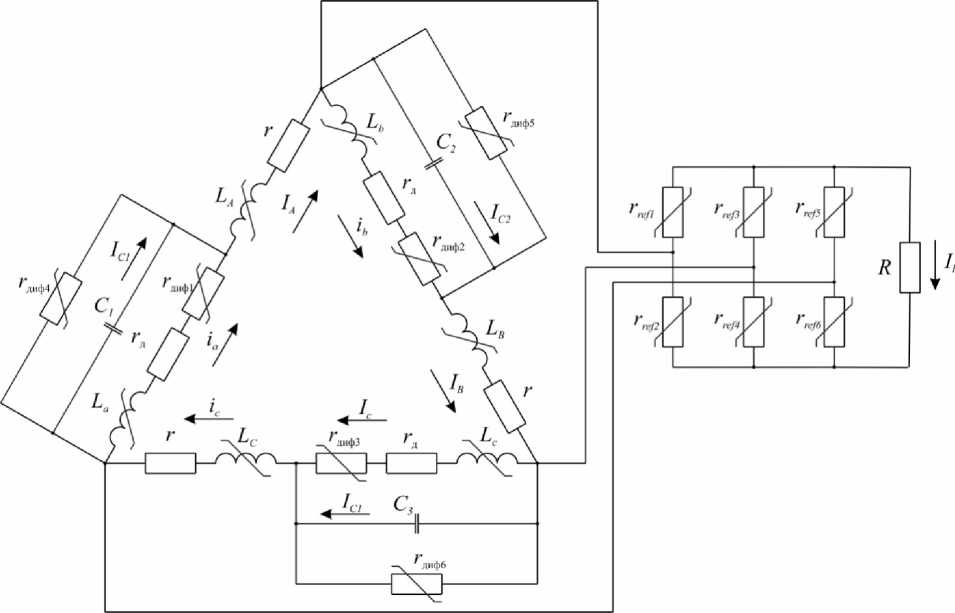
Рис. 3. Эквивалентная электрическая схема ВИГ КВ
представить как функции от напряжений якорных ( UA , UB , UC ) и дополнительных ( ua , ub , uc ) обмоток, прикладываемых к ним, и токов дополнительных обмоток и токов управления ( ig ) [21, 22]: r диф1 = f ( i a , i g ); r диф2 = f ( i b , i g ); r диф3 = f ( i c , i g ); r диф4 = f ( u a ); r диф5 = f ( u b ); r диф6 = f ( u c );
r ref 1 = f ( U A , U B ); r ref 2 = f ( U A , U B );
r ref 3 = f ( U B , U C ); r ref 3 = f ( U B , U C );
r ref 4 = f ( U B , U C ); r ref 5 = f ( U A , U C );
r ref 6 = f ( U A , U C ).
Безусловно, такие зависимости, основанные на кусочно-линейной аппроксимации, являются довольно грубыми с точки зрения силовой электроники и не описывают всех процессов, происходящих в полупроводниковых компонентах, а значит, могут давать значительные погрешности, особенно в моменты коммутации. Это особенно явно при больших значениях шага интегрирования, по этой причине при численном интегрировании был выбран шаг, значительно меньший электрических постоянных времени полупроводниковых компонентов.
Для упрощения описания электрическую схему (см. рис. 3) целесообразно разделить на несколько более простых в соответствии с рабочими тактами и состояниями полупроводниковых элементов. Всего рабочих тактов 6, одна половина из них соответствует режиму коммутации, а другая половина – процессу генерации электрической энергии ими. Примем за начальное положение ротора согласованное положение зубцов статора и ротора для фазы А, в таком случае описание начинается с прекращения генерации фазой С и возбуждения фазы А, участок 3 (см. рис. 2). Эквивалентная электрическая схема для данного процесса представлена на рис. 4, где условные обозначение компонентов те же, что и на рис. 3: IA_1, IB_1, IC_1 и ia_1, ic_1 – токи силовых обмоток фаз для первого такта, IC1_1, IC3_1 – токи возбуждения формируемый конденсаторами для первого такта, IR_1 – ток активной нагрузки для первого такта. Описание электромагнитных процессов электрической схемы (см. рис. 4) представлено в виде двух систем уравнений напряжений (2) и (3). Такое разделение необходимо для упрощения решения и осуществляется с точки зрения суперпозиции, при этом система дифференциальных уравнений (2) исключает из решения цепь с конденсатором возбуждения C1, а система дифференциальных уравнений (3) исключает из решения цепь с конденсатором возбуждения C3. Значения токов IA_1, IB_1, IC_1, ia_1, ic_1, IC1_1, IC3_1, и IR_1 находятся путем сложения соответствующих токов, полученных при решении систем дифференциальных уравнений, т. е.
IA _1 = IA _11 + IA _12, IB _1 = IB _11 + IB _12, IC _1 = IC _11 + IC _12, Ia _1 = Ia _11 + Ia _12, Ic _1 = Ic _11 + Ic _12, IR _1 = IR _11 + IR_ 12, I C 1_1 = I C 1_12 , I C 3_1 = I C 3_11 .
За начальное условие примем некоторое значение скорости вращения ротора ω и напряжение на конденсаторах возбуждения U c 10 , U c 20 , U c 30 .
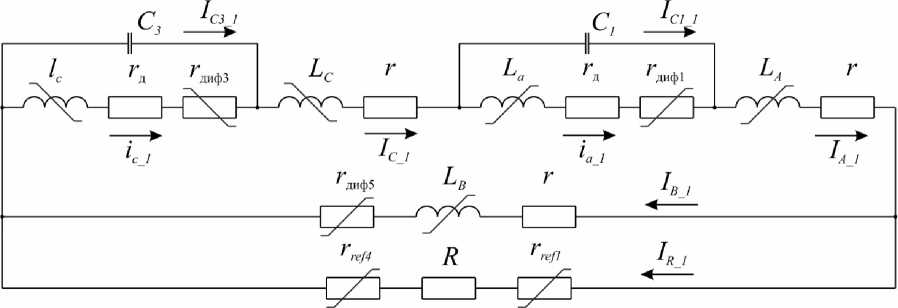
Рис. 4. Эквивалентная электрическая схема работы ВИГ КВ на первом такте
^ C3_11 + (гдифЗ + rg) i c_11 + ^d-11 = 0; d^c d^C d^ail .
+ (гдифЗ + Гд) ! Сц + ^T1 + Г/^ 11 + ^T1 +
= 0;
+ (гдиф1 + rd) ia _11 + ^^T1 + Г 7Л _11 + dddt-1 - + (гдиф 5 + г) 7 в_11
^^£и+(г +rjic +^^^и + г/с +^ + dt дифЗ д С11 dt L11 dt
|
+ (гдиф1 + Гд ) ^ a_11 |
+ 55^ + г/ 4_11 + (е |
+ Гге/1 + Гге/4) ^ й_11 0; |
|
" i c 11 + / c и |
= 0; |
|
|
^ 4_11 — ^ B11— ^ B11 |
= 0; |
|
|
< |
^ 4 11 = ^ C 11; |
^^в
(
+ d^ a 12
+ d^ c i2 dt
^ C1_12
+ (гдиф1 + Гд) 1а _12
^^ + (гдиф 3 + Гд ) ic _12
dt
+ Г ^ С_12
= 0;
। d^ a i2 । ' dt
+ (гдиф1 + Г К 12 + ^^Г2 + Г /л _12 + ^^dL12 + (гдиф 5 + г) / в_12
= 0;
d^ C_ 12 d^ C = 12
dt + (ГдифЗ + Гд )lC_12 + dt + Г,С_12
+ (гдиф1 + Гд )la _i2
+ d^ 4 12
dt
£ d^ C1 12
+ Г ^ 4_12
к
dt ^ 4_12
—
^B.
^^в
^12 '
. 12 —
+ ( R + r re/ i + ^ 4_12 = 0; ' ^Я_12 = 0;
^ 4_12 = ^ C_12 .
^^в
+ d^ C 12 | dt
+ Гге/4) ^ й_12
= 0;
Второй такт (рис. 5) работы системы представляет генерацию электрической энергии фазой А , участок 4 (см. рис. 1). На рис. 5 условные обозначения компонентов те же, что и на рис. 3: IA _2, IB _2 и ia _2 – токи силовых обмоток фаз для второго такта; I C 1_1 – ток, формируемый конденсатором C 1 для второго такта; IR _2 – ток активной нагрузки для второго такта. Описание электромагнитных процессов электрической схемы (см. рис. 5) представлено в виде системы уравнений напряжений (4). В данном случае по якорным обмоткам фаз B и С течет один и тот же ток IB _2 = IС _2.
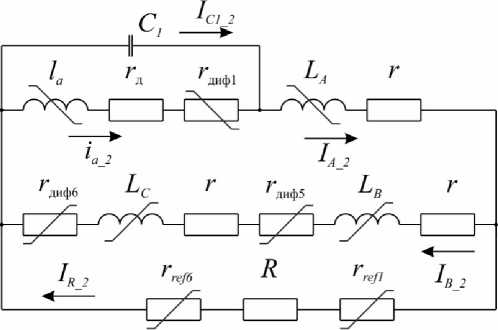
Рис. 5. Эквивалентные электрические схемы работы системы
^ C1_2 + ( ' диф1 + ' И'.' 2 + 77-^ = 0;
7^ + ( ' диф1 + Г д )ia_2 + 77^ + rIA_2 + 77^ + ( ' диф5 + r)lB 2 +
+ Т^Э + (r + ГДиф6)1С2 = 0;
Tjp + (гдиф1 + гд) 1 а_2 + 77U + rIA2 + (R + rref1 + rref6)lR_2 = 0;
C dUc-^ dt
IA_2 - IB.
ia 2 + IA_2 = 0; .2 - IR_2 = 0;
V
IB_2 = IC_2 .
Входящие в системы дифференциальных уравнений (2)–(4) ψA, ψB, ψC и ψa, ψb, ψc – полные магнитные потокосцепления силовых обмоток фаз генератора и дополнительных обмоток фаз генератора, в общем случае можно выразить:
AAa _ La- ia + Mab ■ ib + mac ■ ic + MAa ■ ia ;
Ab _ Lb ■ ib + Mba ■ ia + Mbc ■ ic + мвь ■ V;
Ac = Lc ■ IC + Mca ■ IA + Mcb ■ IB + MCc ■ ic;
A a = La-ia + M Aa ■ I a ;
A b = Lb ■ ^ b + MBb ■ IB;
I A c = Lc ■ ic + M c c ■ I c .
Для того чтобы использовать для решения этих уравнений численные методы [20–23], представим их в матричной форме:
5I = A -1 (-B)X. (6)
С учетом (5) матрицы переменных входящих в (6) для системы дифференциальных уравнений (2)–(4) будут равны:
|
" Uc3_11" |
vU c1_12" |
Г U c1_2" |
|||
|
X 11 _ |
i c 11 I C_11 |
; X12 = |
i a 12 I a_12 |
; X2_ |
i a 2 I a_2 |
|
VI b11 \ |
VI b 12 J |
VI b 2 J |
|||
-
a12_11 _ lc; a13_11 _ MCc" ; a22_11 _ lc + MCc; a23_11 _ LA + LC + la + 2MAa + MCc + 2MAC + MBC + MAB" ;
-
^ 24 11 = LB + MAB + MBC; ^ 32 11 _ lc + MCc"; ^ 33 11 _ LA + LC + la + 2MAa + MCc + 2MAC;
-
a34_11 _ MAB + MBC; a12_12 _ la; a13_12 _ MAa; a22_12 = la + MAa;
-
^ 23 12 = LA + LC + lc + MAa + 2MCc + 2MAC + MBC + MAB; ^ 24 12 = LB + MAB + MBC; __
-
a32_12 = la + MAa; a33_12 = LA + LC + lc + MAa + 2MCc + 2MAC; a34_12 = MAB + MBC" ;
^ 12 2 = la; ^ 13 2 = MAa; ^ 22 2 = la + MAa; ^ 23 2 = LA + MAa + MAC + MAB;
a24_2 = LB + L c + MAB + 2MBC + MAC; a32_2 = la + MAa; a33_2 = La + MAa; a34_2 = MAB + MAC;
коэффициенты матрицы B в зависимости от такта:
Ь 21_11
Ь33ц ^ 34_11
Ь43ц
Ь 44_11
Ь 22_12
Ь 33_12
Ь 34_12
Ь 43_12
Ь 44_12
d e. dM cc d £.i_ dM cc
' диф 3 + Г д + dt ; ° 22_11 dt ; ° 32-11 dt + dt + Г д + Г диФ 3;
= dl A + dl c + di a + 2 dM A„ + dM C£ + 2 dM AC + dM BC + dM AB + 2 r + r - . .
dt dt dt dt dt ^t dt ^t д диф1'
dLB dMAB. dMc -^c.^CMcc dt + dt + dt +Г + ГдиФ5; °42_11 dt + dt +Гд +ГдиФ3;
= tiL ^ + tiL c + tii ^ + 2^ + ДМсс + -2^ ^ ml+ 2г + гл + гдиФ1 + R + rTen + rTef4;
dt dt dt dt dt dt д диф 1 re>1 rel4’
_ dMAB dMBC _ _ Яа, dt + dt R rref1 rref4; °21_12 гдиФ1 + rg + dt ’
_ dM Aa l _ di a 1 dM Aa . .
= dt ; ° 32_12 = dt + dt + r g + г диф 1;
-
-
-
_
_
_ dL A 1 dL C 1 di c 1 dM Aa 1 2 dM Cc 1 2 dM AC + dM BC + dM AB + 2r + r + r "
_ dt dt ^t dt dt dt dt ^t д диф 3;
_ dL B dM AB .dM BC _ da. dMAa. r . .
dt + dt + dt +Г + Г диФ5 ; ° 42_12 dt + dt +Г д + Г диФ 1;
_ d^ + d^ + di, + dM^ + 2 ^cc + 2 ^^ +2r + r+ гиФЗ + R + rTen + rTef4;
dt dt ^t dt dt dt д диф 3 re>1 rel4’
_ 5M aB + dM B c r -
dt
5t
rre/1
-
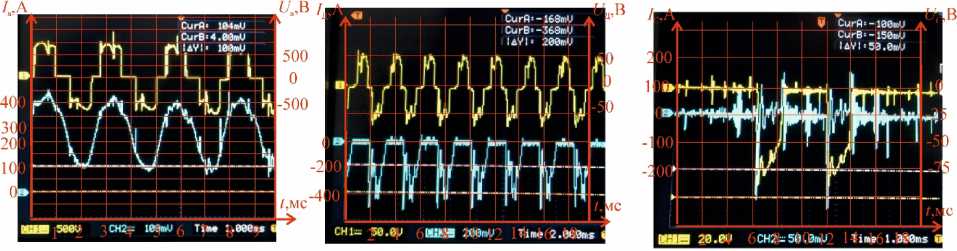
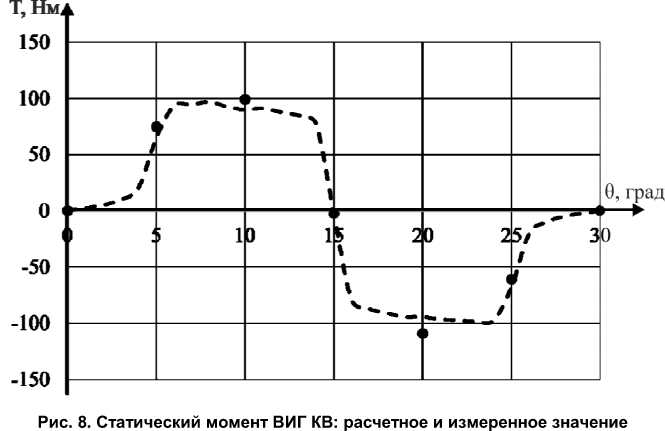
da. _ 'ref4; u12_2 = 'диф1 +'д +dt ; U12_2 = dt ; =Ш^+<»^^,+ т 6 dLl+dMA«+JMu: +JM«+T. 2- dt dt д диф1' 23_2 dt dt dt dt , _ OL^ OLc .йМдв9 OMbc , Mac , 9„ , „ h °а , йМда . ”24 2 dt + dt + dt + 2 at+ dt +2+ Гдиф5 + Гдиф6' Й32_2 dt + dt +тд + Гдиф1' °33_2 —dt+dt+ T + R +'refl+ TTef6> °34_12 = dt+dtK 'refl 'reff>. Оставшиеся токи для решаемой системы дифференциальных уравнений не составляет труда найти, используя следующие выражения: ^R_11 = ^C_11—^Вц; ia_11 = Za_11 = ^C_11; Ir__12 = Ia_12—^B_12; ic_12 = Za__12 = ^C__12; Ir_2 = ^4_2 —^В_2; ^В_2 = ^C_2. Так как циклы работы повторяются, то системы уравнений для последующих тактов могут быть записаны аналогичным образом со сдвигом фазы. Вектором начальных условий для системы дифференциальных уравнений нового такта является вектор значений токов и напряжений после решения предыдущего интервала. Переход между тактами осуществляется по углу поворота ротора в соответствии с интервалами, представленными на рис. 1. Общее решение находится путем припасовывания каждого отдельного решения к предыдущему. Электромагнитный момент ВИГ КВ Вращательный момент на валу электрической машины T можно представить как сумму моментов, создаваемых k-й якорной обмоткой Tk и k-й дополнительной обмоткой Tдk [14]: rn Т —Lk=1 Т + Тдк, где 1 d^ 1 d^ *k 2ik de’ 1дк 2igk de . С учетом (2) выражение (7) можно представить в виде: fТ — ^h (h^ + ^^ + Ib0^ + Ic 4 2 4 X4 de a de В de C Tb = ^Ib(I/Jlb + 1 °^+ d^ + 2 В \ В de D de 4 deC Tc -2Ic(Ic T 1 a t ^+icdM£c + i OMac + i de c de 4 de В — ^iteJ^ + i^J^y. 2 a \ a de 4 de J — lihtih^ + ifiMsbX. 2 ° \ ° de В de J d^); dMBC^ . dMBc) . V Tc-1ic(ic — + Ic—). c 2 c\c de C de J Завершающим уравнением, описывающим ВИГ КВ, является второй закон Ньютона для вращательного движения: .^=Т J dt - Tl , где TL – момент нагрузки; J – момент инерции приведенный к ротору. Оценка адекватности математических моделей Конкретные расчеты были проведены на основе взаимосвязанного решения девяти систем дифференциальных уравнений. Их интегрирование в матричной форме проводилось методом трапеции по специально разработанной программе на ЭВМ в программно-вычислительном комплексе Scilab. В качестве примера был взят разработанный и изготовленный опытный образец ВИГ КВ мощностью 132 кВт на производственных мощностях ООО НПП «Резонанс» для применения в электромеханической трансмиссии сельскохозяйственного трактора. Следует отметить, что погрешность интегрирования в разработанной модели в соответствии с известным выражением (10) составляет не более 0,002 [24, 25], что, по мнению авторов, является достаточной точностью для данной модели с учетом принятых допущений, в том числе представления полупроводниковых компонентов в виде дифференциальных сопротивлений, основанных на кусочнолинейной аппроксимации вольтамперной характеристики. R< h'°^!) max (d2/(x)), (10) где R – погрешность; h – шаг интегрирования; a и b – начальное и конечное значение оцениваемого отрезка времени интегрирования; f(x) – интегрируемая функция. В качестве иллюстраций на рис. 6 приведены расчетные осциллограммы токов (выделен красным цветом) и напряжений (выделен черным цветом) ВИГ КВ при номинальной нагрузке. На рис. 7 представлены осциллограммы, полученные в ходе экспериментального исследования ВИГ КВ на испытательном стенде в номинальном режиме. На рис. 8. Сопоставлен статический момент, полученный в результате расчета и экспериментально. Рис. 6. Расчетные осциллограммы токов и напряжений ВИГ КВ: а – ток и ЭДС якорной обмотки; б – ток и ЭДС дополнительной обмотки; в – ток и напряжение конденсатора возбуждения а) б) в) Рис. 7. Опытные осциллограммы токов и напряжений ВИГ КВ: а – ток и ЭДС якорной обмотки; б – ток и ЭДС дополнительной обмотки; в – ток и напряжение конденсатора возбуждения Анализируя полученные графики, можно отметить также следующие моменты. Ток якорной обмотки имеет постоянную составляющую. ЭДС обмотки возбуждения имеет значительные броски, обусловленные коммутацией, что усложняет выбор полупроводниковых компонентов. По конденсаторам возбуждения протекают значительные импульсные токи, что вызывает необходимость выбора более качественных компонентов с меньшим внутренним сопротивлением и индуктивно- стью. ЭДС якорной и дополнительной обмотки отличается в N раз, что обусловлено отношением количества витков. Заключение 1. Осуществлено математическое описание и разработана математическая модель ВИГ с принципиально новым способом возбуждения фазных обмоток, основанным на естественной коммутации конденсаторов за счет ЭДС нерабочей фазы. 2. Представленные результаты позволяют заключить, что разработанная математическая модель позволяет наглядно изучить электромагнитные процессы, имеющие место при работе ВИГ КВ. 3. Адекватность математической модели подтверждается тем, что расчетные токи и ЭДС достаточно близко совпадают с экспериментальными осциллограммами ВИГ КВ, полученными на испытательном стенде. 4. Разработанная математическая модель может стать основой как для отработки алгоритмов и выбора элементов схемы управления генератором, так и для создания упрощенной методики расчета параметров и его характеристик.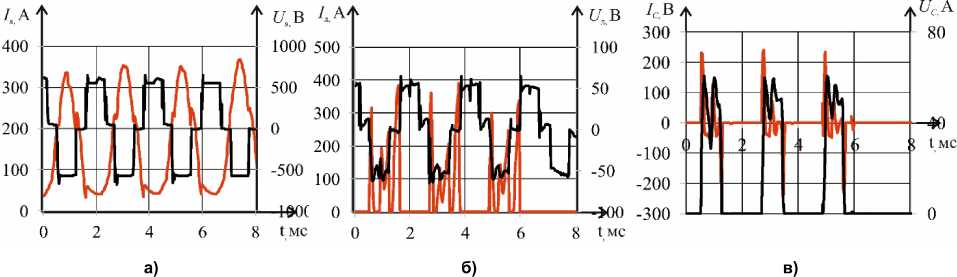
Список литературы Математическое описание вентильного индукторного генератора с конденсаторным возбуждением
- Коровин, В.А. Инновационная электромеханическая трансмиссия повышенной безопасности и экономичности /В.А. Коровин, А.Д. Чернышев // Вторая научно-практическая конференция «Разработка и использование электрических трансмиссий для образов вооружения и военной техники». - СПб., 2018.
- Гребенников, Н.В. Динамика и энергоэффективность перспективных единиц подвижного состава, оснащаемых вентильно-индукторными электрическими машинами: дис. ... канд. техн. наук /Н.В. Гребенников. - Ростов н/Д, 2012. - 148 с.
- Лашкевич, М.М. Разработка системы управления для электротрансмиссии с тяговыми вентильно-индукторными двигателями: дис. ... канд. техн. наук / М.М. Лашкевич. - М., 2013. -175 с.
- Туан, Н.М. Основные достоинства реактивно-вентильных электродвигателей по сравнению с традиционными электродвигателями / Н.М. Туан, Н.Ч. Хай // Известия Тульского государственного университета. Технические науки. -2014. -№ 8. - С. 184-187.
- Голландцев, Ю.А. Сравнение механических характеристик асинхронных и вентильных индукторно-реактивных двигателей // Информационно-управляющие системы. - 2006. -№ 6. - С. 50-53.
- Hrabovcova, V. Output Power of Switched Reluctance Generator with regard to the Phase Number and Number of Stator and Rotor Poles / V. Hrabovcova, P. Rafajdus, M. Liptak // Electronics and electrical engineering. - 2011. - No. 3. - P. 35-30.
- Song, Shoujuna. Detailed Design of a High Speed Switched Reluctance Starter/Generator for More/All Electric Aircraft / Song Shoujuna, Liu Weiguo, Dieter Peitsch // Chinese Journal of Aeronautics. - 2010. - No. 23. - P. 216-226. DOI: 10.1016/s1000-9361 (09) 60208-9
- Ganji, B. Modeling and analysis of switched reluctance generator using finite element method / B. Ganji, M. Heidarian, J. Faiz // Ain Shams Engineering Journal. - 2014. - No. 6. - P. 85-93. DOI: 10.1016/j.asej.2014.08.007
- Yuan-Chih, Chang. On the Design of Power Circuit and Control Scheme for Switched Reluctance Generator / Yuan-Chih Chang, Chang-Ming Liaw // IEEE transactions on power electronics. - 2008. -No. 1. - P. 445-454. DOI: 10.1109/tpel.2007.911872
- Grebennikov, N.V. Versions of Switched Reluctance Generator Design at a Constant Stator Configuration / N.V. Grebennikov, A.V. Kireev // International Journal of Power Electronics and Drive System. - 2015. - No. 1. - P. 65-69. DOI: 10.11591/ijpeds.v6.i1.pp65-69
- Najmeh, Faridnia. Voltage Control of a 12/8 Pole Switched Reluctance Generator Using Fuzzy Logic / Najmeh Faridnia, Masume Seyedyazdi, Faridoon Shabaninia // International Journal of Modern Nonlinear Theory and Application. - 2012. - No. 1. - P. 107-112. DOI: 10.4236/ijmnta.2012.13016
- Пат. 2658636 Российская Федерация. Индукторный генератор с совмещенными обмотками возбуждения и статора / В.А. Коровин; заявитель и патентообладатель Общество с ограниченной ответственностью Научно-производственное предприятие «Резонанс». - № 2017130438; заявл. 28.08.2017; опубл. 22.06.2018, Бюл. № 18.
- Заявка на патент Российской Федерации № 2019100979/07(001558). Индукторный генератор с совмещенными обмотками возбуждения и статора / В.А. Коровин, А.Д. Чернышев. -2019.
- Голландцев, Ю.А. Вентильные индукторно-реактивные двигатели прецизионных следящих систем электропривода: дис. . д-ра техн. наук / Ю.А. Голландцев. - СПб., 2004. - 299 с.
- Фисенко, В.Г. Проектирование вентильных индукторных двигателей / В.Г. Фисенко, А.Н. Попов. - М.: Изд-во МЭИ, 2005. - 56 с.
- Шевкунова, А.В. Совершенствование проектирования активной части вентильно-индукторной машины: дис. . канд. техн. наук: 05.09.01 / А.В. Шевкунова. - Екатеринбург, 2018. - 386 с.
- Голландцев, Ю.А. Вентильные индукторно-реактивные двигатели / Ю.А. Голландцев. -СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2003. -148 с.
- Лущик, В.Д. Вентильш генератори 1ндук-торного типу з сумщеними обмотками / В.Д. Лущик // В1сник Нацгонального техтчного унгверси-тету «Хартвський полгтехнгчний тститут». -2000. - № 84. - С. 129-130.
- Бакалов, В.П. Основы теории цепей: учеб. для вузов / В.П. Бакалов, В. Ф. Дмитриков, Б.И. Крук; под ред. В.П. Бакалова.- 3-е изд., перераб. и доп. -М.: Горячая линия - Телеком, 2007. - 597 с.
- Татур, Т.А. Основы теории электрических цепей: справ. пособие / Т.А. Татур. - М.: Высшая школа, 1980. - 271 с.
- Новожилов, О.П. Электроника и схемотехника: учеб. для СПО / О.П. Новожилов. - М.: Изд-во «Юрайт», 2018. - 282 с.
- Шишмарев, В.Ю. Электрорадиоизмере-ния: учебник для СПО / В.Ю Шишмарев. - М.: Изд-во «Юрайт», 2018. - 336 с.
- Чивилихин, С.А. Вычислительные методы в технологиях программирования. Элементы теории и практикум / С.А. Чвилихин. - СПб.: СПбГУ ИТМО, 2008. - 108 с.
- Фаустова, И.Л. Численные методы: учеб. пособие / И.Л. Фаустова. - Северск: Изд-во СТИ НИЯУ МИФИ, 2013. - 40 с.
- Огородникова, О.М. Вычислительные методы в компьютерном инжиниринге: учеб. пособие / О.М. Огородникова. - Екатеринбург: УрФУ, 2013. -130 с.


