Математика в художественном искусстве

Student

1st year, Institute of management Belgorod State National Research University Russia, Belgorod Maslakova L. F.

senior teacher of the Department of General Mathematics Belgorod State National Research University Russia, Belgorod

« Mathematics in art »

Многие ученые ставили целью своих работ доказать взаимосвязь математики и изобразительного искусства, появился даже такой научный термин как «математическое изобразительное искусство». Однако в данной статье речь пойдёт не об этом. Я не стану уподобляться известным научным деятелям, не стану стараться читателя в чём-то убедить, что-то изобрести или доказать, может, в чём-то наши мнения и сойдутся, но моя работа несёт исключительно анализирующий и поясняющий характер, путём практики.

Большинство людей считают, что способности к изобразительному искусству даются человеку от рождения, другими словами – это талант, но они даже не подозревают, что данным ремеслом можно овладеть путём изучения математической науки. Ведь любая деятельность – это, прежде всего, правильный, точный расчёт своих собственных действий и вычисление вероятности успешности своей работы.

Когда мы приходим в художественную школу, преподаватель изначальна, выясняет у нас каковы наши навыки, что мы умеем, прикидывает приблизительный объём работы. Уже по прошествии пары-тройки занятий мы начинаем привыкать к данной атмосфере, и тога педагог начинает раскрывать нам художественные тайны: с какого ракурса лучше смотреть, под каким углом держать карандаш, как точнее измерить размеры рисуемого предмета, как рассчитать правильный радиус, как выбрать начальную точку на холсте. Многие вышеперечисленные термины напрямую имеют связь с математикой, большая часть людей при знакомстве с техниками изобразительного искусства впадают в ступор, когда ты просишь их расставить набор объектов под тупым углом или рассчитать объём предложенной фигуры. Отсюда можно сделать первый вывод, чтобы овладеть художественным искусством, необходимо иметь хотя бы школьный курс знаний по точным наукам. Как писала в одной из своих работ учёный Злыгостева Татьяна Евгеньевна: «Проникнуть в тайны художественности им (А. Дюрера, Л. да Винчи, Р. Санти, В.И. Суриков) помогло знание методов точных наук, которые отыскали ряд математических законов, управляющих работой живописца в минуты, когда создается прекрасное».

Математика в живописи.

Значимость математики в различных художественных направлениях нельзя приуменьшать. Одним из ярких примеров того служит натюрморт, это один из жанров изобразительного искусства, на подобных картинах изображаются повседневные, обыденные вещи, неодушевлённые предметы, например, пища, посуда, книги, мебель и другое. Основой натюрморта служит композиция - это в первую очередь правильный выбор размера и расположения предмета в пределах заданного формата. При решении композиционных задач нельзя пренебрегать такими понятиями, как масштаб, пропорции, соразмерность, равновесие, тема, сюжет, образ, тон, форма, объем, конструкция, пространство (перспектива), симметрия, контраст, ритм, динамика, статика. Разве это не прямое доказательство взаимосвязи математики и композиционной живописи? В подтверждение того, приведу цитату художника-мариниста А. Жукова: «Отношения математики и живописи особенно близки, ибо эти виды деятельности зачастую используют один и тот же объект исследования. Более того, так же как математика может быть использована для анализа живописи, последняя в свою очередь (рисование, черчение, в частности) очевидно полезна в математических исследованиях, причем далеко не только в геометрии. Математику и живопись в этой связи можно рассматривать просто как два различных, взаимодополняющих способа визуализации конкретной или абстрактной реальности, в которой мы существуем».

Золотое сечение.

Наверняка, вы слышали о таком понятие как «золотое сечение», но мало, кто знает, что это. Данный термин используют в различных сферах: живопись, архитектура, музыка, математика, фотография. Но как же его вычислить? Прежде чем определить золотое сечение, необходимо ознакомиться с понятием пропорции. В математике пропорция - это равенство между двумя отношениями четырех величин: а : Ь = с : d. Для примера обратимся к отрезку прямой (рис. 1). Отрезок АВ можно разделить на две равные части (/). Это будет соотношение равных величин — АВ : АС = АВ : ВС. Эту же прямую (2, 3) можно разделить на две неравные части в любом отношении. Эти части пропорции не образуют. Отношение малого отрезка к большому или меньшего к большему есть, а соотношения (пропорции) нет. И, наконец, прямую АВ(4) можно разделить по золотому сечению, когда АВ : АС, как АС : ВС. Это и есть золотое деление или деление в крайнем и среднем отношении.

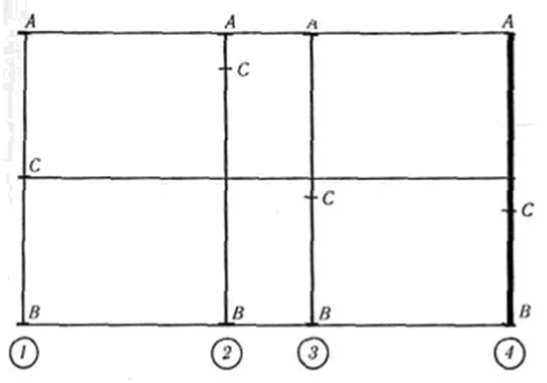
Рис. 1. Деление отрезка прямой на равные части и по золотому сечению: 1 — АВ:АС=АВ:ВС (образуется пропорция); 2, 3 — пропорция не образуется; 4—АВ:АС=АС:ВС или ВС:АС=АС:АВ (золотая пропорция)

Отсюда можно сделать вывод: золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, другими словами, меньший отрезок так относится к большему, как больший ко всему.

В данной статье я старалась обосновать свою точку зрения, что математика не просто связанна с художественным искусством, а является его неотъемлемой частью его. Вы можете согласиться, а можете и оспорить, в данном вопросе невозможно прийти к единому мнению.