Математико-статистический анализ данных по результатам морфофизиологического исследования ерша Лахтинской губы Онежского озера
Автор: Клюкина Елена Александровна, Дзюбук Ирина Михайловна
Журнал: Ученые записки Петрозаводского государственного университета @uchzap-petrsu
Рубрика: Физико-математические науки
Статья в выпуске: 6 (111), 2010 года.
Бесплатный доступ
Анализ данных, морфофизиологические параметры, ерш, онежское озеро, выборка, сравнение двух независимых выборок, компонентный анализ
Короткий адрес: https://sciup.org/14749772
IDR: 14749772
Текст статьи Математико-статистический анализ данных по результатам морфофизиологического исследования ерша Лахтинской губы Онежского озера
С 1999 года сотрудниками лаборатории экологических проблем Севера Петрозаводского государственного университета на базе Шелтозерской учебно-производственной станции проводятся ихтиологические исследования в рамках работ по мониторингу юго-западного района Онежского озера (Лахтинская губа), целью которых является изучение динамики состояния экосистемы, выявление возможностей использования и условий сохранения ее биоресурсов. В ходе исследований проводятся сбор и обработка материалов по различным видам рыб. В уловах в больших количествах встречается ерш, что дало возможность собрать репрезентативный материал.
Цель настоящего исследования – провести математико-статистический анализ данных по результатам морфофизиологического исследования ерша Лахтинской губы Онежского озера.
МАТЕРИАЛ И МЕТОДЫ ИССЛЕДОВАНИЯ
Отлов рыбы проводился в летний период (июль, 2002 год) с помощью ставных сетей. Были исследованы и проанализированы 94 особи возраста от 2+ до 8+, из них 75 самок и 19 самцов (табл. 1). Обработка ихтиологического материала осуществлялась по общепринятой методике [12].
При математико-статистической обработке результатов исследования применялся дескриптивный (описательный) анализ, методы сравнения двух независимых выборок и компонентный анализ. Оценка достоверности различий между средними арифметическими осуществлялась по критерию Стьюдента (t-тест), а между диспер- сиями - по критерию Фишера (F-тест) (при нормальном распределении признака). Нормальность распределения признака определяли по тесту Шапиро – Уилкса (W-тест). Оценка по t-, F- и W-тестам проводилась для уровня значимости α = 0,05. Все математические операции, графические построения и статистическая обработка данных проведены с использованием стандартных программных пакетов Word и Excel и компьютерной программы StatGraphics Centurion XV.
Таблица 1
|
Количество материала |
(n = |
94) |
||||||
|
Пол |
Возраст |
Всего |
||||||
|
2+ |
3+ |
4+ |
5+ |
6+ |
7+ |
8+ |
||
|
Самки |
4 |
16 |
22 |
15 |
6 |
6 |
6 |
75 |
|
Самцы |
3 |
4 |
9 |
3 |
0 |
0 |
0 |
19 |
|
Всего |
7 |
20 |
31 |
18 |
6 |
6 |
6 |
94 |
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Выборка состоит из самок и самцов. В данном случае мы имеем дело с альтернативным признаком (самка - самец). Таким образом, из 94 проб 75 содержат самок (значение 1), а 19 -не содержат (значение 0). Таким образом, выборка состоит из 75 единиц и 19 нулей. Доля вариант со значением 1 (доля самок) составляет:
p =
= 0,8
(то есть 80 %), тогда доля самцов составляет q = 0,2 (то есть 20 %). Отметим, что доля самок сильно отличается от доли самцов (в 4 раза), поэтому наиболее точные границы доверительного
интервала для альтернативного признака «пол ерша» даст φ-преобразование Фишера [7]. Итак, найдем границы доли самок ерша p = 0,8 при уровне значимости α = 0,05:
Флев. = 2,214 -1,96 ■ = 2,012, фправ..
= 2,214 + 1,96 ■ = 2,416, тогда 94
Р лев . (2,012) = 71,4%, Р прав . (2,416) = 87,4%.
То есть доля самок в генеральной совокупности (популяции ершей) составляет минимум 71,4 %, а максимум - 87,4 %.
Самки ерша были представлены возрастными группами от 2+ до 8+, самцы – от 2+ до 5+. Наибольшее количество особей как самок, так и самцов было возраста 4+ (пятилетки) (рис. 1). В отдельных возрастных группах соотношение полов было сдвинуто в сторону самок (рис. 2).
Размеры ерша были в пределах 20,4–82,0 г и 13,9–18,7 см (табл. 2), что значительно превышает размеры ерша из других районов Онежского озера. Например, размеры ерша Кондопожской губы (2+…7+) составляют 16,6–30,6 г и 11,7–14,3 см, а ерша района Кузаранды (1+…5+) – 7,9–14,6 г и 9,8–11,9 см [9]. Известно, что в большинстве карельских водоемов обитает мелкий ерш – 5–10 см и до 15 г, но в некоторых озерах он может достигать веса 50 и даже 100 г [5]. Ерш – медленнорастущий вид [6], [11]. Однако для ерша Лахтинской губы показатели роста (прирост длины, массы) значительны. Так, величины абсолютного прироста ерша Лахтинской губы находятся в диапазоне от 1,6 до 24,3 г и от 0,2 до 2,2 см. Максимальный абсолютный прирост массы и длины ерша характерен для возрастного периода 7+…8+ - 24,3 г, 2,2 см. Величина относительного прироста массы ерша наи- большая в возрасте 5+…6+ - 1,5 г, относительный прирост длины для всех возрастных периодов у ерша находится в пределах 1,0–1,1.
Потенциальные возможности роста ерша велики, и их реализация возможна в условиях хорошей обеспеченности пищей. Вероятно, что в условиях Лахтинской губы сложились благоприятные кормовые условия для ерша. Это подтверждают и результаты по упитанности ерша.
Таблица 2
Размерно-весовые показатели ерша Лахтинской губы (июль, 2002 год) (n = 94)
|
Параметры |
Возраст |
|||||||
|
2+ |
3+ |
4+ |
5+ |
6+ |
7+ |
8+ |
||
|
Масса, г |
♀♂ |
20,4 ± 3,8 |
29,1 ± 3,1 |
30,7 ± 1,4 |
35,6 ± 1,5 |
52,2 ± 2,4 |
57,7 ± 4,2 |
82,0 ± 6,0 |
|
♀ |
23,8 ± 6,2 |
28,7 ± 3,8 |
31,8 ± 1,7 |
36,6 ± 1,6 |
52,2 ± 2,4 |
57,2 ± 4,2 |
82,0 ± 6,0 |
|
|
♂ |
15,8 ± 2,2 |
30,5 ± 2,1 |
28,1 ± 2,2 |
30,3 ± 2,0 |
– |
– |
– |
|
|
Длина тела, см |
♀♂ |
13,9 ± 1,2 |
14,1 ± 0,5 |
14,3 ± 0,3 |
15,3 ± 0,3 |
16,0 ± 0,2 |
16,5 ± 1,0 |
18,7 ± 0,4 |
|
♀ |
13,4 ± 1,4 |
13,9 ± 0,7 |
14,6 ± 0,3 |
15,4 ± 0,3 |
16,0 ± 1,2 |
16,5 ± 1,0 |
18,7 ± 0,4 |
|
|
♂ |
14,6 ± 2,5 |
14,8 ± 0,2 |
13,5 ± 0,5 |
14,8 ± 0,6 |
– |
– |
– |
|
|
Упитанность |
♀♂ |
1,1 ± 0,2 |
1,3 ± 0,1 |
1,4 ± 0,1 |
1,2 ± 0,1 |
2,1 ± 0,7 |
1,9 ± 0,7 |
1,5 ± 0,1 |
|
♀ |
1,3 ± 0,1 |
1,3 ± 0,1 |
1,3 ± 0,1 |
1,3 ± 0,1 |
2,1 ± 0,7 |
1,9 ± 0,7 |
1,5 ± 0,1 |
|
|
♂ |
0,9 ± 0,4 |
1,3 ± 0,2 |
1,5 ± 0,1 |
1,1 ± 0,1 |
– |
– |
– |
|
Примечание. ♀♂ – общее, ♀ – самки, ♂ – самцы.
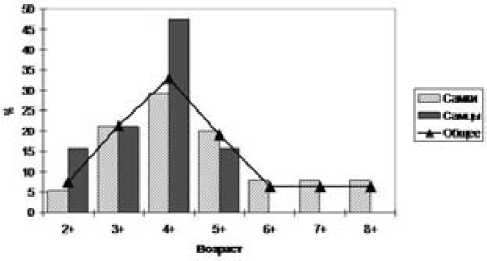
Рис. 1. Возрастной состав ерша Лахтинской губы Онежского озера (июль, 2002 год)
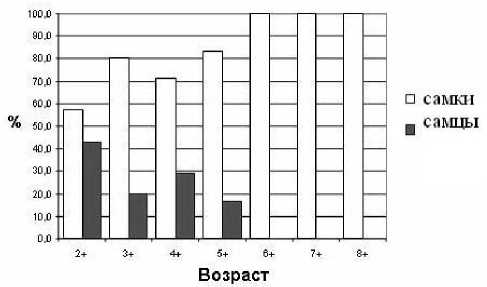
Рис. 2. Соотношение самок и самцов ерша Лахтинской губы Онежского озера (июль, 2002 год)
Упитанность (u) рассчитывали по следующей формуле:
100m u= , d3
где m - масса тела в г, d - длина тела без хвостового плавника в см. Величина u была в пределах 1,1–2,1, наиболее упитанными были рыбы (самки) возраста 6+…7+, наименее упитанными – возраста 2+ (табл. 2). В возрасте 2+ и старше ерш переходит от питания бентосом к хищничеству. Поэтому смена пищевых объектов, возможно, отражается на его упитанности.
В ходе анализа была проведена проверка нормального характера распределения ершей Лахтинской губы Онежского озера для уровня значимости α = 0,05 (для 94 особей) с помощью W-теста по следующим признакам: возраст, масса, длина тела, длина тела без хвостового плавника и упитанность. Результаты проверок представлены в табл. 3. Заметим, что только для длины тела (D) извлеченное из теста значение p > 0,05 (p = 0,150215), следовательно, гипотеза о нормальном распределении длины тела ершей Лахтинской губы принимается с надежностью, равной 95 %. Для остальных признаков с 5 % вероятностью ошибки гипотеза о нормальном распределении отвергается, причем для упитан- ности значение p настолько мало, что оно обозначено как 0,00.
На диаграммах нормального распределения (также называемых Quantile-Quantile Plot) видно, как близко заданное распределение приближается к нормальному (рис. 3). На диаграммах каждое наблюдаемое значение (ось ординат) сравнивается со значением, ожидаемым при нормальном распределении (ось абцисс). Также оценка соответствия данного распределения нормальному распределению представлена на гистограммах (рис. 4), тонкой линией показана кривая нормального распределения.
Таблица 3
Тесты на нормальное распределение
|
Тест |
Статистика |
p (P-Value) |
|
Шапиро – Уилкс (W-тест) |
Для возраста 0,88831 1 1,59334E-9 Для массы тела 0,899556 2,66951E-8 Для длины тела (D) 0,969756 1 0,150215 Для длины тела без хвоста (d) 0,960445 0,0306247 Для упитанности 0,649041 0,00 |
|
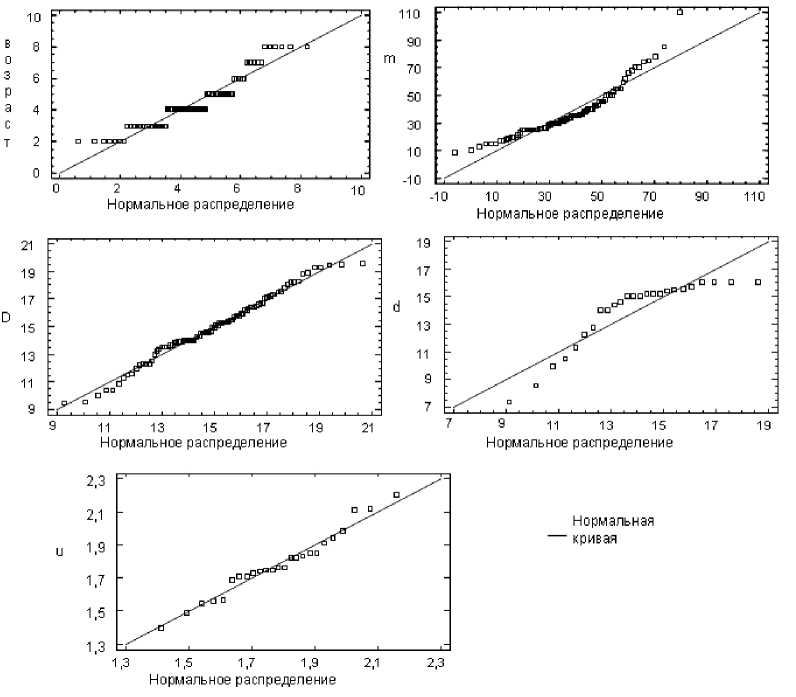
Рис. 3. Диаграммы нормального распределения для возраста, массы (m), длины тела D и d, упитанности (u) ерша
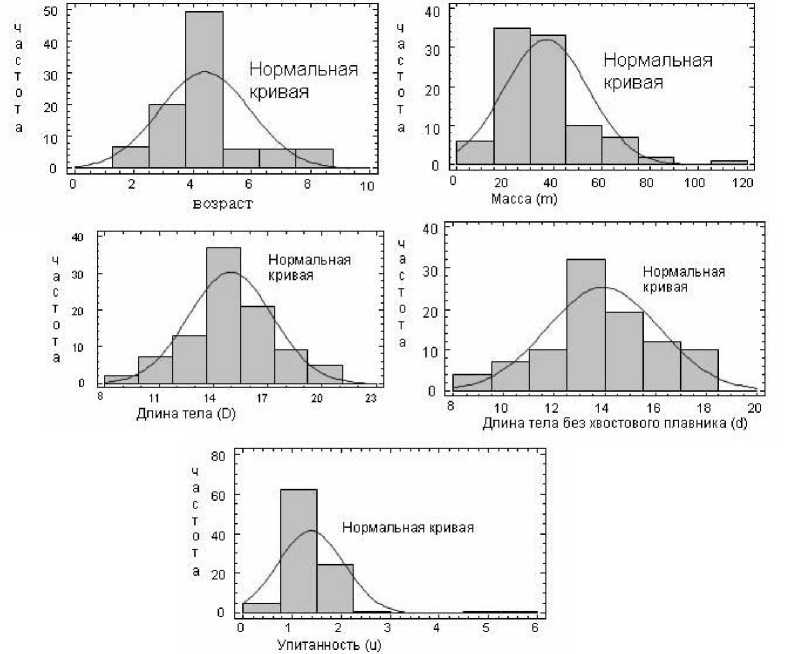
Рис. 4. Гистограммы соответствия нормальному распределению для возраста, массы (m), длины тела D и d, упитанности (u) ерша
Таблица 4
Общая статистическая характеристика для массы, длины тела
|
и упитанности ерша (2+…5+) |
||||||
|
Статистики |
Масса (m) |
Длина тела (D) |
Упитанность (u) |
|||
|
самки |
самцы |
самки |
самцы |
самки |
самцы |
|
|
Объем |
57 |
19 |
57 |
19 |
57 |
19 |
|
Среднее |
31,614 |
27,0263 |
14,5404 |
14,1684 |
1,26601 |
1,28563 |
|
Медиана |
32,0 |
26,0 |
14,5 |
14,3 |
1,2444 |
1,2289 |
|
Дисперсия |
117,884 |
50,9576 |
4,16102 |
3,63228 |
0,117528 |
0,213995 |
|
Стандартное отклонение |
10,8574 |
7,13846 |
2,03986 |
1,90585 |
0,342824 |
0,462596 |
|
Коэффициент вариации |
34,3437 % |
26,413 % |
14,0289 % |
13,4514 % |
27,0791 % |
35,982 % |
|
Минимальный предел варьирования |
9,0 |
12,5 |
9,5 |
9,6 |
0,4395 |
0,3662 |
|
Максимальный предел варьирования |
68,0 |
45,0 |
19,3 |
17,3 |
2,1478 |
2,3324 |
|
Размах выборки |
59,0 |
32,5 |
9,8 |
7,7 |
1,7083 |
1,9662 |
|
Стандартизированная асимметрия |
1,44497 |
0,545528 |
-0,481319 |
-1,14782 |
1,29383 |
0,670024 |
|
Стандартизированный эксцесс |
2,1101 |
1,65011 |
0,895464 |
0,63802 |
0,967495 |
0,929577 |
С помощью статистического пакета StatGraphics был проведен анализ отличий между самцами и самками ерша Лахтинской губы Онежского озера по различным признакам – массе, длине тела, упитанности, а также по индексам органов. Так как самцы возраста старше 5+ в выборке не представлены, для исследования отличий между самцами и самками ерша по этим признакам рассмотрена группа особей возраста 2+…5+ (всего 76 особей). В табл. 4 приведена общая статистика обеих выборок для массы (m), длины тела (D) и упитанности (u) ерша.
Подробнее результаты табл. 4 представлены на рис. 5 с помощью диаграмм частот встречаемости разных значений двух выборок и «ящиков с усами». «Ящики» (окрашенные прямоугольники) демонстрируют доверительные интервалы для средних, «усы» (тонкие линии) - размах варьирования данных, вертикальные линии, делящие каждый ящик на две части, - медианы, а крестиками обозначены средние выборок.
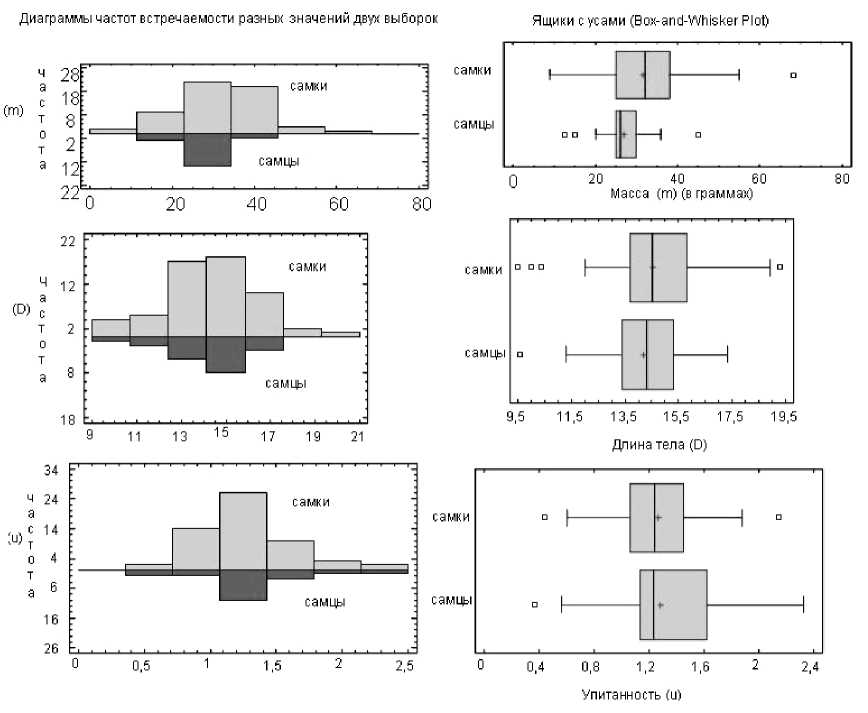
Рис. 5. Диаграммы частот встречаемости разных значений двух выборок и «ящики с усами» (для m, D, u)
Наибольший интерес из статистических характеристик в рамках данного анализа представляют стандартизированные эксцесс и асимметрия, с помощью которых можно определить, относятся ли эти выборки к нормально распределенным. Так, для самцов выборочные значения стандартизированных асимметрии и эксцесса массы тела попадают в нормальный диапазон, для самок стандартизированная асимметрия попадает в этот диапазон, а стандартизированный эксцесс немного (на 0,1101) превысил правую границу нормального диапазона. При этом доверительные интервалы на уровне надежности 95 % для выборочных средних по массе для самок и самцов соответственно равны [28,7332; 34,4949] и [23,5857; 30,467].
Проверка с помощью t-теста подтвердила гипотезу о равенстве среднего значения массы тела самок и самцов на уровне значимости α = 0,05: для альтернативной гипотезы о неравенстве средних вычисленное значение вероятности p = 0,0899609 > 0,05, то есть альтернативная гипотеза отвергается на уровне значимости α = 0,05. Доверительные интервалы на уровне надежности 95 % для стандартных отклонений для самок и самцов соответственно равны [8,23998; 12,0144] и [5,39391; 10,5565]. Отметим, что при- менение критерия Стьюдента предполагает равенство выборочных дисперсий.
Проверка равенства дисперсий с помощью критерия Фишера показала, что гипотеза о равенстве дисперсий выборок по массе тела не отвергается на уровне значимости α = 0,05 (p = 0,0519313 > 0,05). Это подтверждается также тем, что 95 % доверительный интервал для отношения различий [0,992631; 4,6309] содержит 1. Заметим, что для данного признака среди самок исследуемой возрастной группы 2+…5+ одна особь возраста 3+ значительно отличается (68 г при длине тела 17,1 см) от особей этого же возраста, для которых максимальный предел варьирования равен 55. Вероятно, возникла ошибка в определении возраста (возможно, при внесении данных в среду Excel). Исключив из рассмотрения данную особь (выброс), получим следующие значения стандартизированных асимметрии и эксцесса по массе: -0,338909 и -0,120373 соответственно, находящиеся в нормальном диапазоне.
Аналогично были проанализированы отличия между самцами и самками ерша по длине тела. Поскольку вычисленные значения стандартизированных асимметрии и эксцесса для обеих выборок находятся в пределах диапазона от -2 до 2 (табл. 4), нет оснований считать, что рас- пределение выборок по длине тела существенно отличается от нормального. Доверительные интервалы на уровне надежности 95 % для выборочных средних длины тела для самок и самцов соответственно равны [13,9991; 15,0816] и [13,2498; 15,087]. Проверка с помощью t-теста подтвердила гипотезу о равенстве среднего значения по длине тела самок и самцов на уровне значимости α = 0,05: для альтернативной гипотезы о неравенстве средних вычисленное значение вероятности p = 0,486634 > 0,05, то есть альтернативная гипотеза отвергается на уровне значимости α = 0,05.
Поскольку предположение о нормальном распределении выборок (длина тела самок и самцов) не отвергается, для проверки равенства дисперсий можно воспользоваться F-тестом. Доверительные интервалы на уровне надежности 95 % для стандартных отклонений по длине тела для самок и самцов соответственно равны [1,72216; 2,50239] и [1,44009; 2,81842]. Поскольку вычисленная вероятность p = 0,778036 > 0,05, гипотеза о равенстве дисперсий (то есть гипотеза о том, что рассмотренные выборочные дисперсии оценивают одну и ту же генеральную дисперсию) не отвергается на уровне значимости α = 0,05. На это же указывает доверительный интервал для отношения различий, который простирается от 0,491544 до 2,29319. Так как этот доверительный интервал содержит значение 1, нет статистически существенного различия между стандартными отклонениями этих выборок на уровне значимости α = 0,05.
Для упитанности вычисленные значения стандартизированных асимметрии и эксцесса для обеих выборок также находятся в пределах нормального диапазона от -2 до 2 (табл. 4). На уровне значимости α = 0,05 t-тест подтвердил гипотезу о равенстве среднего значения упитанности самок и самцов (p = 0,844168 > 0,05), а F-тест - гипотезу о равенстве дисперсий обеих выборок (p = 0,0908117 > 0,05).
В качестве морфофизиологических индикаторов состояния водной среды и организмов используют показатели массы органов рыб. Для анализа был проведен расчет индексов органов (в ‰), которые позволяют устранить существующую прямую пропорциональную зависимость массы органа от массы тела (табл. 5). Индекс органа (i) определяется по следующей формуле:
i=mo , m где mo - масса органа (в мг), m - масса тела (в г).
Для ерша Лахтинской губы характерны высокие показатели относительной массы сердца (2,7–3,9 ‰). Например, индексы сердца ерша (2+…7+) из Кондопожской губы Онежского озера составляют 1,8–2,0 ‰, ерша района Куза-ранды (1+…5+) – 1,9–2,2 ‰ [9]. Высокая относительная масса сердца, вероятно, является следствием того, что в имеющихся условиях среды Лахтинской губы у ерша высокие затраты энергии на обеспечение жизнедеятельности. В ходе исследований была подтверждена закономерность уменьшения индекса сердца ерша с возрастом.
Для анализа были исследованы отличия между самцами и самками ерша возрастной группы (2+…5+) по индексам сердца. В табл. 6 представлена общая статистика обеих выборок для самок и самцов ерша.
Индексы органов (‰) ерша Лахтинской
Таблица 5 губы Онежского озера (июль, 2002 год)
|
Органы |
Половой состав |
Возраст |
||||||
|
2+ |
3+ |
4+ |
5+ |
6+ |
7+ |
8+ |
||
|
Сердце |
♀♂ |
3,9 ± 0,6 |
3,6 ± 0,2 |
3,0 ± 0,1 |
3,0 ± 0,2 |
2,9 ± 0,2 |
2,8 ± 0,3 |
2,7 ± 0,3 |
|
♀ |
3,8 ± 1,1 |
3,7 ± 0,2 |
3,0 ± 0,1 |
3,1 ± 0,2 |
2,9 ± 0,2 |
2,8 ± 0,3 |
2,7 ± 0,3 |
|
|
♂ |
4,0 ± 0,2 |
3,2 ± 0,4 |
3,2 ± 0,2 |
2,7 ± 0,3 |
– |
– |
– |
|
|
Жабры |
♀♂ |
30,8 ± 5,3 |
31,8 ± 2,4 |
29,9 ± 1,6 |
31,2 ± 2,6 |
32,2 ± 2,7 |
28,5 ± 2,1 |
21,6 ± 4,6 |
|
♀ |
78,3 ± 21,4 |
104,3 ± 12,6 |
109,5 ± 7,7 |
31,6 ± 3,1 |
32,2 ± 1,7 |
28,5 ± 2,1 |
21,6 ± 4,6 |
|
|
♂ |
26,4 ± 1,3 |
26,1 ± 8,2 |
26,2 ± 3,1 |
29,4 ± 3,5 |
– |
– |
– |
|
|
Печень |
♀♂ |
15,0 ± 3,3 |
17,0 ± 1,7 |
16,5 ± 1,4 |
19,4 ± 2,0 |
19,2 ± 2,0 |
23,0 ± 1,9 |
20,0 ± 4,3 |
|
♀ |
42,4 ± 13,3 |
51,6 ± 9,9 |
60,8 ± 6,1 |
20,0 ± 2,4 |
19,2 ± 2,0 |
23,0 ± 1,9 |
20,0 ± 4,3 |
|
|
♂ |
10,2 ± 1,1 |
24,4 ± 5,5 |
14,3 ± 3,2 |
16,9 ± 0,4 |
– |
– |
– |
|
|
Селезенка |
♀♂ |
2,4 ± 0,6 |
2,6 ± 0,2 |
2,0 ± 0,1 |
2,0 ± 0,3 |
2,3 ± 0,8 |
1,4 ± 0,4 |
1,2 ± 0,3 |
|
♀ |
5,0 ± 1,3 |
7,9 ± 1,0 |
7,2 ± 0,7 |
1,8 ± 0,2 |
2,3 ± 0,8 |
1,4 ± 0,4 |
1,2 ± 0,3 |
|
|
♂ |
2,3 ± 1,2 |
2,4 ± 0,2 |
1,9 ± 0,1 |
2,9 ± 1,4 |
– |
– |
– |
|
|
Желудок |
♀♂ |
11,2 ± 1,8 |
10,2 ± 0,5 |
9,2 ± 0,7 |
10,3 ± 0,7 |
11,3 ± 1,4 |
7,8 ± 0,7 |
8,9 ± 1,3 |
|
♀ |
26,6 ± 6,1 |
31,0 ± 3,4 |
32,9 ± 2,0 |
10,9 ± 0,7 |
11,3 ± 1,4 |
7,8 ± 0,7 |
8,9 ± 1,3 |
|
|
♂ |
10,1 ± 1,8 |
10,0 ± 1,1 |
7,4 ± 1,0 |
7,2 ± 1,5 |
– |
– |
– |
|
|
Кишечник |
♀♂ |
12,3 ± 4,5 |
11,2 ± 0,9 |
10,8 ± 1,1 |
12,1 ± 1,5 |
9,9 ± 0,8 |
10,7 ± 1,6 |
10,7 ± 1,9 |
|
♀ |
29,1 ± 6,0 |
35,5 ± 4,7 |
37,0 ± 3,6 |
12,8 ± 1,7 |
9,9 ± 0,8 |
10,7 ± 1,6 |
10,7 ± 1,9 |
|
|
♂ |
7,4 ± 1,3 |
9,0 ± 0,7 |
9,7 ± 1,5 |
8,1 ± 1,2 |
– |
– |
– |
|
Отметим, что вычисленные значения стандартизированных асимметрии и эксцесса для самок ершей превышают правую границу диапазона от -2 до 2, что указывает на существенные отклонения от нормального распределения. Среди самок исследуемой возрастной группы 2+^5+ у одной самки возраста 2+ индекс сердца намного больше (6,58 %о), чем у других самок изучаемой группы (2+...5+), для которых максимальный предел варьирования равен 5,19. Это указывает на то, что либо у этой особи была патология сердца, либо она отличалась высокими энергетическими затратами для обеспечения жизнедеятельно сти.
Исключив из рассмотрения данную особь, мы получили следующие значения стандартизированных асимметрии и эксцесса для самок: 0,762207 и 0,653316 соответственно, которые, как и значения данных статистик для самцов, принадлежат нормальному диапазону. При этом для уровня значимости а = 0,05 проверка с помощью t-теста подтвердила гипотезу о равенстве среднего значения по индексу сердца самок и самцов (так как р = 0,40498 > 0,05); критерий Фишера показал, что гипотеза о равенстве дисперсий выборок также подтверждается на данном уровне значимости (p = 0,387831 > 0,05).
Индекс жабр ерша был в пределах 21,631,8 %о, что близко к величине относительной массы жабр ерша Кондопожской губы (30,234,8 ^) и Кузаранды (28,1-33,1 ^) [9]. Индексы жабр имеют прямую связь с изменением уровня газообмена, а интенсивность газообмена и потребность в кислороде зависят от характера пищи и активности рыб. Не выявлена зависимость изменений этого показателя от возраста рыб, однако у ерша в возрасте 8+ был наименьший индекс жабр по сравнению с рыбами младших возрастов.
Были исследованы отличия между самцами и самками ерша возрастной группы 2+^5+ по индексам жабр. Для обеих выборок значения стандартизированных асимметрии и эксцесса попадают в нормальный диапазон (табл. 6). При этом доверительные интервалы на уровне надежности 95 % для выборочных средних для самок и самцов соответственно равны [29,4207; 34,8688] и [22,1326; 31,2674]. Проверка с помощью t-теста не подтвердила гипотезу о равенстве среднего значения по индексу жабр самок и самцов на уровне значимости а = 0,05 (р = 0,0450151 < 0,05). Доверительные интервалы на уровне надежности 95 % для стандартных отклонений для самок и самцов соответственно равны [8,66739; 12,5942] и [7,16031; 14,0136]. Проверка равенства дисперсий с помощью критерия Фишера показала, что гипотеза о равенстве дисперсий выборок не отвергается на уровне значимости а = 0,05 (р = 0,731504 > 0,05), что подтверждается также тем, что 95 % доверительный интервал для отношения различий [0,503623; 2,34954] содержит 1.
Изменения массы печени за счет накопления или расходования углеводов и отчасти белков и жиров позволяют судить о характере метаболизма рыб. Так, индекс печени ерша Лахтинской губы колеблется в широком диапазоне: 15,023,0 %о. Для сравнения: индекс печени ерша Кондопожской губы составляет 21,7-26,8 %о, района Кузаранды - 11,8-14,2 %о [9]. Наименьший индекс печени был выявлен у ерша в возрасте 2+. С возраста 3+ происходит увеличение этого показателя, что, вероятно, связано со сменой пищевых объектов (переход к хищничеству) и с изменением метаболизма.
Таблица 6
Общая статистическая характеристика для индексов органов ерша (2 + ...5 + )
|
Статистики |
Индекс сердца |
Индекс жабр |
Индекс печени |
Индекс селезенки |
||||
|
самки |
самцы |
самки |
самцы |
самки |
самцы |
самки |
самцы |
|
|
Объем |
57 |
19 |
57 |
19 |
57 |
19 |
57 |
19 |
|
Среднее |
3,24614 |
3,26263 |
32,1447 |
26,7 |
17,5647 |
16,1663 |
2,18175 |
2,22789 |
|
Медиана |
3,2 |
3,4 |
32,35 |
28,0 |
17,59 |
14,0 |
2,1 |
2,0 |
|
Дисперсия |
0,934878 |
0,469532 |
105,397 |
89,7978 |
55,7116 |
84,3439 |
0,882325 |
1,30587 |
|
Стандартное отклонение |
0,966891 |
0,685224 |
10,2663 |
9,47617 |
7,46402 |
9,18389 |
0,939322 |
1,14275 |
|
Коэффициент вариации |
29,7859 % |
21,0022 % |
31,9378 % |
35,4913 % |
42,4944 % |
56,8088 % |
43,0535 % |
51,2927 % |
|
Минимальный предел варьирования |
1,37 |
2,04 |
10,0 |
3,46 |
3,2 |
5,19 |
0,53 |
0,02 |
|
Максимальный предел варьирования |
6,58 |
4,25 |
61,54 |
41,94 |
46,4 |
36,67 |
4,0 |
5,56 |
|
Размах выборки |
5,21 |
2,21 |
51,54 |
38,48 |
43,2 |
31,48 |
3,47 |
5,54 |
|
Стандартизированная асимметрия |
2,21536 |
-0,53324 |
1,62126 |
-1,55477 |
3,09413 |
2,08921 |
0,705979 |
2,13091 |
|
Стандартизированный эксцесс |
2,61973 |
-1,0336 |
1,98678 |
0,741828 |
4,36626 |
0,705396 |
-0,948447 |
3,2522 |
Также были проведены исследования отличий между самцами и самками ерша возрастной группы (2+…5+) по индексам печени. Выборочные значения стандартизированной асимметрии для самок и самцов, а также выборочное значение стандартизированного эксцесса находятся за пределами нормального диапазона, что указывает на существенные отклонения исследуемых выборок от нормального распределения (табл. 6). Однако среди самок исследуемой возрастной группы 2+…5+ индекс печени у одной самки возраста 5+ (46,4 ‰) намного больше, чем у остальных самок этой выборки. Среди самцов исследуемой возрастной группы 2+…5+ у самца возраста 4+ и у самца возраста 3+ индекс печени (36,67 и 35,48 ‰ соответственно) намного больше, чем у других самцов изучаемой группы, для которых максимальный предел варьирования равен 30,56. Это указывает на то, что у данных особей могла быть патология печени .
Исключив из рассмотрения эти особи, мы получили следующие значения стандартизированных асимметрии и эксцесса для индекса печени: 0,455248 и -0,377295 для самок, 1,67233 и 1,62625 для самцов, которые принадлежат нормальному диапазону. При этом для уровня значимости α = 0,05 проверка с помощью t-теста подтвердила гипотезу о равенстве среднего значения индекса печени самок и самцов (так как p = 0,0728045 > 0,05), а критерий Фишера показал, что гипотеза о равенстве дисперсий выборок также подтверждается на данном уровне значимости (p = 0,968315 > 0,05).
Известно, что масса селезенки по сравнению с массой других органов варьирует в бóльших пределах. Это связано с ее разнообразной функциональной деятельностью: продуцирование форменных элементов крови (эритроциты и лейкоциты), депонирование крови, образование лимфоцитов. Индекс селезенки ерша Лахтин-ской губы был в пределах 1,2–2,6 ‰. Для ерша Кондопожской губы и Кузаранды этот показатель находится в диапазоне 1,0–1,3 ‰ и 1,4– 1,5 ‰ соответственно. Вероятно, в условиях Лахтинской губы интенсивность работы селезенки у ерша очень высока. Наибольшие показатели отмечены у рыб возраста 3+ (2,6 ‰), что может быть связано с перестройкой пищевой активности и метаболизма в этом возрасте.
Исследованы отличия между самцами и самками ерша возрастной группы 2+…5+ по индексам селезенки. Отметим, что выборочные значения стандартизированных асимметрии и эксцесса для самцов, в отличие от самок, находятся за пределами нормального диапазона, что указывает на существенные отклонения данной выборки от нормального распределения (табл. 6). Однако заметим, что среди самцов исследуемой возрастной группы 2+…5+ у одного самца возраста 5+ индекс селезенки (5,56 ‰) намного больше, чем у других самцов изучаемой группы (2+…5+), для которых максимальный предел варьирования равен 3,93. Это объясняется патологией или тем, что у этих особей интенсивность работы селезенки в силу каких-то причин была больше, чем у других.
Исключив из рассмотрения данную особь, мы получили следующие значения стандартизированных асимметрии и эксцесса для индекса селезенки самцов: -0,309174 и 1,69731, которые принадлежат нормальному диапазону. При этом для уровня значимости α = 0,05 проверка с помощью t-теста подтвердила гипотезу о равенстве среднего значения по индексу селезенки самок и самцов (так как p = 0,576234 > 0,05), а критерий Фишера показал, что гипотеза о равенстве дисперсий выборок также подтверждается на данном уровне значимости (p = 0,597917 > 0,05).
Весовые показатели пищеварительного тракта (индексы желудка и кишечника) могут быть использованы в качестве характеристики обмена веществ в организме рыб, так как пищеварительный тракт перерабатывает разные пищевые компоненты, которые могут иметь разную пищевую ценность и разную степень усвояемости. Поэтому нагрузка на него может существенно колебаться, что способствует изменению его весовых параметров [13], [14].
Исследованы отличия между самцами и самками ерша возрастной группы 2+…5+ по индексам желудка. Общая статистика обеих выборок для самок и самцов ерша представлена в табл. 7.
В отличие от самцов, выборочные значения стандартизированных асимметрии и эксцесса для индекса желудка самок находятся за пределами нормального диапазона, что указывает на существенные отклонения данной выборки от нормального распределения. Однако среди самок исследуемой возрастной группы у самки возраста 2+ и особей возраста 4+ индексы желудка (19,78 и 22,50 ‰ соответственно) гораздо больше, чем у других самок изучаемой группы, для которых максимальный предел варьирования равен 17,65.
Таблица 7
Общая статистическая характеристика для индексов желудка и кишечника ерша (2+…5+)
|
Статистики |
Индекс желудка |
Индекс кишечника |
||
|
самки |
самцы |
самки |
самцы |
|
|
Объем |
57 |
19 |
57 |
19 |
|
Среднее |
10,4218 |
8,33316 |
12,1174 |
8,94211 |
|
Медиана |
10,0 |
8,23 |
10,6 |
9,14 |
|
Дисперсия |
12,4935 |
8,12126 |
44,7042 |
10,9703 |
|
Стандартное отклонение |
3,53462 |
2,84978 |
6,68612 |
3,31214 |
|
Коэффициент вариации |
33,9158 % |
34,1981 % |
55,178 % |
37,0398 % |
|
Минимальный предел варьирования |
4,67 |
2,89 |
3,71 |
4,27 |
|
Максимальный предел варьирования |
22,5 |
13,53 |
38,89 |
18,0 |
|
Размах выборки |
17,83 |
10,64 |
35,18 |
13,73 |
|
Стандартизированная асимметрия |
3,31705 |
0,161026 |
5,99432 |
1,85111 |
|
Стандартизированный эксцесс |
2,83249 |
-0,229915 |
7,10964 |
1,51976 |
Исключив из рассмотрения данные особи, мы получили следующие значения стандартизированных асимметрии и эксцесса для индекса желудка самок: 1,23733 и -0,117339, которые принадлежат нормальному диапазону. При этом для уровня значимости α = 0,05 проверка с помощью t-теста гипотезы о равенстве среднего значения по индексу желудка самок и самцов также не подтвердилась (p = 0,0307113 < 0,05). Критерий Фишера показал, что гипотеза о равенстве дисперсий выборок подтверждается на данном уровне значимости (p = 0,963301 > 0,05).
Результаты исследования отличия между самцами и самками ерша возрастной группы 2+…5+ по индексам кишечника показали, что для самцов выборочные значения стандартизированных асимметрии и эксцесса для индекса кишечника принадлежат нормальному диапазону от -2 до 2 (табл. 7). Для самок значения данных статистик превышают правый предел нормального диапазона более чем в 2,98 и 3,55 раза соответственно, что указывает на существенные отклонения данной выборки от нормального распределения. Таким образом, по индексу кишечника самки и самцы имеют существенные различия, поскольку не являются однородными (заданы разными законами распределения).
Также в рамках данного исследования была решена задача оценки степени различия между самками (57 особей) и самцами (19 особей) половозрелых ершей Лахтинской губы, возраст которых варьируется от 2+ до 5+, по следующим 9 морфологическим признакам: массе тела (m), длине D и d, индексам сердца, печени, селезенки, желудка, кишечника, жабр. Даная задача решалась с помощью компонентного анализа в среде статистического пакета StatGraphics.
Отметим, что компонентный анализ (метод главных компонент) как один из многомерных методов является отражением двух основных тенденций развития современной биометрии. С одной стороны, это стремление к более полному (многоплановому, многомерному) изучению действительности, что требует количественной оценки большого числа свойств исследуемых объектов. С другой стороны, это формирование все более наглядного, интегрированного, обобщенного представления об огромных массивах информации [7]. Наблюдения за эколого-биологическими феноменами дают n объектов (в нашем случае особей ерша), охарактеризованных набором из s признаков (в нашем случае это масса тела, длина тела, длина тела без хвостового плавника, масса органов и др.).
Компонентный анализ стремится сконцентрировать информацию об отличиях объектов в гораздо меньшее число расчетных индексов (k < s), называемых главными компонентами. Новые показатели отображают в себе общие причины, в силу которых группы признаков изменяются параллельно, а группы объектов оказываются сходными. В качестве таких общих факторов, например, мо- гут выступать пол, возраст, состояние здоровья. Значение каждого признака xj (j = 1, $) особи распадается на несколько частей, каждая из которых связана с действием определенной причины (a, b, c ...): Xj = xj + xbj + xj + ... Тогда сумма вкладов, например фактора a , в значения всех s признаков вычисляется по формуле: ГКа = xa 1 + xa 2 + ••• + xa$, гДе xaj (j = 1, $) -вклад фактора a в значение варианты j-го признака. Выразим эффект действия фактора a на j-й признак как долю от общего значения варианты следующим образом: xaj = aj • xj, где aj - относительный вклад данного фактора в конечное значение варианты, xj - значение варианты j-го признака. Тогда уравнение первой главной компоненты имеет вид: FKa = a1 • x1 + a2 • x2 +. „ + a$ • x$. Аналогично определяются уравнения второй главной компоненты ГКb и всех последующих. Коэффициенты (aj и т. п.), стоящие перед значениями признаков Xj (j = 1, $) в уравнениях компонент, являются аналогами коэффициентов корреляции данных признаков с общим фактором и называются факторными нагрузками [8]. Низкое значение факторной нагрузки говорит о независимости признака от данного фактора. Компонентный анализ эффективно «концентрирует» информацию: дисперсии первых компонент выражают большую долю общей изменчивости. Так, первые 2-3 компоненты накапливают в себе основную содержательную информацию об отличиях объектов, заменяя собой s исходных признаков.
Применение общего фактора «пол особи» позволило дать оценку степени различия между самками и самцами половозрелых ершей Лах-тинской губы (2+…5+) по описанным выше 9 морфологическим признакам (то есть число признаков s = 9). Результаты расчетов представлены в табл. 8 (в расчетах используются нормированные значения исходных признаков).
Таблица 8
Результаты расчетов компонентного анализа для общего фактора «пол особи»
|
Номер компоненты |
Значение дисперсий главных компонент (Eigenvalue) |
Относительный вес главных компонент (Percent of variance) |
Суммативный вес главных компонент (Cumulative percentage) |
|
1 |
3,37857 |
37,540 |
37,540 |
|
2 |
2,09512 |
23,279 |
60,819 |
|
3 |
1,26672 |
14,075 |
74,893 |
|
4 |
0,719251 |
7,992 |
82,885 |
|
5 |
0,53556 |
5,951 |
88,836 |
|
6 |
0,454349 |
5,048 |
93,884 |
|
7 |
0,289387 |
3,215 |
97,100 |
|
8 |
0,237479 |
2,639 |
99,738 |
|
9 |
0,0235633 |
0,262 |
100,000 |
Заметим, что первая компонента учла в себе большую долю исходной изменчивости (ее дисперсия S ГК К 1 = 3,37857 из 9, относительный вес составляет 37,54 %). Информативность второй компоненты выражается дисперсией S ГКК 2 = 2,09512 и относительным весом, равным 23,279 %. Информативность третьей компоненты выражается дисперсией S ГК к 3 = 1,09512 и относительным весом, равным 14,075 %. Дисперсии остальных компонент меньше единицы, что указывает на их низкую информативность, поскольку по умолчанию минимальное значение дисперсии главной компоненты (Minimum Eigenvalue) принимается равным 1. График Scree Plot отражает изменение дисперсий компонент (сплошная линия) и минимальный уровень компонент (пунктир) (рис. 6).
Значения факторных нагрузок для первых трех главных компонент рассматриваемых морфологических признаков представлены в табл. 9.
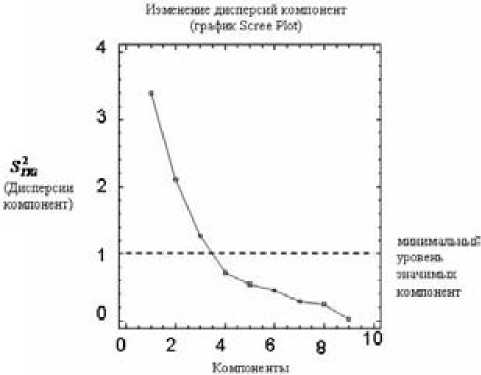
Рис. 6. Изменение дисперсий компонент для общего фактора «пол особи»
Таблица 9
Таблица значений факторных нагрузок в главных компонентах
|
Признаки |
Компонента 1 |
Компонента 2 |
Компонента 3 |
|
Масса тела (m) (г) |
0,412956 |
0,223743 |
-0,0206958 |
|
Длина тела (D) (см) |
0,402107 |
0,370433 |
-0,233382 |
|
Длина тела без хвостового плавника (d) (см) |
0,415668 |
0,359758 |
-0,204312 |
|
Индекс сердца (m1) (мг) |
-0,394719 |
0,0904513 |
-0,460582 |
|
Индекс печени (m2) (мг) |
-0,01825 |
0,494377 |
0,270413 |
|
Индекс селезенки (m3) (мг) |
-0,31011 |
0,117718 |
-0,550079 |
|
Индекс желудка (m4) (мг) |
-0,315346 |
0,393559 |
0,279557 |
|
Индекс кишечника (m5) (мг) |
-0,30411 |
0,306402 |
0,419827 |
|
Индекс жабр (m7) (мг) |
-0,225314 |
0,409968 |
-0,2472 |
Уравнение расчета значений первой компоненты следующее:
Component 1 = 0,413 • m + 0,402 • D + 0,416 • d -- 0,395 • m 1 - 0,018 • m 2 + 0,31 • m 3 -- 0,315 • m 4 - 0,304 • m 5 - 0,225 • m 6.
Все факторные нагрузки первых трех признаков положительны и больше 0,3, остальные отрицательны, причем для индексов печени и жабр факторные нагрузки по модулю меньше 0,3, то есть их влияние наименее значимо. Первую компоненту можно назвать «Уменьшение индексов сердца, селезенки, желудка и кишечника при увеличении массы и размеров ерша». Для второй компоненты все факторные нагрузки положительны, причем для массы тела и индексов сердца и селезенки их величина меньше 0,3. Поэтому вторую компоненту можно назвать «Увеличение индексов печени, жабр, желудка и кишечника при увеличении размеров тела». Третью компоненту можно назвать «Уменьшение индекса селезенки и индекса сердца при увеличении индекса кишечника», поскольку она объясняется в основном за счет переменных «индекс селезенки», «индекс сердца» и «индекс кишечника», их факторные нагрузки равны 0,55, -0,461 и 0,42 соответственно.
Рассмотрим численные характеристики особей, выраженные в трех главных компонентах (табл. 10). Для всех главных компонент и самцов (f), и самок (с) эти значения принимают как положительные, так и отрицательные значения, то есть для этих компонент знак численной характеристики особи не зависит от пола.
ЗАКЛЮЧЕНИЕ
В условиях Лахтинской губы Онежского озера ерш имеет максимальные размеры, высокие приросты и упитанность, а также максимальные индексы сердца и пищеварительного тракта, широкий диапазон колебаний индекса селезенки и печени по сравнению с этими показателями у ерша в других районах Онежского озера (Кондопожская губа, Кузаранда). С большой вероятностью можно считать, что в 2002 году в Лахтин-ской губе сложились наиболее благоприятные пищевые условия для ерша, что, возможно, связано с работой форелевого хозяйства. По результатам отлова и опросным данным известно, что в период функционирования хозяйства в губе качественный и количественный состав рыб в уловах был высоким. Появился лещ, не встречавшийся в этом районе до организации хозяйства. В больших количествах стали вылавливать ряпушку, плотву и другие виды. Известно, что при переходе к хищничеству ерш часто охотится на рыбу, включая молодь того же вида. Он охотно поедает икру различных видов рыб (ряпушки, леща, плотвы). Сложившиеся в Лахтинской губе благоприятные кормовые условия для ерша, обусловленные работой хозяйства, отразились на его морфофизиологическом состоянии.
Для ершей возрастной группы 2+…8+ с 95 % достоверной вероятностью было выявлено, что длина его тела имеет нормальное распределение.
С 95 % достоверностью выявлено отличие самок и самцов одной возрастной группы 2+…5+ по весовым показателям пищеварительного тракта (индексам желудка и кишечника) и по индексу жабр. Для остальных морфофизиологических признаков (масса, длина тела, длина тела без хвостового плавника, упитанность, индексы сердца, печени, селезенки), за исключением особей с патоло- гией, существенных различий между самками и самцами на уровне значимости 5 % не обнаружено (при нормальном характере распределения выборок). Также для ершей возрастной группы 2+…5+ были замечены следующие закономерности: 1) уменьшение индексов сердца, селезенки, желудка и кишечника при увеличении массы и размеров ерша; 2) увеличение индексов печени, жабр, желудка и кишечника при увеличении размеров тела; 3) уменьшение индексов селезенки и сердца при увеличении индекса кишечника, которые не зависят от пола рыбы (ерша Лахтинской губы Онежского озера).
Таблица 10
|
Численные характеристики особей, выраженные в главных компонентах |
|||||||||
|
№ ряда |
Метка (c – самка, f – самец) |
Компонента 1 |
Компонента 2 |
Компонента 3 |
№ ряда |
Метка (c – самка, f – самец) |
Компонента 1 |
Компонента 2 |
Компонента 3 |
|
1 |
c |
-6,12308 |
1,41647 |
2,3042 |
39 |
c |
1,6869 |
-0,521527 |
0,801433 |
|
2 |
c |
-4,45018 |
1,58058 |
-2,11261 |
40 |
c |
1,65057 |
1,70079 |
2,3146 |
|
3 |
c |
2,28985 |
-2,10592 |
-0,454106 |
41 |
c |
2,07744 |
1,81038 |
-1,71901 |
|
4 |
c |
1,84703 |
-0,125954 |
1,44667 |
42 |
c |
0,589043 |
-1,37391 |
-0,317117 |
|
5 |
f |
-2,0432 |
-3,30558 |
1,5707 |
43 |
c |
1,34662 |
-1,86487 |
0,0435226 |
|
6 |
f |
-0,258481 |
0,599828 |
-1,92146 |
44 |
c |
1,45519 |
0,251025 |
0,0562624 |
|
7 |
f |
0,384944 |
-0,276337 |
-2,14482 |
45 |
c |
1,11879 |
-0,832046 |
-1,07978 |
|
8 |
c |
-4,33018 |
-1,00817 |
0,481406 |
46 |
c |
0,960517 |
0,0433192 |
-0,975247 |
|
9 |
c |
-2,27951 |
-3,06538 |
0,0450712 |
47 |
c |
2,00865 |
0,898473 |
-1,25265 |
|
10 |
c |
-2,76973 |
-1,88369 |
0,178356 |
48 |
c |
0,111796 |
0,696392 |
-0,491625 |
|
11 |
c |
-1,10599 |
-1,38561 |
0,579863 |
49 |
c |
3,09015 |
-0,753296 |
-0,0735608 |
|
12 |
c |
0,1922 |
0,130438 |
-1,96484 |
50 |
f |
-0,557063 |
-3,05861 |
-0,315866 |
|
13 |
c |
-0,876327 |
-1,71357 |
0,0678525 |
51 |
f |
-0,347011 |
-1,09079 |
-1,01857 |
|
14 |
c |
-0,433809 |
0,34987 |
-0,604301 |
52 |
f |
-1,26734 |
0,294449 |
0,582169 |
|
15 |
c |
-0,211629 |
0,831523 |
0,681087 |
53 |
f |
-0,489403 |
-0,864343 |
0,571373 |
|
16 |
c |
-1,97457 |
0,864856 |
-1,72525 |
54 |
f |
-0,625915 |
-0,796724 |
-0,453623 |
|
17 |
c |
-3,58448 |
1,11715 |
-1,20036 |
55 |
f |
0,399526 |
-0,376344 |
0,226167 |
|
18 |
c |
0,808437 |
1,00611 |
-0,949569 |
56 |
f |
0,0658157 |
-3,55223 |
0,366113 |
|
19 |
c |
-0,117693 |
-0,328563 |
-0,115229 |
57 |
f |
-0,157844 |
1,25817 |
0,675066 |
|
20 |
c |
-1,59095 |
1,14218 |
-0,0949976 |
58 |
f |
3,19381 |
-2,34388 |
0,0729681 |
|
21 |
c |
0,29709 |
-0,737892 |
-1,10293 |
59 |
c |
-0,196112 |
-0,504879 |
0,799256 |
|
22 |
c |
2,75963 |
2,47286 |
-1,58159 |
60 |
c |
0,0431036 |
-0,994454 |
-0,359415 |
|
23 |
c |
4,49462 |
0,704298 |
0,53886 |
61 |
c |
0,559504 |
0,361771 |
-0,124298 |
|
24 |
f |
1,04563 |
-0,828179 |
0,707224 |
62 |
c |
1,04332 |
1,36969 |
-1,14579 |
|
25 |
f |
-0,722265 |
-0,00961921 |
-0,736094 |
63 |
c |
0,315808 |
2,05829 |
1,38357 |
|
26 |
f |
-0,669869 |
1,26956 |
-0,273727 |
64 |
c |
-0,182978 |
0,571661 |
0,454876 |
|
27 |
f |
1,35892 |
0,560471 |
0,66861 |
65 |
c |
0,779205 |
0,444373 |
0,138653 |
|
28 |
c |
-1,99887 |
-0,469097 |
2,18703 |
66 |
c |
2,02667 |
-0,153904 |
1,40277 |
|
29 |
c |
-3,26901 |
2,36922 |
1,35051 |
67 |
c |
0,441921 |
1,6244 |
-0,497019 |
|
30 |
c |
-1,00794 |
0,33046 |
0,290611 |
68 |
c |
-2,84282 |
1,94485 |
-1,91719 |
|
31 |
c |
-1,23955 |
-1,18104 |
0,101608 |
69 |
c |
0,42474 |
1,25727 |
2,85178 |
|
32 |
c |
-1,79385 |
1,78507 |
-0,755595 |
70 |
c |
2,0433 |
0,064037 |
0,44329 |
|
33 |
c |
-0,0532005 |
-0,959125 |
0,337348 |
71 |
c |
0,913886 |
-0,685667 |
-0,645632 |
|
34 |
c |
-0,213046 |
-0,577952 |
0,222258 |
72 |
c |
2,41815 |
-0,0865143 |
0,359717 |
|
35 |
c |
0,266583 |
-0,841282 |
1,52479 |
73 |
c |
1,97936 |
4,88588 |
1,99735 |
|
36 |
c |
-0,761346 |
1,38452 |
1,22434 |
74 |
f |
-0,578833 |
-0,783703 |
-2,26556 |
|
37 |
c |
0,199767 |
0,890789 |
-0,611525 |
75 |
f |
0,606633 |
0,0867251 |
0,534439 |
|
38 |
c |
0,0990222 |
-0,559134 |
0,512173 |
76 |
f |
1,72993 |
-0,428431 |
-0,094992 |
Список литературы Математико-статистический анализ данных по результатам морфофизиологического исследования ерша Лахтинской губы Онежского озера
- Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Основы моделирования и первичная обработка данных: Справочное издание. М.: Финансы и статистика, 1983. 471 с.
- Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 с.
- Боровиков В. П., Боровиков И. Д. Statistica. Статистический анализ и обработка данных в среде Windows. М.: Информационно-издательский дом «Филин», 1997. 608 с.
- Гублер Е. В., Генкин А. А. Применение непараметрических критериев статистики в медико-биологических исследованиях. Л.: Медицина, 1973. 142 с.
- Ивантер Д. Э., Рыжков Л. П. Рыбы. Петрозаводск: Изд-во ПетрГУ, 2004. 176 с.
- Ковалев П. М. Биологические особенности окуня и ерша озер Ильмень и Псковско-Чудского//Сб. науч. тр. ГосНИОРХ. Вып. № 236. Л., 1985. С. 117-127.
- Коросов А. В. Специальные методы биометрии: Учеб. пособие. Петрозаводск: Изд-во ПетрГУ, 2007. 364 с.
- Коросов А. В., Горбач В. В. Компьютерная обработка биологических данных: Метод. пособие. Петрозаводск: Изд-во ПетрГУ, 2010. 84 с.
- Крупень И. М. Морфофизиологические особенности ерша Gymnocephalus cernuus L. из различных условий обитания: Дис. … канд. биол. наук. Петрозаводск, 1999. 190 с.
- Малета Ю. С., Тарасов В. В. Непараметрические методы статистического анализа в биологии и медици-не. М.: Изд-во МГУ, 1982. 178 с.
- Мельянцев В. Г. Рыбы. Петрозаводск: Карелия, 1974. 120 с.
- Правдин И. Ф. Руководство по изучению рыб. М.: Пищ. пром-сть, 1966. 376 с.
- Смирнов В. С., Божко А. М., Рыжков Л. П., Добринская Л. А. Применение метода морфофизиологических индикаторов в экологии рыб//Тр. Т. 7. Петрозаводск, 1972. 190 с.
- Строганов Н. С. Экологическая физиология рыб. М.: Изд-во АН СССР, 1962. 444 с.


