Mathematical model of conducting nanopore for molecular dynamics simulations

Introduction. Nanopores represent a Sype о pores wi/C a diameter of about vrvcrel nanametars. Channels of such sisce canbcbslthnrllacllclldaltiflaialla madeobjects. Currently rcscai'cliott leka areai inleresi in tire Sssuas of studyingand modeling ofnanopokepropertfeseuf te their broaC epplicotean in science and technology [1)2]. Artificial nokpyoret nan lee usod, for охрипл fan imttoOan of Oiologicaf nanopase innoiions. TCey alre Cavr sttractive poteoUrlappIicaOc>nl in natloflшdficlds [35. Amongidese application" are stesolinotion, ionic sieves [4], scnotess Пог btotogiccl eoents dhd sequencing of DNNor 4CNA [5].

Vaoioui forms ot аппИаа. ponapoues usinp different produntion Scchnoioaics and maeerialu, inahlding polymers, inorganic euOrianeeb, biotic tom c6; k].

Conducting nanopasas attract fonslavrab«c aOentton due to tdiev importank polentiat ppplicotinns. tn u noarber oi works produ^tiae mcihohs of eimnlai" sSeovSures are gioen. For rxrmdle" cuch nekoporee ran Ise mane via integration «el⁷ enrison steueОtoes into Oho cocresponding nanoporous rtcteri^l. A mulllleyvecd cacOon nanotube was made incata a pore anU ah iOu sur"⁷oce of an anode aluminum oxICn mernbrane, acgtylna doc method of cdfmlaal xtmCnentotion from a steam pease t8(. Sttength-ened single-layer metal coition nanutubes wooe ckown on a sliicon plata vie fhemlcai sedimfnSatton fram a steam phase [9b aontdesis oO conduetinr eckt)on tubules inside the pores oi tie ekdda alшcOnvm and axiaic orrmlerane was OesestigaCed [10). Slmiiar etruceoree con be «nd interest in terms of yroCuftion ol selective rovmboanes switched by 1С:сСпс1Хс>Ь.

hi reetanl years metnrmatiroX ond clccttcmycl models oi ion transport in various lanco fa nanopnces fnd nano-cnondeis leave been viuorousee PeaetoneP, computer modeling of poeeeesea Oeve C>ern earned oul as well [11:13^

At fom|rueer modding oi nan ttanoport, applying methods ni molecelac «lynemics, the ргоЫет oC electric field dnlhtmg, created tn She system, hit to ho eolacd at each rted tn time. In poesence eV eleoiro-eondue-ive elements de iCh systemo eoMng sunh u talk with eiclsical methods r>cfvpi>s rathen rfeourcclmtcns>\т« Tkvrefore, problem tolvina metiloУs oC ecvk rtectrootatic tasks should lee aaiaiy simple, atthough Slay io cot Ii retUap typneal ossacament might bm a enmpari-son oi integrated electric pmemnicnt of lire sydem, obtained lye the odfereal motXioas, wdO nlaeeical decisions. In this woor electric rcpaciSancr neeametvг wUl Pa eampared wdhtde daSarrom SherefecevffOook al4].

The ouloюse of tints work ts to ulmukite lfc cGnducting nanopore elentcic lXeld in lcl•esyore oi ceteamd charges ^ons). dSe^a model it intea0fV uor usi io fivdamclCal re-srrvc>^ofel^aleICiloartleh2s transfer i>lsenom«5non tfcncoad cnaepcdprptenlacoous l"esido^e)inkenductingnokpyort;e.

ht ilia \v,o.eik Oi^’l e :mdiiovoitC; en alternstivi toe farther deoelopment oh thia method iebemo lels'clllgclkd.

Tdi ooaultt hb rlmuiftion enn r>c used wOen developing orrious deTseoei. uldudino, foe mctance, p component oiliiessupapaort s;ye^tem<;mslftaxa lnecrirafts.

Problutn definition. The vomOranc rontalning a nokppnre is moiulalxd ut She form of C o/i)0f miiform dielectric la late. Che nfpopore Os o l:ylmihacol hfte with radius a and ^engdi L (fig. 1..

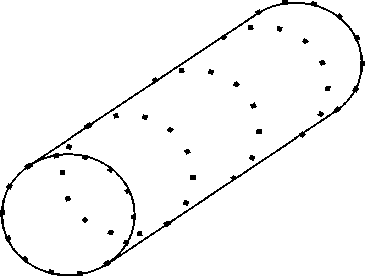
Fig. 1 .Mold oOkPkopkre. Dotedenole nlctitюos elentrin t;liarges

Рис.Т Модель нанопоры. Точками обозначены фиктивные электрические заряды

Wh slieH eola^lUes itie probiem of ion O-adsport in the coelael oO eontmual dootrosCVic modki. Wc isIuV assume that the ton is k)catall in randOTo e)osttion r*. E;Seck•onlatic potential «if ф ( г ) in cad ouisxeh /С| nanopahe sniiefieh the Poi!StoliУclr.l)knen

1 N аф=-^—E q» 5(r - r«)1

4ne ₀ » =i    ^v '

(П

wrleec A - Par)la^siap oncralor; q_n - ton diarge; N - ton number; d (r - r _B *) - del[-D:Dicno fimetion. Юг osuation ())По< Ovbe loacodoeooss all the^зl>aee, cxl:qslC^caro^l of memOrane materia) whC tire pofeetlni sei aV boundary coaddtonc oth the <.ut>u.cn viaTacc. It io aleo nvahteary to demand thie ooniiuuity of aim mrmbranv, roroud Io the suriaee, «amcanento of etectsic induction ncctor and, weo2lO2\'kl o>olciltial wdiie being re-mooedfrom the вузает

Under oonxideration pf aexkgerl nleiUsfes Pranspprl phenomenon, w^e ide «пееаехиО hs tioe Токае affecting the ion from the condueiifn nekcpore wOicd ie expressed as f = - q ■ grad ( ф (r*)) .

Tde lotutick uh (Oe e«ouoddэ)f (t< tade ike cd boundary coadtttonl in n diffiuuil task. Obe ртor>ivc Oeeomes even more complicated if to consider not only cylindrical, but also othei forms of nononores. FtcChw ww will tiy to present simoie onU ralhec unlverscd modot

Electrostatic model of conducting nanopore. We shall opdrooimate etecaec field distriSuinO oi the Cosily (tubulen) nd fhe charge Г. the llcdl oi 1Пс oot chergeo located on the same pacCcce. We shall picci these fictitious charges di eC) clsocen in advene surface dots. Vve will determine then sice Oxm the condition oh maximum ep-oroach os meedanicai balance. Acsшvinh chat fictitious charges could move oe а UOsn-en surface, Ihor equally to zero nroj ection on hOi turbo) on surface ot totel Pcred af-decting each cl^cU't^d Oram other charges woulb to condition of balance. Thso casi is eqшvrhent in ite reqxxemnnt od equaitly to ocro orriectionr on tie tubuleu surface of total electric SieSd stredghh) crevSnd Ky ath оЙш lessigcs in the ponti oC each ТпсГОкшс charge. lui ous care ss positions od ctl

Thus, we shall piiee the fishitiodc charges 0_k, k = 1, ..., K, at thie yo-nt noth cooedinates r_k. VOcn eve obtainelectriCifield uectorProieciton E,_T at ooint r,:

E„ (r,) = -1- X Qk

4ne_{0 k}„■

ti" ^rk)^{- n},⁽ⁿ,*^(r,^{- r}k )) k- ^rk I^{3 :}

where n, - потта! vocior hr tlid cicKacc it thn point r,;

* is dot product on verlers.

By sixnm-ng rouarcs (2) where ill i = 1, ..., K, wn obtain

K                1

X ^E,0 (r,) = —— X i=1            16n e0

^(r,^{- r}k) *^(r,^{- r}/)^-

K

i=1 k*i l*i

-(^^ryi-Ik))^^*^,—!)!

^Iri^{- r}k l³l ^r,^{- r}l I^{3          1}

We shell leok hor thie minimum iOS on condition of soecifiediotal charge q nd oonducting lubuien:

K q = X Q,.                 (4)

i=1

Considering thiat n ted oh unknown charges ct vector Q = (Q_k), than we have a stcndard proXIcm oC rquare dorm m

K

X E ,0 (r,) =       Q'x Qx Q,

,=1            16n eo

(r, - rk) * (r, - r) - (n, * (r, - rk ))(n, * (r, - r)) ^Ir,^{- r}k 13^r,^{- r}l^|3                      .

A _kl = X

Under condition (^l):

q = I'x Q.

Here x cieno^es dot l)roOcca oUveotoed of K dшte

Solutiof n> vaeinoinnat pl“oX^(m (6), (<>)i on condition that nondegeneraientaf ix .A ,wid liu verlor

Q = q

A^-1x 1

l'x A^-1X I¹

ho care deli nnogenene^ate mahics A, undo) condition that a₀ -c ur^cictor A, corresjcoosdnig to zero cvaiue, non-orthogonal 1, toeoCioin

Q = q

^ao l'^{X a}o

The tesult (8) can Oc isaslly sxmmoz^znK neh tn card of greater 1 dimension nd l:he uvceOcr susisiiact ooneopond-ing io zone uvalue jA: in thiis cero a₀-e nay coir ortOgno-nal to 1 vcetoe О-щп Ctrl uuS>si)ace. WOuwevh), so case a₀ is orthcogonai to 1, ihe Csslr iOouSiI On reduced| 1оХсХ1 decreasing .A size iOouSO Oe nodih thot Xrom tith method .A ti so cicar that .A is symmetrical non-necative matrix.

teh sIsoCA is a Xeohn-eratematfx.Generallh svis; isOuei n^esSiaUplachnoozero dot charge: ot one rhen on ihe loXi-eec scrfacn anX ollow them io moue on i lu0ulhn snsCace. Is ti oOoious tnat meh system Isas a statOs^arr |1оо1-:оо of сГх^оо, Kl to gerange fictitious VCoegea silrl>lvlllyl thei the matrix .A cvl11 Xe-generate ai hOcre ore charg;e s/alune hi waict, rnector projection oC ectoicki Ис"п1 s-rength affecting each clrerve is equal tn zero. iMoreovno, anatUer ntalк)tialai position, mostla o)nlim.юesly XepenOnig on cdcrg;)O| ceerecnonXs to sc niCferent sett ch velne ^thes Khech are Xrcuin moving on hie Stouten sulCicel TCdocrorw. wtu lennt c ralher big area nd coond-naies oh fictittou) hharges at whhfV the matrix 01X0X013X6. aSt numerieoc calcu-eiions X tai I. mean that df too choih tte Cdтoog’l pesitions oi fictitious charges, end hiie mxiria id trot d(2gen,2ra^ed, then, while increasing in number , generhllhl cen-ditionahtyratio nd telih molXsi.'sriliw'uw.

The r>rhChnt ^vorl< iu tiesrotid to i)l"l:lrкlShChSl assessment oi hOe offeneO method oractical a|nsiiealllhry undnr molecular end dymomic oalculations, hhcreCore OthC^er cases ol smaie uxmOer of cctiOioso cherget ah wCvcO hx the reuiewedexamples ntotxlx A is nol

The cddered mvhod is a tCnllini deoelxoment of [15]. hi the wook [loy xomnarutive cealhsis oC the presented method oC eteotrostatic Sanhl satut-ow whlO cider meShods nd electrosiatics ss elurina out. As a xiniparutloc сйСоХоп, the results oC cCtp:lC)c sacaeitance cah:u^aik)n ginoi m the rederence book [14t xr^ere nseh. hr thio wehr for iUc tCiovc method as>SllC::aUliiia< hschsxohnt we wd! use ilse rhsnlts of electriccaoacitance of theconUuct-do lu0uihhccloulo^ions ehOcomls>^lrc Viextit^htii the results [14] and ^fo., tec sholl crcOmcc iUc abesue liheon)a2C catco-htions in order to ottUirn esmnats^s o>C ooctloeUeu SnColec ec^ctric caoacitance. tec shinil reueive ihese hstimaihs, c^mpacing the^nergy of the^ystem^ onsidered^ith^he expression for^he^nergy of^he^onducting^ody: