Mathematical modeling of processes in quantum computer elements based on methods of quantum theory to improve their efficiency

Richard Feynman in 1982 proposed constructing computers from quantum mechanical elements as a means of improving computer and communication device performance [1]. Since then, active efforts have been made to create computers and other information devices based on quantum elements. The main components of a quantum computer are systems consisting of two identical qubits. Entangled states of two qubits are of fundamental importance in the operation of a quantum computer and in quantum information science (cryptography [2], teleportation [3]). However, in real constructions, qubits in an entangled state can only be maintained for a limited time. Therefore, active theoretical and experimental research is currently underway to find conditions that can prolong the time of quantum entanglement of qubits.

Quantum entanglement is important for understanding quantum theory and the prospects of its applications. Fundamental principles and primary methods of creating and detecting entangled states in various quantum systems can be found, for example, in the review [4]. Several dimensionless parameters have been introduced for quantitative measurement of quantum entanglement, such as the PG parameter [5], negativity [6], and state entropy [7].

In reference [8], the entangled states of cold ions confined in a linear trap and interacting with laser beams are discussed. It is shown that the decay of the entangled state in this system is negligible, and quantum register measurement (quantum reading) can be performed with high efficiency. Reference [9] considers the stabilization of the entangled state of two-level atoms interacting with a classical laser field with the consideration of spontaneous emission. The exact solution obtained shows that the optimal entanglement that can be achieved in the

Lamb-Dicke limit is 0.43. Reference [10] considers the decay of quantum entanglement of two-level systems, each interacting with a thermal reservoir at finite temperature. For a wide class of initially entangled states, the authors show that the system always disentangles in finite time.

References [11, 12] theoretically investigate the effect of dipole-dipole interaction on quantum entanglement and demonstrate the potential use of dipole-dipole interaction as a tool for controlling the degree of quantum entanglement. Reference [13] investigates the influence of chaotic behavior of coherent state parameters on the dynamics of entanglement in a system of two-level atoms and photons in a cavity. Reference [14] shows that the presence of a high-intensity laser field leads to a high degree of entanglement of two qubits. The paper [15] explores within the framework standard Tavis-Cummings model, entanglement of qubits under the influence of a non-stationary single-mode field and a Kerr-like medium. The work [16] examines the entanglement between two superconducting qubits in which there is a dipole - dipole interaction and interaction with the thermal field. The authors of article [17] analyze the dynamics of entangled states of qubits interacting with the external environment using the method of correlation functions. The paper [18] describes original experiments in which two molecules were presented in an entangled quantum state. A review of research on entangled qubit states allows us to conclude that the influence of an external electromagnetic field and dipole-dipole interaction between qubits is a promising tool for controlling the degree of quantum entanglement.

The article [19] notes the extraordinary progress in the modern development of quantum computing technologies, which indicates the prospect of widespread use of quantum computers.

In this work, we construct a mathematical model describing two interacting qubits with an external electromagnetic field. The model allows us to determine the PG entanglement parameter and its dependence on the qubit interaction parameters among themselves and with the external electromagnetic field. The density matrix and its evolution are determined in the energy representation within the framework of the path integral formalism. This formalism allows interactions of any intensity to be considered.

Mathematical model of two qubits interacting with each other and an electromagnetic field

We will construct a mathematical model of a system in which two qubits interact with an external electromagnetic field and with each other, and determine the degree of entanglement of the qubit states as a function of the interaction parameters. By varying these parameters, we can alter the degree of entanglement of the qubits.

The Hamiltonian of this model is given by:

л          л       А               А          А .        А

Hfuii = Hq + V(t), V(t) = Vqf (t) + Vqq ,        (1)

where Hq - Hamiltonian of two non-interacting qubits; V QF ( t ) — interaction operator between qubits and the electromagnetic field; V QQ – dipole-dipole interaction operator of qubits with each other.

We describe the studied system by the statistical operator p in the interaction representation [20]:

p ( t ) = и d ( t ) p (0) u d ( t ),

where

t

i

UD ( t ) = Г exp -- V D ( t ) d t ,

t

V d ( T ) = exp

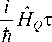
тУ / \

V ( t ) exp

-

ˆ

У HQ T Й

where T is time-ordering operator.

The explicit form of the statistical density matrix will be calculated in the energy representation [21]. To achieve this, we will take the eigenstates of the two-qubit Hamiltonian as the basis with the following properties:

HI _e | n , m > = E „_m | n , m > ,

^ | n , m X m , n |=1,                             (3)

n , m =0

= 5n-n5m■ n, where En,m = En + Em is the energy of the noninteracting qubit system; |n, m> = |n>®|m> are the eigenstates of the two-qubit Hamiltonian, they describe the state of the system; each eigenvector | n>, | m> takes two values, i.e., n = 0,1, m = 0,1. In this basis, equation (3) takes the form of equation (2).

^  pm n f m. (O)( minnin | UD (t) | nfmf >, f f f f                                                                    minninninmin nin,nin=0min,min=0

where pmfnfnfmf (t) = , p» „ n m (0) = . minninninmin

The kernel of the evolution operator is computed based on the summation over all possible trajectories in the energy space:

< m f , n f | U D ( t )| n in , m in > =

^{11 K}              (5)

= E E П < m k , n k | U d (t k , t k -1 )| n k -1 , m k -1 > , n 0 ,.,n_K -1=0 mo ,.., ^mK —1=0 k =1

with t k >  t k– 1 and n 0 = n in , m 0 = m in at the initial time t 0 =0 and n K = n f , m K = m f at the final time t N = t >0.

The computation of the matrix elements of the evolution operator <  n f , m f | U_D ( t )| n_in , m_in >  based on equation (5) will be more accurate the smaller the time intervals t k – t k– 1 we consider.

Based on equations (4), (5), we will establish recursive relations for the matrix elements of the statistical operator at different time points:

p ' ' ( tk ) = m_kn_kn_km_k^k

= E E    < m k , n k | U d ( t k - t k -1 )| n k —1 , m k —1 >x (6)

ⁿk -1- ⁿk -1=0 ^mk -1- mk -1=0

xpm, ,       ,rn, ,(tk-1), mk-1 nk-1 nk-1 mk-1

where the statistical operator is normalized at each time moment, i.e., Sp p ( t ) = 1.

Equations (4–6) represent an algorithm for calculating the statistical density matrix p _n fmfn‘f m'f ( t ) at any time moment t .

For small ( t k – t k– 1 ) the evolution operator Û D ( t k – t k –1 ) according to (2) can be represented as

ˆ

^UD ⁽ t k , t k -1 ) =

= 1 - — I exp П-H q t V ( t ) exp

-

l _л_ iHQ -

A t ,

Й

where A t = t_k - t_k — 1 , t = 1/2( t_k + t_k — 1 ).

Based on (3), (7), we can express the kernel of the evolution operator (8) as:

< mk, n ,| U0 (tk, tk-1) | n-1, mk-1 > ^ 5 nknk-1 5 mk, mk-1 + i                                                          (8)

+-exp|j(©nknk-1 +®mkmk-1 )_|At, where Й©    = E - E , Й®    = E - E , k k 1 k k 1 k k 1 k k 1

i.e., ю„,„, ,, cd„, , are the transition frequencies of the nknk -1       ^mk^mk -1

qubits between their states.

It is clear that the adjoint matrix of the evolution operator is also constructed in the same way < m k -1 n k -1 1 U 0 ( t k -t_k -1 ) | n k m k > .

Note that for physical models, constructing the evolution operator (9) in explicit form for a small time interval ( t k – t k– 1 ) is much simpler than constructing the evolution operator < m k , n k | Ud ( t k , t k -i )| n k -1 , m k -1 ) for a finite time interval ( t k – t k– 1 ).

The explicit form of the statistical matrix is constructed based on the recurrence relation (6). For this purpose, we specify an explicit form of the statistical matrix at the initial moment of time p m in n in n' in m' in (0), a transition matrix (9) over a small time interval ( t k – t k– 1 = t ) and in accordance with equation (6) we obtain the statistical operator p m in n in n' in m' in (t) at the moment of time t (with the normalization condition Sp p ( t ) = 1). Applying recurrent relation (6) N times, we will construct an explicit form of the statistical operator p _m f _m '_f (t), for a point in time

N t = ^(tk - tk-1), t0 = 0, tN = t . k=1

This method is convenient for numerical calculations. Calculation accuracy increases with shorter time intervals ( t k – t k– 1 ).

To quantitatively assess the quantum entanglement of the two qubits, we use the PG parameter [3, 4] with the measure s :

s ( t ) = £ (|M t )|-M t )),                        (9)

i =1

where X i - are the eigenvalues of the following equation:

det ( < m f , n f | p ( t ) | n_f ', m_f ') ^pT -X I) = 0,             (10)

where ф ₁, ф ₂ - are the phases of oscillations of the electromagnetic field acting on the first and second qubits, respectively.

The matrix elements of the evolution operator (8) considering (1), (11), (12) take the form

where I is the identity matrix; the index pT denotes matrix partial transformation. The entanglement is maximal when s = 1 and minimal when s = 0.

The explicit form of interaction potentials Vqf( t ) , Vqq is constructed based on the physical model. The proposed system of equations (6), (8), (9), (10) allows one to numerically generate plots depicting the dependence of s on the qubit interaction parameters and parameters of the external electromagnetic field.

Numerical modeling of entangled states of two qubits

Based on the proposed mathematical model, we describe the entangled states of two identical qubits in a specific physical model.

Consider a system of two qubits, in which the interaction operators are represented by the following expressions.

The operator V QQ of qubit dipole-dipole interaction:

V QQ = gd 1 d 2 , (11)

where d ^ˆ ₁ , d ^ˆ ₂ are the operators of the dipole moments of the first and second qubits, respectively, and g is the interaction constant.

The operator V q_F ( t ) of qubit interaction with a single-mode electromagnetic field with amplitude E ₀ and frequency Q :

V q_F ( t ) = d₁E ₀ cos ( Q t + ф ₁ ) + d₂ E ₀ cos ( Q t + ф ₂ ) , (12)

< m k , n_k | U d ( t _k , t k -1 ) | n k -1 , m k -1 ) = 8 nk , nk _{- 1}8 mk , m_{k - 1} +

' ' ^ < m k , n k | d 1 < d 2 1 n k -1 , m k -1 ) exp [ i ( й nknk _{- 1} +® m_km_{k - 1} ) t]A t +

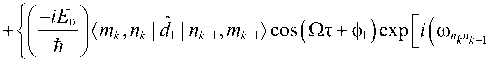
^{+ й m}k^mk -1 ^)t] ⁺

1 - iE 0 11 +1 —^— l< m k , n_k\d2\n k -1 , m k -1 ) cos ( Qт + ф 2 ) exp [ 1 ( й nknk _{- 1} +® m _k m _{k - 1} ) tJ^A t .

We also construct the expression for

< n k -1 m 'k -1 1 U D ( t k - t k -1 ) | nm ) .

Let’s number our basis vectors in the following order:

| n k -1 , m k -1 )Ч 0,0 ) ,\0,1 ) ,\1,0 ) ,\1,1 ) ,                 (14)

< m_k , n k H< 0,0|, < 1,01, < 0,11, < 1,1|. (15)

In this basis representation, we express the matrix of the evolution operator with elements (13) explicitly for the case when Q = й :

1 - i ORAL e+-Ф2 2 _ iQ R At e+iФ1 2 0 < mk, nk | Ud (At)| nk-1, mk-1) = -i QrA1 e-Ф2 2 -i QR At e-iФ1 2 1 - i Q q A t -1 QrA e+-Ф1 2 - i QR A t e+iФ2 2 ,                       (16) - iQ q At 1 0 к - iQ R A t e-Ф1 2 t - i——e - ‘ ф2 2 1 l where At = tk- tk- 1, QR = dE0/h is the Rabi oscillation frequency, Qq = gd2 / h is oscillation frequency for qubit interaction, d is absolute value of qubit dipole moments 〈nk |d̂ |nk–1〉 = d1(1 – δnk, nk–1), 〈mk |d̂ 2|mk–1〉 = d2(1 – δmk, mk–1), absolute values of dipoles are equal to each other d1= d2 = d. We took into account ωnm >0 for n > m, ωnm <0 for n < m and ωnm =– ωnm. Terms with frequencies Ω + ω, 2ω01, 2ω10 are neglected when we construct (16) in rotating wave approximation.

The corresponding structure has the adjoint matrix. In our modeling, we assume φ 1 = φ 2 =0.

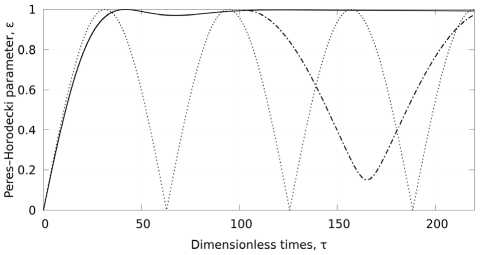
Fig. 1. The dependence of the PG parameter on the dimensionless time parameter

The fig. 1 represents the results of numerical modeling of the dependence of the PG parameter ε of our model on the dimensionless time parameter τ = Ω 0 ⋅ t and interaction parameters Ω R and Ω Q . Where Ω 0 is constant that has the dimension of frequency and must be specified when considering specific experimental conditions.

The first numerical experiment was conducted with the qubit dipole-dipole interaction enabled ( Ω Q = 0.05 ⋅Ω 0 ) and in the absence of an external electromagnetic field ( Ω R = 0.00 ⋅Ω 0 ). The graph depicting the dependence of the PG parameter on time is shown as a dashed line. The results indicate continuous oscillations of qubit entanglement in this case, as the PG parameter ε oscillates from the minimum value of 0 to the maximum value of 1.

The second numerical experiment was conducted with the qubit dipole-dipole interaction enabled ( Ω Q = 0.05 ⋅Ω 0 ) and in the presence of an external electromagnetic field ( Ω R = 7.50 ⋅Ω 0 ). The results indicate oscillations of qubit entanglement, which stabilize at a state of high entanglement when the PG parameter takes a value of around 0.99. Note that an external field with a smaller amplitude changes the value of the entanglement parameter, but does not establish its stable value.

In the third experiment, the external electromagnetic field ( Ω R = 7.50 ⋅Ω 0 ) is turned on at the moment τ =0 and turned off the moment τ = 100. Turning off the field leads to a decrease parameter ε and the destruction of the entagled state. A graph of this behavior ε over time is presented with a dash-dotted line.

Conclusion

The proposed mathematical model allows for the study of the entanglement parameter ε of a two-qubit system for different interaction potentials.

It is shown that the interaction between qubits leads to the entanglement of their states. Additional interaction with an external field leads to the stabilization of the entangled state.

The proposed mathematical model allows for the exploration of entangled states of qubits under the influence of external fields of any structure.