Матрица жесткости конечного элемента пространственной балки с низкой тансверсальной сдвиговой жесткостью

Автор: Нестеров Владимир Анатольевич

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 3 (29), 2010 года.

Бесплатный доступ

Разработан конечный элемент балки, в расчете которой учитываются трансверсалъные сдвиговые деформации. При вариационной реализации метода конечных элементов получена матрица жесткости пространственной балки. В качестве одних из основных узловых кинематических параметров присутствуют углы трансверсального сдвига

Балка, метод конечных элементов

Короткий адрес: https://sciup.org/148176255

IDR: 148176255

Текст обзорной статьи Матрица жесткости конечного элемента пространственной балки с низкой тансверсальной сдвиговой жесткостью

В по следние годы все чаще композитные конструкции используются в производстве космической техники. Композиты обладают высокой удельной прочностью и жесткостью, а также способностью к направленному изменению механических свойств в соответствии с назначением и условиями эксплуатации конструкции. В частности, космические антенны представляют собой композитные рамные конструкции балочного типа. Вместе с тем композитные конструкции, в том числе и балки, отличаются рядом особенностей, которые должны быть учтены при проектировании и расчете. Основная среди них – низкая сдвиговая жесткость по отношению к трансверсальным напряжениям. Учет указанной особенности при реализации численного (конечно-элементного) расчета приводит к повышению порядка разрешающих уравнений за счет введения в рассмотрение углов трансверсального сдвига. Это обстоятельство от- личает матрицу жесткости, полученную в работе, от традиционных балочных конечных элементов.

Рассмотрим пространственную задачу об изгибе слоистой балки с низкой жесткостью при трансверсальном сдвиге. Для решения воспользуемся вариационным алгоритмом метода конечных элементов. Уравнения равновесия конечного элемента балки получим вариационным методом, для этого выделим элемент длиной l и запишем для него выражение полной потенциальной энергии

E = U + П, (1)

где U – потенциальная энергия деформации; П – потенциал внешних сил.

В качестве исходного для U возьмем соответствующее выражение из линейной теории упругости трехмерного тела:

^U = ¹ Л!' ^a x e x ^+С y e y ^+С z e z ⁺ 2 _V

^{+ Т} xy e xy ^{+ Т} yz e yz ^{+ Т} xz e xz ) dxdydz ,

где V - объем элемента балки; a x , а y , а _z - нормальные напряжения; т x , т x , т yz - касательные напряжения; e x , e y , e_z – линейные деформации вдоль осей системы координат; e_xy, e_xz, e_yz – деформации сдвига в соответствующих плоскостях.

Будем полагать, что главные направления ортотропии материала совпадают с осями локальной системы координат, ось X которой совпадает с продольной осью балки, а две другие ( Y и Z ) составляют с первой декартову систему.

В этом случае физические соотношения, представляющие собой закон Гука для ортотропного материала, имеют следующий вид:

а x .. a y .. a z

ex e цxy e цxz e ’ xyz

G У G x° ey = ^^yx^^yzE ’ yxz az a x ez = ET "ц zxE "ц zyE" ’ zxy т xy exy = GT ’ xy

_ т yz eyz G ’ yz т x e = G",(8)

xz где Еx(y, z) – модуль упругости соответствующего направления; Gxy (yz, xz) – модуль сдвига в соответствующей плоскости; цx, цyx, цyz, цzy, цxz, цzx - коэффициенты Пуассона.

Имеет место свойство симметрии упругих постоян ных:

^E x ц xy = ^E y ц yx ; ^E x ц xz = ^E z ц zx ; ^E y ц yz = ^E z ц zy . (9)

Запишем геометрические соотношения линейной теории:

du, ex = , dx (10) dUy ey = ^“, dy (11) d uz ez = , dz (12) e xy = d Ux S Uy dy dx ’ (13) eyz S Uy d uz = —- + —-, dz dy (14) exz dm. 5 u, = —- + — 5z 5x (15) где ux, uy, uz – проекции перемещения произвольной точки на соответствующие оси координат.

Введем в физические соотношения следующие допу щения [1]:

^E y ^^ ; ^E z ^^ ; ц yx = 0; ц zx = 0; G yz ^” . (16)

Тогда вместо выражений (10), (11), (12) и (14), соответ- ственно, получим:

e =G x x _Ex ^,	(17)
e y = 0,	(18)
e_z = 0,	(19)
e yz = 0.	(20)

С учетом формулы (18) из выражения (11) следует, что перемещения uy не зависят от координаты y. Аналогично, из выражения (12) с учетом формулы (19) следует, что перемещения uz не зависят от координаты z:

U y = v ( x , z ) , (21)

U z = w ( x , y ) . (22)

Согласно гипотезе плоских сечений имеем следующие законы распределения нормальных (к упругой линии балки) перемещений:

U y = v ( x ) - z p ,

U z = w ( x ) + y p , (24)

где v ( x ) и w ( x ) – соответственно, перемещения вдоль осей Y и Z точек, лежащих на продольной оси балки X ; в – угол поворота сечения относительно оси X .

Согласно той же гипотезе имеем следующий линейный закон распределения по сечению продольных перемещений:

u x = ^u ⁽ ^x ) ⁺ у ⁹ y ⁽ ^x ) ⁺ ^z ⁹ z ⁽ ^x ), (25)

где u ( x ) – перемещения вдоль оси X точек, лежащих на этой оси; 9 _y , 9 z - углы наклона сечения к соответствующим координатным осям.

Подставляя выражения (23)–(25) в геометрические соотношения для деформаций сдвига, можно увидеть, что выражение (14) удовлетворится тождественно, а вместо формул (13) и (15) получим следующие выражения:

e xy

„ dv d В 9„ + z —, ^y dxdx

„ dw d P e„ = 9, + — + y—. xzz dxdx

Подставим выражение (25) в формулу (10) и получим выражение для продольных деформаций:

dU d 9 y d 9

ex = — + У —- + z—- . dxdxdx

По аналогии с задачей об изгибе балки в плоскости введем в рассмотрение осредненные деформации трансверсального сдвига, которые определяются по следующим формулам:

V y =9 y + —, dx dw

V. = 9, + — . zz dx

Перепишем выражение для потенциальной энергии деформации (2) с учетом принятых допущений (18)–(20).

^U = ¹ Ш ⁽ ^a x e x ^{+ т} xy e xy ^{+ т} xz e xz ) ^dxdyd^z . 2 _V

Подставляя в подынтегральное выражение (31) в соотношения для деформаций (26)–(28), получим:

U =

du ^d 9 _y d 0, — + y —- + z—^zdxdxdx

L dv d P) V _ dw d P)| , , ,

+т„ 0„ +--- z— + т1 0_z +--+ y— ddxdydz .

xyyxzz

V dx dx J V dx dx JJ

Если использовать физические соотношения (17), (6) и (8), то выражение (31) можно представить в следующем виде:

U = 1 Ш (Exex + Gxyexy + G e2 )dxdydz’(33)

2 V а выражение (32) в виде

1 г г г Г dud

U =- 1 E x I — + y—-

2J VJ V dxdx d^ T dx J

_ In dv

⁺ G xy I ⁰ y ⁺ "Г

V dx

z d ₽Y+r z — + Gxz xz dx J

n dwd

0z + — + y— I >dV. dxdx

Произведем в выражении (32) интегрирование по пло щади поперечного сечения балки. В результате получим следующее:

^U = ¹ J

² ( x )

L.du d0yd

N + M + Mz+ dx dxdx

⁺ M yz d ^ ⁺ ^Q y V y ⁺ ^Q z V z

V dxJ dx,

где

N = J J ^CT x dydz ;

( y )( ^z )

M y = J J y ^CT x dydz ;

( y )( ^z )

M z = J J ^z ст x dydz ;

⁽ y ⁾⁽ ^z )

^Q y = J J ^T xy^ ^;

⁽ y ⁾⁽ ^z )

Q z = J J^T xz dydz ;

⁽ y ⁾⁽ ^z )

^M yz = J J ( ^T xz y ^T xy z ) dydz .

⁽ y ⁾⁽ ^z )

Заменяя в выражениях (36) напряжения стx, тxy и тx их значениями, найденными из соотношений (17), (6) и (8), в которых, в свою очередь, деформации ex, exy и exz учтены согласно выражениям (28), (26) и (27), получим физичес- кие соотношения в виде

N = Bd + ' " + C ₂ d ° z ;

dxdxdx

Q y = K , V y + C 4 d P ; Q z = K 2 V z + C 5 d ^p ; dx dx

M_y = C du + D^ + C ₃ d°- ; ^y dxdxdx

Mz = C ₂ du + C ₃ d ° + D ₂ d⁹^ ;

dxdxdx

Myz = C4 V y + C5 V z + D.2 d^, dx где B, C, D и K - параметры жесткости, вычисляемые по следующим формулам:

B = J J Edydz ; C 1 = J J y Edydz ;

⁽ y ⁾⁽ ^z ) ⁽ y ⁾⁽ ^z )

C ₂ = J J zEdydz ; C ₃ = J J yzEdydz ;

⁽ y ⁾⁽ ^z ) ⁽ y ⁾⁽ ^z )

^C 4 = J J zG xy dydz ; ^C 5 = J J yG xz dydz ; ⁽ y ⁾⁽ ^z ) ⁽ y ⁾⁽ ^z )

D 1 = J J y ² Edydz ; D ₂ = J J z ² Edydz ; ⁽ y ⁾⁽ ^z ) ⁽ y ⁾⁽ ^z )

^K 1 = J J G xy dydz ; ^K 2 = J J G xz dydz ;

⁽ y ⁾⁽ ^z ) ⁽ y ⁾⁽ ^z )

D 12 = J J ( y ² G xz + z ² G xy ) dydz .

⁽ y ⁾⁽ ^z )

Примем для продольных перемещений оси стержня u , угла поворота сечения относительно оси X ( в ) и углов трансверсального сдвига V линейный характер изменения вдоль оси, а для прогибов обоих направлений - кубический:

u ( x ) = a 1 + a ₂ x ; v ( x ) = a ₃ + a ₄ x + a ₅ x ² + a ₆ x ³ ;

w ( x ) = a ₇ +a ₈ x + a ₉ x ² +a ₁₀ x ³; (39)

V _y ( x ) = a ₁₁ + a ₁₂ x ;

V _z ( x ) = a ₁₃ +a ₁₄ x ; в ( x ) = a ₁₅ + a ₁₆ x .

Изменения вдоль оси X углов поворота сечения по причине изгиба будут определяться по формулам dv „ . 2. dw „ .2

— = a₄ + 2a₅ x + 3a₆ x ; — = a₈ + 2a_g x + 3a,_o x . (40)

dxdx

Сформируем вектор кинематических переменных:

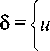
dv v dx

dw w — V y V z dx

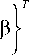
Тогда уравнения (39) можно записать в виде следую- щего матричного выражения:

8 = S^ a,(42)

где a - вектор постоянных:

a = { a 1

^a 2

a3 a4 a5 a6 a7

a9 a10 a11 a12 a13 a14

^T ^a 16 } >

S - матрица со следующей структурой и компонентами

	'	x	0	0	0	0
	0	0	1	x	x ²	x ³
	0	0	0	1	2 x	3 x
S =	0	0	0	0	0	0
S =	0	0	0	0	0	0
	0	0	0	0	0	0
	0	0	0	0	0	0

0 0 0 0

1 x x ² x ³

0 1 2 x 3 xx

0 0 0 0

1 x 0 0

0 0 1 x

0 0

^{0 0}
0 0	- (44)

0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 x

Введем в рассмотрение векторы узловых кинемати- ческих параметров:

- в первом узле:

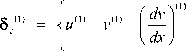
- во втором узле:

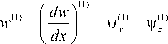
в" ) [ ; (45)

8 e ^l2> = 1 u ^l2) v ^l2) V dx 7* w^m V dw 7 ^ ^V ’ ^2> в[' (46)

Через 8 e обозначим вектор узловых кинематических параметров балочного элемента:

δ _e ={ δ _e ⁽¹⁾ δ _e ⁽²⁾ } ^Т .

Компоненты вектора δ _e найдем с помощью соотношения (42), которое следует записать для двух значений продольной координаты: X = 0 и X = l ( l – длина балочного элемента). Результат запишем в матричном виде:

δ _e = T ∙ a ,

xx ²

P3,10 = P5,12 = 6 ~p — 6 JT ’ xx2

^P 3,11 ^P 5,13 ² l ^{+ 3} 1 2 .

Матричное соотношение (49) в развернутом имеет следующее представление:

виде

где Т - матрица размерностью 16 x 16 со структурой и компонентами, приведенными ниже.

Подставляя вектор a , найденный из выражения (48), в уравнение (42), получим значения компонент вектора δ , выраженные через узловые кинематические параметры:

I X X I | -X X v = 1 — 3 — + 2 v+ x — 2— ■

dv Y') dx J

где

δ = P ∙ δ , e

P = S ∙ T ^–1 , где T – квадратная матрица следующего вида:

dv dx

T =

+ | 3 ^ — 2 ^ I v⁽²⁾ I 1 2 1 3 J

x ² x ³ II dv Y²⁾

l l ² JI dx J

£ X X^х I (1) I 1 л X X^х

—6— + 6— vu' + 1 — 4- + 3— l2 l3 J I l l2

dv I dx J

2 t

3 t ²

t ²

2 t

t ³3 t ²

0 0

Матрица Р имеет размерность 8 x 16. У нее щие структура и компоненты:

следую-

P =

^p 11

^p 32 0

^p 23 ^p 33 0 0

^p 19 0

^p 44

^p 54

^p 45

p ₆₆0

^p 3,10 0

^p 3,11 0

^p 4,12

^p 4,13

p ₇₇

^p 88

^p 8,16

P 11 = P 66 = P 77 = P 88

= 1 — - ; I

^P 19 = ^P 6,14 = ^P 7,15 = ^P 8,16 = у >

22(2)

I , X X^х \ m I X^х 3 - II dv I

+ 6— — 6— v ⁽²⁾ + — 2- + 3— —

I l ² l ³ J I l l ² JI dx )

I -X „X I | -X X w = 1 — 3 — + 2 — w + - — 2 — + —

' 2 1 ³ J I ll ²

dw I dx J

+| 3 ^ — 2 ^ I w ⁽²⁾I 1 2 1 3 J

dw dx

23 (2)

x x 11 dw I

"T + II I l l JI dx J

22(1)

, x X^х \ m I 1 л X X^х \l dw I —6 — + 6— w + 1 — 4- + 3— —

1 ² /3 I /2 UxJ

22(2)

I _r X X^х I (2) I X^х X^х II dw I + 6 — — 6— w ^w + —2— + 3 — —

/² 1 ³ I 2 Mx)

V y = I 1

V _z = | ¹

U = I 1 —

V *”

(2) ^y

P <ⁿ + ^- P <²⁾ ,

- I u ⁽¹⁾ + -u <²⁾

I J l

P 22 = P 44 = ¹ ^— ³ I T ⁺ ² "p»

23 x ² x ³

P 23 = P 45 = ^X ^— ² у ⁺

Подставим соотношения для кинематических переменных (51)–(58) в выражение потенциальной энергии деформации (34), выполним интегрирование и полученную функцию продифференцируем по каждой из компонент вектора узловых переменных δ _е . В результате получим матрицу жесткости балочного элемента со следующими компонентами и структурой:

k 11 = — k 19 = k 99 = Bl ;

к = — к _ = — к = к . — к -

13 л16 ^1,11 ^1,14 л39

= к = к ^ 69 ^9,11

— i

■к =

9,14 ⁼

C 1

;

p 2,10 p 4,12

p 2,11 p 4,13

= 3 ^ — 2 ; l ² l ³

x ² x ³

= ^— T ⁺F’

к = — к _ = — к = к

15171,131,15

—к _ = k__ = k_ =

59 79 9,13

— 1

■к_ = ^л 9,15

;

xx ²

P 32 = P 54 = —6 JT + 6 yi xx2

P 33 = P 55 = ¹ ^— ⁴ J ⁺ ³ j T>

D ₁ D ₁

22 ^2,10 ^10,10 ^±z- 1 3 ’ ^33 ^11,11 l ’

k 23 k 2,11

— 1

D ₁ C ₃

"k 3,10 = ^k 10,11 = ⁶ [ ₂ ; k 35 = k 11,13 = ⁴ [ ’

к — — к — — к — к tv 24 Л-2,12 л.4,10 а-10,12

= 12 — ³ * к = 2 — — *

l³ ’ ³¹ 2 l ’

к — к tv 25 Л-2,13

^к 3,4

—к . = — к

3,12 39

= ^к 4,11

—к =

5,10

—к = — к

10,13 ^11,12

= ⁶ C-^:

к = — к = — к = к

36 а-3,14 л₆,11 л_п,14

D 1

I ’

- к , , 0 к„ 0 к„ к ,6 к „ 0 к„ 0 к ,,11

^k 22 ^k 23 ^k 24 ^k 25⁰⁰⁰⁰ ^k 2,10 ^k 2,11 ^k 33 ^k 34 ^k 35 ^k 36 ^k 37⁰ ^k 39 ^k 3,10 ^k 3,11 ^k 44 ^k 45^{000 0} ^k 4,10 ^k 4,11

L L L Г) к к к ^k 55 ^k 56 ^k 57⁰ ^k 59 ^k 5,10 ^k 5,11 ^k 66 ^k 67 ^k 68 ^k 69⁰ ^k 6,11 ^k 77 ^k 78 ^k 79⁰ ^k 7,11 k 000 88

^k 99 ⁰ ^k 9,11

^k 10,10 ^k 10,11

^k 11,11

^к 3,13 = ^к 5,11 = ² C^ ; (59)

^к 37 = - ^к 3,15 = ^к 5,6 = - ^к 5,14 = - ^к 67 = ^к 6,13 =

C ³

^л 6,15 ^7,11 ^7,14 ^11,15 ^13,14 ^14,15 ₇ ;

^к 44 ^к 12,12 ¹² i з ’

^k 45

= к = — к . = — к .

л 4,13 ^5,12 ^12,13

= ⁶ т ■

^k 55

D ₂

13,13 i ’

к = — к = — к = к

575,157,1313,15

D 2 l ^;

5,13

= 2 '; l

к = к

* 66 ^14,14

DKl

— +—;

l 3

к = — к = к = — к = к =

Л 68 ^6,16 Л7,8 ^7,16 Л8,14

С + С

=-к=-к C4 + C5 - л 8,15 ^14,16 ^15,15 д ;

^k 6,14

^D 1 ^K 1 ^l

Г ⁺ ~^; ^к 77 = ^к 1

l 6

^D 2 ^K 2 ^l =^_+ v^;

^к 7,15 =

D2 K2l l 1 6~ ; к88 = -к8,16 = к16,16

^D 12 l ^;

П к к к 0k1,13k1,14k1,15 k2,12 k2,13

k3,12 k3,13 k3,14

k4,12 k4,13

к к кк k5,12 k5,13 k5,14

⁰ ^k 6,13 ^k 6,14 ^k 6,15 ⁰ ^k 7,13 ^k 7,14 ^k 7,15 ⁰⁰ ^k 8,14 ^k 8,15 ⁰ ^k 9,13 ^k 9,14 ^k 9,15 ^k 10,12 ^k 10,13 ⁰⁰

к к к к

^k 11,12 ^k 11,13 ^k 11,14 ^k 11,15
^k 12,12 ^k 12,13 ⁰⁰
^k 13,13 ^k 13,14 ^k 13,15
^k 14,14 ^k 14,15

^k 15,15

k 6,16 ^k 7,16 ^k 8,16 0

к k14,16 k15,16 k16,16

Матрица жесткости (60) является матрицей коэффициентов разрешающей системы линейных алгебраических уравнений, возникающей в задачах прочностного расчета пространственных балок, в которых она должна быть дополнена вектором узловых нагрузок. Эта же матрица фигурирует в задаче об устойчивости балки и в модальном анализе (определение частот и форм собственных колебаний).

Таким образом, получена матрица жесткости балочного элемента, предназначенная для конечно-элементного анализа пространственных балок, податливых при трансверсальном сдвиге. Она может быть использована как в расчетах отдельных балок, так и в расчетах стержневых конструкций рамного типа, деформирование которых происходит без депланации сечений.

Статья обзорная