Матричная технология измерений. Путь к нанометрам

В современной фотолитографии используются методы прямой записи без маски, которые позволяют обойти дифракционный предел и достичь разрешения менее 10 нм. Для реализации этих методов необходимо измерять линейные перемещения на уровне нанометров и угловые повороты на уровне сотых долей угловой секунды. Чаще всего используются различные гомодинные и гетеродинные интерферометры, которые позволяют достичь субнанометровой точности при измерении линейных перемещений [1 –3] и до тысячных долей угловой секунды при измерении угловых перемещений [4]. Однако на схемы измерения интерференции влияют различные факторы, которые приводят к существенным ошибкам. К таким погрешностям следует отнести влияние изменения параметров среды, через которую световые пучки в плечах интерферометра, а также нелинейность характеристики, обусловленная нежелательными отражениями. Применение двухчастотных схем не позволяет полностью исключить указанные погрешности [5–7].

Применение КМОП- и ПЗС-камер для решения задач измерения линейных и угловых координат широко распространено в различных областях техники [8]. При этом часто используется измерение смещений естественных объектов [9], но наилучшие результаты достигаются при применении специальных меток [10– 12]. Регистрация с помощью КМОП-камер звездного неба создала возможность и привела к широкому использованию приборов звёздной ориентации и развитию астрокорректоров космических аппаратов [13]. Точность таких приборов находится на уровне единиц и долей угловой секунды. Измерение длин объектов с помощью видеокамер производится в оптических экстензометрах с погрешностью на уровне 0,1 мкм [14].

Технология матричных измерений угловых и линейных перемещений в фиксированной плоскости, предложенная авторами [15–17], основана на использовании измерительной марки с десятками тысяч элементов. Простейшая измерительная марка представляет собой множество элементов круглой формы в виде двумерной периодической структуры. Конфигурация марки вклю- чает также 3 опорных элемента большего диаметра (рис. 1), позволяющих обеспечить как измерения углов поворота марки в диапазоне 0–360о, так и ее смещение в пределах поля зрения видеокамеры.

Рис. 1. Фрагмент изображения марки с опорными элементами

Видеокамера с объективом располагается так, чтобы движение марки происходило в плоскости, перпендикулярной его оптической оси, то есть параллельно фотоприемной матрице.

В процессе обработки изображения марки, полученного помощью цифровой видеокамеры, определяются координаты ее элементов, по которым вычисляется смещение марки и ее угол поворота. Также вычисляется масштабный коэффициент (период марки). При вращении или перемещении плоскость марки может наклоняться относительно оптической оси, вызывая искажение ее изображения. Эти искажения, как и искажения, связанные с дисторсией объектива и ошибками изготовления марки, корректируются [18]. Изменение масштаба, связанное с перемещением марки вдоль оптической оси, и искажения, вызванные наклоном марки, также позволяют измерять соответствующие координаты марки. Однако в этой статье мы ограничимся плоским движением.

Для новых измерителей прогнозируемая погрешность находится на уровне долей нанометра в линейной шкале и тысячных долей угловой секунды в угловой шкале. Очевидно, что получение такой высокой точности является непростой задачей, поскольку требует высочайшего уровня температурной стабилизации и деформационной стойкости конструкции прибора. Подобные измерители находятся в настоящее время в стадии исследований и разработок.

Важным фактором, также влияющим на точность измерений, является наличие шумов на получаемом с камеры изображении. Ограниченная разрядность изображения (шум квантования) приводит к ошибкам в определении координат элементов. Однако тепловой шум, присущий всем фотоприемным матрицам, превращает эти ошибки в случайно изменяющиеся во времени.

Экспериментальному и теоретическому исследованию случайной составляющей погрешности и посвящена данная работа.

• 1.    Теория

При отсутствии конвекции и вибраций основное влияние на СКО (стандартную неопределенность типа А) результата измерения оказывает погрешность определения координат элементов марки и число этих элементов. Случайный характер этой погрешности определяется погрешностью вычисления координат элемента вследствие пространственной дискретизации и яркостного квантования изображения марки и шумами камеры. При этом шумы камеры в разумных пределах играют полезную роль: каждый кадр оказывается независимой реализацией случайного процесса, и усреднение позволяет нивелировать влияние квантования.

Рассмотрим, как параметры марки и камеры влияют на погрешность измерения угла поворота, координат и периода марки.

• 1.1.    Угол поворота

Пусть изображение марки на матрице камеры образует сетку пятен с шагом H . Тогда координаты пятен марки, повернутой на угол ф , будут

X n = a_xi - a y j + b x ,

У п = a y i + a x j + b y ,

где i, j – номера строки и столбца n-го элемента марки, xn, yn – его координаты на матрице камеры, ax=Hcos ф, ay=Hsin ф. Уравнения (1) удобно записать в комплексном виде rn = akn + b, rn = xn + iyn, kn = in + ijn, a = Heiф.

В дальнейшем удобно использовать центрированные переменные

Гп = Г — (r), kn = kn — (k), где < > обозначает усреднение по всему множеству обрабатываемых пятен. В дальнейшем будут использованы только центрированные переменные, поэтому тильду в обозначении опускаем.

Все rn и kn можно рассматривать как компоненты комплексных N-мерных векторов r и k, тогда система (1) может быть записана как ak + b = r.                                       (2)

Переопределенная система (2) может быть решена методом наименьших квадратов.

a = ( kr )/( kk ) , b = 0 .                             (3)

Здесь

( kr ) = X к П r n

– скалярное произведение векторов, звездочка * обозначает комплексное сопряжение. Здесь и далее суммирование предполагается по всем значениям указанной переменной. Решение (3) получается с учетом того, что (rn) = (kn) = 0, или, что то же самое, (1r) =(1k)=0. Очевидно, что (3) на самом деле является решением уравнения ak = r + Ar ,

где A r - погрешность определения координат пятен. Тогда погрешность определения a будет равна

A a = ( k A r )/( kk ) .                                (5)

Угол ф можно найти как ф = arctg( a y / a x ) = arg a = Im(ln a ). Его погрешность в линейном по A a приближении можно найти, как

_{А т} ( A a । a * A a - a A a *

Aq = Im — =-------

I a J      2i a a

.

Подставляя (3) и (5) в (6), с учетом того, что a ^* a = H ², получаем

Aq =

( kr )‘ ( k A r ) - ( kr )( k A r ) ‘ 2i H ² ( kk ) 2

Ограничиваясь первым порядком A r , можем считать, что a k = r , тогда

(kr У (kAr) = a * (kk )* (kAr) = (kk )* (rAr), и, так как (kk)*=(kk), имеем

_A = ^{( r A r )-( r A r} У = ^{( x A} y ^)-( y ^{A x} ) ^ф 2i H ² ( kk )        H ² ( kk ) ’

где x , A x , y , A y - вещественные вектора координат пятен и их погрешностей. Оценим погрешность измеренного угла в предположении отсутствия геометрических искажений, когда все Δ x и Δ y имеют случайный характер с нулевым средним значением. Тогда, предполагая равенство погрешностей по обеим координатам, имеем

| (^A x ) 2J = o 2 =^ ( ^A y ) 2) = ^a 2 = y,

2 _ ⁽ xx ^{) + (} УУ ) _2₌     S ²

’’ 2 H 4 ( kk ) 2    "2 H ² ( kk ) .

При достаточно больших значениях числа пятен знаменатель может быть легко вычислен приближенно. Если считать, что область анализа изображения марки представляет собой круг радиуса R (пикселей), то максимальные центрированные значения номеров пятен равны R / H. Тогда

R / H                  ₄

( kk ) = S ( i n ^{+ j} " ) ~ ^ ( i 2 ^{+ j} 2 ) di ^dj = I r 2 ^{2 П} r ^dr = 2 H 4 ’

H ²

° Ф =^° . π R ⁴

Общее число пятен, используемых для обработки, можно вычислить делением всей площади измеряемой области на площадь одной ячейки сетки N = n R ²/ H² , тогда

H    Vn     a c’ = П№ a = NH a = RTN '

Для камеры с матрицей 5 Мпикс возможный радиус R = 1000, тогда для пятен c шагом H = 15 пикс и СКО координат пятен σ = 0,01 пикс погрешность угла оказывается равной 8,5∙10 ^–8 рад = 0,017".

Если для определения угла поворота использовать всю матрицу камеры размером a × b , то в формуле для погрешности R заменяется на приведенный размер L* :

a 2 b 2

( kk ) = X ( i n + j n ) « J J ( i ² + j ² ) di dj = ab ( a ^4 ^b ) , - a/ 2 - b/ 2                        ¹² H

,      6 H ²      ,      6 a ²                  a              I a ² + b ²

оф =-----------a2 =----------,    оф =---;=, L = .------- ab (a2 + b2)     N (a2 + b2)          L* Nn         \ 6

Для камеры с соотношением сторон кадра 3×4 использование всей площади матрицы вместо вписанного круга уменьшает СКО примерно на 30%.

• 1.2.    Линейные координаты

Линейные координаты марки X , Y определяются через усредненное положение ее элементов

X = ( x ^, a X =a²/ 2 N , Y = yy, , a Y =a²/ 2 N ,

Этот очевидный результат тем не менее показывает, что при СКО координат пятен σ = 0,01 пикс, N = 20000 и размере пикселя 3,5 мкм СКО усредненных координат марки составляет 0,18 нм.

• 1.3.    Период марки

Оценим теперь погрешность периода марки H . Так как

a _X = a Y = a/ 22N .

H ² = a * a =

( kr ) * ( kr ) ( kk )²

A H =

( k A r ) ( kr ) + ( kr ) * ( k A r ) a ( k A r ) + a * ( k A r ) ( r A r ) + ( r A r ) ( x A x ) + ( y A y ) 2 H ( kk )²        =      2 H ( kk )      =    2 H ( kk )    =    H ( kk )

c H

⁽ xx ^{) + (} yy ) _c 2 2 H ² ( kk ) 2

c2 _ H4 c2     _ H2c _ Vnc

2 ( kk ) "  n R ^{4 , C} “~ 4 RR ² " NT

Для рассмотренного примера (σ = 0,01 пикс, N = 20000, 3,5 мкм) СКО усредненного периода марки составляет немыслимые 0,003 нм.

• 1.4.    Координаты элементов

Координаты отдельных элементов марки могут определяться разными способами, в нашем случае мы использовали «центр тяжести» – средневзвешенное значение координат пикселей (^k, nk) с учетом его отсчета (яркости) pk.

x < к >  ( ^ ^ _kp_k ) /P , P _ ^ p k .

kk

Тогда погрешность координат элемента марки

^{A x} X ^d x ^A P k ^_ -1 E ^ k ^A p_k - -1 <^> E ^A P k ^_ -1 E ( ^ k —<^> ) ^A p_k . к s Pk      Pk P к Pk

Если считать флуктуации отсчета для пикселей независимыми, то СКО координаты элемента марки будет определяться СКО отсчета c p . Для большинства камер флуктуация отсчета пропорциональна его величине c p _ a p , и тогда

С2 _ ы E(^ k -<Р>) cP _

Pk

1           £ V      ac2_P2X(^k-<^>) aPk _ —,

С 2 _ ¹ X ( ^ k -<^> ) ² Pk _ const .

Pk

Здесь c ^ - среднеквадратичная ширина элемента марки. Суммарная яркость элемента P в общем случае пропорциональна его площади, то есть квадрату размера, и максимальному значению величины отсчета P _ в p max c 2 . Поэтому

a c2 _----- вp max

,

то есть практически не зависит от размеров марки, а только от свойства матрицы камеры (коэффициент α) и формы изображения элемента марки в относительных координатах (коэффициент β).

Увеличение p max возможно как путем увеличения разрядности АЦП видеокамеры и времени экспозиции, так и путём цифрового накопления кадров. В последнем случае p max пропорционально числу суммируемых кадров N f , а СКО координат элементов марки убывает с ростом числа кадров как

c

x

~

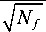
Если же дисперсия отсчета не зависит от его величины c p _ const , то для круглого элемента марки

c2 _P12X(^k-<^>)2cP _2P2X((^k-<^>)2 + (Пk-)2)cP ®4P2-cP

где p - радиус зоны усреднения. И в этом случае P = Y P max пр ² ( у - коэффициент пропорциональности),

c

x

^c P

Пу ² P max

При цифровом накоплении кадров P max и c 2 P растут пропорционально N f , поэтому зависимость (16)

по-прежнему выполняется.

2. Эксперимент

Измерения проводились на трех камерах с CMOS-сенсором, 8-битной глубиной (256 уровней яркости). Параметры камер приведены в табл. 1.

Измерительная марка с периодом 50 мкм и диаметром элементов 30 мкм была изготовлена методом фотолитографии, погрешность координат элементов не превышает 0,5 мкм.

Табл. 1. Параметры видеокамер

Камера	Размер поля, Мпикс	Кадр	Размер пикселя, мкм
A	1,4	1360×1040	5,2
B	5,1	2464×2056	3,45
C	26,2	5120×5120	4,3

2.1. Шумы камеры

Шумовые характеристики различных камер отличаются, зависят от температуры и часто никак не декларируются производителем. Поэтому было произведено независимое исследование шума использованных камер. Для этого использовалось изображение марки, содержащее необходимый диапазон градаций серого. Для каждого пикселя в течение заданного времени вычислялись среднее значение и дисперсия отсчета. Поскольку средние значения прини-

мают произвольное (не целое) значение, результаты затем группировались с привязкой к ближайшему целому значению и вычислялась средняя по всем пикселям с близким отсчетом дисперсия. Количество пикселей, по которым проводилось усреднение, со- ставляло десятки тысяч. Анализ производился как для введенных одиночных кадров, так и для суммы их фиксированного числа (цифрового накопления).

На рис. 2 показана зависимость дисперсии шума D от отсчета p для камеры А и линия тренда.

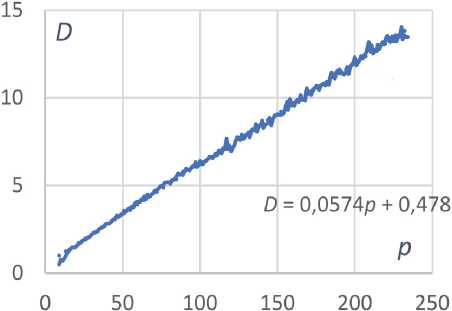
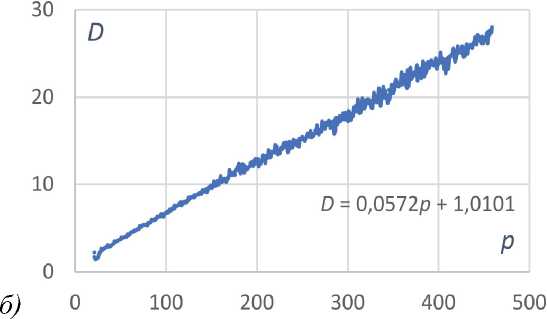
Рис. 2. Дисперсия шума D в зависимости от отсчета p для камеры A для одного (a) и двух (б) накопленных кадров

Видно, что при цифровом накоплении двух кадров дисперсия удваивается, что свидетельствует об отсутствии корреляции и справедливости формулы (16).

Для камеры C (рис. 3) зависимость носит аналогичный характер, но при цифровом накоплении дисперсия растет несколько быстрее, чем сумма диспер- сий, что свидетельствует о наличии корреляции шумов для соседних кадров.

Шумы камеры В (рис. 4) носят принципиально иной характер. Однако и в этом случае цифровое накопление приводит к суммированию дисперсий и справедливости формулы (16).

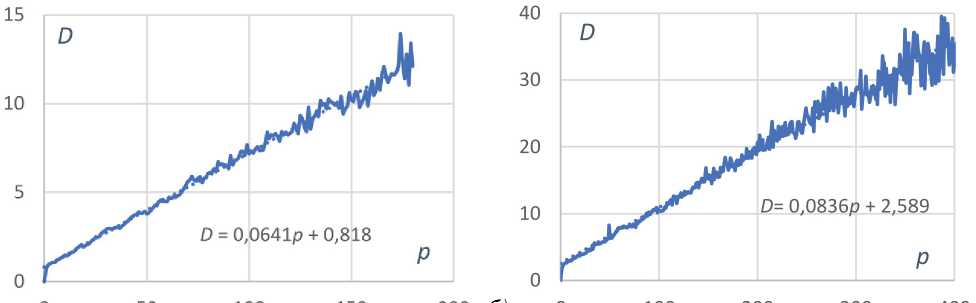
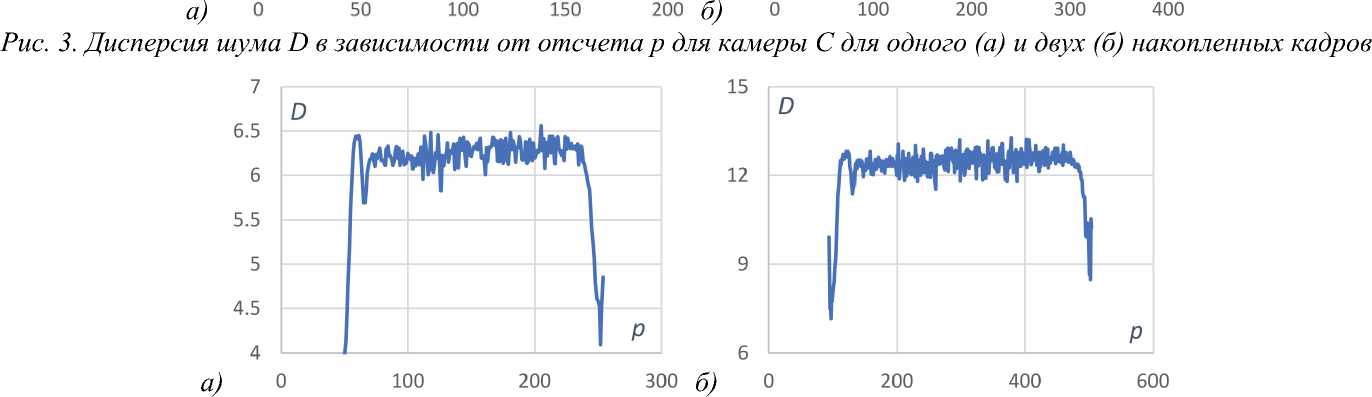
Рис. 4. Дисперсия шума D в зависимости от отсчета p для камеры B для одного (a) и двух (б) накопленных кадров

Полученные зависимости для камер А и С объясняются стохастической природой образования электронно-дырочных пар при попадании фотонов в элементы сенсора. Снимаемый с сенсора сигнал определяется числом поглощенных фотонов с учетом квантовой эффективности. Это случайная величина, дисперсия которой пропорциональна среднему значению.

Отсутствие такой зависимости у камеры В связано со встроенной гамма-коррекцией – сигнал пропорционален квадратному корню из числа поглощенных фотонов. Простейший расчет показывает, что в этом случае дисперсия не зависит от отсчета. Если учесть, что скорректированный отсчет можно записать как pγ = pmax p, то pmax         2    pmax 2 αpmax

σ p _γ=       σ p , σ p _γ=     σ p =        .        (19)

• 2    p            4 p       4

• 2.2.    СКО координат элементов

• 2.3.    Случайная погрешность измерения положения марки

Используя (19), данные рис. 4 и учитывая, что p max = 256, находим α = 0,098. Это значение больше, чем у камер А и С, так как размер пикселя у камеры В значительно меньше.

Определения СКО случайной погрешности координат элементов марки производилось для различных чисел цифрового накопления. Результаты измерений приведены в табл. 2.

Непосредственное измерение СКО также подтверждает зависимость (16). На рис. 5 показаны зависимости ln D от ln N f для камер А и С. Коэффициент линейной регрессии с высокой точностью равен ½.

Таким образом, простое цифровое накопление кадров позволяет существенно уменьшить случайную погрешность измерения.

Высокая разрешающая способность матричной технологии позволяет получить важную измерительную информацию при анализе длительных треков измерений при дестабилизирующем влиянии окружающей среды, включая тепловое воздействие компонентов системы.

Табл. 2. СКО координат элементов для различного количества накопленных кадров N f

N f	СКО камера А, пикс	СКО камера B, пикс	СКО камера C, пикс
1	0,01053	0,01129	0,01287
2	0,00748	0,00813	0,00912
3	0,00609	0,00665	0,00743
5	0,00473	0,00518	0,00575
9	0,00354	0,00387	0,00429
16	0,00266	0,00290	0,00325

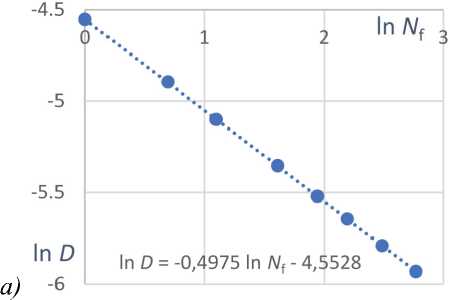
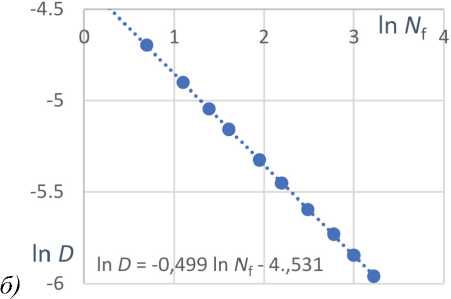
Рис. 5. Зависимость логарифма дисперсии координат элемента D от логарифма количества накопленных кадров N f для камер A(a) и C(б)

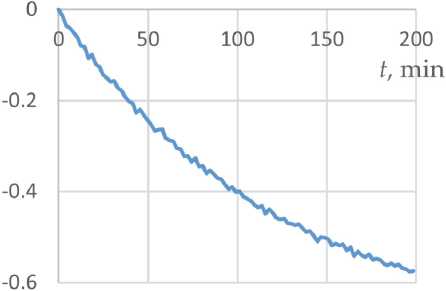
В течение трех и более часов, за которые температура изменялась на несколько градусов, измерялись значения угла поворота, координат и периода неподвижной марки. Их изменения в результате теплового дрейфа описываются гладкими функциями, что позволило исключить тренд и выявить случайную погрешность измерения.

На рисунках ниже показаны зависимость изменения угла (рис. 6), координаты Х (рис. 7) и периода марки от времени (рис. 8) и их отклонение от линии тренда, аппроксимированной дробно-рациональной функцией. Измерения выполнены камерой А с шагом по времени 2 минуты, полное время измерений – 200 минут, перепад температуры за время эксперимента – около 2,5оС.

Каждый отсчет получен усреднением 10 измерений, выполненных с цифровым накоплением 5 кадров. Количество элементов марки, участвующих в обработке, равно 12000; период марки на ее изображении в камере составляет 9,34 пикселя, что соответствует увеличению объектива 0,971х.

Изменение угловой координаты за время эксперимента (рис. 6) составило более 0,5" при разрешающей способности измерений порядка 0,01". СКО измерения угла составляет 0,0047". Применение формулы (9) для СКО элементов марки 0,0047 пикс (табл. 1) с учетом уменьшения погрешности в результате усреднения по 10 отсчетам дает оценку погрешности 0,0048".

а)

б)

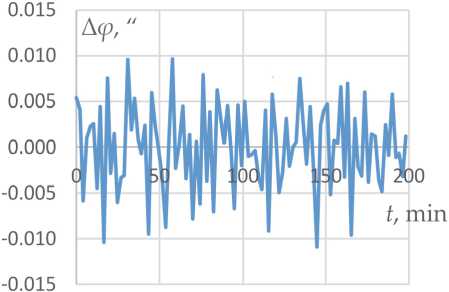
Рис. 6. Изменение угла (a) и его случайные отклонения от линии тренда (б) в зависимости от времени

Изменение координаты центральной (условно) точки марки за время эксперимента (рис. 7) составило 50 нм при разрешающей способности измерений порядка 0,2 нм. СКО измерения координаты Х составляет 0,068 нм, для Y – 0,070 нм. Формула (11) с учетом уменьшения погрешности в результате усреднения по 10 отсчетам дает близкое, но немного меньшее значение 0,050 нм.

Изменение периода элементов марки за время эксперимента (рис. 8) составило доли нм при разрешающей способности измерений менее 0,01 нм. СКО периода составляет 0,0023 нм. Формула (12) с учетом уменьшения погрешности в результате усреднения по 10 отсчетам дает в 2 раза меньшее значение 0,0011 нм.

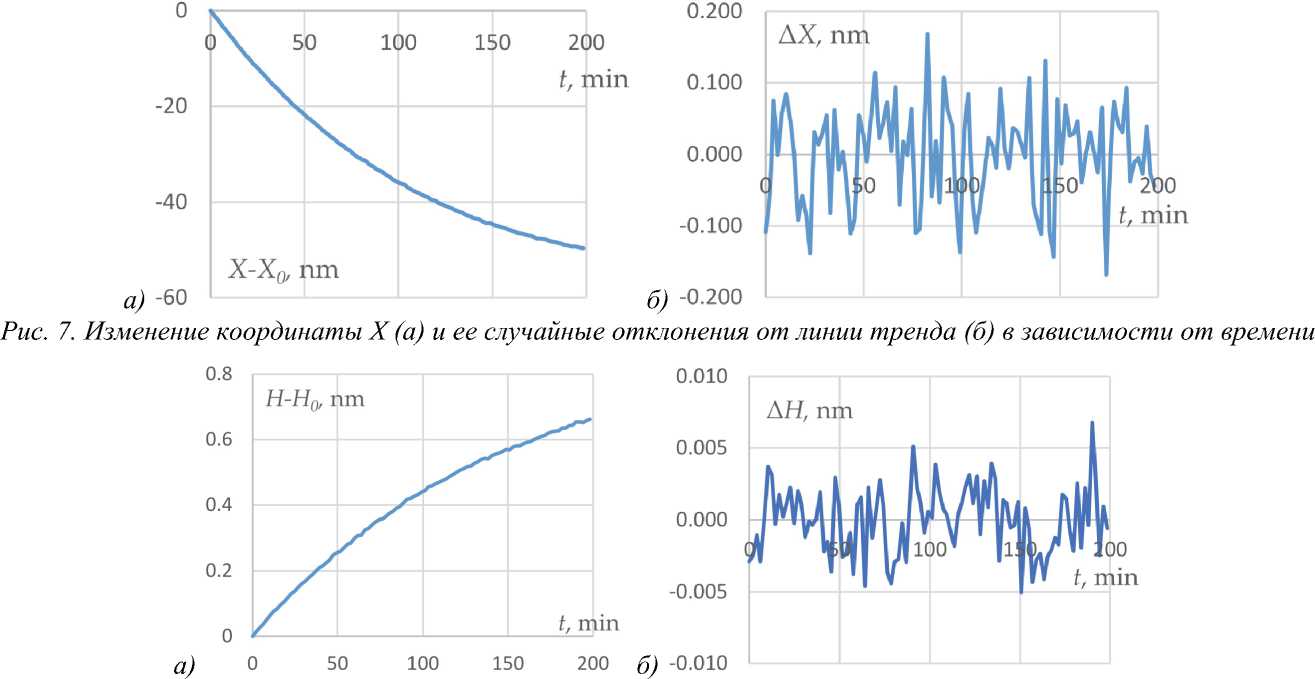
Рис. 8. Изменение периода марки H (a) и его случайные отклонения от линии тренда (б) в зависимости от времени

В табл. 3 приведен фрагмент протокола, содержащий средние значения, рассчитанные по 10 измерениям, и соответствующие СКО. Эти СКО включают в себя не только случайную ошибку, но и дрейф, поэтому они немного больше, чем рассчитано выше.

Все три камеры были протестированы в ходе экспериментов. По времени обработки уменьшалось количество накопленных кадров и измерений. В табл. 4 приведены параметры – период H в пикселях и нано- метрах, количество обработанных элементов марки Ne, количество усредненных измерений Nm и количество накопленных кадров Nf.

В табл. 5 приведены СКО, рассчитанные по экспериментальным данным после вычитания аппроксимации тренда (Эксперимент), и СКО, рассчитанные по формулам (9– 12) и данным табл. 1, 4 (Теория). Оба значения достаточно близки, если иметь в виду простые допущения при выводе формул.

Табл. 3. Фрагмент протокола

№	СКО φ,′′	H , нм	СКО H , нм	X , нм	СКО X , нм	Y , нм	СКО Y , нм
70	0,0015	48623,6417	0,0014	3480121,695	0,057	2735359,498	0,080
71	0,0041	48623,6469	0,0017	3480121,661	0,046	2735359,519	0,074
72	0,0040	48623,6505	0,0024	3480121,903	0,153	2735359,486	0,124
73	0,0034	48623,6516	0,0014	3480121,886	0,082	2735359,648	0,148
74	0,0049	48623,6553	0,0018	3480121,691	0,122	2735359,174	0,091

Табл. 4. Параметры, использованные в экспериментах

Камера	H , пикс	H, нм	N e	N m	N f
A	9,34	48568	12144	10	5
B	14,89	51370	21786	5	3
C	12,20	54900	122253	2	2

Табл. 5. Экспериментальные и теоретические значения СКО угла поворота, координат центра и периода марки

Камера СКО φ,′′ СКО X, нм СКО Y, нм СКО H, нм A Эксперимент 0,0047 0,070 0,12 0,0023 Теория 0,0048 0,050 0,050 0,0011 B Эксперимент 0,0020 0,084 0,057 0,0010 Теория 0,0033 0,049 0,049 0,00084 C Эксперимент 0,0017 0,14 0,11 0,0015 Теория 0,0016 0,082 0,082 0,00042 Измерение динамики величины периода при изменении температуры позволяет выполнить оценочную проверку полученных результатов. Будем считать, что изменение периода связано с температурной деформацией марки, выполненной из стекла. При температурном коэффициенте линейного расширения (ТКЛР) стекла, равном 7^10 –6, изменение периода для номинала 50 мкм при перепаде температуры на 2,5 градуса составит порядка единиц нм, что хорошо совпадает с результатами измерений.

Заключение

Важность полученных оценок случайной погрешности измерений заключается в том, что нам необходимо было показать реальность и достижимость измерений на уровне нанометров. В обычной измерительной системе это кажется невозможным, поскольку ее метрология определяется разрешающей способностью объектива и фотоприемной матрицы, составляющей единицы микрометров. Теоретический анализ и реальные измерения в рамках проведенных исследований подтверждают возможность измерения угловых координат со случайной погрешностью 0,005" и измерения линейных координат со случайной погрешностью менее 0,1 нм. При этом речь идет о минимальной конфигурации матричного измерителя. Еще более удивительная оценка получена для измерения периода элементов марки. Случайная погрешность этих измерений составила тысячные доли нм.

Подчеркнем, что полученные результаты не имеют однозначного отношения к точности. Есть много проблем со стабильной средой, температурой камеры и так далее. С другой стороны, измерения, сделанные в изменяющихся условиях, позволяют надеяться, что наши оценки не являются результатом «измерения одной и той же картины» и показывают реальные возможности матричной технологии.

Отдельную ценность представляют оценки статистики шумов в разных цифровых камерах, позволяющие разделить их на аддитивный и мультипликативный. Они дают реальный критерий для выбора камер для матричных измерителей.

Работа выполнена при финансовой поддержке в рамках гранта РНФ № 20-19-00412.