Матричное решение задачи 4x4 методом Вентцеля - Крамерса - Бриллюэна для плоского неоднородного анизотропного слоя

Планарные структуры различным образом преобразуют амплитуду, фазу, поляризацию, направление распространения света. Поэтому они важны для развития элементной базы нанофотоники. Новые оптические устройства произвели революцию в областях связи, зондирования, обработки и хранения информации благодаря небольшим размерам и низкой стоимости [1]. Варьируя градиент показателя преломления слоя, можно манипулировать светом – его фазой и интенсивностью. Это позволяет создавать GRIN-волноводы с градиентным индексом для конвертации мод [2]. На основе планарных структур реализуются широкополосные светоотражающие тонкоплёночные многослойные аттенюирующие зеркала [3] для спектроскопии, диэлектрические многослойные датчики в геометрии Кречмана на основе волноводных мод [4], альтернативные конструкции в линзах Френеля для построения интегрированных фотоэлектрических систем [5], выполняется дизайн оптических мультиплексоров и демультиплексоров [6], создаются цветные голограммы, зависящие от поляризации света [7]. Для расчётов коэффициентов отражения и пропускания в плоских слоях и векторов полей в волноводах удобны матричные методы; это показано в книге [8] на примере метода характеристических матриц 2×2 для случая изотропной однородной среды. Расчёты полей в многослойных структурах часто выполняют методом передаточной матрицы [4] 2×2. Матричное решение позволяет выполнять «сшивку» граничных условий в наиболее компактной форме. Это удобно как для изотропных, так и для анизотропных слоёв. В общем случае произвольной ориентации плоскости падения волны относительно оптической оси решение для анизотропного слоя имеет вид матрицы 4×4.

Для случая анизотропной стратифицированной среды, представленной в виде набора тонких однородных слоёв, матричное решение 4×4 было пред-

ставлено в статье Тайтлера [9] в 1970 году. Получены матрицы отражения и прохождения для однородного слоя с произвольным тензором диэлектрической проницаемости в случае наклонного падения электромагнитной волны (ЭМВ). Затем, немного позднее, Берреманом был разработан метод дифференциальной матрицы 4×4, предназначенный решить проблему отражения и пропускания холестерическими жидкими кристаллами, а также жидкими кристаллами с непрерывно меняющимся, но плоским упорядочением [10]. Метод Берремана был модифицирован в работе [11], где был предложен новый подход к изучению оптических свойств анизотропных стратифицированных сред. Метод состоит в нахождении нового базиса для матрицы 4×4, в которой конкретная задача записывается и рассчитывается более удобным способом. Для записи решения применялся базис из волн правой и левой поляризации, распространяющихся в прямом и обратном направлении; подробно изучен случай распространения света в холестерических и кираль-ных смектических жидких кристаллах при малых углах падения. Способность нематических и холестерических жидких кристаллов (ЖК) менять ориентацию молекул при воздействии внешних полей находит множество приложений: они применяются в качестве датчиков температуры [12], электрических и магнитных полей, а также в ЖК-мониторах. На эффектах кручения основана работа нормальной белой (NW) и нормальной чёрной (NB) ячеек [13]. Для дизайна новых устройств на основе ЖК необходим математический аппарат, описывающий процесс распространения волн в среде с учётом неоднородности и анизотропии.

Для управления поляризацией и интенсивностью света, помимо жидких кристаллов, в настоящее время созданы полимерные двулучепреломляющие материалы, а на их основе – оптические элементы с новым свойством: осевым градиентом двулучепреломления [14]. О разработке новых фотонных метаматериалов из пространственно-периодических, сильно двоякопре-ломляющих диэлектриков идёт речь в работе [15], численный анализ предложенных анизотропных фотонных кристаллов предполагает чрезвычайный рост амплитуды поля в пределах структур на фотонных резонансах полосы пропускания.

Для расчёта планарных неоднородных структур часто применяется модель слоистой среды, когда материал с непрерывно изменяющимися вдоль одной координаты свойствами рассматривается как набор однородных слоёв. Если применить такой подход, например, к анизотропной среде с кручением, то в задаче появляются искусственные разрывы значений компонент тензора диэлектрической проницаемости на границах, которых в реальности не существует. Тогда в расчётах неизбежно будет учитываться отражение от границ слоёв, которых в реальном объекте нет. Кроме того, в неоднородной анизотропной среде при распространении волны в каждой точке меняется её волновой вектор, а в модели слоистой среды это изменение сводится к набору дискретных направлений. Этих недостатков лишён метод Вентцеля – Крамерса – Бриллюэна (ВКБ) [16]. Данный метод был применён к планарным отражающим структурам в работе [17]. Использованы новые пробные решения ВКБ и в виде функций Эйри, они позволяют очень точно рассчитать фазовые сдвиги в точках поворота, что позволяет находить почти точные собственные значения для волноводов. В работе [18] было представлено матричное ВКБ-решение для ЭМВ, отражённой неоднородной изотропной реагирующей средой. Решение для анизотропной среды получено в работе [19], в ней рассматривается случай, когда оптическая ось лежит в плоскости падения. Матричное ВКБ-решение применялось нами для расчёта режимов анизотропного неоднородного планарного волновода. Для неоднородного анизотропного планарного волновода с непрерывно изменяющимися свойствами оно применялось работе [20]; для анизотропной неоднородной среды с изменением направления оптической оси в слое – в работе [21]. Различные способы решения задачи 4×4 для анизотропных и бианизотроп-ных планарных структур представлены в работах российских учёных [22–23]. В настоящей работе предлагается матричный математический аппарат для расчёта полей в анизотропных неоднородных планарных структурах с кручением (современных искусственных анизотропных метаматериалах, холестерических жидких кристаллах, где ориентация молекул изменяется при удалении от границы слоя), а также для расчёта матриц отражения. Матричное решение получено методом Вентцеля – Крамерса –Бриллюэна; в отличие от широко распространённых матричных методов полученное решение предназначено для оптических анизотропных структур, оптические свойства которых являются непрерывными функциями поперечной координаты. Такие устройства могут не только менять поляризацию света, но также служить оптическими переключателями: получать из волны s-поляризации волну p-поляризации и наоборот.

1. Основные уравнения

Рассмотрим наклонное падение плоской ЭМВ на анизотропный одноосный неоднородный слой толщиной d , показанный на рис. 1. Оптическая ось среды не лежит в плоскости падения.

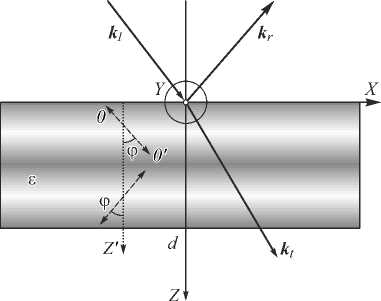
Рис. 1. Плоскость падения ЭМВ на анизотропный неоднородный слой с переменным направлением оптической оси 00’

Оптическая ось при удалении от границы раздела «1–2» меняет внутри неоднородной среды своё направление. Она ориентирована под постоянным углом φ к оси 0 Z и вращается вокруг неё при изменении z , как, например, в холестерическом жидком кристалле. Угол х поворота оптической оси относительно оси O Z является функцией координаты z и имеет вид: х = Х 0 + k z . В этом случае все компоненты тензора диэлектрической проницаемости среды будут отличны от нуля, кроме отдельных положений z 0 , когда х ( z 0 ) = m п .

Из уравнений Максвелла для роторов полей E и H в декартовых координатах и из материальных уравнений анизотропной среды следует система обыкновенных дифференциальных уравнений (ОДУ):

( Е Л

Y

A H x d z H Y

I Ex J

(      0

ik 0

^аб 22 ^a ^^^^^^^^^^^^^^^^^^^^^^^^^_ ^^^^^^* ^^^^^^^^^^^^^^^^^_

^Б 33 Ц 33

^Аб 12

^Б 33

^Б 33

-p    0

0    а^Б 2 ³

^Б 33

0     ^аБ 1з

^Б 33

0 '

^АБ 21

^Б 33

х

^АБ 11

^Б 33

аБ 1з

^Б 33

Г Е Л

Y

X

HX

H Y

I Ex )

Все коэффициенты б^ - функции координаты z .

^Л£ 11 = ^£ 11 ^£ 33

^Ле 22 = ^£ 22 ^£ 33

^Ле 21 = ^£ 21 ^£ 33

Л£ ₁₂ = £ ₁₂ £ ₃₃

^£ 13 ^£ 31 ,

^£ 2з ^£ з2 ,

^£ 23 ^£ 31 ,

^£ 13 ^£ 32 ,

а = n ( z ) ■ sin 9 ( z ),

(2a) (2b) (2c) (2d)

(2e)

V = — bc + v, G = d2 — ef + w.

(7c)

(7d)

Для нахождения системы решений для (1) мы воспользовались базисными функциями:

согласно закону Снеллиуса, а =const. Математически данная задача сводится к системе из четырёх обыкновенных дифференциальных уравнений с переменными коэффициентами вида:

z ik0 jM^

F_j ( z ) e ⁰

.

—*

d Q = ik ₀ . A ( z ) Q .

Здесь Q = ( E y H x H y E x ) T . Рассмотрим случай, когда тензор £ симметричен, а его компоненты медленно меняются на расстоянии порядка длины волны излучения. Матрицу системы (1) запишем в виде:

( 0

71( z ) =

2. Матричное решение

Для решения методом ВКБ [14], когда проекции полей пропорциональны экспонентам exp[ ik ₀ g ( z )], где c ( z ) представляется в виде ряда:

( \ Г \ ^G 1 ( z ) ^G 2 ( z )

G⁽ z ) = O 0 ⁽ z ) + -7— + "—Г ⁺ ..., i^k 0       ⁽ ik 0 )

функции (8) являются начальным приближением. Это значит, что интегралы в формуле (8) имеют вид:

z

lMk)dk n Iz).

С помощью функций (8) запишем проекции полей Hx и Ex :

— b

0 ' h

p d

c h

—i

—

к^— p

e d

.

Все элементы матрицы A ^ˆ ( z ) в формулах (1 –4) могут быть функциями координаты z . Из характеристического уравнения системы ОДУ (1) det (A — X I)=0 получаем её собственные значения:

x

ik 0 j X 1 ( k ) d k            ik 0 j X 2 ( k ) d k

= S 1 e  ⁰        + S ₂ e  ⁰       ,

zz ik0 jX3 (k) dk           ik0 j X4 (k)dk

E x = S ₃ e  ⁰       + S ₄ e  ⁰

.

^X 1,2 =

2 uu

--±3 b ■ c + —

— v ,

(5a)

^X 3,4 =

2 u e ■ f—w + — — u ■ d.

(5b)

Величины u , v , w найдены таким образом, чтобы привести характеристическое уравнение четвёртой степени для системы ОДУ (1) к уравнению вида:

(X2 + U X+ V) (X 2 + F X+G) = 0, или к двум уравнениям второй степени. Здесь использованы следующие подстановки:

U = u ,

F = — d — u ,

(6) были

(7a)

(7b)

Y ( z ) =

z

S ^ik 0 j ^X 1 (^k) ^{d k}

—nf A e •

z ik0 jX1 (k) dk

S 1 e ⁰

z

S     ^ik 1 j ^X 2 (^k) ^{d k}

П 1 f -2 e ⁰

A

z ik0 j X2 (k)dk

S ₂ e  ⁰

—

к

z

S     ik 0 j X 1 ( k ) d k

P П 1 _A e ⁰

S ik 0 j X 2 ( k ) d k —П 1 p "Л e °

Фундаментальная матрица решения (ФМР) системы (1) для анизотропного неоднородного слоя получается методом Вентцеля – Крамерса – Бриллюэна, при этом использовался подход, представленный в книге В. Вазова [24]:

Y (z ) = Gt (z )■ diag e

ik 0 j X 1 ( k ) d k 0

,...,

ik 0 j X 4 ( k ) d k e ⁰

. (11)

G ^ˆ ( z ) – матрица с коэффициентами, зависящими от z ; причём G ^ˆ ( z ) удовлетворяет системе (1). Чтобы найти ФМР, подставим решения для проекций H x и E x в систему ОДУ (1). Таким способом мы нашли ещё две проекции векторов полей и можем записать ФМР Y ^ˆ( z ):

S

"Л (n 2p +

z ik0 jX3 (k) dk hf) e 0

St(П 2 P — hf )

z ik0 j X4 (9 dk e 0

S                      ik 0 j X 3 ( k ) d k

"A³- ( hp + n ₂ c ) e ⁰

z ik0 jX3 (k) dk

S ₃ e ⁰

S                       ik 0 j X 4 ( k ) d k

"A4- (hp — П 2 c) e 0

ik 0 j X 4 ( k ) d k

S 4 e ⁰

.

Здесь А = f - c - p 2 . Матрица Коши рассчитывается по стандартной формуле:

N ( z ,0 ) = Y ( z ) Y ^{- 1} ( 0 ) .                           (13)

Формулы (9) и (10) представляют собой начальное приближение метода ВКБ; после их подстановки в систему (1) мы получили множители при экспонентах у проекций H x и E x , которые удовлетворяют уравнениям системы. Решениями системы (1) являются четыре базисные волны, которые определяются свойствами среды при данном значении z . Поляризация базисных волн зависит от направления оптической оси в среде и от угла падения. Решение задачи выполнено методом ВКБ и представлено в виде матрицы Коши 4×4, описывающей изменение проекций полей электромагнитной волны при её распространении в среде.

С помощью матрицы Коши получены матрицы амплитудных коэффициентов отражения и пропускания волн произвольной поляризации для неоднородной анизотропной плоской среды. В качестве базиса для падающей волны можно выбрать волны s- и p-поляризации, волны правой и левой круговой поляризации или волны двух ортогональных эллиптических поляризаций. Мы будем описывать падающие и отраженные волны с помощью s- и p-поляризаций. Данный метод применен для расчёта матричных коэффициентов отражения слоя со спиральным изменением направления оптической оси.

Из условий непрерывности тангенциальных составляющих полей E и H следует система, связывающая s- и p-компоненты падающей и отражённой волн:

" P n ( n ii + P i n 12 ) " ( n 21 + P i n 22 )       лК ( P n ( n i3 + Q i n i4 ) " ( n 23 + q i n 24 ))Y E s, -I =

_VF ( qn ( n 31 + P l n 32 ) — ( n 41 + P l n 42 ) ) FF ( qn ( n 33 + q i n 34 ) — ( n 43 + q i n 44 ) ) ) I ^E P¹ ) J ^- ( P n ( n ii — P i n i2 ) " ( n 2i — P i n 22 ) )      "VY( P n ( n i3 ^- q i n i4 ) " ( n 23 "  q i n 24 ) ) If E sr

cF ( q n ( n 3i "  P i n 32 ) ⁺ ( n 4i "  P i n 42 ) )  Y% ( q n ( n 33 ^- q i n 34 ) "  ( n 43 "  q i n 44 ) ) J I E r

Или, кратко:

s 11

s 21

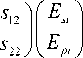
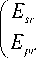
Из этого следует, что матрица отражения для волн

Были рассчитаны зависимости модулей коэффициентов матрицы отражения | R sp | и | R ps | от угла падения света 9 i для различных значений угла кручения Ах оптической оси в среде, указанных выше.

s- и p - поляризации имеет вид:

^

R =

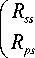
^RSP I V-'C p 1 = X S . R pp

3. Расчёт матрицы отражения

Для анизотропной среды, s o =2, s e =2,4, d=5 X 0 , выполнен расчёт модулей амплитудных коэффициентов матрицы отражения (16). Среда 1 – воздух, подложка – вода. Угол между оптической осью (ОО) и нормалью 0 Z , проведённой к границе раздела сред «1–2», составляет ф = 45°. Первоначально в плоскости z = 0 оптическая ось параллельна плоскости падения: х (0) = 0. Затем в слое изменяется направление оптической оси на угол А/ . Величина кручения среды А/ принимала в расчётах следующие значения: 0°, 45°, 90°, 135° и 180°.

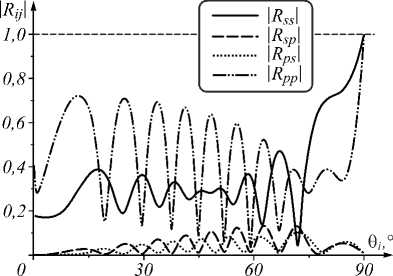
Рис. 2. Угловые зависимости модулей амплитудных коэффициентов матрицы отражения It при ф =45° и угле кручения Д% =90°

Рис. 3. Угловые зависимости |R s _P| при ф =45° и угле кручения Л% , принимающем значения, указанные на рисунке

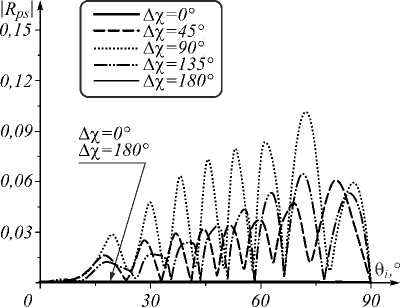
Рис. 4. Угловые зависимости |R_P s | при ф =45° и угле кручения Л% , принимающем значения, указанные на рисунке

Расчёт показал, что при начальном угле χ =0, когда оптическая ось на границе раздела сред лежит в плоскости падения, максимальные абсолютные значения амплитудных коэффициентов R sp , R ps достигаются при угле кручения Δχ = π /2. Если Δχ = π , или Δχ =0, то значения u , v и w , определяемые формулами (7), будут равны нулю, а коэффициенты R sp и R ps также принимают нулевые значения. То есть при отсутствии кручения или при кручении, равном π , кросс-поляризации при отражении волны не происходит. И, наоборот, кросс-поляризация волн s- и p-поляризации будет наибольшей при угле кручения, равном 90°.

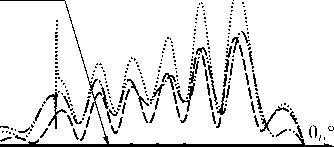
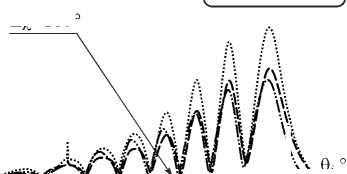
Расчёт матриц отражения при изменении угла кручения Δχ выполнялся также для случая, когда угол ϕ между оптической осью и 0 Z составлял 15°. Результаты расчётов представлены на рис. 5, 6 и 7. Из рис. 5 видно, что угловые спектры модулей коэффициентов |R ss | и |R pp | имеют особенности в виде скачков. На рис. 6 и 7 можно видеть, что |R sp | и |R ps | имеют аналогичные особенности. Такой результат получен для случая, когда угол преломления θ обыкновенной волны в среде становится равным углу ϕ , тогда преломлённая волна, возникающая в неоднородной среде на границе раздела z =0, начнёт своё распространение в среде вдоль оптической оси и первоначально будет обыкновенной. Затем, при удалении от границы, направление оси в среде изменяется, волна преломляется и разделяется на обыкновен-

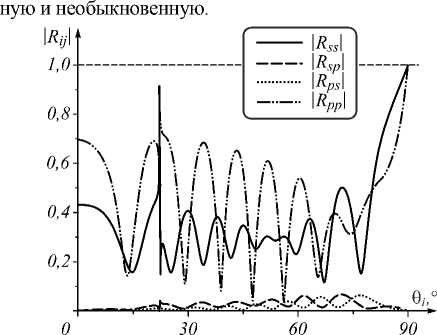
Рис. 5. Угловые зависимости модулей амплитудных коэффициентов матрицы отражения R^̂ при ϕ =15° и угле кручения Δχ =90°

1^1

0,100-

0,075-

----Д/=0°

----^X=45°

............Д7=Р0°

------^=135°

----^=180°

0,050-

0,025-

0            30          60          90

Рис. 6. Угловые зависимости |R_sp| при ϕ =15° и угле кручения Δχ

1^1-

0,100"

0,075-

---АХ=0°

----^X=45O

.........Д7=Р0°

------Дх=735°

---NX=180°

NX=O° NX=18O°

0,050

0.025

V

0            30          60          90

Рис. 7. Угловые зависимости |R_ps| при ϕ =15° и угле кручения Δχ

В этом случае, когда угол ϕ =15° , параметры u , v и w в выражениях (5 а ) и (5 b ) принимают меньшие значения, чем в предыдущем, когда угол между ОО и 0 Z составляет 45° . Обмен энергией между волнами s- и p-поляризации в анизотропной среде при меньшем угле φ будет менее заметным, и коэффициенты R sp и R ps будут меньше по модулю. Для сравнения: если угол между оптической осью и направлением 0 Z выбрать равным ϕ =0° , то кросс-поляризованные компоненты R sp и R ps будут равны нулю и в среде будут независимо распространяться волны s- и p-поляризации. Таким образом, рост угла ϕ между оптической осью и нормалью к границе слоя ведёт к увеличению кроссполяризации.

Полученный матричный аппарат предполагается применять для расчёта устройств обработки оптических сигналов на основе ЖК и анизотропных фотонных кристаллов, переключателей поляризации света.

Заключение

Получен математический аппарат в виде матрицы Коши 4×4 для расчёта полей в планарных анизотропных градиентных структурах с произвольным направлением оптической оси относительно плоскости падения, а также для сред с кручением, учитывающий взаимодействие волн ортогональных поляризаций в среде.

Выполнен расчёт угловых спектров абсолютных значений амплитудных коэффициентов матриц отражения для среды с кручением. Показана зависимость кросс-поляризованных компонент при отражении света от полного угла кручения среды и от угла между оптической осью и нормалью к плоскости слоя.

Полученный матричный аппарат предполагается применять для обработки оптических сигналов, переключателей поляризации света.