МАВ-декодер сигналов ТРКМ с использованием двунаправленного выравнивания

Предлагаемый МАВ-декодер предназначен для работы в составе итеративного турбо-декодера ТРКМ-последовательности. Предполагается, что на передающей стороне турбо-кодер формирует последовательность кодовых символов, представляющую собой объединение двух прореженных последовательностей кодовых вектор-символов, формируемых двумя (верхним и нижним) RSC-кодерами [1]. При этом кодовые вектор-символы представляют собой конкатенацию информационного (систематического) вектор-символа d(/) и проверочного (паритетного) вектор-символа р^, , то есть с^ ^d^p^ J . На приемной стороне выход канала с МСИ подключен к многомерному адаптивному согласованному фильтру, который формирует последовательность достаточных статистик у . Данная последовательность подвергается процедуре двунаправленного выравнивания [2], в результате чего формируются две последовательности отсчетов X И X, на основе которых осуществляется процедура МАВ-декодирования.

Необходимо отметить, что последовательность X формируется прямым выравнивающим фильтром (т.е. выравнивающим последовательность у в прямом направлении) – ПВФ, а последовательность X формируется обратным выравнивающим фильтром – ОВФ. Первый из выравнивающих фильтров подавляет преддейс-твия, а второй – последействия сигнальных элементов принимаемой последовательности на основе критерия минимума среднеквадратического отклонения (СКО).

Рассматриваемый МАВ-декодер предназначен для обработки сигнальных последовательностей, поступающих из канала непосредственно (без перемежения). При этом следует учесть, что сигнальные элементы (СЭ) с нечетными номерами, определяемые кодовыми вектор-символами С2/-1 — С2/-1 ’ формируемыми верхним RSC-кодером, связаны между собой его кодовой связью.

Что касается четных СЭ, то соответствующие им информационные вектор-символы совпадают с прореженными информационными ве к тор-сим-волами верхнего RSC-кодера: d^(2/)=d^(2/), при этом соответствующие проверочные вектор-сим-волы р могут иметь произвольное значение.

Процедура декодирования

На первом этапе задачей МАВ-декодера является вычисление на основе последовательности отсчетов X с выхода ПВФ прямых вероятностных метрик (апостериорных вероятностей) состояний кодовой решетки Ct^/+Ij (где / е О, А -1 – номер шага по кодовой решетке, seO;S-l – номер состояния кодера, L – длина сигнальной последовательности, S – число состояний кодовой решетки), а также вычисление прямых вероятностных метрик (апостериорных вероятностей) ребер ТТЛ                        v(')   /                           7 ы кодовой решетки 1 ^ (в данном случае определяют исходное состояние для заданного ребра г, а I +1 и 5(М определяют его конечное состояние) и функций правдоподобия Aj?) указанных ребер кодовой решетки.

Прямые вероятностные метрики состояний кодовой решетки И (И) определяются как сумма вероятностей всех возможных путей по кодовой решетке, входящих в данное состояние . В

свою очередь, вероятность каждого из указанных

путей определяется как произведение апостери орной вероятности 7 ребра с номером г , ко-

1                                           (7+1)

торое на шаге / входит в состояние S , и веро-

ятности исходного состояния для данного ребра

Т1Т ТТТТТ/Л Т Т Т Т Т Т             ТГТ Т ТТЛ        Т

ОС ^/+Q , вычисленной на предыдущем шаге:

= Z й,л'>-^^м’ w где ^(/) определяет число ребер, входящих в каждое состояние 5 или выходящих из каждого состояния на шаге Знак говорит о том, что указанные апостериорные вероятности ребер получены при использовании ОСР по кодовой решетке. Необходимо отметить, что величина ^(7) на четных и нечетных шагах декодирования может принимать различные значения.

На нечетном шаге в каждое состояние входят 2 ребер, причем каждое ребро кодовой решетчатой диаграммы определяется одним из конечных состояний для заданного ребра Г (исходным s^ (7+1)л или последующим $;. '), а также соответствующим данному ребру информационным (систематическим) вектор-символом d<2/-n, с которым однозначно связан проверочный (паритетный) вектор-символ р; •

На четном шаге декодирования, в силу особенностей кодирующего устройства, каждому из ребер решетчатой диаграммы может соответствовать сигнальная амплитуда, определяемая теми же самыми, что и для верхнего RSC-кодера, к информационными битами, образующими информационный вектор-символ d^(2/*, но с различными возможными вариантами п-к паритетных (проверочных) битов, которые образуют проверочный вектор-символ Р .

J7) ДЛ

Вероятностные метрики ребер Y,-.,!™) =Y., i'>.,., входящие в соотношение (1), представляют собой апостериорные вероятности соответствующего ребра с номером 7" , входящего в состояние _s(^/+l) (или выходящего из состояния S^ ):

(')         o(7)

= App j r^

X

^Appido

o(7)

i , (2)

которые определяются по формулам Байеса, причем на нечетных шагах декодирования, в силу

приведенных выше рассуждений, они однозначно определяются систематическими вектор-сим-волами d1'*:

а на четных шагах указанные вероятности определяются как систематическими d(/), так и пари тетными вектор-символами p :

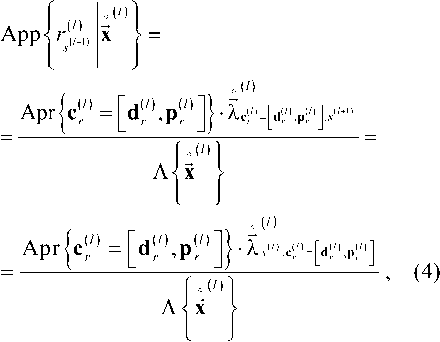
где символ Apr обозначает априорную вероятность, а символ [’] – объединение массивов.

В соотношения (3)-(4) также входит вектор сигнальных отсчетов, вычисленных с учетом действия ОСР по кодовой решетке, соответствующих всем возможным исходным состояниям кодовой решетки, который определяется следующим образом:

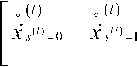
Его безусловная функция правдоподобия определяется по формуле полной вероят ности путем суммирования по всем возможным вариантам ребер кодовой решетки на шаге /:

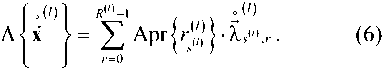
Таким образом, усреднение в (6) осуществляется по всем возможным вариантам ребер кодовой решетки, выходящих из всех возможных состоя-J/)

ний , то есть значения апостериорных вероятностей всех ребер решетчатой диаграммы на шаге выравниваются друг относительно друга.

Рассмотрим теперь процедуру вычисления

A)

функций правдоподобия ребер X_s»'.r = A,-,.v<^/+l> , которые входят в соотношения (3)-6).

Особенностью предлагаемого МАВ-декодера является использование обратной связи по кодовой решетке [2]. С учетом ее действия сигнальные отсчеты, соответствующие каждому из ребер, (7+1)

входящих в состояние s , определяются как

=^' -E6 fc) Л’ (7)

"                      <7=1            x           ’ где X^ - отсчет, соответствующий СЭ с номером / на выходе ПВФ, ^6/ – отсчеты отклика ПВФ на единичный СЭ, Q – память канала связи. При использовании ОСР по кодовой решетке каждому ребру с номером r , входящему в состояние S(,+I), соответствует своя последовательность оценок амплитуд b ,-A" ’ которая определяется путями, входящими в исходное состояние ^^ Д'+i) ■ Иными словами, для каждого исходного состояния формируется свой регистр обратной связи.

Каждый сигнальный отсчет X¹'* с выхода ПВФ включает в себя полезную составляющую b^^b ■ ^0, составляющую, обусловленную МСИ У,ь"-'ЛЛ а также шумовую составляющую v^b^ :

^-b"'.^^"-"^^"'.   (8)

Из соотношений (7)-(8) следует, что значение отсчета принимаемой смеси, соответствующее ребру с номером r , с учетом действия ОСР по кодовой решетке, определяется следующим образом:

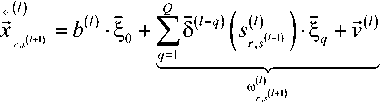
где 6^,'"’^,(A-"‘H^,'’A"'*ⁱ(^sA") представляют собой величины остаточных сигнальных амплитуд, обусловленных погрешностями в цепи ОСР. Два последних слагаемых в (9) образуют совокупную аддитивную помеху ® . .(/+!) D которая, с одной стороны, обусловлена остаточной МСИ, а с другой стороны – шумовой составляющей V^' на выходе ПВФ.

Второе слагаемое в соотношении (9) представляет собой сумму случайных величин с ограниченными дисперсиями. Если предположить, что разностные амплитуды 6(/ ^, обусловленные погрешностью в цепи ОСР, статистически независимы, то ко второму слагаемому в (9) можно применить гауссовскую аппроксимацию. Таким образом, отсчет совокупной аддитивной помехи ®r,s(/+l) представляет собой сумму двух статистически независимых гауссовских случайных величин.

С учетом приведенных рассуждений функции правдоподобия ребер ^^ \/+1) — ^ (/) однозначно определяются как соответствующие условные функции распределения:

J/) Х,т,

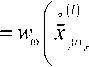
Ь^

d(/',p!')

_ 1

у ^^а

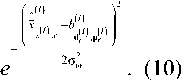
где величина -^j'+i) , определяющая верхний предел суммирования, на нечетных шагах декодирования равна числу вариантов систематических вектор-символов d^(/+ij • -^^(/+i) ^— 2 . На четных шагах декодирования усреднение в соотношении (11) осуществляется по всем возможным вариантам как информационных вектор-символов ^ jL) ’ так и проверочных вектор-символов P_s(/+l) 9 то есть ^_$('+!) ^— 2 •

Для формирования регистра обратной связи состояния s задачей декодера после определения величины bj.h является принятие решения относительно предшествующего состояния по правилу максимума апостериорной вероятности:

где

Необходимо отметить, что значения функций правдоподобия одинаковых ребер, выходящие из различных состояний, отличаются друг от друга, поскольку различным исходным состояниям соответствуют различные регистры обратной связи и, следовательно, различные реализации остаточной межсимвольной помехи.

Рассмотрим теперь процедуру формирования оценок амплитуд СЭ Г"^.....) для цепи ОСР по кодовой решетке, которые входят в соотношение. При этом следует учесть, что применительно к состоянию S все возможные входящие пути образуют полную группу событий, а их апостериорные вероятности зависят как от прямых апостериорных вероятностей ребер Y,.,-(/+,), так и от прямых вероятностей соответствующих исходных состояний ® .+|> ’ вычисленных на предыдущем шаге.

При использовании мягкой (правильнее сказать: усредненной) обратной связи по решению значение оценки амплитуды для конкретного состояния s представляет собой аналоговую величину, а минимум ее среднеквадратического отклонения от истинного значения достигается тогда, когда эта оценка определяются как апостериорное среднее по всем вариантам путей, входящих в состояние 5 ' [3]. На нечетных шагах декодирования эта оценка определяется следующим образом:

?(/) _„G)

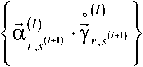
Регистр обратной связи по ветствующий состоянию u-u

b (s(,) 1 =

uralJJ'+l|

rGO;^-l.

решению, соот-

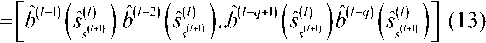
передается состоянию s и модифицируется следующим образом:

b (»^(,) 1 =

[ДД »IH1

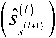
^('-?+2)

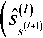
(^(^’^.(W)

Обратные (то есть вычисленные при декодировании по кодовой решетке в обратном направлении) вероятности каждого состояния P^ , апостериорные вероятности ребер yv(/) и оценки сигнальных амплитуд для цепи обратной связи вычисляются аналогично тому, как это делалось при декодировании в прямом направлении. Разница состоит в том, что при их вычислении используется вектор отсчетов X с выхода ОВФ, полученный при выравнивании сигнального пакета в обратном направлении.

В результате приведенных вычислений в процессе декодирования при прямом и обратном проходах формируются соответствующие матрицы вероятностей состояний сигнального пакета:

_         / 7       ,(/и) Тм(/ ) . .(^О bi'l'> = ^n =                           (11)

’                        ДД

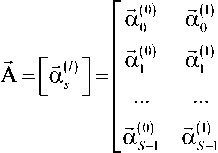
a

a

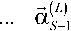
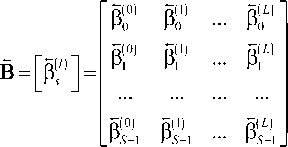
где L – длина сигнального пакета, S – число состояний кодовой решетки.

Наряду с матрицами А и В в процессе их вычисления определяются соответствующие матрицы апостериорных вероятностей всех возможных ребер кодовой решетки

Г = [^]иГ = [у^],         (17)

а также соответствующие матрицы функций правдоподобия

А = [Х«];Л = [Х«],            (18)

где матрицы Г и Л получены в процессе декодирования в прямом направлении, а матрицы Г и Л получены при декодировании в обратном направлении.

Используя матрицы А и Г, а также В и Г, можно получить вспомогательные решения относительно информационных вектор-символов:

-М d

= arg max

■ УаУуИ -аМ И'Н

>;re0;2z-1,(19)

-(/) d

=arg max

. V gW -^

K(/+i) A(/+i).,-?(/+l)=0

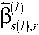
>;re0;2*-l, (20)

полученные, соответственно, при декодировании в прямом и обратном направлениях. Решения (19)(20) могут быть использованы для сравнительного анализа характеристик качества декодера на различных этапах итеративного декодирования.

На рис. 1. приведены вероятностные характеристики вспомогательных решений (19)-(20), полученные методом имитационного моделирования для однолучевого канала связи при удельной скорости модуляции v = 4 Бод/Гц, полученные для ТРКМ-последовательности при использовании кода RSC (7,5) и сигнальной системы ФМ-4. На этом же рисунке приведена вероятностная кривая совпадающих ошибок при декодировании конкретного сигнального пакета (в статистическом смысле вероятностные характеристики решений (19)-(20) совпадают). Из анализа представленных кривых можно сделать вывод о том, что при совместном использовании вероятностных метрик, полученных при декодировании в прямом и обратном направлениях, декодер имеет хорошие потенциальные возможности для улучшения качества указанных решений.

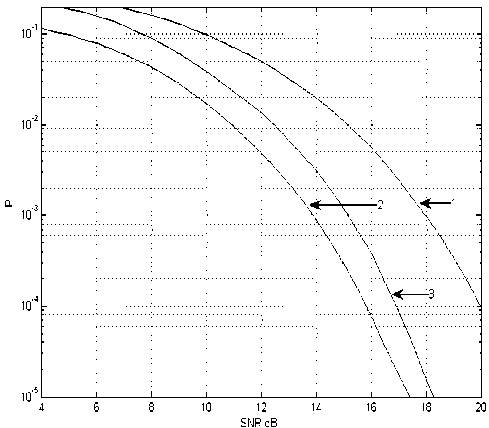
Рис. 1. Вероятностные характеристики МАВ-декоде-ра на различных этапах декодирования: 1 – вероятностные характеристики вспомогательных решений по правилам (20) и (21); 2 – вероятностная кривая совпадающих решений; 3 – вероятностная характеристика МАВ-декодера

Если не учитывать корреляцию между соответствующими отсчетами совокупной аддитивной помехи, введенной в соотношении (9), при декодировании в прямом и обратном направлениях, то, используя матрицы функций правдоподобия ребер Л и A, можно получить результирующую матрицу A (матрицу совместных функций правдоподобия ребер), элементы которой определяются как произведение соответствующих элементов матриц Л и A:

A = [Z"] = PS’^]- (21)

На основе результирующей матрицы правдоподобия A можно сформировать результирующую матрицу апостериорных вероятностей ребер Г , а также матрицы апостериорных вероятностей состояний

А = [а<7(Г)];В = [р<,)(Г)]

Отметим, что при формировании матриц A иВ, определяемых соотношением (23), обратная связь по кодовой решетке не используется, вычисления осуществляются как для обычного символьного МАВ-декодера, подобно тому, как это показано в [1]. На основе матриц А,В и Г можно осуществить принятие жестких решений относительно информационных вектор-символов согласно правилу максимума апостериорной вероятности:

d = arg max <

У            •R(/+l)-

^(Z) M/)../ Pv(/)../’

где j – номер варианта систематического вектор-символа на шаге I .

На рис. 1 кривая 3 характеризует помехоустойчивость принятия решения в соответствии с правилом при наличии сильно выраженной МСИ. Из сопоставления с кривой 1, которая соответствует процедуре декодирования с ОСР по кодовой решетке в одном из направлений (прямом или обратном) на первом шаге итерации, следует, что декодирование по правилу (23) позволяет несколько улучшить помехоустойчивость по сравнению со случаем декодирования в одном направлении.