Мажорирующая оценка коэффициентов ослабления уровней побочных электромагнитных излучений технических средств

П рогнозирование на границе контролируемой зоны (КЗ) уровней напряженности электрического и магнитного полей, возникающих при работе технических средств (ТС), обрабатывающих информацию, является важной задачей, решаемой при обеспечении технической защиты информации от утечки за счет побочных электромагнитных излучений (ПЭМИ) [1 – 11]. При этом на практике обычно используется инструментально-расчетная методика, основанная на предварительном измерении уровней напряженности полей вблизи ТС в некоторой опорной точке, например, на расстоянии 1 м, и последующем пересчете этих данных в точку на границе КЗ. Причем для заданных условий и допущений [3, 8] расчет коэффициента ослабления уровней напряженности как электрического, так и магнитного полей осуществляется с использованием одной и той же формулы.

Однако, как показывает анализ, в общем случае это должны быть различные формулы и неучет этого обстоятельства может в ряде ситуаций приводить к существенной недооценке уровней напряженности полей ПЭМИ на границе КЗ. Цель работы – на основе использования известных точных решений для излучающих элементарных электрического и магнитного диполей (ЭЭД и ЭМД), моделирующих ТС как излучателей ПЭМИ, предложить методический подход к оценке минимально возможного ослабления уровней напряженности электрического и магнитного полей ПЭМИ при распространении из опорной точки до точки на границе КЗ. Впоследствии с помощью такой методики можно будет легко провести мажорирующую оценку прогнозируемых уровней напряженности полей ПЭМИ на границе КЗ.

Основные положения методического подхода

В общем случае тип излучателя ПЭМИ неизвестен. В связи с этим для аналити- ческих оценок ограничимся рассмотрением простейших моделей излучателей в виде ЭЭД (рис. 1а) и ЭМД (рис. 1б). С электродинамической точки зрения такое приближение вполне законно для анализа ПЭМИ от ТС на сравнительно низких частотах, когда характерный размер диполей много меньше длины волны [9, 10].

Тогда согласно [10. 11] комплексные амплитуды напряженностей электрического и магнитного полей, можно рассчитать по формулам:

♦ для ЭЭД:

£(ГИgWL i । x " r I I

♦ для ЭМД:

v 7                г I ikr I ’ expt-zb*)^ , 1     1 ]

где                – комплексные константы (в дальнейшем не существенные), k = 2π/λ – волновое число, i – мнимая единица.

Анализ формул (1) – (4) показывает, что если в опорной точке на расстоянии d от излучателя уровни напряженности электрического (магнитного) поля E ₀ ( H ₀ ), рассчитанные для случая ЭЭД и случая ЭМД, принять равными, то в другой точке, в частности, в точке на границе КЗ или ином расстоянии R ₂ ( рис. 1 ), эти уровни напряженности электрического (магнитного) поля E ₂ ( H ₂ ) могут существенно отличаться из-за различного характера ослабления полей на трассе распространения.

Коэффициенты ослабления уровней напряженностей электрического ( K _эE (r) и магнитного ( K _эH (r) полей, создаваемых ЭЭД (в формулах индекс « э »), будем рассчитывать по формулам:

Рис. 1. Модели излучателей ПЭМИ: a) ЭЭД; б) ЭМД

4<-')H4)|/W)|.|к„иН4'№И

Тогда с учетом (1), (2) и (5) получим:

K_E, дБ q

-10

-20

-30

-40

-50

a

-60

-70

-80

-90

-100

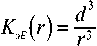
4Y-kV*\ k4d4 -k2d2 + 1

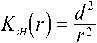
W±1 k²d² +1

0     10     20    30     40    50     60    70     80    90    100

,f МГц

Аналогично с учетом (3), (4) и (5) для коэффициентов ослабления уровней напряженностей электрического K _мE (r) и магнитного K _мH (r) полей, создаваемых ЭМД (в формулах индекс « м ») получим:

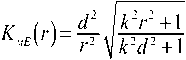
- (kVZkV±Lm[ > rJ^k4d4-k2d2+V

Из сравнения соотношений (10) – (11) с соотношениями (12) – (13) следует:

^,ДБ о

-10

-20

-30

-40

б

-60

-70

-80

-90

-100

К,еН = Кл.нИ

О 10     20    30     40    50     60    70     80    90    100

f МГц

K3H^VKa.eH

Равенство (10) доказывает, что использование коэффициента ослабления по

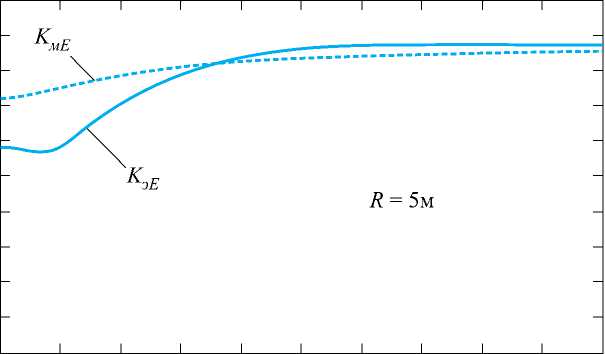
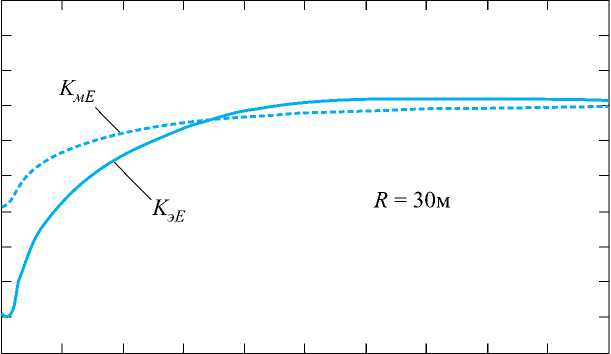
Рис. 2. Частотные зависимости коэффициентов ослабления по электрическому полю для ЭЭД (а) и ЭМД (б)

электрическому полю в модели излучателя в виде ЭЭД эквивалентно использованию коэффициента ослабления по магнитному полю в модели излучателя в виде ЭМД. Аналогичный вывод в отношении коэффициентов ослабления по магнитному полю ЭЭД и электрическому полю ЭМД следует из равенства (11). Однако заранее не известно, к какому типу излучателя (ЭЭД или ЭМД) относится данное ТС, создающее ПЭМИ. При этом возможная ошибка в классификации ТС как излучателя опасна своим следствием – занижением уровней полей ПЭМИ на границе КЗ, что может привести к неверному выводу относительно защищенности информации от ее утечки за счет ПЭМИ. Для иллюстрации указанных особенностей на рис. 2 для фиксированных значений расстояния до границы КЗ 5 и 30 м приведены частотные зависимости коэффициентов ослабления уровня напряженности электрического поля, рассчитанные по (6) и (8), соответственно для ЭЭД и ЭМД.

Из анализа графиков, приведенных на рис. 2 , следует, что расхождение между значениями коэффициентов ослабления по электрическому поля для этих двух модельных излучателей на низких частотах порядка единиц МГц и ниже может достигать 30 дБ при 30 м и 15 дБ при 5 м. На более высоких частотах порядка нескольких десятков МГц и выше расхождение не столь значительное, не более 2 – 4 дБ. Отметим, что эта погрешность вполне соизмерима с инструментальной погрешностью измерений, проводимых при оценке защищенности информации, обрабатываемой ТС, от утечки за счет ПЭМИ [5].

Как показывает анализ, выбор формулы для расчета коэффициента ослабления по тому или иному виду поля может существенно сказаться на оценке максимальной дальности R ₂ перехвата ПЭМИ (зоны R ₂ ). В связи с этим приведем некоторые примеры расчетов.

Рассмотрим ТС в виде модели элементарного диполя, тип которого (ЭЭД или ЭМД) заранее неизвестен. Допустим, что в опорной точке на расстоянии 1 м от диполя измерен уровень напряженности электрического поля, который составил, например, Е ₀ ( рис. 1 ).

Сначала предположим, что диполь электрический. Тогда уровень напря-

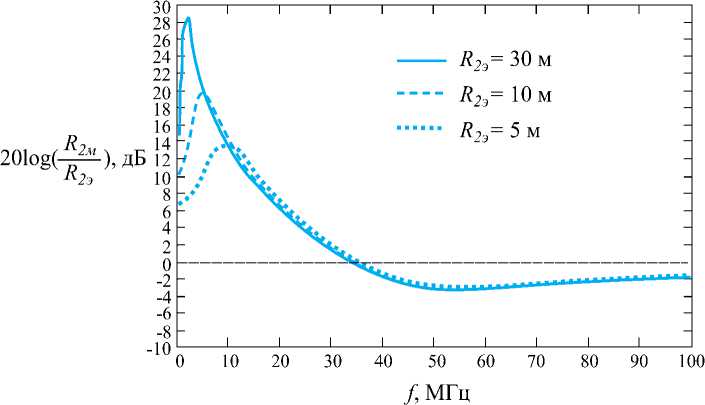
Рис. 3. Частотная зависимость отношения радиусов R2м /R2э , рассчитанных при моделировнии ТС различными типами диполей

женности электрического поля в точке на удалении r ( r ≥ d ) от диполя будет:

E(r) = E 0 K эE (r) .                     (12)

Предположим, что радиус R ₂ зоны возможного перехвата ПЭМИ определяется в основном значением электрического поля E ₂ ПЭМИ на какой-то одной частоте f (например, это может быть ядром спектра ПЭМИ). Тогда для определения радиуса R ₂ , (индекс « э » – указывает на предполагаемый тип диполя, моделирующего ТС) можно на основании (12) записать соотношение:

E2 = E0KэЕ (R2э).(13)

Теперь предположим, что диполь – магнитный. Тогда по аналогии с (13) можно записать:

E2 = E0KмЕ (R2м).(14)

Приравнивая (13) и (14), получаем соотношение

KмЕ (R2м) = KэЕ (R2э),(15)

из которого с учетом (6) и (8) следует уравнение для определения отношения радиусов R _2м /R _2э , рассчитанных в различных предположениях о типе диполя.

Некоторые результаты расчетов отношения R2м /R2э в зависимости от частоты f приведены на рис. 3. Выбирая из двух величин R2м и R2э наибольшую, можно провести мажорирующую оценку радиуса R2.

Как следует из графиков, приведенных на рис. 3 , на частотах примерно менее 36 МГц в качестве R ₂ следует выбрать величину R _2м , поскольку она больше, и соответственно для расчета коэффициента ослабления – формулу (8).

Если выбрать, наоборот, в качестве R ₂ величину R _2э и проводить расчет коэффициента ослабления соответственно по формуле (6), то в оценке величины R ₂ можно в некоторых случаях ошибиться в десятки раз.

На частотах свыше примерно 36 МГц целесообразно в качестве R ₂ выбрать величину R _2э , поскольку теперь она больше, и соответственно для расчета коэффициента ослабления по электрическому полю – формулу (6). Вместе с тем в этом частотном диапазоне эффект от перепутывания формул для проведения мажорирующей оценки радиуса R ₂ не столь велик – отличие R _2м от R _2э составляет не более 1,5 раза. Таким образом, коэффициент ослабления K _E (r) по электрическому полю предлагается рассчитывать как

K E (r) = max{K эE (r), K мE (r)}.        (16)

Аналогично коэффициент ослабления K _Н (r) по магнитному полю предлагается рассчитывать как

K Н (r) = max{K эН (r), K мН (r)}.      (17)

Для удобства выявления областей параметров, при которых, например, величина превалирует над величиной K _мE (r) и наоборот, введем вспомогательную функцию, описывающую отношение коэффициентов ослабления по электрическому полю, рассчитанных для различных типов диполей:

kYj^dll_^е^ = N_kYjjn^=£^ (18)^(r) pd^kV+i F^

у kV*k2d2

где обозначено

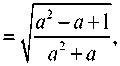
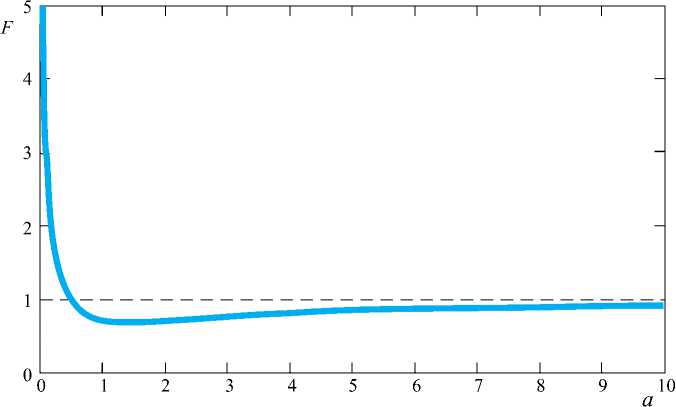
Рис. 4. Зависимость F(a)

F^ =

Zr-6 + l

ЬЧЪ

a = (kr) ² = (2 π rf/c) ² ,

b = (kd) ² = (2 π df/c) ² .

Зависимость F(a) представлена на рис. 4 .

Она имеет следующие особенности: при a > > 1 F(a) ≈ 1, при a = 1 F(a) = 1 / √ 2 , при a <<  1 F(a) = 1/ √ a . Используя эти особенности, можно проанализировать другие частные, но важные случаи поведения функции γ(a,b) .

Так, предположим, что точка на границе КЗ находится на расстоянии r = 50 м и попадает в дальнюю зону излучения, т.е. реализуется случай a >> 1 . Частоты, при которых выполняется приближенное условие дальней зоны (kr) ² ≥ 4 , будут f ≥ 2 МГц. На этих частотах F(a) ≈ 1 и поэтому формула (18) примет вид:

1     / Ь² +Ь ПЛГ^+к²^²

г = —т =  --- = а^-.— —(19)

F^ W-b+I U-V-k2d2 + l

На рис. 5 приведена зависимость γ (b) , рассчитанная по формуле (19).

При γ <  1 коэффициент ослабления, рассчитанный по формуле (8), больше, чем коэффициент ослабления, рассчитанный по формуле (6); при γ >  1 – наоборот.

Переходную точку b, в которой значения коэффициентов ослабления одинаковы, найдем из условия:

y^^ + b^^-b + l^l, откуда b = (2πdf/c)2 = 0,5. Отсюда, считая, что d = 1 м, получаем гранич-

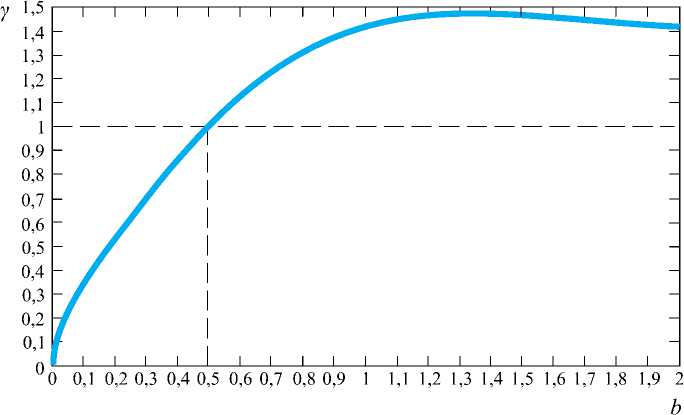
Рис. 5. Зависимость γ (b)

ное значение частоты f _гр ≈ 36 МГц, выше которой для расчета коэффициента ослабления по электрическому полю следует применять формулу (6) и ниже которой – формулу (8).

Если расстояние r невелико, то значение f _гр следует искать из уравнения

kV-k2r2 + l k4d4-k2d2 + l k4r4 + k2r2 ~ k4d4 + k2d2 ’ которое непосредственно вытекает из (18) при равенстве γ = 1.

На рис. 6 приведены зависимости γ(a,b) , рассчитанные по формуле (18) при различных отношениях a/b .

Анализ графиков, приведенных на рис. 6, показывает, что, несмотря на широкие вариации отношения a/b от 2 до 1000, область переходных точек b достаточно узкая – b ∈ {0,5…1}. Если принять d = 1 м, то в пересчете на граничные частоты эти вариации составят fгр ≈ 34 – 48 МГц.

Для практически важных случаев на рис. 7 приведена рассчитанная по формуле (18) частотная зависимость γ [ a ( f ) , b ( f ) ] при значениях d = 1 м и r = R = 3 , 5 и 50 м.

Из анализа приведенных на рис. 7 графиков следует, что область граничных частот для этих случаев еще уже и составляет f _гр ≈ 34 –38 МГц. При этом, если за среднюю граничную частоту принять значение 36 МГц, то относи-

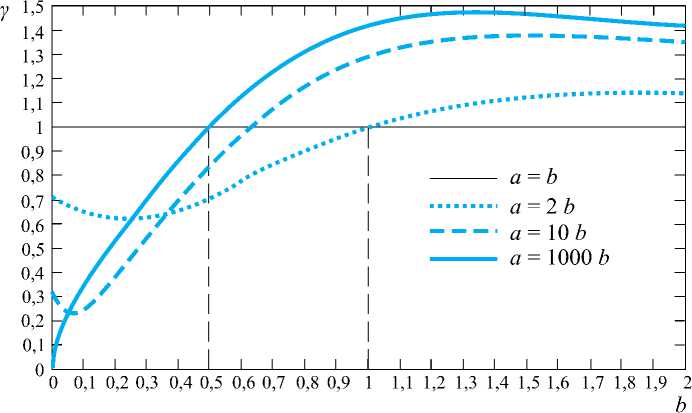
Рис. 6. Зависимости γ (a,b) при различных отношениях a/b

бодном пространстве, однако допускают простое обобщение на случай, когда под диполями имеется идеально проводящая плоскость. В этой ситуации поля реального диполя и его зеркального (относительно плоскости) изображения складываются, причем максимально амплитуды полей могут увеличиться не более чем в 2 раза [9]. В этом случае для приближенных оценок можно принять, что коэффициенты ослабления по электрическому и магнитному полям, определяемые по формулам (20) – (21) (соответственно в неупрощенном варианте – по формулам (16) – (17)), также увеличиваются в 2 раза.

Заключение

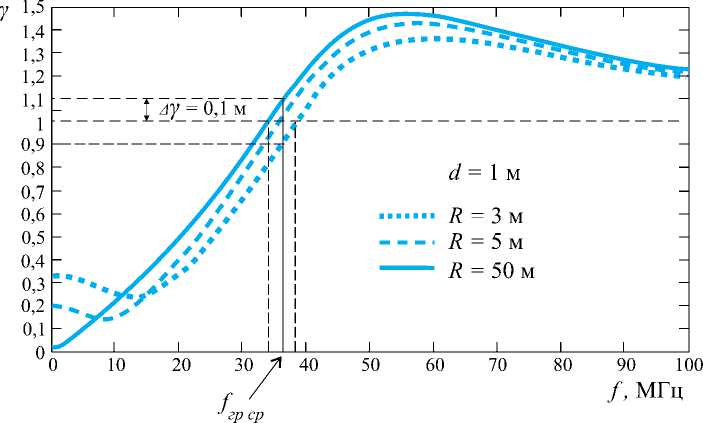
Рис. 7. Частотная зависимость γ [a(f), b(f)]

тельное отклонение γ от единицы не превысит 10%.

Следует отметить, что опорное расстояние d может отличаться от значения, равного 1 м. В этом случае приближенный расчет средней граничной частоты можно провести по формуле fгр ср [МГц] ≈ 36(d0 /d), где d0 = 1 м.

Таким образом, при неизвестном типе излучателя ПЭМИ для мажорирующей оценки уровней напряженностей электрического и магнитного полей ПЭМИ в упрощенном варианте расчета коэффициента ослабления ПЭМИ можно вместо формул (16) и (17) использовать следующие:

К,Г Wt11/ Чгрер K)EV\npu f > fTcp '

^

^к,п (г), при / < £_pcp ^KA.H^aipu f>f_Tcp

Приведенные формулы получены для условий расположения диполей в сво-

Таким образом, показано, что для расчета коэффициента ослабления ПЭМИ следует, в отличие от принятой практики, использовать две различные формулы – отдельно для ослабления уровня напряженности электрического E поля и отдельно для ослабления уровня напряженности магнитного H поля. Показано, что использование только одной формулы может давать заниженные оценки радиуса зоны R ₂ , в частности, на частотах менее 30 МГц – до 30 раз.

На основе использования известных точных решений для излучающих ЭЭД и ЭМД, моделирующих ТС как излучателя ПЭМИ, предложен методический подход к оценке минимально возможного ослабления уровней напряженности электрического и магнитного полей ПЭМИ при распространении ПЭМИ из опорной точки до точки на границе КЗ. Данный методический подход позволяет сравнительно просто провести мажорирующую оценку прогнозируемых уровней напряженности полей ПЭМИ на границе КЗ.

Приведенные формулы обобщены на случай, когда под ЭЭД и ЭМД имеется идеально проводящая плоскость ■