Mechanism and Algorithm for Indirect Schema Mapping Composition

Published Online October 2009 in MECS

Many data management tasks, such as data translation, information integration, and database design require manipulation of database schemas and mappings between them[1]. Schema mappings define the relationship between instances of two given schemas which can be divided into direct and indirect ones by the relationships of elements. Indirect mappings are widely existed, especially when schemas evolve, most mappings that used to be direct become indirect. In indirect mappings, elements between schemas are not directly associated, but related by some algebra operations.

Mapping composition refers to combining two mappings into a single one, which is useful for a variety of data management problems. Figure 1 shows a topology of a data sharing network, each node can be a data sources, an integrated data center or a logical mediator. When data are exchanged from node E to the integrated schema G, instances of E should be translated to G by mapping sequences: E — C, C — A and A — G, and chaining mappings at run-time may be expensive because we may need to follow long and possibly redundant paths in the network. Note that different paths between a pair of nodes may yield different sets of query answers. To ensure the reliability of data exchange, we usually need to get all of the possible paths, and execute each possible data transplantation process according to the paths. Cost of performing such work will be quite large when there are a large amount of data sources. If certain nodes leave the network, then we may lose the mapping paths. Addressing these issues raises several static analysis questions regarding the network of mappings, and mapping composition lies at the core of them all. By precomposing a select set of mapping chains in the network, we can directly execute the data exchange between the source schema and the target schema, which leads to significant run-time savings. Moreover, mapping composition arises in many practical settings like data integration, schema evolution and database designing:

In data integration, a query needs to be composed with a view definition. If the view definition is expressed using global-as-view (GAV), then this is an example of composing two functional mappings: a view definition that maps a database to a view, and a query that maps a view to a query result.

In schema evolution, a schema evolves to a new one, and the relationships between the two schemas may be described by a mapping. The original mappings on the old schema can be updated by mapping composition.

In a database design process, schema may evolve frequently via a sequence of incremental modifications. This produces a sequence of mappings between successive versions of the schema until the desired schema is reached, so a mapping from the original schema to the final one is needed, which can be obtained by composing the mappings between the successive versions of the schema. With this mapping, the designer can migrate data from the old schema to the new schema.

Manuscript received Febuary 11, 2009; revised June 21, 2009; accepted July 21, 2009.

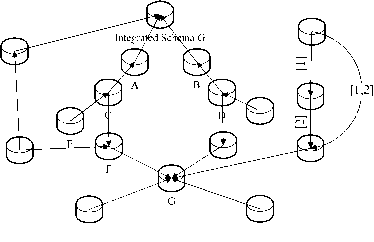
Figure 1. The topology of a data sharing network.

Another motivation for mapping composition comes from the framework of model management[2]. One of the basic operators in model-management algebra is composition, and mappings are treated mostly as syntactic objects. Mapping management can be achieved by defining the composition and inverse operations.

Query composition is widely supported by most of the commercial data management tools, while the mapping composition is still rest on researches and experiments. If the mappings are functional, we can do the composition similarly as the query composition. However, there are a large number of non-functional mappings, most of which are indirect mappings, and we can not directly give the composition. Different from the query composition, indirect mappings can not be composed directly.

In this paper, we mainly discus the composition problems of indirect mappings, and the rest of the paper is organized as follows. In section 2, we show the related works on mapping composition. In section 3 we introduce some concepts of mapping composition. In section 4 and 5, we firstly define the indirect mappings composition, and then propose an indirect mapping composition algorithm. Section 4 presents the experimental results. And the last part is the conclusion.

II.Related works

Mapping composition is a challenging problem[3] whose difficulty is quite sensitive to the expressiveness of the allowed mappings, and there are several researches on such problem [4, 5, 6, 7, 8], including methods based on tuple generation constraints and schema transformation[9, 10, 6], etc. Those mapping composition methods based on schema transformation define complicated schema transformation operations, which only support the computing of direct mappings, and not for those indirect ones with complex algebra operations between schema elements. Model management is a generic approach to solving problems of data programmability where precisely engineered mappings are required[2]. A model management system supports the creation, compilation, reuse, evolution, and execution of mappings between schemas represented in a wide range of meta-models, where the composition operation is one of the ways to realize mapping reusing.

Researches on indirect mappings mostly consider the definitions and basic operations of non-direct element-to- element mappings between the source and target schemas[11] without any further discussions about composition. Madhavan and Haleby[5] showed that the composition of two given mappings expressed as GLAV formulas may not be expressible in a finite set of first-order constraints. Fagin et al[4]. proved that the composition of certain kinds of first-order mappings may not be expressible in any first-order mappings, even by an infinite set of constraints, because the mapping language is not closed under composition. Nash et al[8]. showed that for certain classes of first-order languages, it is undecidable to determine whether there is a finite set of constraints in the same language that represents the composition of two given mappings. In [4], Fagin et al. demonstrated the second-order mapping language, namely second order source- to-target tuple-generation dependencies (denoted by SOtgd), is closed under composition, and they also present a composition algorithm for this language. The second-order languages uses existentially quantified function symbols, which essentially can be thought of as Skolem function. A tuplegenerating dependency specifies an inclusion of two conjunctive queries, Q1⊆ Q2. It is called source-to-target when Q1 refers only to symbols from the source schema and Q2 refers only to symbols from the target schema. However, for implementation, such kind of languages is not supported by standard SQL-based database tools.

Yu and Popa extended the algorithm of Fagin’s to handle nesting and apply it to some schema evolution scenarios, and they also discussed the optimizations of the composition result. Nash et al^[8]. studied the composition of first-order constraints that are not necessarily source-to-target. They considered dependencies that can express key constraints and inclusions of conjunctive queries Q ₁ ⊆ Q ₂ , where Q ₁ and Q ₂ may reference symbols from both the source and target schema, but the composition of constraints in this language is not closed and whether a composition result exists is undecidable. They also gave an algorithm that produces a composition.

Berstein et al[3]. explored the mapping composition problem for constraints that are not restricted to being source-to-target, which extended the work of Nash and Fagin. They applied a “left-compose” step which allows the algorithm to handle mappings on which the algorithm in [8] fails. They used algebra-based instead of logicbased language to express mappings, which can be directly supported by database tools. We call their method “best effort composition approach” (denoted by BECA). BECA tries to eliminate as many relation symbols from the middle schema as possible. Given schemas σ1、σ2 andσ3 , mappings computed by BECA have the form ofσ1 →σ2′ →σ3, where σ2′ ⊂ σ2. That means, in come cases it may be better to eliminate some symbols fromσ2 successfully, rather than insist on either eliminating all them or failing. Since there may be some elements in the middle schema remain at the end of BECA, the result is not a perfect composition.

A main reason that σ ₂ ′ is not empty after BECA, is that there may be indirect mappings. In this paper, we use a strategy namely schema elements back to solve the problem. Although this method expands σ ₁ : σ ₁ → σ ₁ ′ , it can completely eliminate σ ₂ , and a composed mapping only depends on the source and target schema will be generated.

• III.    Mapping composition

Definition 1 Let R ₁ and R ₂ be two binary relations, the composition R ₁ o R ₂of R ₁ and R ₂ is the binary relation: R ₁ o R ₂ = {( x , y ) : ( ∃ z )(( x , z ) ∈ R ₁ ∧ ( z , y ) ∈ R ₂)} .

Let M = ( S , T , Σ )be a schema mapping model, where S and T are the schemas with no relation symbols in common and Σ is a set of formulas of some logical formulas over < S , T >. Then let Inst ( M )be a binary relation between instances over S and T . We define composition of two schema mappings M ₁₂ and M ₂₃ using the composition of the binary relations Inst ( M ₁₂) and Inst ( M ₂₃).

Definition 2 ^[4] Let M ₁₂ = 〈 S ₁, S ₂, Σ ₁₂ 〉 and M ₂₃ = 〈 S ₂, S ₃, Σ ₂₃ 〉 be two schema mappings such that the schemas S ₁, S ₂, S ₃have no relation symbol in common pairwise. A schema mapping M = 〈 S ₁, S ₃, Σ ₁₃ 〉 is a composition of M ₁₂ and M ₂₃ if Inst ( M ) = Inst ( M ₁₂) o Inst ( M ₂₃) which means that Inst ( M ) = { 〈 I ₁, I ₃ 〉 |( ∃ I ₂)( 〈 I ₁, I ₂ 〉∈ Inst ( M ₁₂) ∧〈 I ₂, I ₃ 〉∈ Inst ( M ₂₃))} ,where I_i is the instance of S_i with 1 ≤ i ≤ 3.

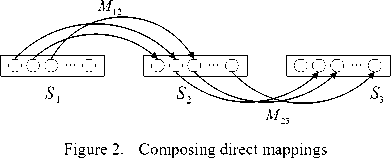
Figure 2 shows an example of direct mapping composition, where S ₂ is the middle schema. Data exchange between S ₁ and S ₃ is achieved by composing M ₁₂ and M ₂₃ . Fagin et al. have proved the existence inevitability of mapping composition, and Alan Nash^[7] gives the prerequisite for the existence of mapping composition, that is two mappings have a common schema, which is consistent with Fagin’s result. Both of them proved the existence of mapping composition by the relationship between query and mappings, and the instance isomorphism.

Example 1: Consider the following schemas S1, S2 and S3 . S1 consists of a single binary relation symbol Maint, which associates the name of maintenance person with the equipment he maintains. Schema S2 consists of a similar binary relation symbol Maint1, which is a copy of Maint, and of an additional binary relation symbol MP, that associates each person with an id. Schema S3 consists of one binary relation symbol Reg, that associates person ids with the equipments the persons take. Consider the following schema mappings      M12 =(S1,S2,Σ12)      and

M ₂₃ = ( S ₂ , S ₃ , Σ ₂₃ ) , where

Σ ₁₂ = { ∀ n ∀ c ( Maint ( n , c ) → Maint ₁( n , c )), ∀ n ∀ c ( Maint ( n , c ) → ∃ sMP ( n , s ))},

Σ ₂₃ = { ∀ n ∀ s ∀ c ( MP ( n , s ) ∧ Maint ₁( n , c )) → Reg ( s , c ))}.

Give the instances of S ₁, S ₂, S ₃as follows:

I ₁ ： Maint^{I 1} ={(A, Eq1),(A, Eq2)}

I ₂ ： Maint^{I 2} = Maint^{I 1}, MP^{I 2} ={(A, 0001) ， (B, 0002)}

I ₃ ： Reg^{I 3}={(0001, Eq1),(0001, Eq2)}

According to Σ ₁₂ and Σ ₂₃ , we have 〈 I ₁, I ₂ 〉∈ Inst ( M ₁₂) and 〈 I ₂, I ₃ 〉∈ Inst ( M ₂₃). By definition 2, if there is a mapping M ₁₃ that satisfies 〈 I ₁, I ₃ 〉∈ Inst ( M ₁₃), then M ₁₃ is the composition of M ₁₂ and M ₂₃ , so M ₁₃ can be expressed as ∀ n ∀ c ( Maint ( n , c ) → ∃ sReg ( s , c )).

Theory 1 The mapping composing operation Inst ( M ₁₂) o Inst ( M ₂₃) = Inst ( M ₁₃) is closed under the homomorphism of instances.

Proof: Given 〈 I ₁, I ₃ 〉∈ Inst ( M ₁₃), for the instances I ₁ ′ and I ₃ ′ , satisfying I ₁ ′ ≅ I ₁ and I ₃ ′ ≅ I ₃ (“ ≅ ”denotes homomorphism), we just need to show that 〈 I ₁ ′ , I ₃ ′ 〉∈ Inst ( M ₁₃). Since Inst ( M ₁₂)and Inst ( M ₂₃)are closed under homomorphism, and Inst ( M ₁₂) o Inst ( M ₂₃) = Inst ( M ₁₃), there exists an instance I ₂ that 〈 I ₁, I ₂ 〉∈ Inst ( M ₁₂) ∧〈 I ₂, I ₃ 〉∈ Inst ( M ₂₃). So there is an instance I ₂ ′ ≅ I ₂ such that 〈 I ₁ ′ , I ₂ ′ 〉∈ Inst ( M ₁₂), and also 〈 I ₂ ′ , I ₃ ′ 〉∈ Inst ( M ₂₃), then 〈 I ₁ ′ , I ₃ ′ 〉 ∈ Inst ( M ₁₃). This was to be shown.

• IV.    Indirect mapping

A direct mappings can be given by a Source-to-Target tuple generating dependency (denoted by S2Ttgd): ∀ x ( φ _S ( x ) → ∃ y ψ _T ( x , y )), where φ _S and ψ _T are respectively the formulas on S and T , and x, y are the set of variables. A full S2Ttgd mapping can be expressed by ∀ x ( φ _S ( x ) → ψ _T ( x )), and a mapping expressed by ∀ x ( φ _S ( x ) → ∧ _i ^k _{= 1} R_i ( x_i ))equals to the set of some full S2Ttgds ∀ x ( φ _S ( x ) → R_i ( x_i )), where i = 1, K , k , and R_i (x) is the atomic formula.

• A. Describe indirect mappings

In indirect mappings, the algebra operation results of the elements in both the source and target schema are related, as shown in figure 3.

S 1                               S 2

M 12 --ЧП^^[2]

• Figure 3.    Indirect mappings

In element correspondence “[1]” (see Fig. 3), nodes in the pane of the source schema are mapped to an element in the target schema after some algebra operations. The algebra operations of schema elements includes some basic ones, like Union, Cartesian, Projection and Selection, and some compositions, like Intersection, Join, Nature Join and division etc.

Definition 3 Indirect elements correspondence (denoted by ICO E ) is the set of element correspondences that elements are mapped after some algebra operations. Let φ _S be the formulas of S , and S _i be the scheme of S , the algebra operations have six forms, as shown bellow, where 1~4 are the basic ones and 5~6 can be derived from 1~4:

Union Let φS(x)=∧(Si(x)∨K ∨Si(x)),Si(x)∈S, k,i and it is the same forψT .

ICO E :      ∀ e ( S ₁( e ) ∨ S ₂( e ) ∨ L ∨ S_n ( e )→ T ( e ))      (or

∀ e ( S ₁( e ) ∨ S ₂( e ) ∨ L ∨ S _n ( e )→ ∃ wT ( e , w )) if there is an existence quantifier).

Cartesian φ _S ( x ) = _∧ ( S_i ( x ) × K × S_i ( x )), S_m ( x ) ∈ S

ICO E :      ∀ e ( S ₁( e ) × S ₂( e ) × L × S_n ( e ) → T ( e ))     (or

∀ e ( S ₁( e ) × S ₂( e ) → ∃ wT ( e , w ))).

Projection φ _S ( x ) =_∧ ( π _{k 1, K km} ( S_k ( x ))), S_k ( x ) ∈ S .

k

ICO E : ∀ x( π _{m , n} ( S ₁ ( a ₁ , a ₂ , K , a _{n 1})) ∧ π _{l , k} ( S ₂ ( b ₁ , b ₂ , K , b _{n 2}))

Let ⊗ ={∧,∨,σ,θ}be the basic algebra operation symbol set (see 1~4 in definition 3), and indirect mappings can be expressed as φS′ (x) = ⊗(πi1 im (Sk)), Sk (x) ∈ S. Take the indirect k      k,K k mapping shown in figure 4 as an example, M12 can be expressed as:

∀ x(( π m ₁ ( R ₁ ^{S 1}( x 1¹ )) ⊗ π n ₁ ( R ₁ ^{S 1}( x 1² ))) ∧ ( π m ₂ ( R_k^{S 1}( x k ¹ ))

⊗ π n ₂( R_k^{S 1} ( x k ² ))) → ∃ y ( R ₁ ^{S 2} ( y 1 ) ∧ π l R 2 ^{S 2} ( y 2 ))), and M ₂₃ :

∀ y( R ₁ ^{S 2} ( y 1 ) ∧ ( π l ( R ₂ ^{S 2} ( y 1¹ )) ⊗ π p ( R 2 ^{S 2} ( y 1² ))) → ∃ z( R ₁ ^{S 3} ( z 1 ) ∧ R 3 ^{S 3} ( z 2 ))) .

If ψ _T ′ ( x , y ) has the same form with φ _S ′ ( x ), then the nonfull indirect mapping can be expressed as: ∀ x( φ _S ′ (x) → ∃ y ψ _T ′ (x,y)).

^M 12

|                      | о op \

S ₁                 S ₂                           S 3

M 23

• Figure 4.    Indirect mappings between schemas.

B.Exchange data under indirect mappings

Now we give the concept of homomorphic instances under indirect mappings ( concept of homomorphic direct mappings is given in [4], and we do not discuss it here). Consider the following example:

Example 2: Given schemas S ₁, S ₂and S ₃ . S 1 consists of a single binary relation symbol Consistof , which associates the name of equipments with the parts they have. S ₂ consists of a similar binary relation symbol Consistof 1 , which is a copy of Consistof , and of an additional binary relation symbol MCode , that associates each equipment name with an id. S ₃ consists of a single binary relation symbol MRegister , which associates the code of equipments with the related parts. Consider the following mappings: M ₁₂ = ( S ₁, S ₂, Σ ₁₂) and M ₂₃ = ( S ₂, S ₃, Σ ₂₃), where

Σ ₁₂ = { ∀ e ∀ p ( Consistof ( e , p ) → Consistof ₁( e , p )), ∀ e ∀ p

→ T ( a_m , a_n , b_l , b_k , K ))(or ∀ x( π _{m , n} ( S ( a ₁, a ₂, K , a_{n 1})) ∧

( Consistof ( e , p ) → ∃ cMCode ( e , c ))},

π _{l , k} ( S ( b ₁, b ₂, K , b_{n 2})) → ∃ y T ( a_m , a_n , b_l , b_k , K , y ₁, y ₂, K , y_{n 3}))

), where x and y are the set of variables.

• 1.    Selection This operation considers the conditional mappings, which represents the user’s integrality. It has the form of

• 2.    Intersection refers to several schemas, which is a kind of selection operation essentially.

• 3.    Join is the composition of Cartesian and Selection

φ _S ( x ) = _∧ ( σ _F ( S_i ( x ))) = _∧ ( S_i ( x ) ∧ F ( t )), S_i ( x ) ∈ S , t ∈ Inst ( S ) . ii

ICO E : ∀ e (( S ( e ) ∧ ( Inst ( e ) | = θ )) → T ( e )).

Σ ₂₃ = { ∀ e ∀ c ∀ p ( MCode ( e , c ) ∧ Consistof ₁( e , p )) → MRegister ( c , p ))}

The second formula in Σ ₁₂ is a direct mapping that associate equipment name e in the source schema to the equipment name e in the target schema. According to Theory 1 , let I , J be the instance of a mapping M , that means 〈 I , J 〉∈ Inst ( M ), and if there is an instance pair 〈 I ′ , J ′ 〉 that 〈 I ′ , J ′ 〉 ≅ 〈 I , J 〉 , then 〈 I ′ , J ′ 〉∈ Inst ( M ). For the converse, if 〈 I ′ , J ′ 〉 and 〈 I , J 〉 are respectively the instance of M , then we have 〈 I ′ , J ′ 〉≅〈 I , J 〉 . The above conclusion is true for that M is the direct mapping. For the indirect mappings, the homomorphism between instances is different. For example, let S ₁ ′ be a schema,

which is a copy ofS1 with a little differences that certain element in S1 splits into several parts in Si. For example, the equipment name in S‘ contains two parts (supername+name), and the corresponding formula set is X’2. Therefore, under the condition of homomorphism, there may be some non-one-to-one correspondences.

Let S、T be the source and target schema respectively, and Ri is a scheme of S. If there is an indirect mapping M from S to T, and let Ri be the scheme constructed as follows: substituting each element combination that participates in the indirect mappings with a single element. We call Ri a generating scheme. If we define mappings from Rii to T with the form of Vx(R/(x) > ^T (x)) , and mappings from Ri to T with the form of Vx(Ri(x) —Indirect > ^T (x)) , then mappings from Ri to yT (x) are direct, and those from Ri (x) to ^T (x) are indirect, as shown in figure 5:

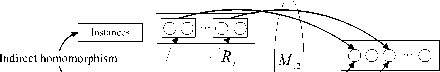
Figure 5. Instance homomorphism under indirect mappings

We define the homomorphism function h under indirect mappings as:

h ( a i ) =

e            , e e Inst( n k ( R i ))

compound ( e 1 , к , e l ), e i e Inst( n i ( R j ))

Then h is called a general homomorphism function , where compound is the algebra operation of elements.

Definition 4 Let R and R' be two schemas, h is the general homomorphism function shown above. Let J, J' be the instances ofR and R' respectively. If for each scheme symbol Ri in R , and each tuple (a1, к, an) e RJ , there is a tuple (h(a1),K, h(an)) e RJ , then R and R are homomorphic instances under h , then the data exchange process under indirect mappings can be implemented by the homomorphism given in Definition 4 comparing with the process under direct mappings (see[12] ).

V. Mechanic of indirect mapping composition

• A.    Schema-elements-back

As shown in figure 4, although there is a common schema S2 , we can not directly construct the mappings from S1 to S3 according to M12 andM23 , even can not give the mapping composition directly. Using direct mapping composition, elements in S1 can only map to part of the certain elements of S3 . During the data exchange procedure, a complete instance of S3 may consist part of the instance from S2 , so data exchange from S1 to S3 by direct mapping composition M12 o M23 may lose some information, that is because M12 andM23 contains some elements that is not in common, there is no such an instance I2 of S2 satisfying conditions in Definition 2.

Since the expressions of indirect mapping composition can not be derived by Definition 2 directly, we deal with this problem based on general instance homomorphism, the main idea of which is to construct a schema that can be directly used for mapping composition, and make sure that the instances of the constructed schema is homomorphic with the instances of the original schema under the general instance homomorphism function . We propose a strategy named schema-elements-back by constructing some virtual elements in the source schema to deal with the composition of indirect mappings. Compared with BECA, schema-elements-back can eliminate the infection of the middle schema.

Definition 5 Let M _ST = ( S , T , X _ST ) be a model of indirect schema mapping, where X ST is the formula set with the form of V x( ^ S (x) >  3 yy'_T (x,y)), and mappings from S to T are sound^[13]. Let Dom_M ( S ) be the domain of S , and Dom ( T ) be the domain of T , and then we have Dom M ( S ) c Dom(T ) . Let y _In and x _In be the set of variables that participate in the indirect mappings in T and S respectively, and we construct the virtual elements in S by set y _In - x _In . As shown in figure 6, the newly constructed source schema is denoted by S' . We can construct direct mappings from T to S' on DomM ( DomM ( S )) . Let M S _T be the mapping from S' to T , and M ST be the inverse of M S , _T , and then the process of virtual elements construction is called a schema-elements- back process.

M ST

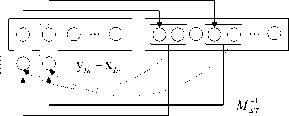
Figure 6. Inverse of indirect mappings based on virtual elements

Definition 6 Let M ₁₂ = ( S 1 , S 2 , X ₁₂ ) and M 23 = ( S ₂, S 3 , X ₂₃ ) be two indirect schema mappings such that the schemas S ₁, S ₂, S ₃have no relation symbol in common pairwise. We construct a new schema S ^ by adding virtual elements according to Definition 5 with the mapping M 1 - 2 and its inverse M 1' ₂ . Let M = ( S 1 , S 3 , £ 113 ) be the newly constructed mapping model. If Inst ( M ) = Inst ( M 12 ) o Inst ( M ₂₃) , that means Inst ( M ) = « I ', 1 3 ) I ( 1 ₂X < I ', 1 2 ) e Inst ( M 12 ) л( 1 2 , 1 3 ) e Inst ( M 23 ))} , then M is the composition of indirect mappings M ₁₂ and M ₂₃ .

• B.    Indirect mapping composition algorithm

When data are exchanged under the strategy of schema-elements-back , instance of some elements in the middle schema may be firstly transformed to the source, and there is a reverse data flow during the data exchanging process from the source to the target. Such a data flow can be implemented by the reverse mapping from the element in the middle schema to the newly added element in the source schema. Since the object of composing two schema mappings is to directly construct the mapping from the source to the target without considering the middle schema, schema-elements-back can insure that under the condition of indirect mapping, directly data exchange from the source to the target can be realized, which can improve the efficiency of data transformation. Now we show the process of indirect mapping composition.

Schema-elements-back is the process of adding new elements to the source schema according to the middle schema, in order to achieve a directly mapping from the source schema to the target schema under the condition that new elements are introduced. As shown in figure 7, the dashed lines represent the correspondences between the newly added schema elements and elements in the middle schema, from which we can see that when S1 is translated to S1′ , by Theory 2, mapping composition M1′3 can be directly constructed from S1′ to S3 .

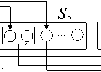
Figure 7. Process of Schema-elements-back

M 12

S ₁ ′ S

Lkincnl

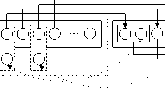
S 3

M 23

Now we give an indirect mapping composition algorithm (denoted by IMCA), without loss of generality, we consider the case shown in figure 7, and for the other cases we just need some small modifications.

Algorithm IMCA

Input: M ₁₂ = ( S ₁, S ₂, Σ ₁₂) and M ₂₃ = ( S ₂, S ₃, Σ ₂₃), where Σ ₁₂ and Σ ₂₃ are extended S2Ttgds that describe indirect schema element correspondences.

Output: A schema mapping M _{1 ′ 3} = ( S ₁ ′ , S ₃, Σ _{1 ′ 3}), which is the composition of M ₁₂ and M ₂₃ .

Step1. Normalize Σ ₁₂ and Σ ₂₃ :

Rename the function and element symbols so that the symbols that appear in Σ ₁₂ are all distinct from those in Σ ₂₃ .

Step2. Construct virtual elements in S ₁ :

If       M 12 :       π_{θ 1}( R_{i 1} ^{S 1}( x_{i 1})) → π_{θ 2}( R_i^S ₂²( x_{i 2}))      and

M 23 : π_{θ 2 ′} ( R_i^S ₂²( x_{i 2})) → π_{θ 3}( R_i^S ₃³( x_{i 3}))satisfying that θ ₂ ′ ⊃ θ ₂.

Then For each i do projection operation π_{θ ′ - θ} R_i^{S 2} ( x_i ), and get an attribute set E = { E ₁ , K E_l }, where E _i is the set of attributes generated by π_{θ ′ - θ} R_i^{S 2} ( x_i ).

Add each set E_i into S ₁ and combine it with attributes computed by π_θ ( R_i^{S 1} ( x_i )), which is called a schema elements back process. As shown in the left dashed box of figure 7, we get the new constructed schema S ₁ ′ by combining elements in E to S ₁ ( virtual elements are from S ₂ ). Then we get the mapping M _{1 ′ 2} from S ₁ ′ to S ₂ with the formula set Σ _{1 ′ 2} . Since the mapping from S ₂ to S ₁ ′ is one-to-one, we get M ₁ ^- _{′ 2} ¹ = M _{21 ′} , where Σ _{21 ′} gives the data back rules from S ₂ to S ₁ ′ during the data exchange process from S ₁ ′ to S ₃ .

Step3. Construction of S ₁₂ and S ₂₃

• ( 3.1 )    Initialize S ₁₂ and S ₂₃ to each be the empty set.

Assume the formulas in Σ _{1 ′ 2} is

( ∀ x ₁( φ ₁ → ψ ₁)) ∧ K ∧ ( ∀ x_n ( φ _n → ψ _n ))

• ( 3.2 )Pu t each of the n implications φ _i → ψ _i , for 1 ≤ i ≤ n , into S ₁₂ . We do likewise for Σ ₂₃ and S ₂₃ . Each implication χ in S ₁₂ has the form φ (x) → ⊗ ( π_θ ( R^S_j ²(x _j )) ⊗ K ⊗ π_θ ( R_j^{S 2}(x _j ))) where every

member of x is a universally quantified variable, and each x _j , for1 ≤ j ≤ k , is a sequences of terms on x .

• ( 3.3 )Re place each such implication χ in S 12 with k implications:

φ (x) → π θ ( R 1 ^{S 2} (x 1 )) ⊗ K ⊗ π θ ( R 1 ^{S 2} (x 1 )), K , φ (x) → π θ ( R k ^{S 2}(x k )) ⊗ K ⊗ π θ ( R k ^{S 2}(x k )).

Step4. Compose S 12 and S 23 :

Repeat the following until every schema symbol in the left-hand side of every formula in S 23 is from S 1 .

For each implication χ in S 23 of the form ψ → γ where there is an atom R ( y ) ( R is a scheme symbol in S 2 ), perform the following steps to replace R ( y ) with atoms in S ₁ ′ .

• ( 4.1 )    Let φ ₁ → R ( t ₁), K , φ _p → R ( t_p )be all the formulas in s 12 whose right-hand side has R in it. If no such implications exist in S ₁₂, we remove χ from S ₂₃. Otherwise, for each such formula φ _i → R ( t_i ), rename the variables in this formula so that they do not overlap with the variables in χ .

• ( 4.2 )    Remove χ from S ₂₃ and add p formulas to S ₂₃ as follows: replace R ( y ) in χ with φ _i and add the resulting formula to S 23 , for 1 ≤ i ≤ p .

Step5. Construct M 13 :

Let S 23 = ( X i , . , X r ) where X i , k , X r are all the formulas from step4, Let S 1 , ₃ be V z 1 x 1 a . . aV z_rx_r where z , is the set of variables found in x , for 1 ^ i ^ r ■ i i

Return M ₁₃ = ( S ‘ S ₃, S _r3) »

A new source schema should be maintained by the composition algorithm, and such a schema may not be useful in other mapping compositions. However, if the scale of data to be exchanged is large, such new extended schema can improve the efficiency of data exchange.

VI. Experiments

• A.    Complexity of ICMA

Let the elements that schema S 1 , S 2 and S 3 respectively contains be N 1 , N 2 and N 3 . In step1 of ICMA, the rename operation need to match each elements among S 1 , S 2 and S 3 , whose complexity is O ( N 1 x N ₂ x N ₃ ) .

Let the correspondences in M ₁₂ be N ₁₂ and correspondences in M 23 be N 23 , where N 12 and N 23 are the numbers of atom elements. The number of virtual elements constructed in schema-element-back process is N ₂₃ - N ₁₂ , so the complexity for constructing virtual elements is O ( N 23 - N ₁₂ ) .

The complexity for composing is decided by the atom implications that S _r2 and S ₂₃ contains. Let N C be the number of implications in S ₁₂ with the form of ф _i ^ y i and n¹ be the atom formula in y i , and then the number of formulas in S _r2 is N C x n C . If the number of implications with the form of y i ^ y . in S ₂₃ is NC³ , where y i is the set of atom formulas. The number of pairs of atom formulas that should be matched during the replacing process is N C x n i ¹² x N C , so the composing complexity is O ( NC x n C x NC ³) . The whole complexity for indirect mapping composition is O ( N 1 x N ₂ x N ₃) + O ( N ₂₃ - N ₁₂ ) + O ( N C ² x n i ¹² x N C ³) . The complexity of direct mapping composition process is O ( N 1 x N ₂ x N ₃ ) + O ( N C ² x n i ¹² x N C ³) , both are polynomial complexities.

• B.    Results and analysis

• (1)    Query efficiency under indirect mapping composition

Given the numbers of elements in schema S ₁ , S ₂ and S ₃ , and the numbers of implications in S _r2 and S ₂₃ . Given different scales of indirect mappings, now we compute the numbers of virtual elements constructed during the process of schema-element-back . We use the example in DBLP, chose 20 literature base by the sequence of letters, and pick up the meta-information of each literature. We construct the mappings manually as follows (take three of them for example):

Author ® Author ® ■ • ■ ® Author ^ AuthorSet

Country ® University ® l ® City ^ AuthorAddress

Country ® Street ® l ® City ^ ConferenceLocation

The relationship between the number of indirect element correspondences and the number virtual elements constructed are shown in table 1.

Table 1. Relationship between the number of virtual elements generated during the indirect mapping composition process and the number of indirect element correspondences.

( S 1 ^ S 2 )	5	10	15	20	25	30	35	40	45
( S 2 ^ S 3 )	5	11	15	22	23	30	36	45	45
virtual elements	2	5	4	7	5	10	11	9	15

Since virtual elements are introduced during the process of indirect mapping composition, figure 8 show a comparison for numbers related by the queries for nonmapping-composition and mapping-composition respectively.

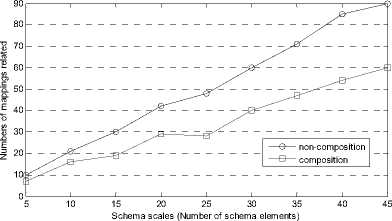
Figure 8. Comparison for mappings related under different condition.

As we can see that, although some virtual elements participate the querying and data exchanging, compared with the non-composition way, indirect mapping composition can reduce the number of mappings related by the query and improve the query efficiency.

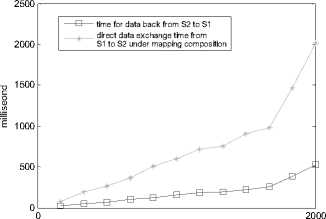
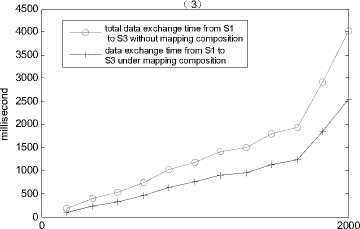
Consider the indirect mappings shown in figure 4, we simulate the data exchange process from S 1 to S 3 , and compare the executing times between indirect mapping composition and non-composition under different scale of instances. We use Oracle 9i as the database, and the time for reading records in the oracle database is the increase function of record scale and attributes numbers.

In the case of non-composition, instances { I 1 } of S 1 are firstly transformed to instances of S 2 according to M 12 , denoted as { I 2 }, then { I 2 } are transformed to { I 3 } of S 3 . the read and write of data happens among three schemas.

In the case of composition, since there are indirect mappings from S 1 to S 3 , using the schema element back given in IMCA, instance for part attributes S ₂ of are firstly transformed to S ₂, and we get the new instances { 1 1 }, then instances { 1 ₃} of S 3 are generated according to M 13 .

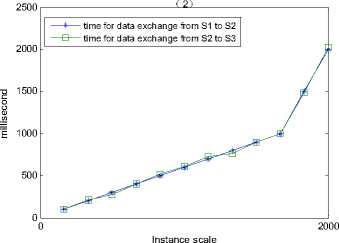
Now we give the executing time (milliseconds) for the data exchange process from S 1 to S 3 under different instance scale of S 1 . Figure 9 show the data exchange executing time comparison results:

（ 1 ）

instance scale

Instance scale

0 0

exchange time from S1 to S2 exchange time from S2 to S3 exchange time from S1 to S2 under non-composition exchange time from S2 to S1 exchange time from S1 to S3 total exchange time from S1 to S3 under mapping composition

instance scale

Figure 9. data exchange process executing time comparisons.

• (2)    Comparison of BECA and IMCA

In BECA, symbols in the middle schema are eliminated by some algebra operations step by step using view unfolding, left composing and right composing. The main idea of BECA is to replace the symbols in the middle schema by the symbols in the source and target schemas as much as possible. Let the elements that participate in the process of elimination obey the equality distribution, and the numbers of virtual elements are decided by step 2 of IMCA, figure 10 shows the comparison between number of element symbols eliminated by BECA and number of virtual elements constructed in IMCA.

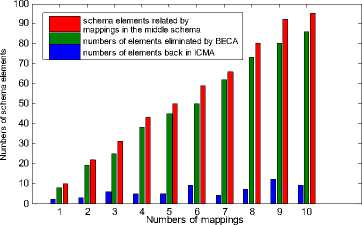
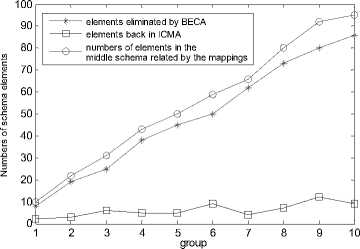
Figure 10. Comparison for affection of middle schema between BECA and ICMA

Seen from the results, the affections of the middle schema on both BECA and IMCA are almost the same. Besides, number of virtual elements in IMCA and number of elements in the middle schema that is not eliminated are equal. But using IMCA, we can completely eliminate the affection of middle schema, which can be seen as a real composition process.

VII. Conclusion

Mapping composition is an active aspect in the research of schema mapping management, the object of which is to reuse mappings as a model, and simplify the process of data exchange. Especially when the scale of peers in the network is large, composing mappings can improve the data exchange efficiency. In this paper, we give the definition of indirect mappings, and discuss the composability of indirect mappings. Then we propose an indirect mapping composition algorithm using the schema-element-back strategy. Experiment results show that although IMCA dose not improve the query performance, but the affection of middle schema can be eliminated.