Medical Image Denoising Using Bilateral Filter
Автор: Devanand Bhonsle, Vivek Chandra, G.R. Sinha
Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp
Статья в выпуске: 6 vol.4, 2012 года.
Бесплатный доступ
Medical image processing is used for the diagnosis of diseases by the physicians or radiologists. Noise is introduced to the medical images due to various factors in medical imaging. Noise corrupts the medical images and the quality of the images degrades. This degradation includes suppression of edges, structural details, blurring boundaries etc. To diagnose diseases edge and details preservation are very important. Medical image denoising can help the physicians to diagnose the diseases. Medical images include MRI, CT scan, x-ray images, ultrasound images etc. In this paper we implemented bilateral filtering for medical image denoising. Its formulation & implementation are easy but the performance of bilateral filter depends upon its parameter. Therefore for obtaining the optimum result parameter must be estimated. We have applied bilateral filtering on medical images which are corrupted by additive white Gaussian noise with different values of variances. It is a nonlinear and local technique that preserves the features while smoothing the images. It removes the additive white Gaussian noise effectively but its performance is poor in removing salt and pepper noise.
Image denoising, Bilateral filter, AWGN, Medical images
Короткий адрес: https://sciup.org/15012332
IDR: 15012332
Текст научной статьи Medical Image Denoising Using Bilateral Filter
Published Online July 2012 in MECS
Medical imaging includes magnetic resonance imaging, x-ray imaging, computer tomography, ultrasound imaging etc .All these images are collected by different types of sensors and they are contaminated by different types of noises [1,2] such as additive white Gaussian noise (AWGN)[3], speckle noise [4-9] , salt and pepper noise[10], rician noise[11], Brownian noise etc. Generally MRI images are corrupted by rician noise while ultrasound images are corrupted by speckle noise. In the digital image, noises are high as well as low frequency components. It is very easy to remove high frequency components whereas it is difficult to remove low frequency components because real signal and low frequency noise cannot be distinguished easily. Noise may be generated due to imperfect instruments used in image processing, problems with the data acquisition process and interference; all of which can degrade the data. Furthermore, noise can also be introduced by transmission errors and compression also. Different types of noises [11] are introduced by different noise sources like dark current noise is due to the thermally generated electrons at sensor sites. It is proportional to the exposure time and highly dependent on the sensor temperature. Shot noise [12], which has the characteristics of Poisson distribution [11], is due to the quantum uncertainty in photoelectron generation. Amplifier noise and quantization noise occur during the conversion of number of electrons to pixel intensities. Ultrasound imaging is the example of coherent imaging and they are severely affected by speckle noise [7,8]. Speckle is a type of multiplicative noise. This is generated due to scattering phenomenon. A number of elementary scatterers reflect the incident waves towards the sensors. The back scattered coherent waves with different phases undergo constructive and destructive interference in random manner [5]. Therefore acquired image is corrupted by a random granular pattern which is called as speckle. In medical term it is commonly referred as “texture” [5].
The overall noise characteristics in an image depend on many factors, which include sensor type, pixel dimensions, temperature, exposure time [13] etc.
It is necessary to denoise the medical images before analyzing the data. It is done for the diagnosis of diseases by the radiologists and physicians. Noise corrupts the medical images and the quality of the images degrades. This degradation includes suppression of edges, structural details, blurring boundaries etc. To diagnose diseases edge and details preservation is very important. Medical image denoising can help the physicians or radiologists to diagnose the diseases. There are several techniques to suppress the noise. The main goal of denoising the medical images is to preserve the important feature such as edges, boundaries etc [14].
Image denoising is done by filtering which can be broadly divided into categories: linear filtering and nonlinear filtering. Mean filtering and Gaussian filtering are the example of spatial denoising methods. They are linear methods which cause blurring the images and simultaneously suppress the details. The performances of linear filters are not satisfactory because they blur the sharp edges; destroy lines and other finer details. To avoid these problems non-linear filtering is used. Bilateral filtering [15] is one of the examples of nonlinear filtering. It is a non-iterative method. It combines domain and range filters simultaneously. It preserves edge information while denoising. However it does not give satisfactory results, real gray levels are polluted seriously and the range filter cannot work properly. This phenomenon is called propagation of noise (PoN) [13].
Now a days ultrasound imaging is used widely in medical imaging because it is portable, relatively inexpensive and comparatively safe with other medical imaging techniques such as MRI and CT scan [5-9]. It is used to visualize muscles, their size, shape, injuries and soft tissues of the internal organs viz. liver, kidney, uterus, heart etc. Ultrasound images are severely affected by speckle noise [7, 8]. Unlike additive white Gaussian noise speckle noise is a type of multiplicative noise[21] which satisfies the condition:
w (x, y)=s(x, y) x n(x, y) (1)
where s(x, y) is the original signal, n(x,y) is the noise introduced into the original signal, w(x,y) is the corrupted image and (x, y) represents the pixel value of the image. Taking logarithm on both sides of (1) equation becomes:
log 10 w(x, y) =log 10 s(x, y) + log 10 n(x, y) (2)
In section II previous works for the image denoising using bilateral filter and other methods are discussed. Section III includes the introduction of bilateral filter. In Section III the notation of bilateral filter is to be formulized. Section IV presents the implementation of filter. In section V measurement of performance used in this paper to denoise the medical images is formulized. Section VI shows the experimental results and section VII includes conclusion and ideas for the further exploration in future.
-
II. II.LITERATURE REVIEW
Tomasi et al. (1998) proposed bilateral filtering for gray and color images. Bilateral filtering smoothes images while preserving edges, by means of a nonlinear combination of nearby image values. The method is non-iterative, local, and simple. It combines gray levels or colors based on both their geometric closeness and their photometric similarity and prefers near values to distant values in both domain and range. The performance of bilateral filter can be optimized if the noise level is known. Bilateral filter gives standard filtering performance for gray as well as color images. Also it does not produce phantom color along edges in
the color images and it reduces phantom colors if they appear in the image [10].
Michael Elad (2002) proposed a theoretical bridge and show that the bilateral filter also emerges from the Bayesian approach [16], using a novel penalty functional. For this functional, it is shown that a single iteration of the Jacobi algorithm yields the bilateral filter. Based on this observation, the bilateral filter can be improved to further speed-up its smoothing operation. Also, it is shown that the bilateral filter can be extended to treat more general reconstruction problems such as image restoration, image scaling, super-resolution etc.
Ming Zhang et al. (2008) proposed multi-resolution bilateral filter [17], where bilateral filtering is applied to the approximation (low-frequency) sub-bands of a signal decomposed using a wavelet filter bank. The multi-resolution bilateral filter is combined with wavelet thresholding [18].An image is decomposed into low and high frequency components and bilateral filter is applied on the approximate sub bands and wavelet thresholding on the detail sub bands. In the proposed method bayesshrink is used for wavelet thresholding technique. The performance can be improved by using redundant wavelet decomposition. This proposed method is the multiresolution application of bilateral filter.
Sudipta Roy et al. (2010) proposed a new model based on the hybridization of wavelet and bilateral filters for de-noising [1] of variety of noisy images. The performances are evaluated in terms of peak signal to noise ratio (PSNR) and image quality index (IQI). The use of bilateral filters in combination with wavelet thresholding [3] filters on sub-bands of a decomposed image deteriorates the performance. But the application of bilateral filter before and after decomposition enhances the performance. In addition, the proposed filter gives nearly uniform and consistent results on all the images.
Buyue Zhang et al. (2008) proposed the adaptive bilateral filter (ABF) for sharpness enhancement and noise removal [19]. The ABF sharpens an image by increasing the slope of the edges without producing overshoot or undershoot. It is an approach for the sharpness enhancement that is fundamentally different from the un-sharp mask (USM). This new approach to slope restoration also differs significantly from previous slope restoration algorithms in that the ABF does not involve detection of edges or their orientation, or extraction of edge profiles. In the ABF, the edge slope is enhanced by transforming the histogram via a range filter with adaptive offset and width. The ABF is able to smooth the noise, while enhancing edges and textures in the image. The parameters of the ABF are optimized with a training procedure. However the drawback of this filter is that it does not give better performance at corners as it gives on the lines and spatially slow-varying curves.
Lu Zhang et al. (2009) compared three kinds of representative medical image de-noising algorithms including anisotropic diffusion (AD) filtering; bilateral filtering and the sparse representation (SR) based method to provide convenience for targeted choosing of de-noising methods. The image de-noised by the sparse representation based method always has higher peak signal to noise ratio (PSNR) than that of the other methods but loses more details. Moreover sparse representation based method takes too long time to remove the noise while anisotropic diffusion filtering takes the shortest time. Although bilateral filter gives lower PSNR value than the sparse representation based method but it takes very less time than that of SR based method simultaneously it preserves more information which are lost by SR based denoising method [15].
Harold Phelippeau et al. (2008) proposed a method to automatically estimate the best intensity parameter set to remove the shot noise by considering automatic gain control (AGC) adjustment and the intensity mean and variance shot noise properties. The bilateral filter can be optimized if the noise level is known [12].
Francis et al. (2008) proposed an extension of the bilateral filter [20]. The proposed filter is a weighted median filter which adaptively estimates the weights in a similar manner to that of the bilateral filter. The proposed filter strikes a compromise between smoothing and preserving important detail.
Shyam Lal et al. (2011) proposed Complex Double Density Dual Tree Discrete Wavelet Transform for removing Additive Gaussian Noise. They highlighted wavelet based enhancement of gray scale digital images corrupted by additive Gaussian noise. The complex double density dual tree discrete wavelet transform outperforms in comparison with others wavelet transform in the highly corrupted images[3].
Liu Wei (2009) proposed a new method of denoising while keeping edge information [21]. In order to detect edges of the images while denoising; the image is divided into two parts. First edge parts and second smooth parts and accordingly thresholding is to be set. This method gives better response for edge preservation while denoising is done.
Alexander Wong (2008) proposed an adaptive bilateral filtering of image signals using local phase characteristics. This method uses the local phase characteristics of an image signal to perform bilateral filter in adaptive manner. This method is effective to remove noise signal along with the enhancement of perceptual quality [22].
Zhiwu Liao et al. (2010) proposed a method named context bilateral filter (CBF).In this method range filter is not defined on the gray level directly but it is defined on the context. Context is nothing but the smoother version of the image. If filter is applied on the context image; propagation of noise (PoN) is suppressed efficiently. The context bilateral filter gives good performance in the blind image denoising [13].
-
III. III. BILATERAL FILTERING
Bilateral filtering is a technique to smooth images while preserving edges. The use of bilateral filtering has grown rapidly and is now it is used in image processing applications such as image denoising, image enhancement etc[14]. Several qualities of bilateral filter are enlisted below which explains its success:
-
• It is simple to formulate it. Each pixel is replaced by a weighted average of its neighbors.
-
• It depends only on two parameters that indicate the size and contrast of the features to preserve.
-
• It is a non-iterative method. This makes the parameters easy to set since their effect is not cumulative over several iterations [13].
However, the bilateral filter is not parameter-free. The set of the bilateral filter parameters has an important influence on its behavior and performance. The parameters are window size w, standard deviation σ d and σ r . In the case of noise removal; the parameters have to be adapted to the noise level, while the bilateral filter adapts itself to the image details content.
The drawback of this filter is that it cannot remove salt and pepper noise [21] also it causes propagation of noise in medical images [13]. Another drawback of bilateral filter is that it is single resolution in nature that means it cannot access to the different frequency components of the image [1]. It is efficient to remove the noise in high frequency area but gives poor performance to remove noise to low frequency area.
-
IV. IV. IMPLEMENTATION OF BILETERAL
FILTER
Bilateral Filtering is achieved by the combinations of two Gaussian filters [15]. One filter works in spatial domain and second filter works in intensity domain. This filter applies spatially weighted averaging smoothing edges.
In traditional low pass filtering [13] it is assumed that the pixel of any point is similar to that of the nearby points:
h(x) = k a чхЖ ; «w (2)
where c (ξ,x) measures the geometric closeness between the neighborhood center x and a nearby point ξ.
Both input (f) and output (h) images may be multiband.
Also
∞
к» (x) = K_„ c(f,x)df (3)
But practically the pixel of points at boundaries is dissimilar to the nearby points. Therefore the boundaries are blurred. Bilateral filter combines gray levels based on both geometric closeness and photometric similarity and it prefers near values in both domain and range [13].
Range filtering is similarly defined:
h(x) = к; Чх)Д - тШ(з(КШ to)d ( (4)
where s (f (ξ), f(x)) measures the photographic similarity between the pixel at the neighborhood center x and that of nearby point ξ.
In this case, the kernel measures the photometric similarity between pixels. The normalization constant in this case is кг (x) = K2МШ(5)
We can combine equation (1) and (3) which describes the bilateral filtering as follows:
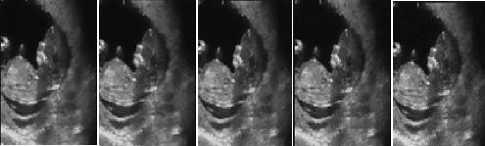
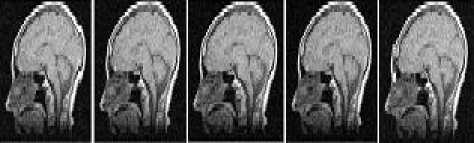
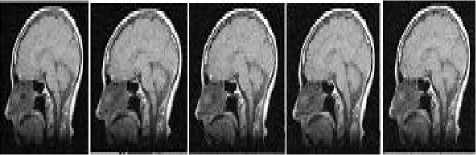
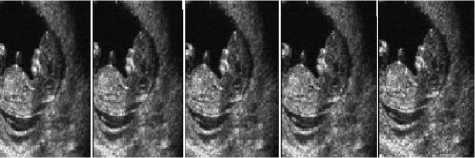
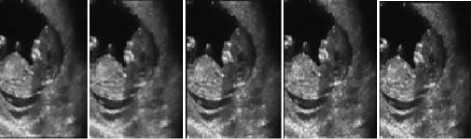
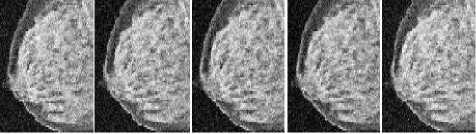
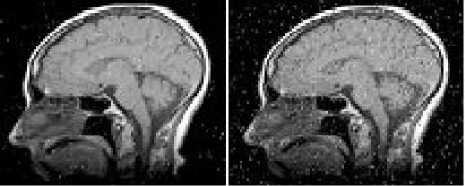
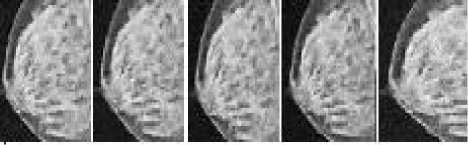
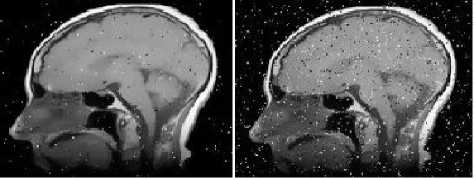
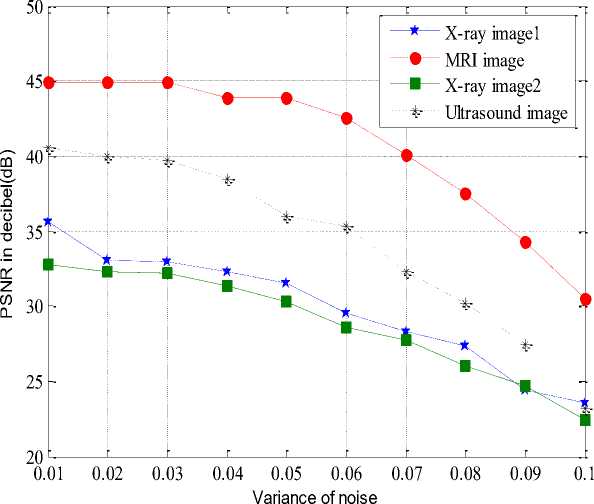
h(x) = к -1 (x) и; “f ( k(x) = JO( ^,x)f(f(^),f(x))d^ Combined domain and range filtering will be denoted as bilateral filtering [14]. It replaces the pixel value at x with an average of similar and nearby pixel values. In smooth regions, pixel values in a small neighborhood are similar to each other, and the bilateral filter acts essentially as a standard domain filter, averaging away the small, weakly correlated differences between pixel values caused by noise. Bilateral filtering is a noniterative method. Unlike traditional filters it removes the noise and preserves the edge information. But the optimal performance of the bilateral filter depends upon the parameters of the filter. V. V. MEASUREMENT OF PERFORMANCE To measure the performance of the denoising techniques several parameters are available for the comparison. Most common parameters are peak signal to noise ratio (PSNR), image quality index (IQI) and mean square error (MSE) etc [24].There are many other mathematical parameters using which the quality of denoised image can be calculated. In this paper peak signal to noise ratio is chosen as the performance parameter. The PSNR is defined as: PSNR (dB) =10 log10 (255 X 255)/MSE (8) where MSE is the mean square error between the denoised and original image[24]. It is calculated by taking the difference between two images pixel by pixel, square the result and final y average the results. Higher value of PSNR of denoised and original image implies that the performance of the denoising method is good. But it does not imply that the visual quality of the denoised image is good. VI. VI. EXPERIMENTAL RESULTS Bilateral filtering is applied in the different medical images such as x-ray images, MRI images and ultrasound images as shown below. In the first denoising experiment firstly different medical images are corrupted by additive white Gaussian noise (AWGN) with different values of variances σ2 from 0.01 to 0.1 then bilateral filtering is applied. The parameters of bilateral filter can be tuned to find the optimal performance. Those parameters are window size w, standard deviation σd and σr. These parameters control the behavior and performance of the bilateral filter. Figure shows the corrupted and filtered medical images. Figure1 and 3 are the x-ray images, figure 2 is MRI images and figure 4 is ultrasound images. Peak signal to noise ratio (PSNR) between filtered images and original image is shown in table.1.These images are obtained by applying Bilateral filtering technique with estimated filtering parameters viz. window size and standard deviation of the filter; in noisy medical images which are corrupted by additive white Gaussian noise(AWGN) with different values of variance from 0.01 to 0.1 Table.1 PEAK SIGNAL TO NOISE RATIO (PSNR) IN dB OF FILTERED IMAGES WITH ORIGINAL IMAGE WHICH ARE RESTORED BY BILATERAL FILTER AFTER CORRUPTING BY AWGN WITH CORRESPONDING VARIANCES. AWGN (σ2) Power Signal To Noise Ratio in dB x-ray 1 image MRI image x-ray 2 image US image 0.01 35.69 44.93 32.76 40.53 0.02 33.18 44.93 32.34 40.02 0.03 33.04 44.93 32.20 39.67 0.04 32.39 43.92 31.32 38.46 0.05 31.56 43.91 30.31 36.03 0.06 29.50 42.59 28.60 35.33 0.07 28.34 40.12 27.78 32.34 0.08 27.32 37.55 25.99 30.22 0.09 24.37 34.32 24.70 27.45 0.1 23.52 30.45 22.44 23.15 From this experiment it is clear that bilateral filter gives better performance to remove additive white Gaussian noise. It gives higher Signal to noise ratio (SNR) for image corrupted by AWGN than that of images which are corrupted by other noise signals. 1 ' 1 НИ4 т 1 1 * ' j fl j' i j1 J f I j (a) (b) (c) (d) (e) (a) (b) (c) (d) (e) Figure.1 X-ray image 1 corrupted by AWGN with variance (σ2) 0.01 to 0.05 respectively Figure.7 Ultrasound image corrupted by AWGN with variance (σ2) 0.01 to 0.05 respectively. **^^*^^*^^***^^*^^ '4'4' ' 1'4'4 (a) (b) (c) (d) (e) (a) (b) (c) (d) (e) Figure.2 Filtered image of figure 1 by bilateral filter. (a) (b) (c) (d) (e) Figure.3 MRI image corrupted by AWGN with variance (σ2) 0.01 to 0.05 respectively. (a) (b) (c) (d) (e) Figure.8 filtered image of figure 7 by bilateral filter. (a) (b) (c) (d) (e) Figure.9 Ultrasound image corrupted by speckle noise with variance (σ2) 0.01 to 0.05 respectively. (a) (b) (c) (d) (e) Figure.4 filtered image of figure 3by bilateral filter. (a) (b) (c) (d) (e) Figure.5 X-ray image 2 corrupted by AWGN with variance (σ2) 0.01 to 0.05 respectively. Figure.10 filtered image of figure 9 by bilateral filter. (a) (b) (a) (b) (c) (d) (e) Figure.6 filtered image of figure 5 by bilateral filter. (a) (b) Figure.12 image 11 restored by bilateral filter. Now in the second denoising experiment ultrasound image is corrupted by speckle noise with different values of variances σ2 from 0.01 to 0.05 then bilateral filtering is applied. The parameters of bilateral filter are tuned to get optimal performance. Figure 9 shows the noisy images which are corrupted by speckle noise with different values of variance from 0.01 to 0.05. Figure 10 are the filtered images of figure 9. Peak signal to noise ratio (PSNR) between filtered images and original image is calculated and listed in table.2. From this calculation it can be said that performance of bilateral filter is not satisfactory to remove speckle noise. Table.2 PEAK SIGNAL TO NOISE RATIO (PSNR) IN dB OF FILTERED IMAGES WITH ORIGINAL IMAGE WHICH ARE RESTORED BY BILATERAL FILTER AFTER CORRUPTING BY SPECKLE NOISE WITH CORRESPONDING VARIANCES. Variance 0.01 0.02 0.03 0.04 0.05 PSNR(dB) 19.94 18.85 18.16 17.53 16.27 Graph between PSNR (dB) and variance is plotted as shown in figure 13 for experiment 1 in which firstly medical images are corrupted by additive white Gaussian noise and then restored by using bilateral filter. VII. CONCLUSION & FUTURE SCOPE OF WORK We have presented the bilateral filter to denoise the medical images. Its performance is better than that of linear filters such as Wiener filter, mean filters etc. It gives better performance to remove the noise in high frequency area but it fails to remove noise to low frequency area. However its performance is not satisfactory to remove the noise from the image. The drawback of this filter is that it cannot remove salt and pepper noise. Also it gives poor performance to remove speckle noise from the ultrasound images. To improve the response of bilateral filter to remove speckle noise; multiplicative noise modal can be transferred into an additive one by taking logarithm of the corrupted image. This is a non-iterative method. This filter is not free from parameters. The performance of bilateral filter depends upon the parameters viz. window size (w) and standard deviations (σd , σr). We applied it on medical images such as x-ray image MRI image and ultrasound image which are corrupted by AWGN with different values of variance. We can say that the success of the bilateral filter lies in its combination of simplicity, good results and efficient algorithms. Although there are many alternative methods available for each of this points but only few of them gives all these advantages simultaneously. The original goal of the filter is denoising; in which case a small spatial kernel suffices and the residual of the filter is discarded as the noise component. In contrast, many new applications leverage the bilateral filter to create two-scale decompositions that rely on large spatial kernels and where the residual of the filter is preserved because it is much more relevant to the human visual system. In this paper bilateral filtering is used for denoising the medical images. It is better than many techniques. Simultaneously it can be for different other applications such as contrast management, detail enhancement, depth reconstruction, data fusion, 3D fairing, texture and illumination separation, tone mapping, retinex, and tone management, orientation smoothing etc. Bilateral filtering can be used for processing video signals also. [1] Sudipta Roy, Nidhi Sinha, Asoke K. Sen. A New Hybrid Image Denoising Method. International Journal of Information Technology and Knowledge Management, 2010, 2(2) :491-497. [2] Rafael C. Gonzalez, Richard E. Woods,Digital Image processing using MATLAB. Second Edition, Mc Graw hill. [3] Shyam Lal, Mahesh Chandra, Gopal Krishna Upadhyay, Deep Gupta. Removal of Additive Gaussian Noise by Complex Double Density Dual Tree Discrete Wavelet Transform. MIT International Journal of Electronics and Communication Engineering , 2011, 1(1):8-16. [4] H. Guo, J. E. Odegard, M.Lang, A. Gopinath, J. W. Selesnick. Wavelet based Speckle Reduction with Application to SAR based ATD/R. First International Conference on Image Processing 1994:75-79. [5] S.Kalaivani Narayanan, and R.S.D.Wahidabanu. A View on Despeckling in Ultrasound Imaging. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2009, 2(3):85-98. [6] Manish Goyal, Gianetan Singh Sekhon. Hybrid Threshold Technique for Speckle Noise Reduction using wavelets for Grey scale images. IJCST, 2011, 2(2) :620-625. [7] S.Sudha, G. R. Suresh, R. Suknesh. Speckle Noise Reduction in Ultrasound Images by Wavelet Thresholding based on Weighted Variance. International Journal of Computer Theory and Engineering,2009, 1(1):7-12. [8] T. Ratha Jeyalakshmi, K. Ramar. A Modified Method for Speckle Noise Removal in Ultrasound Medical Images. International Journal of Computer and Electrical Engineering, 2010,2(1):54-58. [9] Takanori Koga, Eiji Uchino, Noriaki Suetake, Genta Hashimoto, Takafumi Hiro, Masunori Matsuzaki. Speckle Noise Reduction and EdgeEnhancement of Coronary Plaque Tissue in Intravascular Ultrasound Image by Using Anisotropic Diffusion Filter. International Journal of Circuits, System and Signal processing, 2008, 4(2):239-248. [10] Pei-Yin Chen. An Efficient Edge-Preserving Algorithm for Removal of Salt-and-Pepper Noise. IEEE Signal processing letter, 2008, 15:833-836. [11] Robert D. Nowak. Wavelet Based Rician Noise Removal. IEEE Transactions on Image Processing, 1999, 8(10) :1408-1419. [12] Harold Phelippeau. Shot Noise Adaptive Bilateral Filter. IEEE Signal Processing, ICSP 2008, 9th International Conference, 2008:864 – 867. [13] Zhiwu Liao,Shaoxiang Hu,Zhiqiang Yu,Dan Sun. Medical Image Blind Denoising Using Context Bilteteral Filter. International Conference of Medical Image Analysis and Clinical Application, 2010:12-17. [14] C.Tomasi, R. Manduchi. Bilateral Filtering for Gray and Color images. Procedings of IEEE international Conference on Computer Vision, Bombay, India, 1998: 839-846. [15] Lu Zhang, Jiaming Chen, Yuemin Zhu, Jianhua Luo. Comparisons of Several New Denoising Methods for Medical Images. IEEE, 2009:1-4. [16] Michael Elad. On the Origin of the Bilateral Filter and Ways to Improve It. IEEE transaction on image processing, 2002, 11(10):1141-1151. [17] Ming Zhang, Bahadir K. Gunturk. Multiresolution Bilateral Filtering for Image Denoising. IEEE transaction on image processing, 2008, 17(12):2324-2333. [18] S.Kother Mohideen, S. Arumuga Perumal, M.Mohamad Sathik. Image De-noising using Discrete Wavelet transform. IJCSNS International Journal of Computer Science and Network Security, 2008, 8(1):213-216. [19] Buyue Zhang. Adaptive Bilateral Filter for Sharpness Enhancement and Noise Removal. IEEE transaction on image processing, 2008, 17(5):664-678. [20] J.J. Francis, G. de Jager. “The Bilateral Median Filter” IEEE Transactions on Image Processing, 2008:421–432. [21] Liu Wei. New Method for Image Denoising while Keeping Edge Information. Image and Signal Processing, CISP 09. 2nd International Congress, 2009:1-5. [22] Alexander Wong. Adaptive bilateral filtering of image signals using local phase characteristic. Elsevier, Signal Processing, 2008, 88:1615-1619. Devanand Bhonsle, male, is a Sr. Assistant Professor at Shri Shankaracharya Technical Campus, Bhilai, India. He is currently working toward the Ph.D. degree in the Electronics & Telecommunication from Chhattisgarh Swami Vivekanand University, Bhilai, India. His research interests include computer vision, digital image processing and Software Development. His teaching interests include digital image processing, digital electronics and analog electronics. G.R. Sinha, male, is Professor & Associate Director at Shri Shankaracharya Technical campus, Bhilai, India. His research interests include digital image processing and applications in biometrics, medical image processing and diagnosis. He has authored two books on wavelet based PCG signal analysis and Adhoc networks.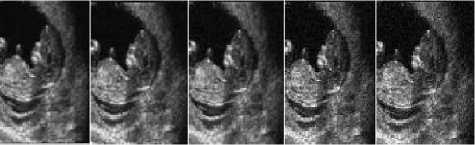
Список литературы Medical Image Denoising Using Bilateral Filter
- Sudipta Roy, Nidhi Sinha, Asoke K. Sen. A New Hybrid Image Denoising Method. International Journal of Information Technology and Knowledge Management, 2010, 2(2) :491-497.
- Rafael C. Gonzalez, Richard E. Woods,Digital Image processing using MATLAB. Second Edition, Mc Graw hill.
- Shyam Lal, Mahesh Chandra, Gopal Krishna Upadhyay, Deep Gupta. Removal of Additive Gaussian Noise by Complex Double Density Dual Tree Discrete Wavelet Transform. MIT International Journal of Electronics and Communication Engineering , 2011, 1(1):8-16.
- H. Guo, J. E. Odegard, M.Lang, A. Gopinath, J. W. Selesnick. Wavelet based Speckle Reduction with Application to SAR based ATD/R. First International Conference on Image Processing 1994:75-79.
- S.Kalaivani Narayanan, and R.S.D.Wahidabanu. A View on Despeckling in Ultrasound Imaging. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2009, 2(3):85-98.
- Manish Goyal, Gianetan Singh Sekhon. Hybrid Threshold Technique for Speckle Noise Reduction using wavelets for Grey scale images. IJCST, 2011, 2(2) :620-625.
- S.Sudha, G. R. Suresh, R. Suknesh. Speckle Noise Reduction in Ultrasound Images by Wavelet Thresholding based on Weighted Variance. International Journal of Computer Theory and Engineering,2009, 1(1):7-12.
- T. Ratha Jeyalakshmi, K. Ramar. A Modified Method for Speckle Noise Removal in Ultrasound Medical Images. International Journal of Computer and Electrical Engineering, 2010,2(1):54-58.
- Takanori Koga, Eiji Uchino, Noriaki Suetake, Genta Hashimoto, Takafumi Hiro, Masunori Matsuzaki. Speckle Noise Reduction and Edge-Enhancement of Coronary Plaque Tissue in Intravascular Ultrasound Image by Using Anisotropic Diffusion Filter. International Journal of Circuits, System and Signal processing, 2008, 4(2):239-248.
- Pei-Yin Chen. An Efficient Edge-Preserving Algorithm for Removal of Salt-and-Pepper Noise. IEEE Signal processing letter, 2008, 15:833-836.
- Robert D. Nowak. Wavelet Based Rician Noise Removal. IEEE Transactions on Image Processing, 1999, 8(10) :1408-1419.
- Harold Phelippeau. Shot Noise Adaptive Bilateral Filter. IEEE Signal Processing, ICSP 2008, 9th International Conference, 2008:864 – 867.
- Zhiwu Liao,Shaoxiang Hu,Zhiqiang Yu,Dan Sun. Medical Image Blind Denoising Using Context Bilteteral Filter. International Conference of Medical Image Analysis and Clinical Application, 2010:12-17.
- C.Tomasi, R. Manduchi. Bilateral Filtering for Gray and Color images. Procedings of IEEE international Conference on Computer Vision, Bombay, India, 1998: 839-846.
- Lu Zhang, Jiaming Chen, Yuemin Zhu, Jianhua Luo. Comparisons of Several New Denoising Methods for Medical Images. IEEE, 2009:1-4.
- Michael Elad. On the Origin of the Bilateral Filter and Ways to Improve It. IEEE transaction on image processing, 2002, 11(10):1141-1151.
- Ming Zhang, Bahadir K. Gunturk. Multiresolution Bilateral Filtering for Image Denoising. IEEE transaction on image processing, 2008, 17(12):2324-2333.
- S.Kother Mohideen, S. Arumuga Perumal, M.Mohamad Sathik. Image De-noising using Discrete Wavelet transform. IJCSNS International Journal of Computer Science and Network Security, 2008, 8(1):213-216.
- Buyue Zhang. Adaptive Bilateral Filter for Sharpness Enhancement and Noise Removal. IEEE transaction on image processing, 2008, 17(5):664-678.
- J.J. Francis, G. de Jager. “The Bilateral Median Filter” IEEE Transactions on Image Processing, 2008:421–432.
- Liu Wei. New Method for Image Denoising while Keeping Edge Information. Image and Signal Processing, CISP 09. 2nd International Congress, 2009:1-5.
- Alexander Wong. Adaptive bilateral filtering of image signals using local phase characteristic. Elsevier, Signal Processing, 2008, 88:1615-1619.


