Механическая аналогия длинного джозефсоновского перехода

Работа ряда электротехнических устройств микромеханики в аэрокосмической отрасли основана на использовании для конструирования этих сложных приборов некоторых нелинейных свойств различных неоднородных структур. Свойства неоднородных структур определяются как собственными характеристиками материала, так и размерными параметрами конкретного образца. Типичным примером такого соотношения свойств являются слоистые материалы, свойства которых во многом определяются условиями на границе раздела слоев, т. е. их граничными условиями. Именно от этих граничных условий во многом и зависят размерные и частотные эффекты.

Одним из известных и часто используемых размерных эффектов является Эйлерова неустойчивость при изгибе стержня конечной длины под действием продольной силы. Для величины этой силы находится спектр собственных значений, каждому из которых соответствует своя искривленная форма стержня. Долгое время способы достижения форм искривления, соответствующих второму и последующему собственному значению спектра, не были известны. В основополагающей работе М. А. Лаврентьева и А. Ю. Ишлинского [1] было показано, что достижение форм искривления стержня, соответствующих второй и следующим модам, возможно путем взрывного, динамического нагружения. Первый порог был назван ими статическим порогом потери устойчивости, а пороги, следующие за первым - динамическими порогами потери устойчивости.

В работе [2] было показано, что задача о перемагничивании тонкого ферромагнитного слоя с намагниченностью, закрепленной на одной поверхности и свободной на другой под действием магнитного поля, аналогична классической Эйлеровой задаче об изгибе тонкого стержня. Таким образом, было показано, что потеря устойчивости при внешнем воздействии характерна не только для упругих систем, но и систем для более широкого круга.

Джозефсоновский переход является слоистой структурой, характеристики которой описываются уравнениями, аналогичными уравнениям для некоторых упругих и магнитных систем. Поэтому попытаемся рассмотреть процессы в длинном джозефсоновском переходе как аналогию устойчивости Эйлерова стержня при продольном воздействии сжимающей силы.

Ранее в работе [3] было показано, что электродинамика протяженного джозефсоновского контакта для разности фаз ф волновых функций сверхпроводников, обра зующих контакт, описывается дифференциальным уравнением в частных производных, которое при отсутствии диссипативного члена имеет вид

1 ∂ ² ϕ     1

^4ф»^-   м%^{sm ф} •         ⁽¹⁾

где c = с (1 /4 п Cd) ^1/2 - скорость распространения вдоль поверхности туннельного перехода электромагнитных волн; %=( Й /2^ ₀ edJ_c ) ^1/2 -джозефсоновская глубина проникновения, т. е. ширина области по краям контакта, в которой протекают джозефсоновские токи. Здесь J - джозефсоновский критический ток, С - емкость контакта, приходящаяся на единицу площади, d - толщина области контакта, в которую проникает магнитное поле.

При этом плотность тока J , протекающего через переход, определяется уравнением [4]

J= J _c sin ф.

В свою очередь магнитного поле перехода связано с разностью фаз выражением [5]

π ed

Уф=     [ H х n ] .

h

В стационарном случае, когда разность фаз ф не зависит от времени t, уравнение (1) переходит в уравнение нелинейного маятника

^А Ф - , y = TT^sm Ф.                 (4)

λ _J

Решение данного нелинейного уравнения хорошо известно, и в случае определенных граничных условий приводит к появлению спектра собственных значений, что было показано К. С. Оуэном и Д. Дж. Скалапино [6]. Однако найденный ими спектр решений был связан с усло вием периодичности и получил геометрическое толкование как кратность глубины проникновения %J и размера перехода L, описываемое соотношением

L-2 п % _Jk l K< к ² ), (5) где К - полный эллиптический интеграл первого рода с модулем к .

Вместе с тем при проведении аналогии между магнитной и упругой системой было показано, что получаемый в таких задачах спектр собственных значений определяет последовательность порогов потери устойчивости системы, при которых нарушается симметрия состояния системы [2]. При этом значение для первого порога потери устойчивости, связанного со спонтанным нарушением симметрии, не нашло своего отображения в работе И. О. Кулика [7].

В связи с вышеизложенным возникает необходимость более подробного изучения решений уравнения (4). Для этого рассмотрим джозефсоновский контакт простейшей геометрии (рис. 1).

Н е

Н

d

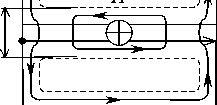
Рис. 1. Одномерный джозефсоновский переход с симметричной линейной геометрией [4]

Н е

Распределение разности фаз волновых функций сверхпроводников, образующих контакт вдоль перехода, описывается уравнением d Ф

— = —sin ф dx kJ с граничными условиями [7]

d ф^ _ He dx )x_0 HоL ’ V dx

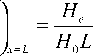
где Н3£ = Ф0/2лd, здесь Фо- квант магнитного потока, d - толщина области контакта, в которую проникает магнитное поле. Для удобства введем обозначение k7=1о^с,                    (8)

где ! . - Ф _о / L ₀ - минимальный ток [4], создающий в переходе с индуктивностью L ₀ - 2лц _о d квант магнитного потока Ф _о . Тогда величина Н ₀ L связана с индуктивностью соотношением Н ₀ L - Ф _о ^ ₀ / L ₀ -! ₀ ц ₀ .

Уравнение (4), как мы уже отмечали выше, - это уравнение нелинейного маятника, общее решение которого записывается с помощью эллиптических функций Якоби и эллиптических интегралов с модулем к , который определяется плотностью тока, протекающего через переход [6]:

ф-л + 2 ат [ х/к k ₄ +F ₁₂ , к ],             (9)

где F ₁₂ - константа интегрирования,

F ₁₂ - F [arcsin ( к " ¹ ^ 1 - ( k k J H e /2 H ₀ L ) ² ), к ], (10) здесь F - эллиптический интеграл первого рода.

Как было показано в работе [3], случаю когда к< 1, соответствует ситуация, когда внешнее магнитное поле больше собственного магнитного поля перехода. Соответственно когда внешнее магнитное поле меньше собственного магнитного поля, модуль к> 1. Сделав замену к"1 = к*, получим ф-n + 2arcsin {к* sn[х/ky+F11, к*]},       (11)

где F ₁₁ - F [arccos(kД / Д 2 к * Н ₀ L ), к * ] - константа интегрирования.

Поскольку, как было сказано выше, полученное в [6] решение было связано с условием периодичности и получило геометрическое толкование, мы можем рассмотреть процессы в длинном джозефсоновском переходе как Эйлерову неустойчивость при воздействии на переход внешнего магнитного поля.

По аналогии с Эйлеровой силой для упругого стержня Р, - (п / 2) ² Е1/L ² , введем критическое значение плотности тока, соответствующее первому статическому порогу:

J ₁ -4п ² 7 о / L ² ,                   (12)

где L - продольный размер одномерного перехода. Соответственно первое критическое значение магнитного поля

Н ₁ -4п Н _о .                  (13)

Анализ выражения (12) показывает, что первое критическое значение плотности тока J ₁ есть такая минимальная плотность тока ! _о , который должен протекать через переход, чтобы при его соответствующих геометрических размерах [4] в нем возник квант магнитного потока Ф _о , т. е. такая плотность тока, при которой происход переходит из мейснеровского состояния в смешанное и в этот переход проникают кванты магнитного потока, нарушая симметрию системы. Аналогично в упругом стержне исходной является однородная, не искривленная форма, и потеря устойчивости состоит в появлении определенной моды искривления. Не трудно заметить, что плотность тока ! _о соответствует жесткости упругого стержня - произведению модуля Юнга Е на момент инерции ! сечения стержня.

Как отмечалось ранее, решение таких граничных задач приводит к появлению спектра собственных решений. Учитывая введенное нами первое значение критической плотности тока (12) и выражение для магнитного поля (13), получим спектр собственных значений для случаев, когда магнитное поле больше или меньше собственного магнитного поля. С этой целью рассмотрим два случая: собственное поле перехода больше внешнего магнитного поля; собственное поле перехода меньше внешнего магнитного поля.

В случае когда собственное поле перехода больше внешнего магнитного поля, распределение разности фаз вдоль перехода определяется выражением (11). Тогда, используя граничные условия (7) и учитывая периодичность эллиптических функций, найдем

J _ 4 mK ( к *) X Ч L

,т- 1,2, ....

Применяя формулу (12), получим выражение для определения зависимости к * от плотности тока J :

J ⁽ m ) _ J 1 ( 2/ п ) ² [ mK ( к *) ] 2 .           (15)

Отсюда величина порогов потери устойчивости для к * -0

J h ) _ m ² J , , ^ -1,2,.. (16)

Поскольку внешней силой является магнитное поле, выражение для определения зависимости к * от внешнего магнитного поля будет иметь вид

H^{( m} ) _ H 1- mK ( k ) . (17) п

Соответственно для пороговых значений поля

H h ) _ mH 1 , ^ -1, 2,..., (18) отсюда можно сделать вывод, что для джозефсоновского перехода неустойчивость состоит в появлении следующего кванта магнитного потока.

Теперь, зная зависимость (15) модуля к ‘ от плотности тока J , найдем выражение для пространственного распределения плотности тока вдоль перехода, учитывающее пороговый характер поведения плотности тока и магнитного поля в переходе:

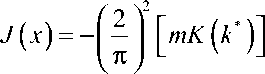
k *2 J 1sn ( 4 mK ( k *) L + F 11 , k*

x dn ⁽ 4 mK ( k *) L + F_u, k * ^j           (19)

Соответственно для магнитного поля на основе формул (17)и (3) получим пространственную зависимость распределения поля вдоль перехода:

H (x) = 4mK (k*) k * H0 cn ( 4mK (k*) x + F11, k* j. (20) В случае когда собственное поле перехода меньше внешнего поля магнитного поля и пространственное распределение разности фаз определяется выражением (9) и граничными условиями (7), аналогично найдем

J Г 2 mkK ( k ) '

, т = 1,2,

Используя первое критическое значение плотности тока (12), получим уравнение для определения зависимости модуля к от плотности тока J _m :

J = ( 1/п ) ² Г mkK ( k ) ] ² J 1 .            (22)

Аналогично для магнитного поля

H = H 1- mkK ( k ) .          (23)

п

Поскольку в данном случае магнитное поле больше собственного магнитного поля перехода, то по выражению (23) следует, что модуль к не может принимать произвольные значения. Область определения модуля к найдем подставив выражения (23) и (21) в (10): F ₁₂ = F [arcsin( к ‘ / к ), к ], где к ‘ - дополнительный модуль ( к ² + к ^,2 = 1). В этом случае область определения к имеет вид S J к ² J 1.

По выражению (22) при к ² = 1/2 найдем величины порогов потери устойчивости:

J^m) = З2 m2 J1 ,т = 1,2,_,(24)

где

З2 = K2 (V2/2у2п2 = 0,174.(25)

Для пороговых значений поля при к ² = 1/2 получим

Hm) = ЗmH1 ,т=1,2, _.(26)

При J ^ J ₁ модуль к ² ^ 1/2; в случае когдаJ> J ₁ , к ² > 1/2. Отметим, что выражения (15) и (22) для модуля к * и к идентичны друг другу, за исключением того, что к явно входит в уравнение (22) для зависимости J _m .

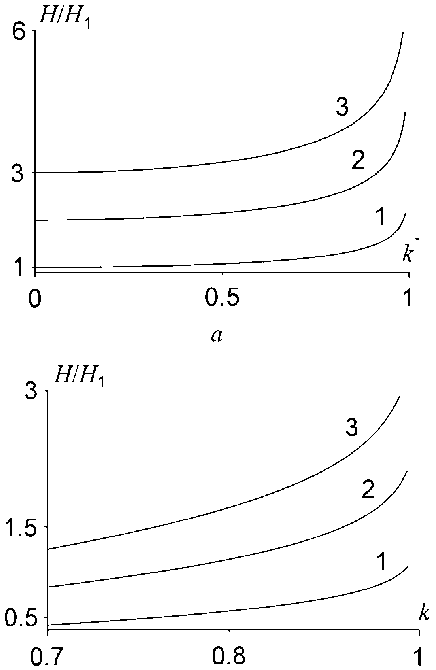
Зависимости магнитного поля от модуля к и к * (рис. 2) имеют сходство с зависимостями внешней сжимающей силы Р от модуля к для упругого стержня.

Используя выражения (22) и (23), получим для случая когда собственное поле перехода меньше внешнего магнитного поля, зависимость распределений плотности тока и магнитного поля вдоль перехода:

. .    ( 1 Yr . ,.„2      (      ,.,x      Л

J ( x ) = -1     Г mkK ( k ) ] 2 J 1snI 2 mK ( k )— + F ₁₂, k x

VⁿJ                  I ^L ) (27)

x cn ⁽ 2 mK ( k ) L + F ₁₂, k ^j

H ( x ) = 4 mK ( k ) H ₀dn ⁽ 2 mK ( k ) L + F ₁₂, k ^j . (28)

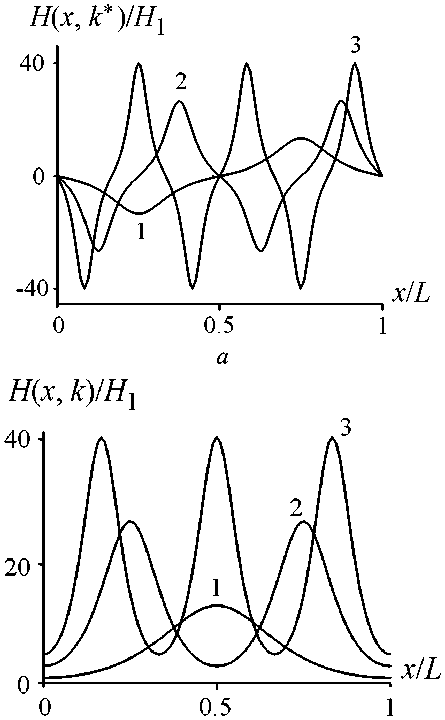
Анализ распределений магнитного поля в джозефсо- новском переходе (рис. 3) показывает, что поведение про никающих в переход вихрей магнитного потока подобно поведению одномерной цепочке спинов во внешнем магнитном поле.

б

Рис. 2. Зависимость магнитного поля от модуля к для разных порогов: 1 - статического ( т = 1);

2 и 3 - динамических ( т = 2 и т = 3); а - внутреннее поле перехода больше внешнего поля; б - внутреннее поле

перехода меньше внешнего поля

б

Рис. 3. Распределение магнитного поля вдоль перехода по координате х для разных порогов: 1 - статического ( т = 1);

2 и 3 - динамических ( т = 2 и т = 3); а - внутреннее поле перехода больше внешнего поля; б - внутреннее поле меньше внешнего поля при одинаковом модуле, равном 0,99

В случае когда внешнее магнитное поле меньше собственного поля перехода, упорядочение вихрей происходит антипараллельно, т е. вихри, проникающие в переход, образуют структуру «вихрь-антивихрь» (рис. 3, а ), такое упорядочение соответствует антиферромагнитному способу упорядочения цепочки спинов. В противоположном случае упорядочение происходит параллельным способом (рис. 3, б ): вектор напряженности поля проникающих вихрей направлен в одну сторону, что соответствует ферромагнитному упорядочению спинов. Таким образом, можно сказать, что в длинном джозеф-соновском переходе возникает своего рода динамическая доменная структура. Учитывая проведенную аналогию между длинным джозефсоновским переходом и упругим стержнем, рассмотрим процесс взаимодействия внешнего магнитного поля с переходом.

В случае когда внешнее магнитное поле равно нулю и постепенно увеличивается, мы имеем мейснеровское распределение поля в переходе, описанное в работах [3; 6; 7].

В случае резкого, импульсного увеличения внешнего поля до некоторой критической величины переход, подобно упругому стержню, будет терять устойчивость из-за того, что в переход проникнут кванты магнитного потока, упорядочение которых будет происходить антиферромагнитным способом, т. е. возникнет своего рода динамическая доменная структура. Дальнейшее поведение системы зависит от величины приложенного внешнего поля. В частности, при релаксации системы может произойти упорядочение вихрей по полю, или намагничивание динамической доменной структуры. Но этот процесс представленными в данной статье уравнениями не описывается.

В другом случае, когда начальное состояние длинного джозефсоновского перехода отлично от рассмотренного выше, при импульсном воздействии на него внешнего магнитного поля также будет происходить потеря устойчивости, связанная с проникновением в переход вихрей магнитного поля. Однако в этом случае в связи с тем, что начальное состояние не является собственным состоянием системы, а является наведенным, то пороги потери устойчивости появятся при отличном от нуля значении модуля к , а упорядочение проникающих вихрей в переход будет происходить ферромагнитным способом.

В заключение можно сделать вывод, что в рассмотренных в данной статье сверхпроводящей, магнитной и упругой системах происходит характерная потеря устойчивости при внешнем воздействии на систему Потеря устойчивости приводит к нарушению симметрии в системе, и для длинного джозефсоновского перехода она связана с проникновением в него вихрей магнитного поля. Полученные решения показывают непосредственную связь между величиной внешнего магнитного поля и числом вихрей проникающих в переход. В свою очередь, упорядочение проникших в переход вихрей происходит подобно динамической доменной структуре. Все отмеченное выше позволяет использовать джозефсонов-ский переход при конструировании вычислительных систем как элемент нечеткой логики и устройств микромеханики.

Работа выполнена при поддержке ведомственной научной программы «Развитие научного потенциала высшей школы», проект № 4418.