Механические характеристики электромагнитных демпфирующих элементов с двойным ротором

Электромагнитные демпфирующие элементы (ЭДЭ), вторичная среда которых выполнена в виде двойного ротора, отличаются высокой эффективностью, широким диапазоном рабочих скоростей и широкими возможностями управления процессом торможения благодаря специальной механической характеристике.

Интересным представляется рассмотрение задачи исследования механических характеристик двухроторных ЭДЭ (ДЭДЭ) в установившемся режиме. При проектировании ЭДЭ для амортизационных систем исходя из статических механических характеристик стремятся получить максимальный электромагнитный момент при заданной скорости вращения и выбранных габаритах демпфера, а для демпферов, используемых в качестве нагрузочных элементов автоматизированных испытательных стендов, установившийся режим является основным.

В [1] получены механические характеристики для ДЭДЭ при встречном движении роторов, что на практике трудно реализуемо. В данной статье разрабатывается математическая модель, с использованием уравнений электромагнитного поля, позволяющая получать механические характеристики ДЭДЭ, роторы которого движутся согласованно. При построении модели использованы общепринятые при теоретическом исследовании ЭДЭ допущения [7].

На рис. 1 представлен эскиз ДЭДЭ, с полыми цилиндрическими роторами из немагнитных про водящих материалов. В такой конструкции отсутствует продольный краевой эффект, поперечный краевой эффект может быть учтен введением поправочного коэффициента [6].

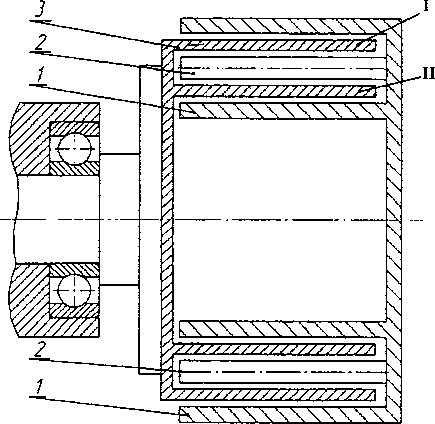
Рис. 1. Эскиз электромеханического демпфирующего элемента с двойным ротором: 1 - статор; 2 - индуктор с постоянными магнитами; 3 - двойной полый ротор

При таком конструктивном исполнении электромагнитный момент ДЭДЭ можно определить как сумму моментов от каждого ротора

М = М_Х+М₂,                     (1)

где М_х и М₂ - моменты, создаваемые внешним (I) и внутренним (II) роторами.

Электромагнитный момент может быть определен отдельно для каждого ротора через результирующую индукцию магнитного поля и плотность тока, наводимого в соответствующем роторе [2 5].

В рассматриваемом ЭДЭ (см. рис. 1) скорость имеет одну составляющую по оси х VX=V ; Ц = 0; V. = 0 . При принятых допущениях векторы индукции и напряженности магнитного поля имеют только составляющую по оси z : В.= В ; Н. = Н , а плотности вихревых токов будут иметь одну составляющую 8^ и 82у. Так как напряженность первичного магнитного поля изменяется по гармоническому закону вдоль оси х, то комплексные амплитуды векторов напряженностей вторичных магнитных полей в установившемся режиме также будут изменяться по гармоническому закону[2-5]. Тогда выражения для моментов можно записать в комплексной форме л£>, 2а А]_

М_х = —- Re j J ^b_XyBdxdydz;

ООО ti)2 2а Д2 __

М2=~Re J J ^b2yBdxdydz,(2)

где В - сопряженное значение результирующей индукции магнитного поля; А,, Д₂ - толщина полого I и II ротора соответственно; 2а - ширина магнитной системы; Д и У₂ - средние диаметры первого и второго роторов соответственно.

Целесообразно представить выражения для электромагнитных моментов I и II роторов в следующем виде:

Мх = МБ • тх;

М₂=М_Б-т₂,                    (3)

где М_Б - базовая величина электродинамического момента; т_х, т₂ - относительный электродинамический момент в I и II зоне.

В качестве базовой величины принимается максимальный электромагнитный момент первого ротора м                                 (4)

4Ц0^1

где В_От - амплитуда индукции первичного магнитного поля; ц₀ - магнитная проницаемость.

Учитывая то, что поле постоянных магнитов является безвихревым rot Е = 0, а индукции и напряженности связаны соотношением:

Д = n₀K_dxH_x;

Д ⁼ V^xoK_d2H₂,                            (5)

где K_dX, K_d2 - коэффициенты приведения для зон I и II [1-4], результирующее магнитное поле можно представить в виде суммы первичного и вторичных полей

Н = Н0+Нх+Н2;

В = Bq + В_х + IE ,

где Н , В - напряженность и индукция результирующего магнитного поля; Но, Во - напряжен ность и индукция первичного электромагнитного поля; Нх, Вх - напряженность и индукция вто ричного электромагнитного поля, создаваемого токами I ротора; Н2, В2 - напряженность и ин дукция вторичного электромагнитного поля, создаваемого токами II ротора.

На основе уравнений Максвелла в одномерном приближении можно получить следующие уравнения для определения напряженностей вто ричных магнитных полей

Н_х =    f Я + Я₂^- + —) ;

1   7 \ 1   2 Kdx ^Kdx)

Н2 =           +

(  ^2 Но^2

у     _ C2^0^d2 у где е, ---ла1, е2 ---ла2 - а,                   а2

безразмерные частоты, характеризующие интенсивность электромагнитных процессов (магнитное число Рейнольдса) в зонах I, II; КаХ, Кс2 - коэффициенты уменьшения электрической проводимости, учитывающие проявление поперечного крае вого эффекта по [6]; СХ] = — ; а2 =—; т,, т2 -Т]         т2

полюсные деления для I и II зон.

Решение (7) дает выражения для напряженностей магнитного поля

Ро^1^ + (е1 +s2) ]   Ро^1[1 + (Е1 +е2) ]

Д₎е₂(Е₁+Б₂)                Bq^          ₍,

Po-^/2[l+(ei+ез)2] Мо'^/г^+Ч+ег)2]

Плотности вихревых токов

^ = —т- = 7«1Я1;

5₂ =— -^ = ja₂H₂.                (9)

Эх

Результирующие индукции магнитных полей обоих зон равны и определяются следующим образом:

^вр=; , °          °; ¹              (10)

1 +    4- Ел )      1 + [Sj 4" Е2 у

Тогда используя (2) с учетом (3) и (4), относи тельные электромагнитные моменты определяют ся по выражениям:

ских проводимостей роторов, физических свойств материалов магнитопровода, а также геометрии магнитной системы. Максимальное значение суммарного момента запишется в виде

1 + (S| + Е2 j

K*_d 2е₂

^д^т l + (sj+E2)2

(И)

где K_d - —— , ^(/2        ^Д2

«2 «1

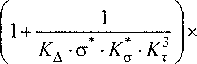
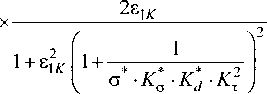
Линейные скорости роторов в I и II зоне И и Из прямо пропорциональны угловой частоте вращения и. Это также справедливо и для безраз мерных величин £[ и е2, что позволяет устано вить неразрывную связь между ними, которая может быть записана в виде

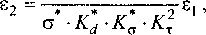
^С2 ^с2

Выражения (12) позволяют исследовать влияние электромагнитных процессов в одном роторе на аналогичные в другом. Это влияние оказывается размагничивающим. При увеличении е2 от 0 до 4 максимум относительного момента первого ротора снижается с 1 до 0,1 (в десять раз). Одновременно происходит смещение критического числа Рейнольдса ек , при котором тх достигает максимума, в сторону больших значений (с 1 при е2 = 0 до 4,1 при е2 = 4 ). Влияние реакции вихревых токов, наводимых в первом роторе на электромагнитные процессы во втором роторе также оказывается размагничивающим.

Для относительного суммарного электродинамического момента с учетом (12) получают следующее выражение:

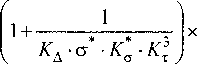
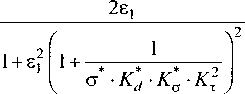
дт

Приравняв нулю частную производную --, можно определить максимальный электродинамический момент и его положение на механической характеристике, характеризуемое критическим

Таким образом, увеличение о* приводит к увеличению максимального момента при одновременном уменьшении е_1Л- , что подтверждается зависимостями т_х= f^£_x^, т_г = /(si), для о* = 2, о* = 0,5 рассчитанными по формулам (11) и (13) и представленными на рис. 2. Физически возрастание максимума относительного момента объясняется тем, что при увеличении о₂ при постоянном Ст] уменьшается размагничивающее влияние внутреннего ротора (II) на внешний ротор (I) и наоборот при увеличении ст, при постоянном о₂ размагничивающее влияние внешнего ротора на внутренний ротор становится интенсивней.

Анализ выражений (И) и (13) показал, что при малых значениях о* момент создается в ос новном внутренним ротором; при а = —L = оо момент создается внешним ротором и е^ = 1;

А2 „                 , аналогично, при —— = 0 т = тх гхк = 1, а при

А]

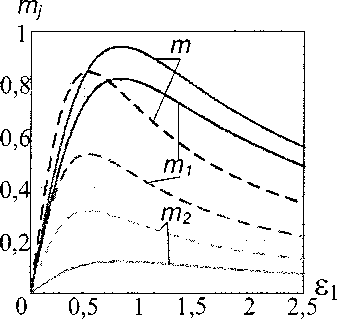
Рис. 2. Зависимости относительных моментов от Е[

при О' = 0,5 (пунктирная линия) и о =2 (сплошная

Как видно из этого выражения, критическое значение е]л- зависит от соотношения электриче

линия) для K_dx = 1, К_х

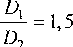
Если принять, что D_x jD₂ = 1 задача сводится к решению задачи для ЭДЭ с одним ротором и также как в рассмотренных выше случаях хорошо согласуются с результатами, полученными для ЭДЭ с полым немагнитным ротором [7].

Таким образом, на основании полученных результатов, можно сделать вывод о том, что для исключения взаимного размагничивающего влияния роторов, необходимо обеспечить конструктивно раздельные, не влияющие друг на друга, пути магнитных потоков, пронизывающих роторы с различной проводимостью, или поэтапное включение в работу этих роторов при одном и том же магнитном потоке.

В этом случае электромагнитный момент, создаваемый каждым ротором, определяется по формулам:

• -    момент, создаваемый первым ротором: ^М1=Р_Д⁶°_Г 2Ш,Ла-^--^ = М_?)Г^ (16)

⁴Но^л            1 + ЕГ       1 + е{

• -    момент, создаваемый вторым ротором: ^М2=р Л ^KD2-^2a'^2-7^ = ^M&27^- О⁷)

^Uo^d2             1 + £2       1 + £2

Суммарный момент:

М = М₆ (/И; + ти₂) ⁼

= р ---—лД ^а-А, ■

4^1     *

2гх

1+е?

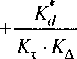
2е2

1 + £2

• (18)

С учетом (14) относительный суммарный момент:

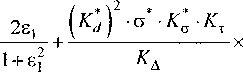
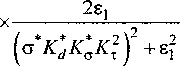
На рис. 3 показаны графики зависимости суммарного момента от относительной скорости вращения при различных ст*. Видно, что суммарный момент в этом случае получается больше, чем при взаимном влиянии вторичных полей. При равенстве электрических проводимостей роторов ст* = 1, электромагнитный момент ЭДЭ с двойным ротором в полтора раза превышает электромагнитный момент, создаваемый однороторным ЭДЭ. При этом максимум кривой смещен в сторону больших частот (скоростей).

Произведенные расчеты показывают, что увеличение ст* приводит к уменьшению максимума суммарного момента и к одновременному увеличению критической скорости, при которой достигается максимум. Это связано с тем, что уменьшение электрической проводимости второго ротора при неизменной электрической проводимости первого ротора приводит к уменьшению плотности вихревых токов во втором роторе, а, следовательно, и к уменьшению создаваемого им электромагнитного момента.

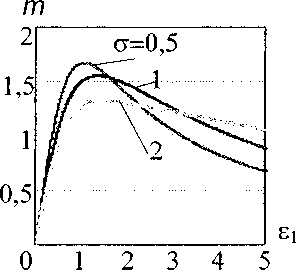
Рис. 3. Влияние ст на суммарный момент

Выводы

• 1.    Получены выражения для определения электромагнитного момента двухроторного ЭДЭ для случая взаимного влияния вторичных полей и без него, позволяющие давать рекомендации по проектированию таких элементов.

• 2.    Показано, что применение конструктивной схемы с двумя роторами, исключающей их взаимное размагничивающее влияние, целесообразно. Это приводит к существенному увеличению суммарного тормозного момента, создаваемого ДЭДЭ.

• 3.    Максимум суммарного электромагнитного момента ДЭДЭ больше максимального момента демпфера с одним ротором примерно на 50 %. Максимальный момент сдвигается в сторону больших частот.