Механические и конечно-элементные модели кератопротезов роговицы глаза
Автор: Соловьев А. Н., Глушко Н. И., Епихин А. Н., Свейн М., Лесняк О. Н., Иванов А. Е.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 4 т.20, 2020 года.
Бесплатный доступ
Введение. При разработке глазных протезов возникает ряд проблем, одна из которых - конструирование соединения между жесткой оптической частью и мягкой тканью роговицы. Их модули Юнга могут отличаться на три порядка. При этом возникает задача создания промежуточного слоя, возможно с градиентными свойствами, назначение которого - исключить травмирование мягких биологических тканей. Рассматривается два типа кератопротеза: с опорной пластиной и с промежуточным функционально-градиентным слоем. Для первого типа рассчитано напряженно-деформированное состояние. Для второго проведено аналитическое и конечноэлементное моделирование взаимодействия цилиндрического оптического протеза, промежуточного неоднородного слоя и роговицы в упругой среде. Рассмотрены два варианта: без учета кривизны (круглая плита или пластина) и с учетом кривизны (сферический купол или оболочка). Цель работы - исследование напряженно-деформированного состояния керапротеза и роговицы в области контакта.Материалы и методы. Математические модели рассматриваемых конструкций - это краевые задачи линейной теории упругости. Аналитическое решение построено для упрощенной модели в виде составной круговой пластины. Пространственные трехмерные задачи и задачи в осесимметричной постановке решаются методом конечных элементов. Конечноэлементное моделирование рассматриваемых конструкций проводилось в CAE-пакете ANSYS и ACELAN.Результаты исследования. Построены CAD-модели кератопротезов с условиями закрепления и нагружения. Установлена нагрузка на керапротез под действием внутреннего глазного давления. Рассчитано напряженно-деформированное состояние элементов кератопротеза и роговицы. Особое внимание уделено окрестности ее контакта с кератопротезом.Обсуждение и заключения. Результаты расчета осевых смещений и механических напряжений в кератопротезе первого типа показывают, что выбранные для него геометрические параметры удовлетворяют кинематическим и прочностным требованиям. Предложенные в работе модели деформированного состояния мягких биологических тканей позволяют оценить их травмирование при использовании кератопротеза второго типа, а также выбрать геометрические параметры и градиентные свойства промежуточного слоя.
Глазной протез, неоднородные упругие свойства, пластина, оболочка, метод конечных элементов
Короткий адрес: https://sciup.org/142225511
IDR: 142225511 | УДК: 539.3 | DOI: 10.23947/2687-1653-2020-20-4-350-359
Текст научной статьи Механические и конечно-элементные модели кератопротезов роговицы глаза
УДК 539.3

Mechanical and finite element models of corneal keratoprostheses
-
A. N. Soloviev1, N. I. Glushko1, A. N. Epikhin2, M. Swain3, О. N. Lesnyak1, А. Е. Ivanov1
-
1 Don State Technical University (Rostov-on-Don, Russian Federation)
-
2 Rostov State Medical University (Rostov-on-Don, Russian Federation)
-
3 Sydney University (Sydney, Australia)
Introduction. When developing ocular prostheses, a number of problems arise, one of which is the construction of the connection between the hard optical part and the soft corneal tissue. Their Young's modules can differ by three orders of magnitude. In this case, the problem arises of creating an intermediate layer, possibly with gradient properties, whose purpose is to exclude injury to soft biological tissues. Two types of keratoprostheses are considered: the first type with a support plate and the second type with an intermediate functionally gradient layer. The stress-strain state of the prosthesis is calculated for the first type. For the second type, analytical and finite element modeling of the interaction of a cylindrical optical prosthesis, an intermediate inhomogeneous layer, and the cornea was carried out in the elastic media. Two versions are considered: discounting the curvature (circular plate or plate) and with account of the curvature (spherical dome or shell). The work objective is to study the stress-strain state of the keraprosthesis and cornea in the contact area.
Materials and Methods. Mathematical models of the structures under consideration are the boundary value problems of the linear elasticity theory. The analytical solution is constructed for a simplified model in the form of a composite circular plate. Spatial three-dimensional problems and axisymmetric problems are solved by the finite element method. Finite element modeling of the considered structures was performed in the CAE package ANSYS and ACELAN.
Results. CAD models of keratoprostheses with conditions of fixing and loading are constructed. The load acting on the keraprosthesis under the effect of intraocular pressure was determined. The stress-strain state of the keratoprosthesis and cornea elements was calculated. Special attention was paid to the area of its contact with the keratoprosthesis.
Discussion and Conclusions. The results of calculating the axial displacements and mechanical stresses in the first type of keratoprosthesis show that the selected geometric parameters meet the kinematic and strength requirements. The proposed models of the deformed state of soft biological tissues provide assessing their injury when using a keratoprosthe-sis of the second type, as well as selecting the geometric parameters and gradient properties of the intermediate layer.
Funding information: the research is supported by the Government of the Russian Federation (grant no. 14.Z50.31.0046).
Введение. Кератопротез — это бесклеточный искусственный имплантат, сконструированный таким образом, что цилиндрическая оправа удерживает оптику. Кератопротез заменяет удаленную часть роговицы. Раньше трансплантации роговицы имели высокие показатели инфицирования и отторжения. В конце 1980-х годов наибольшее распространение получила конструкция «ядро и юбка» (биоинтегрируемая «юбка» окружает оптику). Важны были не только размеры, но и расположение пор в пористой юбке. Такие кератопротезы, как AlphaCor (раннее название Chirila) представляли собой полиметилметакрилатное устройство с центральной оптической областью, слитой с окружающей губчатой юбкой.
Современные кератопротезы состоят из оптического элемента и опорной пластины. Оптический прозрачный элемент имеет форму цилиндра или линзы. Опорная пластина, соединенная с оптическим элементом, может иметь различные формы: колечка с отверстиями, колесика со спицами, ушек или амебовидных ножек. В книге С. Н. Федорова [1] приведены описания различных видов и форм кератопротезов и креплений. Основное осложнение после кератопротезирования — асептический некроз роговицы, развивающийся спереди от опорного крепления имплантата. Именно это осложнение довольно часто приводит к отторжению кератопротеза [1]. Основная причина асептического некроза — блокирование поступления жизненно необходимых веществ в слои роговицы, которые располагаются над опорой кератопротеза. В связи с этим для изготовления опорной пластины необходимо использовать биосовместимый материал, который позволит тканям роговицы прорасти сквозь опорное крепление.
Механика
Американские исследователи описали микропористую опорную пластину1 для кератопротеза из растянутого политетрафторэтилена (ПТФЭ). Его структура имеет конфигурацию в виде узлов полимера, которые соединяются фибриллами длиной 7–8 мкм. Слишком маленькие поры препятствуют прорастанию тканей роговицы. Поэтому необходимо дополнительно пронизывать протез порами, перпендикулярными поверхностям опорной пластины диаметром 20–150 мкм (лучше 50 мкм). Толщина опорной пластины должна составлять около 0,2 мкм, но не более 0,3 мкм.
В модели с опорным креплением в форме кольца1 оптический элемент сделан из прозрачного вещества типа полиметилметакрилата (ПММА), крепление — из гидрофильного пористого материала с волокнистой структурой, через который могут прорастать ткани роговицы. Из этого волокна сформирована опорная пластина толщиной 0,15–0,30 мкм. Кольцо с внешним диаметром около 9,5 мм надето на оптический элемент. Его передняя часть — цилиндрическая, задняя имеет форму усеченного конуса, большее сечение которого направлено внутрь. Опорная пластина имеет упругие характеристики, необходимые для предотвращения отторжения кератопротеза и некроза из-за давления окружающих тканей глаза.
В другой конструкции2 опорная пластина представляет собой две параллельные оболочки, отстоящие друг от друга на 0,4–0,7 мкм. Оптимальное расстояние 0,3±0,02 мм. Оболочки конической формы прикреплены к цилиндрическому оптическому элементу. Материал опорных пластин должен быть биозаселяемым, следовательно, предполагается, что его пористость — 50% и выше, поры должны быть открыты, их диаметр — около 20–100 мкм.
Элементы кератопротеза3, предложенного российскими учеными (рис. 1):
— опорная пластина — 1 (радиус кривизны 7–10 мм, внешний диаметр 7–12 мм);
-
— оптическая часть — 2 (оптический элемент в форме цилиндра с закругленными торцами, которые служат для выбора диоптрий);
-
— цилиндрическая поверхность оптического элемента с винтовой нарезкой — 3;
— соединительная шайба — 4 (жестко скреплена с опорной пластиной).
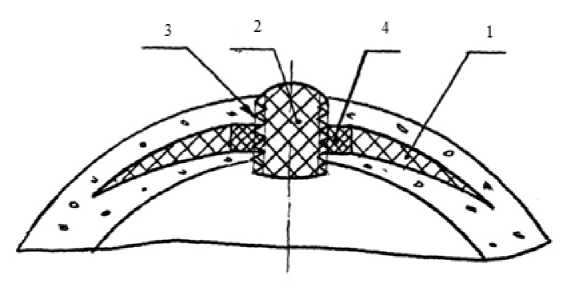
Рис. 1. Схема кератопротеза
Кератопротез имплантируется в интраламеллярный карман роговицы. Опорная пластина располагается внутри роговицы глаза, а оптический элемент пронизывает всю роговицу.
Имплантат для укрепления роговицы4 представляет собой пластину — круглую, овальную, в форме трилистника, ромашки или выпукло-вогнутой линзы с радиусом кривизны 7–10 мм. В центре линзы может быть цилиндрическое отверстие. В структуре материала имплантата объемная доля пустот — 15–40 %, их удельная поверхность — 0,25–0,55 мкм2/мкм3, среднее расстояние между пустотами — 25–50 мкм, средняя объемная хорда — 8–25 мкм. Имплантат представляет собой выпукло-вогнутую линзу, радиус кривизны которой соответствует радиусу кривизны роговицы пациента. В центральной части толщина имплантата — 0,3– 0,7 мм, на краях — 0,01 мм.
В другой модификации кератопротеза5, в отличие от описанного выше, опорный блок выполнен из пористого никелида титана, кривизна пластины совпадает с кривизной роговицы. Опорная пластина устанавливается на поверхности роговицы и ретенционно фиксируется аллотрансплантатом склеры. Цилиндрический оптический элемент соединяется с опорной пластиной методом тугой посадки. Такой подход позволяет более эффективно лечить бельма, благодаря быстрой и успешной интеграции пористого имплантата (базиса) с окружа- ющими тканями и механически прочной фиксации оптического элемента, которая снижает опасность репозиции кератопротеза.
Разработчик комбинированного кератопротеза1 отмечает, что опорная часть имплантата должна максимально сопротивляться выталкивающему воздействию давления внутриглазной жидкости на оптическую часть кератопротеза и при этом минимально деформировать надлежащие ткани. Материал опорной части должен быть не только биосовместим, но и структурирован таким образом, чтобы обеспечить сращение над- и подлежащих слоев роговицы, разделяющихся в процессе имплантации кератопротеза. Ранее упоминались кера-топротезы с оптическим элементом из прозрачного вещества (например, из ПММА) и опорной пластиной в форме кольца из гидрофильного пористого материала ПТФЭ или полиэтилена2. Их использование обеспечивает сращения над- и подопорных слоев роговицы за счет высокой пористости материала (от 50 %) и диаметра пор до 100 мкм. Главные недостатки таких конструкций — избыточная гибкость и низкая механическая прочность. Эти характеристики не позволяют продолжительное время надежно удерживать и фиксировать установленный кератопротез с большой оптикой.
Оптическая часть комбинированного кератопротеза выполнена из прозрачного упругого полимера, насыщенного УФ-адсорбентом. По форме это съемный болт диаметром 5-6 мм. Передний торец — грибовидный, другие — сферические (асферические). Гаптическая часть — это опорный диск наружным диаметром 812 мм и толщиной 0,3-0,9 мм. На ее боковую поверхность нанесена резьба. Для этой части используют пористый (перфорированный) твердый (упругий) ареактивный полимер (металл) с объемной долей пустот не более 50 %. Переднюю часть гаптического элемента делают из биологических материалов, заднюю — из искусственных биосовместимых. Опорный диск задней части — плоский и перпендикулярно соединяется с размещенным в центре опорным полым цилиндром. Соединение обеспечивает канавка и (или) фланец на внешней задней части цилиндра. Профиль и диаметр внутренней резьбы цилиндра соответствуют резьбе оптического болта. Опорный диск может переходить во втулку, которая обхватывает опорный цилиндр снаружи. Опорная пластина спереди соединена с круглым биодиском, который вырезается из свежеизъятых или консервированных стерильных биологических материалов, которые представляют собой разновариантные послойные сочетания биологических тканей. Перед соединением части кератопротеза стерилизуют. Соединение проводят в стерильных условиях. Сборку выполняют непосредственно перед протезированием или заранее (в этом случае имплантат хранится до операции). Внешний диаметр биодиска должен быть больше внешнего диаметра опорного диска на 0,3-1 мм, в центре биодиска делается соосное отверстие с диаметром, соответствующим наружному диаметру покровной втулки или опорного цилиндра.
Для сквозной кератопластики разработаны модели с использованием различных материалов, конструкций и хирургических методов [2]. Однако проблема окончательно не решена. Это подтверждают случаи слепоты роговицы у пациентов с повторной недостаточностью трансплантата или с тяжелым поражением глазной поверхности [3-6]. Вопросы кератопротезирования при заболеваниях роговицы и глазной поверхности рассмотрены в [7]. Обзор по применению бостонского кератопротеза представлен в [8]. В [9] обсуждаются осложнения с широкими последствиями при применении кератопротезов
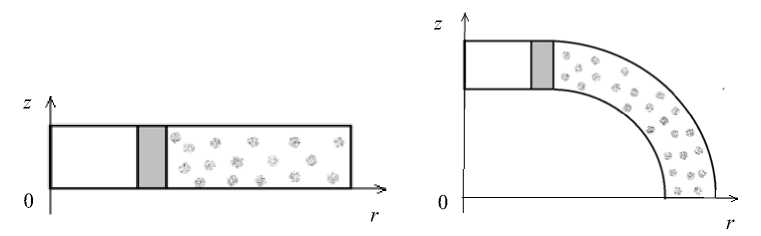
В настоящей работе рассматриваются два типа кератопротезов с оптическим элементом цилиндрической формы. Схема первого типа представлена на рис. 1. Во втором типе на цилиндрической поверхности присутствует некоторый промежуточный слой с неоднородными механическими свойствами. На рис. 2 представлена схема половины осевого сечения кератопротеза второго типа без учета кривизны ( а ) и с учетом кривизны роговицы ( б). Серым выделен слой с функционально градиентными свойствами. Он нужен для нетравматического контакта оптики с мягкими тканями роговицы.
а ) б )
Рис. 2. Половина осевого сечения кератопротеза: модель пластины ( а ), модель купола ( б )
Механика
Методом конечных элементов построены аналитические и численные модели имплантации кератопро-теза в роговицу. Исследовано напряженно-деформированное состояние роговицы в области контакта. Этим определяются цели настоящей работы. Для керапротеза первого типа: исследование его напряженно-деформированного состояния под действием внутреннего глазного давления в предположении, что внешний край опорной пластины закреплен. Для керапротеза второго типа: исследование напряженно-деформированного состояния роговицы в окрестности контакта с кератопротезом, внешний слой которого представляет собой конструкцию, позволяющую уменьшить травмирование мягких тканей. Этот промежуточный (интерфейсный) слой моделируется как полый цилиндр с функционально градиентными механическими свойствами.
В работе рассматриваются три модели.
-
I. Аналитическая — для имплантированного протеза на основе изгиба составной круговой пластины.
-
II. Конечноэлементная — для имплантированного протеза на основе составной круговой плиты.
-
III. Конечноэлементная модель — для имплантированного протеза на основе составного сферического купола.
Решаются задачи моделирования для:
-
— кератопротеза первого типа (А),
-
— кератопротеза второго типа (Б).
Материалы и методы. Континуальная постановка задач. Общая математическая постановка исследуемой проблемы (для задач А и Б) представляет собой статическую краевую задачу теории упругости для составного изотропного тела. Для неизвестных й = ( их, u 2 , и 3) — компоненты вектора перемещений система дифференциальных уравнений имеет вид [10]:
Gi,j= 0, 6kl = 2 (uk,l + ulk) , где oj , cijkl, ekl — компоненты тензоров напряжений, упругих постоянных и деформаций соответственно.
Граничные условия ставятся для векторов смещений и напряжений на соответствующих поверхностях S u и S t :
ui Isu = ui0(x, t), x e Su, ti St = j |st = q(x, t), x e St,(3)
где n j — координаты единичного вектора внешней нормали.
Кроме того, для задачи Б (рис. 2) подтела имеют различные свойства, а именно:
-
— два из них (цилиндрический оптический протез и роговица) — однородные, с модулями упругости Er 1 и Er3 ;
— функционально-градиентный модуль упругости интерфейсного слоя — Er2 = Er2 ( r ).
Правая сторона закреплена, на левой задаются условия симметрии. На нижнюю границу действует равномерно распределенное давление, которое соответствует избыточному внутриглазному давлению по сравнению с атмосферным. На интерфейсных границах задаются условия непрерывности.
Для исследования модели (I) краевая задача (1)-(3) сводится к системе обыкновенных дифференциальных уравнений (4), (5) и (6) для первого, второго и третьего участка соответственно относительно угла поворота нормали 0 (r) при степенной зависимости от радиуса модуля упругости второго участка [11]:
(^9(7-)^ г2 + (^ 9(r)) r - 9(r) = 2 Klqr3, (£ 9(г) ) г2 + Ч^9(гУ + ^29(r) +(^9(r))r - 9(r) = (£9(r))r2 + Q^^r-9^) = 2 K3q(r2 -^r, где K = 1/ D , D — цилиндрическая жесткость.
Результаты исследования
Аналитическое решение
Общее решение системы (4)-(6) представлено ниже.
Первый участок:
:-а
,
Третий участок:
9(г) = rC2 + -^Klqr3
+ —.
Г
Второй участок:
9(r) = у + rC2 -^KSq^lnMr2 -r2)r.
1 .1 / . . „ ■. 1 .1 / . . „ ■.
9(г) = Т -2а+2^а -4OS2+4 C 2 + т -2а+2^а - 4OS2+4 C1 +
1 ^.--(«r^-rM-r2 + 3г,2)„- 8,-2)
2 (8 + (в2 - 3)а)а(В2 - 1)
при
'"^
Ег 2 - Ег . ( г ) ; D 2 - 12(1-9 1 ) , а - т(^)
Произвольные постоянные Ci общего решения (7) определяются из граничных условий на правом конце и условий стыковки, причем для первого участка C 1 = 0 .
Конечноэлементное решение
Численное моделирование проведено в конечноэлементных пакетах ANSYS и ACELAN [12, 13].
Численные результаты для кератопротеза первого типа. На рис. 3 представлена CAD-модель кера- топротеза с условиями закрепления и нагружения.
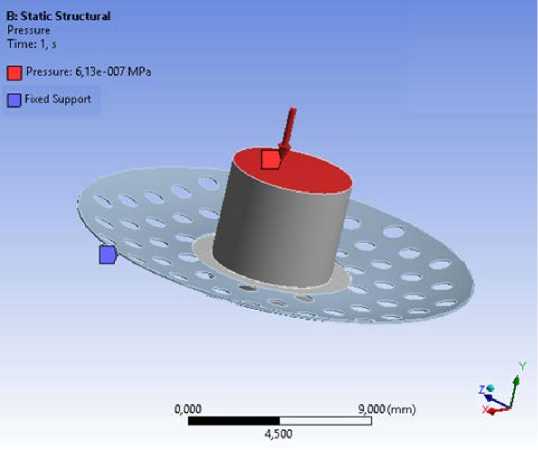
Рис. 3. Геометрическая модель с условиями закрепления и нагружения
Внешний край опорной пластины закреплен, на оптический элемент действует распределенное давление. Нормальное внутриглазное давление составляет от 12 до 21 мм ртутного столба. Давление в 45 мм/рт. ст. является критичным. В этом случае операция еще может спасти глаз. При более высоком давлении глаз спасти практически невозможно. На данный кератопротез действует нагрузка в 46 мм/рт. ст.
На рис. 4 представлено распределение осевого смещения ( а ) и напряжения по Мизесу ( б) на конечноэлементной сетке модели.
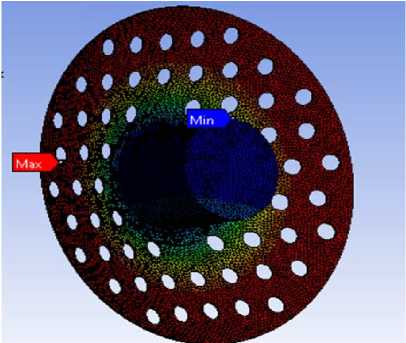
a )
Рис. 4. Распределение на конечноэлементной модели характеристик напряженно-деформированного состояния: осевого смещения ( а ) и напряжений по Мизесу ( б )
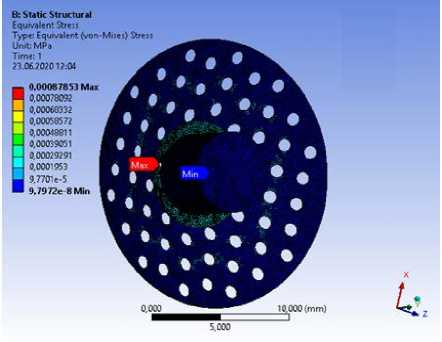
б )
Механика
Максимальные напряжения возникают в месте соединения оптического элемента с опорной пластиной, но их значения не превосходят предела прочности выбранного материала.
Далее рассматриваются результаты расчетов для задачи Б в осесимметричной постановке. Так, на рис. 5–7 представлены компоненты напряженно-деформированного состояния (II).

a ) б )
Рис. 5. Расчет перемещений: конечноэлементная сетка на деформированной конструкции ( a ), распределение вектора смещений ( б )
σ r
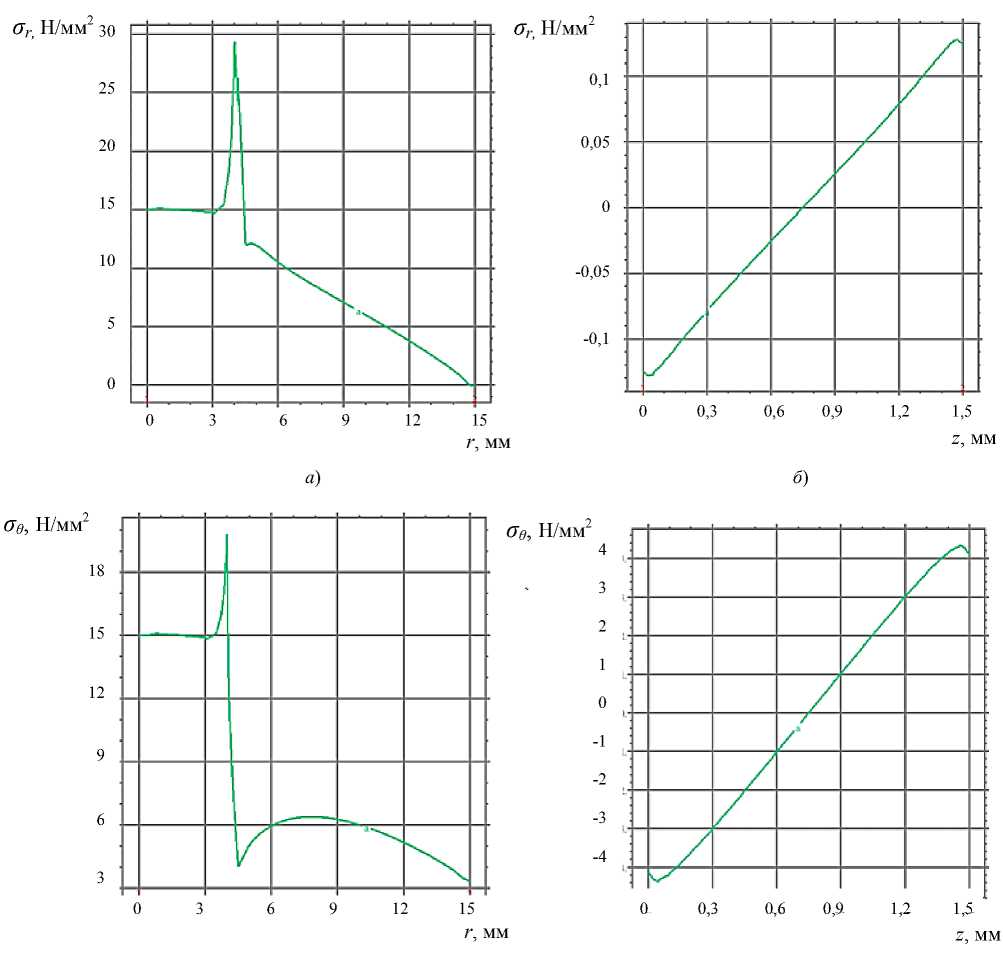
в )
г )
Рис. 6. Расчет компонентов тензора напряжений. Зависимость от радиуса: радиальных напряжений на верхней границе ( a ), на интерфейсной границе с роговицей ( б ), угловых напряжений на верхней границе ( в ), на интерфейсной границе с роговицей ( г )
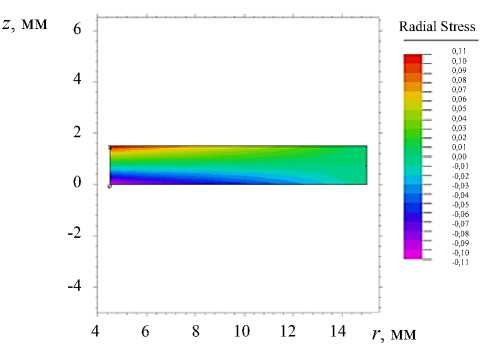
a )
Рис. 7. Распределение компонент напряжений внутри области: радиальных напряжений ( a ), угловых напряжений ( б )
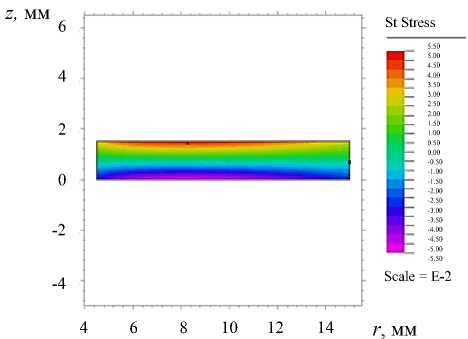
б )
Характеристики напряженно-деформированного состояния модели III представлены на рис. 8–11.
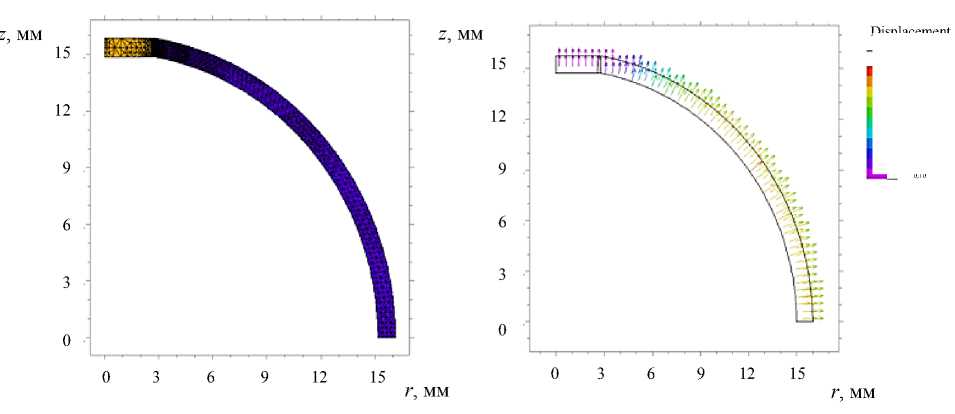
a )
б )
Рис. 8. Расчет перемещений купола: конечноэлементная сетка на деформированной конструкции ( a ),
распределение вектора смещений ( б )
z , мм 15
Shear Stress
Scale
0 3 6 9 12 15
r
, мм
a )
8,50 8,00 7,50 7,00
6,50 6,00
5,50 5,00 4,50 4,00
3,50 3,00 2,50 2,00
1,50 1,00 0,50 0,00 -0,50 -1,00
= E-2
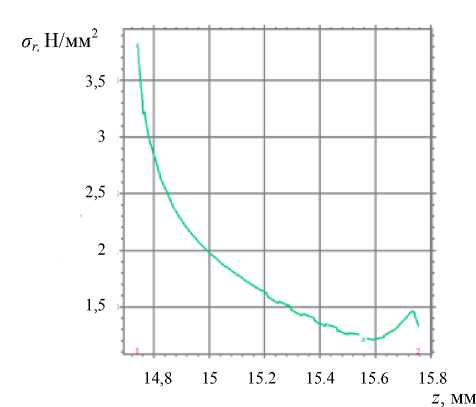
б )
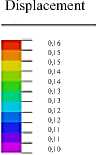
Рис. 9. Расчет радиальных напряжений: распределение в области ( a ), на интерфейсной границе с роговицей ( б )
Механика
z , мм
St Stress
Scale
0 3 6 9 12 15
r ,
мм
4,00 3,80 3,60 3,40 3,20 3,00 2,80 2,60 2,40 2,20 2,00
1,80 1,60 1,40 1,20 1,00 0,80 0,60 0,40 0,20 0,00
= E-2
σθ , Н/мм 12
14,8 15 15
,2 15
,4 15
,4 15, z,
8 мм
a )
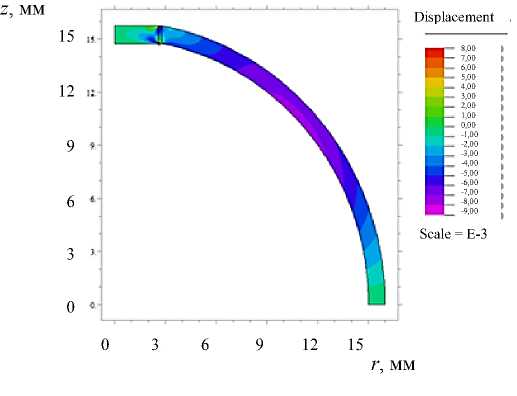
a )
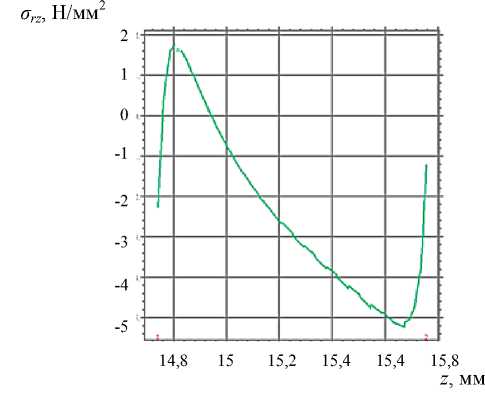
Рис. 11. Расчет касательных напряжений: распределение в области ( a ), на интерфейсной границе с роговицей ( б )
Рис. 10. Расчет угловых напряжений: распределение в области ( a ), на интерфейсной границе с роговицей ( б )
б )
Обсуждение и заключения. Рассмотрены два типа кератопротезов и построены их механические и математические модели. Для первого типа кератопротеза с опорной пластиной исследовано его напряженно-деформированное состояние, создана конечноэлементная модель в ANSYS. Показано, что при максимальном глазном давлении возникающие максимальные напряжения не превосходят пределов прочности выбранных материалов. Для второго типа кератопротеза построено аналитическое решение без учета кривизны и конечноэлементное решение в пакете ACELAN с учетом кривизны роговицы. Рассчитаны характеристики напряженно-деформированного состояния, в том числе на интерфейсной границе с роговицей. Это позволяет оценить ее травмирование и выбрать геометрические параметры и градиентные свойства промежуточного слоя.
Список литературы Механические и конечно-элементные модели кератопротезов роговицы глаза
- Федоров, С. Н. Кератопротезирование / С. Н. Федоров, З. И. Мороз, В. К. Зуев. - Москва: Медицина, 1982. - 144 с.
- Keeler, R. Guillaume Pellier de Quengsy: a bold eye surgeon / R. Keeler, A. D. Singh, H. S. Dua // British Journal of Ophthalmology. - 2014. - Vol. 98 (5).-P. 576-578. DOI: 10.1136/bjophthalmol-2014-305269
- External Disease Panel. Preferred Practice Pattern® Guidelines. Corneal Ectasia / American Academy of Ophthalmology Cornea. - San Francisco: American Academy of Ophthalmology, 2019. - Vol. 126 (1). - P. 171215.
- Belin, M. W. Suggested guidelines for reporting keratoprosthesis results / M. W. Belin, J. L. Guell, G. Grabner // National Center for Biotechnology Information. - 2016. - 35 (2). - Р. 143-144.
- Charoenrook, V. Comparison of long-term results between osteo-odonto-keratoprosthesis and tibial bone keratoprosthesis / V. Charoenrook, R. Michael, M. F. de la Paz// The Ocular Surface. - 2018. - No. 16. - Р. 259-264.
- Khandekar, R. Impact of Cataract Surgery in Reducing Visual Impairment: A Review / R. Khandekar, A. Sudhan, B. K. Jain// Middle East African Journal of Ophthalmology. - 2015. - Vol. 22 (1). - P. 80-85.
- DOI: 10.4103/0974-9233.148354
- Sanchez Ferreiro, A. V. Keratoprosthesis in cornea and ocular surface diseases / A. V. Sanchez Ferreiro, L. Munoz Bellido // Archivos de la Sociedad Espanola de Oftalmologa (English Edition). - 2013. - Vol. 88 (8). - P. 327-328.
- Cortina, M. S. Staged ocular fornix reconstruction for glaucoma drainage device under neoconjunctiva at the time of Boston type 1 Keratoprosthesis implantation / M. S. Cortina, F. I. Karas, Ch. Bouchard// The Ocular Surface. - 2019. - Vol. 17 (2). -P. 336-340.
- Park, J. Retroprosthetic membrane: A complication of keratoprosthesis with broad consequences / J. Park, P. Phrueksaudomchai, M. Soledad Cortina // The Ocular Surface. - 2020. - Vol. 18 (4). - P. 893-900.
- Новацкий, В. Теория упругости / В. Новацкий. - Москва: Мир, 1975. - 872 с.
- Бояршинов, С. В. Основы строительной механики / С. В. Бояршинов. - Москва: Машиностроение, 1973. -456с.
- Belokon, A. V. Partitioned schemes of the finite-element method for dynamic problems of acoustoelectroelasticity / A. V. Belokon, V. A. Eremeyev, A. V. Nasedkin// Journal of Applied Mathematics and Mechanics. - 2000. - Vol. 64 (3). -P. 367-377.
- Belokon, A. V. New schemes for the finite-element dynamic analysis of piezoelectric devices / A. V. Belokon, A. V. Nasedkin, A. N. Solov'yev // Journal of Applied Mathematics and Mechanics. - 2002. - Vol. 66 (3). -P. 481-490.


