Механизм формирования обратного потока энергии в остром фокусе

Оптические вихревые пучки известны давно [1]. Такие пучки имеют спиральную фазу, что влияет на свойства распространения этих пучков [2]. Интерес к ним обуславливается их широким применением. Вихревые лазерные пучки используются в телескопах для обнаружения далёких планет [3], для захвата и управления движением микрочастиц в оптическом пинцете [4, 5], вращения частиц оптическим гаечным ключом [6], передачи микрочастице углового момента [7], увеличения объёма передачи информации в системах оптической связи [8], в квантовой информатике [9, 10] и высокоразрешающей электронной микроскопии [11]. Еще одна возможность использования оптических вихрей – создание пучков с областью, где направление течения энергии обратно к направлению распространения пучка [12–14]. Мы недавно показали, что в остром фокусе оптического вихря с целым топологическим зарядом, большим 1, и с круговой поляризацией имеет место обратный поток энергии [12]. В [13] теоретически и численно показано, что в остром фокусе вихревого светового поля с круговой поляризацией и топологическим зарядом 2 обратный поток возникает на оптической оси и по величине сравним с прямым потоком энергии. В [14] численно показано наличие обратного потока на оптической оси в фокусе поляризационного вихря второго порядка. В [15] показано, что обратный поток можно сформировать с помощью металинзы.

Эффект обратного потока энергии изучался ранее в работах и других авторов. В [16] получено простое выражение для продольной компоненты вектора Пойн-тинга в фокусе апланатической системы при фокусировке плоской волны с линейной поляризацией, из ко- торого следует, что на некоторых радиусах (вблизи тёмных колец) имеет место обратный поток энергии. Обратный поток также был обнаружен при сложении четырёх плоских волн в [17]. Но автор посчитал, что такое поведение вектора Пойнтинга не имеет физического смысла. В [18] численно показано, что при фокусировке параксиального Гауссова пучка с помощью сферической линзы, ограниченной апертурой, в плоскости фокуса и рядом с ней на некоторых радиусах возникают темные кольца Эйри, в которых имеет место фазовая сингулярность. Позже Берри с помощью асимптотик показал, что такие сингулярности возникают в фокусе непараксиального Гауссова пучка и без ограничения линзы апертурой [19]. В [19] также показано, что вокруг сингулярности фазы возникает круговой поток энергии, в том числе и обратный поток. В [20] Воляр численно показал, что в фокусе линейно поляризованных векторных непараксиальных пучков Гаусса (сферические моды низших порядков) сечение пучка эллиптическое и вокруг центрального пятна имеются «острова сингулярности» (вместо колец Эйри), рядом с которыми возникает обратный поток энергии. В [21] аналогичные «острова сингулярности» и обратный поток рядом с ними численно обнаружены в плоскости фокуса векторных непараксиальных Гауссовых вихревых пучков с круговой поляризацией. В [22] на простом примере соосной интерференции двух Гауссовых пучков показано, что вокруг кольца, на котором интенсивность равна нулю, формируется тороидальный поток энергии, в том числе и обратный поток. В работах [16–22] обратный поток возникает в стороне от оптической оси, в малых периферийных областях, и мал по величине. В [23] показано, что при соосном сложении двух векторных пучков Бесселя с ТЕ- и ТМ- поляризациями обратный поток может быть и на оптической оси. В [24, 25] обсуждается концепция оптического трактора, когда сила, действующая на частицу, направлена в обратную сторону по отношению к освещающему пучку света. Показывается, что не всегда наличие обратного потока приводит к отрицательной силе, действующей на частицу. И наоборот, сила, толкающая (или тянущая) частицу назад, может возникать и без обратного потока. В [26] численно показано наличие обратного распространения энергии в векторном пучке Бесселя с дробным топологическим зарядом. Такой световой пучок фактически является линейной комбинацией счётного числа обычных мод Бесселя. В [27] теоретически получены выражения для плотности вектора Пойнтинга Х-пучков и получены необходимые условия для появления обратного потока энергии. В [28] численно показано наличие обратного течения энергии в непараксиальном ускоряющемся 2D-пучке Эйри. А в [29] показано, что обратный поток имеет место для непараксиальных векторных параболических пучков Вебера. В [30] теоретически рассматриваются условия, которые нужно наложить на световое поле, чтобы оно локально проявляло обратное распространение (или имел место обратный поток энергии). Из приведённого обзора видно, что наиболее широко для получения областей с обратным потоком энергии используются вихревые лазерные пучки, причём для получения обратного потока необходимо использовать круговую поляризацию падающего поля.

Возможно, в световых полях, в которых фазовые и поляризационные сингулярности образуют в пространстве многосвязные узлы ( vortex knot ) [31 – 33], также имеет место обратное распространение света (обратный поток световой энергии).

В данной работе мы попытаемся объяснить механизм возникновения обратного распространения света, предсказанного в [12 – 15]. На простом примере интерференции четырёх плоских волн [17] со специально подобранными линейными поляризациями мы покажем детально, как формируется обратный поток энергии. Получим формулы для величины обратного потока в зависимости от угла схождения плоских волн. Найдём координаты и величины всех областей, в которых имеет место обратное распространение света. Мы также покажем, что рассмотренная модель четырёх плоских волн также хорошо объясняет наличие обратного потока энергии на оптической оси в остром фокусе поляризационного вихря второго порядка, который был рассмотрен в [14]. В заключении будет показано, что рэлеевская наночастица, помещённая на оптической оси в области обратного потока, будет двигаться в обратном направлении. То есть в случае острой фокусировки света [14] величины обратного потока энергии на оптической оси достаточно для того, чтобы рассеивающая сила толкала частицу назад.

Интерференция четырёх плоских волн с линейной поляризацией

Рассмотрим картину интерференции четырёх когерентных и монохроматических плоских волн со специально подобранными линейными поляризациями (рис. 1). Вектора напряжённости электрического поля En, n = 1, 2, 3, 4 этих четырёх плоских волн пусть имеют вид

E 1 = ( e x cos a + e z sin a ) exp ( - ikx sin a + ikz cos a ) ,

E 2 = - e _x exp ( - iky sin a + ikz cos a ) ,

E 3 = ( e _x cos a - e _z sin a ) exp ( ikx sin a + ikz cos a ) ,

E 4 = - e _x exp ( iky sin a + ikz cos a ) ,

где (x, y, z) – декартовы координаты, (ex, ey, ez) – правая тройка единичных векторов, направленных вдоль координатных осей, k - волновое число света, a - угол наклона плоских волн к оптической оси z. Из уравнения Максвелла для монохроматического поля rot E = ikH

можно найти выражения для векторов напряжённости магнитного поля H n , n = 1,2,3,4 этих четырёх плоских волн:

H1 = ey exp (-ikx sin a + ikz cos a), H2 =-(ey cosa + ez sina)x x exp (-iky sin a + ikz cos a), H3 = ey exp (ikx sin a + ikzcos a), H4 =-( ey cos a- e z sin a)x x exp (iky sin a + ikz cos a).

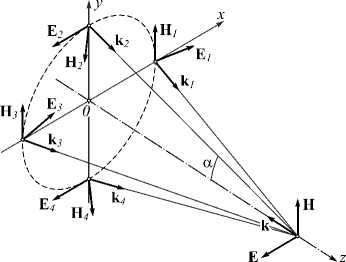
Рис. 1. Схема сложения четырёх плоских волн с линейными поляризациями

Из выражений (1) и (3) получим выражение для распределения интенсивности электрического поля

Ia = |Ex f + |Ez f =

= 4-^cos a cos ( kx sin a ) - cos ( ky sin a ) ] +        (4)

+ sin² a sin² ( kx sin a ) } .

При сложении четырёх плоских волн под большим углом ( a ^ п /2), вместо (4) приближённо можно записать:

I _{п /2} ~ 4 ( cos² ky + sin² kx ) .                           (5)

Из (5) видно, что максимумы интенсивности интерференционной картины четырёх плоских волн будут располагаться в шахматном порядке и вблизи точек с координатами:

Г X (2p +1) Xq )

⁽ x p , y ) = 1 — 4— ,— I , p , q = 0, ± 1, ± 2...     (6)

Из (1) и (3) можно также найти проекции вектора Пойнтинга (вектора потока энергии) по известной формуле:

ток энергии выравниваются и приближаются к двум (с разных сторон).

На рис. 2 показаны распределения интенсивности (2 а ) и продольной компоненты вектора Пойнтинга (2 б ) в интерференционной картине четырёх плоских волн (1), (3) на расстоянии z =0 и при угле схождения α, равном 70° градусов. Картины на рис. 2 рассчитаны с помощью строгого решения уравнений Максвелла FDTD-методом.

S = -Re Г е X H * 1 ,

2 L ]

где Re – действительная часть числа, * – знак комплексного сопряжения. Подставляя (1) и (3) в (7), получим для продольной компоненты вектора Пойнтин-га выражение:

S z , _a = 2 cos a[ cos²( kx sin a ) + cos²( ky sin a ) ] -

- 2 ( 1 + cos² a ) cos( kx sin a ) cos( ky sin a ).

Из (8) видно, что при малом угле схождения ких волн (a ^ 0) обратного потока нет, так как

S z , _a ^ o ~ 2 [ cos( kx a ) - cos( ky a ) ] 2 >  0.

(8) плос-

а)

А при большом угле сложения плоских волн ( a ^ п /2) из (8) следует, что в интерференционной картине в шахматном порядке расположены области, в которых световая энергия течёт в обратном направлении:

S z ,a^/2 = - 2cos ( kx ) cos ( ky ).

Из (10) следует, что максимальные значения обратного потока энергии в сечении картины интерференции четырёх плоских волн находятся вблизи точек с координатами:

( x p , y q ) = ( X p , X q ),   p , q = 0, ± 1, ± 2...

б)

⁽ x p , У ч ) =

X

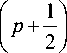
X

1 11 q + 2 11,

p , q = 0, ± 1, ± 2...

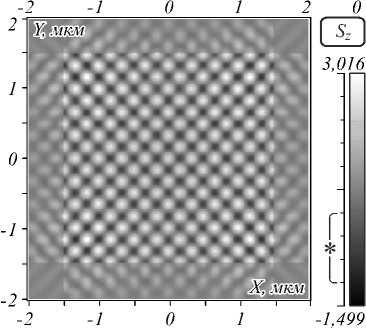
Рис. 2. Распределение интенсивности (а) и продольной компоненты вектора Пойнтинга (б) для четырёх плоских волн (1), (3) с углом сложения α, равным 70°, и для длины волны 633 нм. Тёмно-серым цветом (б, на шкале отмечен знаком «*») показаны области обратного потока

Заметим, что при любом угле схождения a в центре картины интерференции на оптической оси интенсивность отлична от нуля и поток энергии отрицательный:

I _a ( x = У = 0) = 4(1 - cos a )², S z , a ( x = У = 0) = - 2(1 - cos a )².

Максимальный прямой поток энергии в интерференционной картине равен:

_ Г     X (2 p + 1)      X (2 q ) 1

S z _a| x =---------- , x =-------1 = 2(1 + cos a )². (13)

V 2sin a 2sin a I

Выражение (13) верно также для точек с координатами:

Xp       X( q +1/2)

sin a        sin a

При стремлении a к п /2 максимальный прямой поток энергии и максимальный по модулю обратный по-

Из (7) следует, что поперечные составляющие вектора Пойнтинга равны нулю. То есть картина интенсивности и распределение потока энергии на рис. 2 будут одинаковыми при любом z .

Как следует из (1), (3) и (7), тройка векторов S , E , H на оптической оси ( x = y =0) является не правой, а левой тройкой, что означает, что поток энергии и волновой вектор k направлены в обратную сторону по отношению к направлению оси z . Действительно, на оптической оси имеем (рис. 1):

E ( x = у = 0) = E ₁ + E ₂ + E ₃ + E 4 =

= - 2 e _x (1 - cos a ) exp( ikz cos a ),

H ( x = у = 0) = H 1 + H 2 + H 3 + H 4 =            (14)

= 2 e _y (1 - cos a ) exp( ikz cos a ),

S ( x = у = 0) = - 2 e _z (1 - cos a )².

Для наглядности на рис. 3 показана правая тройка единичных векторов декартовых координат ( e x , e y , e z ) и левая тройка векторов S = c k , E , H на оптической оси.

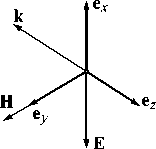
Рис. 3. Правая тройка декартовых единичных векторов и левая тройка векторов k , E , H светового поля на оптической оси

Формирование обратного потока на оптической оси в фокусе светового поля с поляризационной сингулярностью

Здесь и далее мы будем называть поляризационным вихрем световое поле с поляризационной сингулярностью произвольного порядка. В этом параграфе мы покажем, что аналогично формированию обратного потока при интерференции четырёх плоских волн можно объяснить формирование обратного потока в фокусе поляризационного вихря (т.е. поля с поляризационной сингулярностью). В [14] рассмотрена острая фокусировка поляризационного вихря, начальный вектор Джонса которого имеет вид (рис. 4) ( ф - азимутальный угол цилиндрической систем координат ( г, ф , z )):

- sin2 ф        - cos2 ф

E = 1 I, H = 1( cos2фJ      (-sin2ф

На рис. 4 а показано распределение векторов поляризации в поляризационном вихре второго порядка (длина волны X = 532 нм), который фокусировался апланатической системой с числовой апертурой NA=0,95. На рис. 4 б показано распределение интенсивности вблизи фокуса в плоскости ( y , z ) и стрелками показано направление потока энергии S .

С помощью формул Ричардса – Вольфа в [14] показано, что в плоскости фокуса поля (15), сформированного апланатической оптической системой (идеальной сферической линзой), проекции электрического и магнитного векторов имеют вид:

E x = - i sin 2 ф I о,2 ,

E y =- i (^{- cos2 ф} I 0,2 ⁺ I 2,0 ) ,

E_z = 2sin ф 1 1,1 ,

H x =- i ( cos2 ф 1 0,2 + 1 2,0 ) ,

H_y = - i sin 2 ф 1 ₀ , ₂, H_z = 2cos ф I !,1 .

y,

5,

2,

-2,

-5,

а)

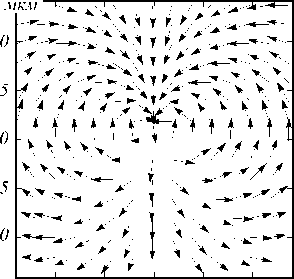
Рис. 4. Распределение векторов поляризации в начальном поляризационном вихре второго порядка (15) (а) и распределение интенсивности вблизи фокуса в плоскости (y, z) (б). Стрелками на (б) показано направление потока энергии S

б)

В (16) использованы обозначения:

n f ^а

I_{o 2} =   f Sin 0 cos¹ / ² 0 (1 + cos 0 ) A ( 0 ) X

’ X 0

x e ikz cos ⁰ j 2 ( x ) d 0 ,

Пf a

1 ₂ , ₀ = — f sin 0 cos¹ / ² 0 (1 - cos 0 ) A ( 0 ) x          (17)

x e ikz cos ⁰ j 0 ( x )d 0 ,

nf a

I ! =   J sin² 0 cos¹ / ² 0 A ( 0 ) X

’ X 0

x e ikz cos e j 1 ( x )d 0 .

В (17) x = kr sin 0, Jm (x) - функция Бесселя m-го порядка, Am (0) - действительная функция, описывающая распределение амплитуды во входном зрачке апланатической системы, NA = sin а и f - числовая апертура и фокусное расстояние апланатической си- стемы. Из (16) следует, что в плоскости фокуса (z =0) на оптической оси поле описывается левой тройкой векторов:

E = - i e y I 2,0 , H = - i e x I 2,0 , S = - e z I 2,0 . (18)

Тройка векторов (18) (без учёта мнимой единицы, которая показывает скачок фазы поля на п /2 в фокусе) аналогична тройке векторов (14) и показывает, что поток энергии на оптической оси обратный по отношению к направлению оси z (рис. 4 б ).

На рис. 5 показаны рассчитанные с помощью FDTD-метода распределение продольной компоненты вектора Пойнтинга Sz в плоскости XZ вблизи фокуса поляризационного вихря второго порядка (рис. 4а) и распределение напряженностей электрического и магнитного векторов на оптической оси (рис. 4б). Из рис. 5б видно, что, хотя световое поле распространяется вдоль положительного направления оси z (слева направо на рис. 5б), вектора E и H вблизи оптической оси складываются таким образом, что об- разуют левую тройку векторов (вместе с волновым вектором k), как будто световая волна на рис. 5б бежит в обратном направлении. Чтобы убедиться, что этот обратный поток имеет физический смысл, в следующем параграфе рассчитаны силы, действующие на рэлеевскую наночастицу, помещенную на оптическую ось вблизи фокуса (рис. 4б и рис. 5а).

а)

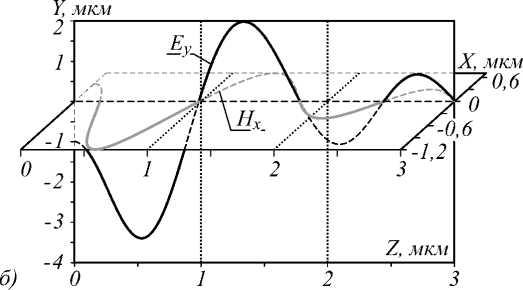
Рис. 5. Распределение продольной компоненты вектора Пойнтинга S z в плоскости ZX вблизи фокуса поляризационного вихря (рис. 4), рассчитанное FDTD-методом (a), и распределения вдоль оптической оси электрического и магнитного полей E y , H x (б)

Сила, действующая на наночастицу в обратном потоке

При размещении частицы в световом поле на частицу действует сила. Для рэлеевской частицы эта сила складывается из рассеивающей и градиентной сил. Для рэлеевских частиц с радиусом a <  X /20, помещённых в световое поле, сила рассеяния F s и градиентная сила F g рассчитываются по известным формулам [34]:

(х /_ х 2

8Пn2 I И^6 I n2 — n2 I --------I k a II

3 c J     ^ n 1² + 2 n 2 J

I

^n- |a31 _П2-П2_ IvlEl2,(20)

, c J ^ n2 + 2 n 2 J где c – скорость света в вакууме, a – радиус сферической рэлеевской частицы, n1 и n2 – показатели преломления частицы и среды. Рассчитывая продольную компоненту вектора Пойнтинга Sz и градиент интенсивности V|E|2 вблизи фокуса поляризационного вихря по формулам (16), (17) и затем рассчитывая рассеивающую и градиентную силы для частицы с радиусом а =10 нм (X = 532 нм) и показателем преломления n1 = 1,5 (n2= 1) по формулам (19) и (20), получим зависимости сил от продольной координаты (частица смещается вдоль оптической оси z), показанные на рис. 6а. Мощность исходного пучка – 100 мВт. Числовая апертура при фокусировке NA=0,95. Из рис. 6а видно, что сила рассеяния больше градиентной силы и направлена против оси z (то есть продольная проекция вектора силы отрицательная). Под действием этой силы частица будет двигаться в отрицательном направлении вдоль оси z. Для сравнения на рис. 6б показаны сила рассеяния и градиентная сила, действующие на ту же наночастицу, но помещённую в острый фокус плоской волны с линейной поляризацией (при прочих равных условиях). Видно, что частица под действием силы движется в положительном направлении оси z. Заметим, что величина силы (в пиконьютонах) на рис. 6б по порядку величины совпадает с силой, действующей на аналогичную наночастицу в фокусе Гауссова пучка, рассмотренную в работе [34].

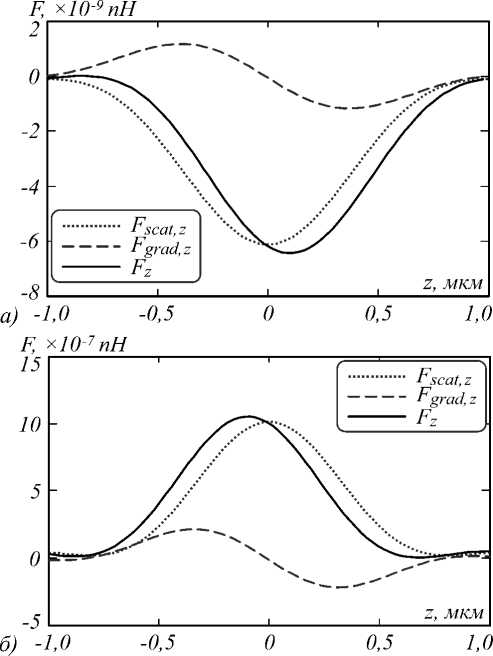
Рис. 6. Продольные проекции силы рассеяния (пунктирная линия), градиентной силы (разрывная линия) и суммарной силы (сплошная линия) вдоль оптической оси (r=0) для частицы радиусом 10 нм с показателем преломления 1,5, помещённой на оптическую ось вблизи фокуса поляризационного вихря (рис. 4б) (а) и в фокусе плоской волны с линейной поляризацией (б)

Заключение

В работе теоретически показано, что в интерференционной картине четырёх плоских волн со специально подобранными направлениями векторов линейной поляризации формируется обратный поток энергии. Области прямого и обратного потока перемежаются в шахматном порядке в сечении интерференционной картины. Величина обратного потока прямо зависит от угла схождения плоских волн (от угла между волновым вектором и оптической осью) и максимальна при угле схождения, близком к 90 °. Правые тройки векторов четырёх плоских волн k (kz > 0), E, H (волновой вектор и вектора напряжённостей электрического и магнитного полей) при сложении в некоторых областях интерференционной картины формируют электромагнитное поле, описываемое левой тройкой векторов k (kz <0), E, H. В этих областях свет распространяется в обратном направлении. Аналогичное объяснение механизма формирования обратного потока можно применить и к случаю острой фокусировки поляризационного вихря второго порядка (рис. 5б). Также показано, что если в область обратного потока поместить сферическую диэлектрическую рэлеевскую наночастицу, то на неё будет действовать сила, направленная в обратном направлении (при этом рассеивающая сила будет больше градиентной).

Работа выполнена при поддержке Российского научного фонда (грант 17-19-01186) в части «Сила, действующая на наночастицу в обратном потоке», Российского фонда фундаментальных исследований (грант 18-29-20003) в части «Формирование обратного потока на оптической оси в фокусе поляризационного вихря» и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение 007-ГЗ/Ч3363/26) в части «Интерференция четырёх плоских волн с линейной поляризацией».