Механизм генерирования и распространения вибрации в технологических машинах

В последние годы заметно оживился темп роста освоения новых изделий ракетно-космической техники, сопровождающийся вводом в эксплуатацию прогрессивных средств технологического оснащения (СТО) и модернизацией существующего парка технологических машин. При анализе мировых показателей конкурентоспособности СТО по пяти направлениям – точность, надежность, производительность, удобство обслуживания, безопасность работы – важное место занимают вопросы оценки вибрационных процессов, понимания и объяснения механизма генерирования вибрации в рабочих машинах.

Технологическая постановка задачи. Раскрытие механизма генерирования вибрации в СТО расширяет эффективность их использования, заключающуюся в обеспечении рациональных режимов обработки заготовок по условию минимизации амплитуд компонент вибрации. В технологических системах наибольший интерес представляет степень влияния вибрации на шероховатость и точность обработки.

Основными причинами возбуждения вибрации в СТО являются режимы резания и подачи, особенности конструктивного исполнения режущего инструмента и СТО [1]. При этом значительную роль играют неравномерные вращательные и (или) поступательные движения рабочих валов и суппортов, эксцентриситет между осью вращения шпинделя с режущим инструментом и осью, проходящей через центры элементарных подвижных и вращающихся масс, принадлежащих базовым механизмам.

Физическая постановка задачи. В технологических машинах, работающих со стружкообразованием и без него, в процессе работы возникают разнообраз- ные механические неуправляемые движения в форме поперечных, угловых, случайных колебаний. Установление механизма и концептуальных причин возникновения колебательных процессов в рабочих машинах является тем фактором, который позволяет активно управлять параметрами вибрации. Это особенно важно на стадиях анализа и формирования проектных решений, разработки конструкторской документации конкурентоспособной продукции.

Физико-механические свойства материалов определяются химическим составом и строением их атомов. Орбитальная скорость движения электрона 106 м/с согласуется со скоростью распространения упругих волн деформации в металле 6,7·103 м/с [2].

При взаимодействии между положительными ионами и отрицательными коллективизированными электронами действуют электрические силы притяжения, стягивающие между собой ионы. Частота колебаний атомов порядка 1013 Гц [3].

Математическая постановка задачи. Механика технологических процессов формообразования контура деталей базируется на математических началах Ньютона и Лагранжа, базовой теории малых колебаний. Конструкции СТО обладают жесткостью, массой, упругостью динамической системы, характеризующими вибрационные процессы и входящими в дифференциальные уравнения движения. При определенных условиях вибрация может быть опасной для конструкций по признакам разрушения и вредной с точки зрения снижения качества и производительности обработки. Основной задачей в теории управления динамики работы СТО является удержание и снижение амплитуды компонент вибрации в допустимых пределах.

Аподиктические признаки задачи управления вибрационными явлениями в СТО базируются на логической необходимости раскрытия связи явления вибрации в технологических машинах на основе использования физической сути явления.

О равновесии системы можно судить по характеру движения после выведения ее из равновесного состояния. При колебательном движении система может быть устойчивой и неустойчивой. При одновременном действии восстанавливающих и возмущающих сил механическая система совершает сложное колебательное движение с двумя составляющими: гармоническим свободным колебанием и вынужденным колебанием. При свободных колебаниях амплитуда и начальная фаза колебаний являются произвольными и постоянными, определяемыми по начальным условиям; а при вынужденных колебаниях дифференциальные уравнения движения не содержат произвольных постоянных и не зависят от начальных данных. Частота и период вынужденных колебаний совпадают с частотой и периодом изменения возмущающей силы. При этом если вынужденная частота меньше частоты свободных колебаний, вынужденные колебания и возмущающая сила находятся в одинаковых фазах и с ростом вынужденной частоты растет и амплитуда колебаний. Если вынужденная частота больше частоты свободных колебаний, тогда вынужденные колебания и возмущающая сила находятся всегда в противоположных фазах. В этом случае с увеличением вынужденной частоты амплитуда колебания уменьшается, это важно для СТО, работающих со стружкообра-зованием. Амплитуда вынужденных колебаний зависит от значения модуля нагрузки и от изменений вынужденной частоты силы.

В общем случае амплитуда вынужденных колебаний может быть оценена рядом известных уравнений, представленных в ГОСТ 24347–80.

В дифференциальное уравнение движения упругой системы входят силы инерции, сопротивления, упругости и возмущения [4]:

mq ′′ +α q ′+ cq = F ⋅ sin ω t , (1) где m – масса; α – коэффициент сопротивления; с – жесткость; ω – вынужденная частота.

Обобщенная возмущающая сила равна n

F = ∑ ( F ix dx i / dq + F iy dy i / dq + F iz dz i / dq ), (2) i = 1

где F ix , F iy , F iz – проекции силы F i на оси x i , y i , z i декартовых координат. Сопротивление увеличивает период свободных колебаний, затухание колебаний при этом идет интенсивнее.

Приведенное уравнение движения в обобщенных координатах, записанное в форме ускорения, имеет вид q′′ + 2hq′ +p2q=Hj ⋅sin ωt, (3) где h – коэффициент демпфирования; р – частота собственных колебаний; Н – приведенная нагрузка.

Решение уравнения движения дает закон движения исследуемой упругой системы.

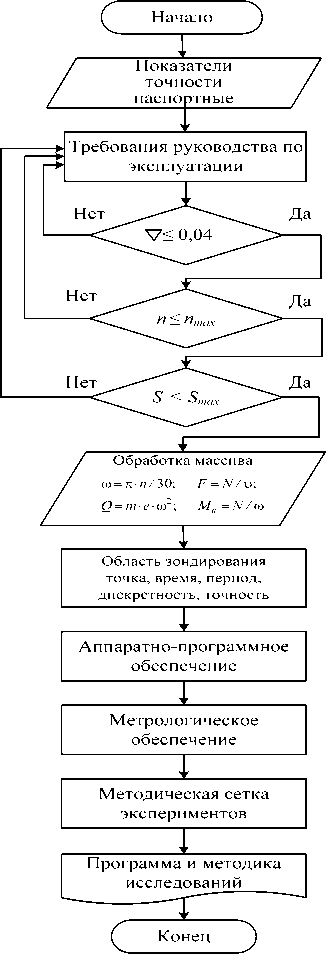
Рис. 1. Феноменологическая модель исследования вибрации рабочей машины

Уравнения угловых колебаний в обобщенных координатах имеют вид

Iψ′′+βψ′+ Cψ =M⋅sin ωt, ψ′′+2ξψ′+χ2ψ=T⋅sin ω⋅t, (4)

где I – момент инерции твердого тела; β – коэффициент сопротивления при угловых колебаниях; ξ – коэффициент демпфирования для угловых колебаний.

Приведенные компоненты вибрации в процессе исследования, как правило, регистрируются стандартной измерительной аппаратурой, например, переносным виброметром типа СМ 3001 или модели АТТ 9002 [5].

Начало

Чертеж детали, СБ

ДФР, ТУ, ТТ, m

Заготовка

Техпроцесс

Режим обработки

Контроль

КИМ

1
Ra, ±, //, ©, О, /r , И	3 Деталь
±, //, ©, ^, j, e, ©, HB	4 Сборка
	5
/ r, Z r , ±, //V , О, j	Регулировка
/ r , a v , V v , L v , S v , e	6 Обкатка
/ r , L v , a v , V v , ©, m	7 Юстировка
0,6 ГТ, ТТ, ПТ	8 ПСИ, КВИ

Нет

Доработка

Д01

СТО, ТЗ, НТиЖ, V v , режимы обработки

Техпроцесс

F = m · e ·ω²

300 тестовых испытаний, HAAS

Стенд

ИСО 230.8–2009

Нет

Оснастка

T k > 0; ω > 0

7,24 = 168 ч

Дефектация

Режим обработки

Замена комплектации

Д02

Ревизия сборок

Д03

Регулировка

Д04

Да

Оформление РЭ, ПС

11

Упаковка

12

Рынок НТх и ВТ

Упругая системa

b
	a

ПСИ

Д05

ТЗ

Д06  Нет

Да

РЭ, ПС

Д07

Д08

Упаковка

Д09

Типовые испытания

Изменение КД

Патент, know-how

М02

М03

М04

Новая модель

М01

∆ j ∆ r в ∆ r a ±, А// ∆ V v

∆ a ∆ L

v

v

∆ S v ∆ V ∆ω

z		j
^a		∆НВ
^ e		∆ σ в
^ Y		∆ Т
^ ф		∆ A ο кр
ПТС		Стар
∆ T		ТДП
∆ j		Fe 2 O 3
Гиб		FeO
Т		∆Н 2
		∆ p
		Зерно
		изн

Рынок, 0,8 цены

СТО

МРИ

Материал

Рис. 2. Технологическая модель генерирования вибрации в технологической машине

На основе фундаментальных уравнений малых колебаний разрабатываются алгоритмы исследования, измерения и регистрации компонент вибрации с их параметрами: амплитудой, частотой и периодом. Базовым документом при выполнении физического измерения может послужить технический регламент ISO/TR 230-8–2009 « Свод правил по испытанию станков. Часть 8. Оценка уровней вибрации».

Разработка феноменологической модели. Изложение и решение задачи раскрытия механизма генерирования вибрации начинается с представления и анализа феноменологической модели [6] (рис. 1).

При этом выполняется теоретическая проработка рабочей документации СТО с оценкой величин геометрической, технологической, параметрической точности и параметров, входящих в техническую характеристику; определяются конкурирующие технологические показатели режима и динамики базового процесса; выполняется первичная привязка измерительных устройств к объекту исследования.

Руководствуясь феноменологической моделью, строится технологическая модель исследования механизма генерирования вибрации (рис. 2), например, в процессе изготовления товарной продукции в виде детали.

На рис. 2 приняты следующие условные обозначения: ДФР – допуск формы и расположения поверхностей; ТУ – технические условия; ТТ – технические требования; m - масса; Ra - шероховатость; | - допуск перпендикулярности; / - допуск перпендикулярности; © - допуск соосности; ^V - допуск плоскостности; ^ r -радиальное биение; /^ - допуск цилиндричности; // - полное биение; j - жесткость системы; e - эксцентриситет; ф - точность позиционирования; HB – твердость. z_r – радиальный зазор;

– установка по уровню, мм/м; av – виброускорение; Vv – виброскорость; Lv – логарифмический уровень акустических характеристик; Sv – виброперемещение; 0,6 ГТ – сдаточные нормы геометрической точности; ТТ – нормы технологической точности; ПТ – нормы параметрической точности; СБ – сборочный чертеж; ПСИ – приемосдаточные испытания; КВИ – контрольно-выборочные испытания; СТО – средства технологического оснащения; ТЗ – технического задание; НТиЖ – нормы точности и жесткости; РЭ – руководство по эксплуатации; ПС – паспорт; НТх и ВТ – новая техника и высокие технологии; КД – конструкторская документация; Tk – кинетическая энергия; ω – вынужденная частота; 7,24 = 168 ч – типовые испытания; КИМ – коэффициент использования материала; 0,8 цены – реализация по себестоимости; ИСО 230.8–2009 – международные стандарты по испытаниям станков; Д01–Д09 – доработка; М01–М04 – метрологическое обеспечение. Для СТО (средств технологического оснащения): ∆j – отклонение от жесткости; ∆ra и ∆rв – погрешности передней и задней опоры; | - допуск перпендикулярности; А/ - отклонение от параллельности; AVv - отклонение от виброскорости; ∆av – отклонение от виброускорения; ∆Lv – отклонение от логарифмического уровня; ∆Sv – отклонение от виброперемещения; ∆V – отклонение от скорости; ∆ω – отклонение вынужденной частоты. Для МРИ (металлорежущего инструмента): z - число зубьев; ^а, ^в, ^У, ^Ф - углы режущей кромки инструмента; ПТС – пластины твердосплавные; ∆T – стойкость инструмента; ∆j – отклонение от жесткости; Гиб – гибкость; Т – температура. Для материала: j – жесткость; ∆НВ – разброс твердости; ∆σв – отклонение от предела текучести; ∆T – температуростойкость; ∆Aοкр – эффект старения; Стар – старение; ТДП – термодинамические процессы; Fe2O3 – формирование пленок; Н2 – водоражива-ние; ∆p – погрешность плотности; Зерно – зернистость; Iизн – параметр износа.

По результатам проработки формируется структура, программа и методика испытаний СТО, класс точности измерительных приборов для получения результатов испытаний не ниже 3-й степени точности при 2-м классе точности приборов, регламентированных техническими регламентами серии ИСО 230.

Анализ рабочих и сборочных чертежей изделия, технических условий и входящих технических требований заканчивается разработкой маршрутного и операционного технологических процессов.

Сложный процесс формирования механизма генерирования вибрации в технологических системах представлен в виде развития цепной реакции (рис. 3), впервые рассмотренной академиком Н. Н. Семеновым для процесса горения.

На рис. 3 приняты следующие условные обозначения: – точки и область зондирования компонент вибрации при экспериментальных исследованиях; e _э(ω) – градиент скорости изменения магнитного зазора, шага зубцов, напряжения питания электродвигателя привода первого механизма, подлежащего пуску для начала работы; e ск – параметры собственных колебаний системы, а также характеристики внешних факторов окружающей среды по сейсмичности; e Мх (ω) – градиент изменения угловой скорости якоря электродвигателя от влияния зазора в опорах, соосности, радиального биения; e M (p) – вариация собственной частоты колебания двигателя от изменения электромагнитных и электромеханических постоянных времени двигателя; e c (ω) – характеристика жесткости; e_m (ω) – влияние элементарных подвижных масс системы; e_l (ω) – влияние линейно-угловых размеров конструкции механизмов; e_y (ω) – статический и динамический прогиб рабочих валов; e перед (ω) – e вал (ω) – градиенты амплитуд вибрации вращающегося вала; e подш (ω) – амплитуда вибрации в подшипниках базовых механизмов; e ω (ω) – изменение частоты вращения рабочего вала от вариации динамических нагрузок; e рег (ω) – удельный регламентированный дисбаланс подвижных масс; e посад (ω) – характер изменения посадки опоры; ∅ T рс – влияние соосности вращающихся валов; e ( p ) – вариация частоты собственных колебаний технологической системы; e РИ (ω) – градиент амплитуды от способа и точности подготовки режущего инструмента; e_z (ω) – влияние шага зубьев режущего инструмента на формирование ударных явлений;

e β (ω) – влияние контурных и динамических углов на силы сопротивления резанию; e _износ(ω) – влияние износа на траекторию движения исполнительных органов; e Тh (ω) – изменение постоянной времени демпфирования материала инструмента и упругой системы машины; e TK (ω) – изменение амплитуды тел качения в опорах от точности их изготовления; e кп (ω) – вариация амплитуды колебания колец подшипника; G 2, G 6 – регламентированные классы точности балансировки рабочих валов; e да (ω) – вариация размеров детали; e V p (ω) – вариация скорости резания; e F (ω) – изменение сил сопротивления резанию; e_n (ω) – изменение частоты вращения от режимов резания; e _μ1(ω), e μ2 (ω), e μ3 (ω), e μ4 (ω), e μ5 (ω), e μ6 (ω), e μ7 (ω), e μ8 (ω), e μ9 (ω) – градиент амплитуды колебания молекул, атомов, ионов в материале от действия технологических факторов, вызывающих деформации и изменения температуры.

По методологии анализа цепных процессов проблемная задача раскрывается ее решением по трем направлениям начала образования механизма и развития процесса вибрации в технических системах.

Первое направление – инициирование процесса вибрации; второе – развитие процесса; третье – стабилизация процесса.

Во всех направлениях прорабатываются критерии минимизации необходимого и достаточного условия активного управления градиентом базовой характеристики процесса вибрации конструкции СТО:

lim[grad( e ·ω)] = min; lim[grad( m · e ·ω²)] = min, (5) где е – эксцентриситет оси вращения; ω – угловая скорость рабочего вала; m – масса.

Амплитуда вибрации в работающих механических системах зависит от характера действующих сил и свойств упругой системы. Наиболее интенсивно изменяются параметры вибрации в переходных процессах разгона и торможения базовых механизмов рабочих машин, например, в момент врезания и выхода режущего инструмента из зоны резания.

С момента пуска одного из приводов рабочей машины ее состояние возможно описать дифференциальными уравнениями второго порядка. Процесс вибрации упругой системы рабочей машины мгновенно зарождается при первом же движении привода механизма машины и распространяется по принципу цепной реакции. В качестве оценочного критерия дивергенции вибрационного процесса выбрана функция приведенной скорости упругой системы ( e ·ω).

Упругая система рабочей машины вносит свой вклад в формирование вибрации вследствие вариации жесткости, радиального биения, допусков соосности и перпендикулярности, частотных характеристик, скорости движения, контурных углов резания, термодинамики процесса.

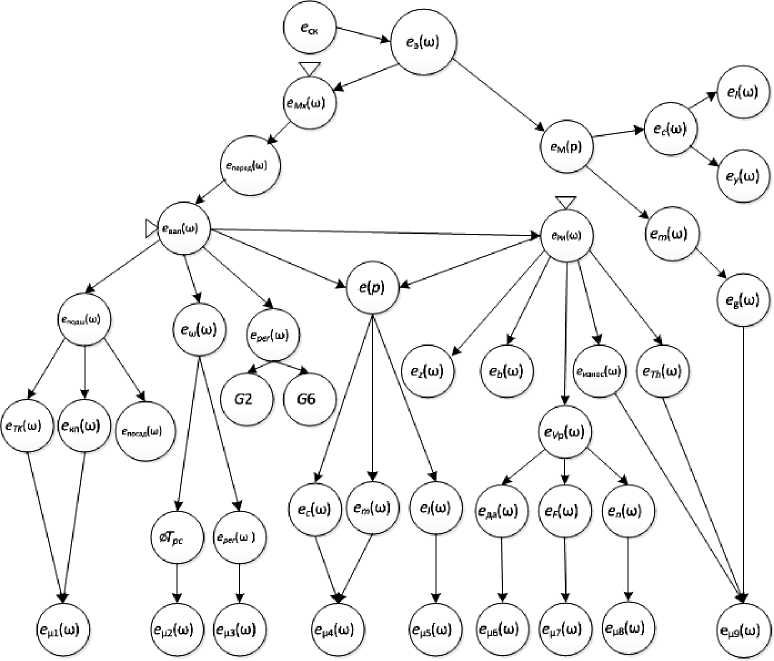
Рис. 3. Характер развития цепной реакции при распространении вибрационного процесса в конструкции рабочей машины

Исследование механизма генерирования вибрации и цепной реакции ее распространения целесообразно выполнять при стендовых испытаниях рабочей машины.

Стендовая обкатка первого рода перед контрольными испытаниями проводится после изготовления изделия для проверки его работоспособности, а также приработки контактных поверхностей. Операция выполняется по специальному регламенту и тестовым программам, позволяющим уточнить механизм генерирования вибрации, цепную реакцию ее распространения. Обкатка второго рода производится в начальный период эксплуатации технологической машины после монтажа в цехе в условиях производства. Приемосдаточные испытания (контрольно-выборочные испытания) выполняются по программе и методике испытаний, где проверяется геометрическая и технологическая точности и анализируется параметрическая точность с установлением фактических величин соответствия ужесточенному уровню значений параметров проверки. В ходе проверки окончательно устанавливается класс точности рабочих машин.

Скорость распространения продольных колебаний в конструкции рабочей машины можно оценить по функции [1]:

V пр = V ( Х + 2 ц )/ р ; Х = E 8 /[(1 - 2 5 )(1 + 5 )];

ц = E /2(1 + 8 ), (6)

где λ, µ – параметры Ламе; ρ – плотность материала; δ – коэффициент Пуассона.

Скорость распространения поперечных колебаний, соответственно, аппроксимируется функцией вида [1]:

Vn = \Ц P •                      (7)

Раскрытие механизма возникновения вибрации на основе математических методов, фундаментальных начал механики Лагранжа и генерирования вибрации в рабочей машине по принципу цепной реакции позволяет создавать управляющие алгоритмы стабилизации режимных параметров технологических процессов.

Частная математическая модель механизма генерирования вибрации в рабочей машине записана в виде функции пиковой виброскорости [7]:

V sp

n • d_t • z 60 • ( d e - df)

N IT

[n • {[^ J dx / (kr • x + kl)] / N + rt=1 0

M it                                              nk

+ [ ^J dy /( k l • y + k r )]/ M }/2] + —-• ( £ X i ) rb =1 ₀                                       ⁿk ¹ i =1

где V sp – виброскорость в локальной энергонасыщенной интегральной точке механизма главного движения; d i , z – параметры опор качения; n – частота вращения; it , IT – допуски на размеры контактных пар; х_i – составляющие компоненты виброскорости, которые определяются по частным функциям, описывающим допуски в подвижных контактных парах, кинематические связи, эксцентриситет и соосность, динамические прогибы в рабочих валах.

При анализе механизма генерирования вибрации особое внимание следует обращать на технологии разработки и производства машин. Исходными документами для решения поставленной проблемной задачи – раскрытия механизма возникновения вибрации – являются: технические условия на изделия, отечественные и зарубежные технические регламенты, патенты и ноу-хау, рабочие чертежи деталей и сборок, типовые технологические процессы.

Таким образом, можно сделать следующие выводы:

• 1.    Механизм генерирования и распространения вибрации в технологических машинах, построенный на принципах теории цепной реакции, наиболее точно отвечает физическому процессу действия вибрации на точность формирования контура деталей. Генерация вибрации в рабочей машине начинается с момента пуска двигателя привода первого механизма и распространяется по принципу цепной реакции со скоростью не выше 6,7·10³ м/с.

• 2.    Раскрытие механизма возникновения вибрации на основе математических методов описания технологического процесса, построенных на фундаментальных началах Ньютона и Лагранжа, генерирования и распространения вибрации в рабочей машине по принципу цепной реакции позволяет создать новые управляющие алгоритмы стабилизации режимных параметров вибрации технологических процессов.

• 3.    Созданная на основе феноменологической модели исследования вибрации рабочей машины, технологическая модель генерирования вибрации в технологической машине раскрывает значимость параметров геометрической, технологической и параметрической составляющих показателей точности и их влияние на динамику процесса резания материалов.

• 4.    Микроколебания в материалах механизмов на уровне атомно-молекулярного строения не оказывают существенного влияния на вибрацию станка. Однако изменение постоянной времени демпфирования и динамической вязкости материала в процессе работы станка подтверждает степень влияния металлических и химических связей между атомами, ионами и коллективизированными электронами, свидетельствующего о непостоянстве сил сопротивления, входящих в дифференциальное уравнение колебаний материальной точки.

• 5.    Величина эксцентриситета оси вращения с осью, проходящей через центры вращающихся масс, большей частью формируется конструктивными решениями и, как следствие, технологическим процессом изготовления деталей, включая операцию динамической балансировки роторов.