Механизм ионной проводимости твердого электролита LiPON

Твердотельные тонкопленочные литий-ионные аккумуляторы относятся к сравнительно новыми перспективным химическим источникам энергии. В подавляющем большинстве таких аккумуляторов в качестве твердого электролита используется фосфор-оксинитрид лития (LiPON). Важнейшие характеристики LiPON были изучены еще в середине 90-х его разработчиками Дж. Бейтсом и др. [1-7]. Эти работы стали классическими и более поздние исследования опираются на их результаты. В частности, в работе [5] было получено значение проводимости σ = 2.3 ⋅ 10-4 S ⋅ m-1, которое стало практически критерием достоверности результатов других авторов. В то же время параметры структурной модели LiPON, приведенные в [5], позволяют усомнится в правильной интерпретации именно этого параметра.

На рисунке 1 приведена структурная модель LiPON, которая использовалась в работе [5] для аппроксимации диаграмм Боде.

Рис. 1. Эквивалентная схема тестовой структуры Pt|LiPON|Pt, где R el и R r – активное сопротивление электролита и реактивного слоя соответственно, Z el и Z r – элементы постоян-

ной фазы. Z i – импеданс интерфейса Pt|LiPON|Pt, C g – «геометрическая емкость» тестовой структуры [5]

Здесь R el и R r – активное сопротивление электролита и реакционного слоя. Элементы Z el , Z r и Z i , моделируют импеданс электролита, реакционного слоя и интерфейсов

Pt|LiPON|Pt соответственно. Символом Z в работе [5] используется для обозначения элементов постоянной фазы (CPE)

Z = A(j ω ) ^-α ,

где A – постоянная, ω – циклическая частота, а α – фактор неидеальности. Элементы R r и Z r , описывающее реакционный слой, имеют смысл только при напряжении смещения более 5 V, поэтому далее не рассматриваются. Чтобы оценить степень адекватности структурной модели реальной системе необходимо определить физический смысл основных структурных элементов и оценить их параметры.

Элемент Z i при α = 0.96 ÷ 0.98 имеет смысл неидеальной емкости с небольшим протеканием. Для значений A_i = 1.3 ⋅ 10⁶ и α о 1 емкость элемента Z i составляет достаточно большую величину C_i = 0.77 µ F . Такая емкость характерна для плотного двойного электрического слоя (ДЭС). При площади контакта S = 4 ⋅ 10 ^{- 6} m ² толщина слоя в рамках модели Гельмгольца составляет 0.46 ⋅ 10 ^{- 10} m . Обычно ДЭС с протеканием описывается схемой Рэндлса, изображающей емкость с параллельным ей сопротивлением утечки. Это сопротивление моделирует редокс процессы, которые определяют величину тока утечки. В [5] схема Рэндлса заменяется введением неидеальной емкости Z i для которой α< 1 . Но в этом случае утечка имеет диффузионную природу, в то время как протекание ДЭС не может происходить иначе, как через редокс процесс. Другими словами, это не тот механизм утечки, который моделирует схема Рэндлса.

Элементы Z el и R el моделируют диффузионный и дрейфовый перенос ионов лития. В работе [5] при нулевом смещении эти параметры имеют значения

R el = 3.7 ⋅ 10³ Ω , A = 3.1 ⋅ 10 ⁷ Ω⋅ s ^-α и α= 0.66 . Последний параметр указывает на то, что элемент Z достаточно близок к диффузионному элементу Варбурга. Импеданс Варбурга Z = A_W (1 - j) / ω , где A W = A/ 2 – коэффициент (амплитуда) Варбурга, получается из элемента постоянной фазы Z = A(j ω ) ^-α при α= 1 / 2 . То обстоятельство, что α> 1 / 2 означает, что элемент Z_el не является чисто диффузионным, а имеет некоторую емкость.

На частоте ω 103 , которой соответствует локальный минимум мнимой части импеданса Pt|LiPON|Pt [5], величина Re Zel = Aelω-α cos(απ / 2) составляет 1.6 ⋅ 105 Ом , что на два порядка больше R . Из чего можно заключить, что в LiPON преобладает дрейфовый механизм переноса заряда. Однако это противоречит сразу двум фактам. Во-первых, при полученной выше толщине ДЭС поле внутри электролита ослаблено на четыре порядка и перенос заряда не может быть преимущественно дрейфовым. Во-вторых, полученное Дж. Бейтсом и др. значение проводимости σ = 2.3 ⋅ 10-4 S ⋅ m-1 дает очень высокое значение концентрации подвижных ионов лития. В рамках теории Друде концентрацию ионов можно рассчитать, как c=σkBT/Dq2, где D – коэффициент диффузии ионов лития. Для значения D 10-15 м2 ⋅ с-1 [8] и проводимости σ = 2.3 ⋅ 10-4 S ⋅ m-1 концентрация ионов составляет c =2,5 ⋅1028 m-3 , т.е. сопоставима с концентрацией атомов в металлическом литии c =4, 6 ⋅1028 m-3 . Если же учесть ослабление поля внутри LiPON на четыре порядка, то проводимость, а соответственно и концентрация должны быть еще выше. Очевидно, что реальная концентрация ионов лития должна быть несколько ниже полученной величины.

Кроме указанных противоречий, значение σ = 2.3 ⋅ 10 ^{- 4} S ⋅ m ^{- 1} не соответствует данным таблицы II, приведенной в работе [5]. Для сэндвич-структуры Pt|LiPON|Pt с площадью контакта S = 0.04 cm ² , пленки LiPON толщиной 1 мкм и сопротивлением R = 3.7 ⋅ 10³ Ω элементарный расчет дает удельное сопротивление ρ = 1, 48 ⋅ 10⁴ Ω ⋅ m . Соответствующая проводимость составляет σ = 6,8 ⋅ 10 ^{- 5} S ⋅ m ^{- 1}, что меньше приведенного в работе значения. Этому значению проводимости соответствует уже меньшая концентрация ионов лития c = 7,3 ⋅ 10²⁷m ^{- 3} .

Результаты работы [8], в которой использовалась схема Рэндлса (рис. 2), дают значения проводимости 8.7 ⋅ 10 ^{- 5} S ⋅ m ^{- 1}, которое близко к 6,8 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} [5]. Близость полученных значений □ создает впечатление, что этот результат соответствует истинному значению омического сопротивления. Однако это не так. Дело в том, что поле внутри электролита согласно [5] ослаблено на четыре порядка, что эквивалентно увеличению сопротивления на ту же величину. Единственное разумное объяснение сравнительно небольшой величины R _el состоит в том, что это сопротивление току смещения. При колебаниях потенциала на электродах имеет место только изменение концентрации Li⁺ в плотной части ДЭС (слой Штерна) и в его диффузной части. Перемещения ионов в этом случае невелики и ограничены плотными и диффузными слоями ДЭС. При этом сопротивление току смещения не является чисто реактивным, так как при перемещении заряда в пределах ДЭС происходит диссипация энергии. По всей видимости, омическое сопротивление R _el характеризует скорость диссипации энергии, связанную именно с этими процессами.

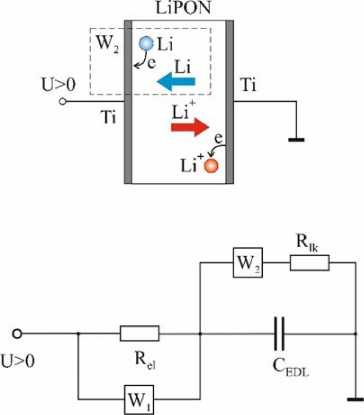
Рис. 2. Структурная модель LiPON. Стрелками показано направление движения зарядов при положительном потенциале на электроде [8]

Для оценки величины сопротивления току смещения достаточно найти отношение напряжения U₀e^{j ω t} к току смещения I = j ω S ε ε ( ω )E e ^{j ω t}

Zdp = δ / jωSε0ε(ω), (2)

где E₀ = U₀/ d , d – толщина LiPON, □ – циклическая частота. Для дебаевской зависимости диэлектрической проницаемости от частоты ε ( ω ) соотношение (2) принимает вид

ˆ         d    ωτ(1 - ρ) - j(1 + ω2τ2ρ)

dp   Sε0ωε(0)       1+ (ωτρ)2       ,

где τ – постоянная времени релаксации поляризации, ρ = ε_∞ / ε (0) . Вещественная часть (3) имеет вид

^{Re Zdp ≈} S ε ₀ ε (0)1 +ω ² τ ² ρ ^{2 .}

Нетрудно убедиться, что при параметрах S = 6.4 ⋅ 10 ^{- 5} m² , ω= 10³s ^{- 1} и τ 0.017s , ε (0) О 10⁴ , ε ∞ п 1 , d = 10 ^{- 6} m , характерных для Pt|LiPON|Pt, ReZ имеет порядок 10³ Ω (табл. 1). Таким образом, Re Z ≈ R и предположение, что R_el – сопротивление тока смещения вполне логично. Далее полученные значения проводимости для тока смещения обозначаются как σ , а именно σ = 6,8 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} (работа [5]), σ = 8.7 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} (работа [8]) и σ = 1.3 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} (настоящая работа).

Таблица 1. Сопоставление параметров структурных моделей LiPON. Все параметры из работы [5] пересчитаны для площади контакта 0,64 см2, как в работе [8]

	R el , Ом	A Wel , □ /s 1/2	С DEL, □ F	Толщина ДЭС по Гельмгольцу, m	□ , S/cm расчет по R el	□ , S/cm по Друде	c, m-3
Бейтс и др. [5]	231,3	~1,9∙106	12	0.47∙10-10	6,8∙10-7	-	7,3∙1027
Работы [8,9]	180,0	1∙104	0,21	2.7∙10-9	8,7∙10-7	-	1,7∙1027
Оценки наст. работы	103	-	-	10-10 – 10-9		1,6∙10-7	-

Приведенные значения σ _dp полезно сравнить с дрейфовой проводимостью LiPON, которая с учетом соотношения Эйнштейна имеет вид σ _dr = Dq²c / kT . Для коэффициента диффузии D = 1.5 ⋅ 10 ^{- 15} m² ⋅ s ^{- 1} [8] и концентрации c = 1.7 ⋅ 10²⁷ m ^{- 3} , полученной в [9], дрейфовая проводимость составляет σ _dr = 1.6 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} (табл. 1). Эта величина оказывается достаточно близкой к значению проводимости

σ = 6,8 ⋅ 10 ^{- 5} S ⋅ m ^{- 1} [5]. Причина, по которой эти параметры близки, состоит в том, что механизмы диссипации импульса ионов в обоих случаях одинаковы. Соответственно значения времени релаксации поляризации импульса также близки.

Результаты анализа работы [5] и ее сопоставления с данными работы [8] позволяют сделать вывод, что экспериментальное значение проводимости обусловлено током смещения. Причина состоит в ослаблении поля, а следовательно, и дрейфового тока внутри электролита. Полученное в [5] значение проводимости ха- рактеризует в основном диэлектрические потери, но никак не способность электролита LiPON переносить электрический заряд, т.е. выполнять основную функцию в составе ТТЛИА. Основными механизмами переноса заряда через электролит является дрейф и диффузия ионов лития.