Механизм сверхразрешения в планарной гиперболической секансной линзе

С помощью ДОЭ совместно с фокусирующей рефракционной оптикой дальнего поля можно достичь сверхразрешения, например, получить фокусное пятно с диаметром по полуспад у интенсивности, равным FWHM = 0,44λ [1], где λ – длина волны света в вакууме, вместо дифракционного предела (FWHM = 0,51λ). Но при этом боковые лепестки дифракционной картины в фокусе буд ут превышать по интенсивности значение 0,1 от величины интенсивности в фокусе. Можно достичь ещё меньшего значения диаметра фокуса в дальней зоне, но при этом будет возрастать доля световой энергии в боковых лепестках так, что их интенсивность может сравниться или превысить интенсивность в фокусе [2]. Заметим, что дифракционных пределов разрешения в оптике известно несколько: это предел разрешения Рэлея 0,61λ / NA [3], предел Хьюстона 0,5λ / NA и предел Спарроу 0,475λ / NA [4], где NA – числовая апертура фокусирующей системы. Мы будем пользоваться своими пределами разрешения, которые определяются для 3D полей по полуспаду квадрата функции Эйри (0,51λ / NA ), а для 2D полей – по полуспад у sinc -функции (0,44λ / NA ).

Чтобы преодолеть предел разрешения без увеличения боковых лепестков, след ует приблизить оптический элемент к источнику света. Эту область оптики исслед ует микроскопия ближнего поля [5]. Если исключить из рассмотрения металлически е поверхности и поверхностны е плазмоны [6], которые позволяют достигать разрешения λ /50, а остаться в рамках рефракционной и градиентной оптики, то высокого разрешения можно добиться с помощью линз ближнего поля: SIL (solid immersion lens) [7], NAIL (numerical aperture immersion lens) [8-10] и nSIL (nano solid immersion lens) [3,11].

С помощью SIL экспериментально для длины волны λ = 633 нм и полусферы из стекла LASFN9 с радиу- сом 5 мм и показателем преломления n = 1,845 было получено разрешение FWHM = 190 нм = 0,298λ [7]. С помощью полусферы из кремния для NAIL радиусом 1,6 мм было экспериментально получено разрешение FWHM = 250 нм = 0,23λ (теоретический предел для кремния FWHM = 0,147λ при n = 3,4 и λ = 1 мкм) [8]. В более поздней работе [9] удалось с помощью кольцевой апертуры и кремниевой NAIL достичь разрешения FWHM = 145 нм = 0,11λ (λ = 1,3 мкм). В случае, если линза освещается кольцевым пучком, то в фокусе формируется Бесселев пучок, для которого предел разрешения равен FWHM = 0,36λ / NA. С помощью оптики ближнего поля (nSIL) на модельных примерах показано, что для полусферы радиусом 1-2 мкм [3] из стекла (n = 1,6) можно получить фокусное пятно диаметром FWHM = 126 нм = 0,235λ (λ = 532 нм) [11]. Заметим, что рефракционная оптика ближнего поля увеличивает числовую апертуру уже сходящегося светового пучка, а при распространении света от источника эта оптика способна только собрать свет, но для фокусировки света требуется дополнительная оптика.

Известны градиентны е линзы ближнего поля, которые способны одновременно и собирать свет от источника, и фокусировать его вблизи своей выходной поверхности. Так, в [12] с помощью моделирования показано, что кремниевая градиентная оптик а ближнего поля (планарная гиперболическая секанс-ная линза) позволяет сфокусировать свет в фокусное пятно с диаметром FWHM = 0,131λ. Это меньше дифракционного предела в 2D среде FWHM = 0,44λ / n = 0,147λ. Было показано также [13], что такая планарная градиентная линза ближнего поля способна разрешить два точечных источника, разделённы х расстоянием 150 нм (λ = 1 мкм), то есть было достигнуто сверхразрешение 0,15λ. Предел разрешения Аббе равен 0,5λ.

В данной работе описывается механизм достижения сверхразрешения с помощью оптики ближне- го поля, в том числе с помощью градиентной планарной линзы. Показано, что часть неоднородных исчезающих волн от точечного источника (поверхностные волны первого типа, k < kx < nk, где k и kx – волновое число в вакууме и проекция волнового вектора на поперечную ось x, n – показатель преломления среды) туннелируют в среду (в линзу), преобразуются в моды этой среды и дают вклад в формирование изображения источника, наряду с обычными распространяющимися волнами (0 < kx < k). В оптике дальнего поля поверхностные волны первого типа не достигают изображения источника. Поверхностные волны источника второго типа (kx > nk) преобразуются в поверхностные волны среды и распространяются вдоль входной поверхности линзы. Выходной поверхности линзы, где формируется изображение, достигают только экспоненциально затухающие «хвосты» этих поверхностных волн.

Получено интегральное представление для ТЕ-вол-ны в 2D среде от точечного источника, находящегося вне этой среды (линия раздела сред – прямая), и аналогичное представление для светового поля за плоскопараллельной пластиной. Произведено также сравнение числовых апертур рефракционных линз ближнего поля (SIL, NAIL) и планарной гиперболической секансной линзы, показано, что они близки межд у собой и отличаются для кремния всего на 5%. Моделированием с помощью программы FullWAVE показало, что добавление к градиентной гиперболической секансой линзе субволновой дифракционной решётки или замена такой линзы её бинарным аналогом приводят к уменьшению ширины фокусного пятна на 10% и 20% по сравнению с дифракционным пределом в данной среде.

то (3) можно выразить через производную ф ункци и Ханкеля:

E ( x , z ) = — ——H 1 ( k4x ² + z ²).

¹ k d z

Пусть на пути излучения, на расстоянии z от источника появляется граница раздела двух сред. То есть излучение от источника проходит в сред у с показателем преломления n . Тогда в среде на расстоянии z от источника амплитуд а электрического вектора будет равна

E ₂ ( x , z ) =

м

= E ₀ J T 1 ( £ ) exp ^— ik L x + ikz 442—L ] d ^ ,

—м

где

24 к

T © = ^

4 1 —^ ² + 4n ² —

² i4 ^ ^{2 — 1}

i4 ^ ² — 1 + 4 n¹ — 2712^1

==, 0 <|^|< 1,

= , ¹ <|^|< n ,

_ 4^2^1 +4^ 2^42

, |^| >  n .

В двумерном (2D) случае напряжённость элек-

трического поля монохроматической ТЕ-волны расстоянии z от начальной плоскости имеет вид:

k +м м

^E 1 ^{( x} , ^z ) =V J I E 0 ⁽ x ', z = ^{0) X}

2n j j

—м —м x exp ^—ik £( x'— x) + ikz 41 — ^2 ] dx 'd^.

Если источник в начальной плоскости точечный:

( kx ^

E o ^{( x} , ^z = ⁰⁾ = E o ⁸ 1— I ,

I 2 n )

на

где 8 ( x ) - дельта-функция Дирака, то амплитуда поля на расстоянии z будет равна сумме плоских волн и неоднородных затухающих волн:

м

Величины T 1 ( ^ ) представляют собой коэффициенты, полученные по формулам Френ еля для трёх различны х случаев: преобразование распространяющейся плоской волны в распространяющуюся плоскую волну; преобразование затухающей плоской волны в распространяющуюся плоскую волну; преобразование затухающей плоской волны в затухающ ую плоскую волну в среде.

Действительно, из (7) видно, что распространяющиеся волны от точечного источника в среде с n = 1 и с 0 <  ^ | < 1, где ^ = k x / k , войдут в среду под углами 0 <  6 <  6 1 , где 6 1 = arcsin(1/ n ), и будут далее распространяться в среде с n > 1. Поверхностные волны первого типа от источника с проекцией волнового числа в диапазоне 1 <  ^ | <  n войдут в среду под углами 6 ₂( ^ ) = arcsin( ^ / n ), лежащими в диапазоне 6 1 <  6₂ © <  п /2, так как максимальный угол 6 ₂ ( ^ ) равен п / 2 при ^ = n . Эти волны, преобразованные из поверхностных затухающих в распространяющиеся, будут и дальше распространяться в среде с n > 1. Оставшиеся поверхностные волны (второго типа) от источника с ^ | >  n будут поверхностными волнами среды и будут распространяться вдоль границы раздела.

м       —                           —■

E 1 ( x , z ) = E 0 J exp I - ik ^ x + ikz 4 1 — ^ 2 I d ^ ■

—м

Заметим, что так как ф ункция Ханкеля нулевого порядка и первого рода имеет вид [14]

H 0 ( k4x ² + z ²) =

Рассмотрим двумерную гиперболическую се-кансную (ГС) линзу, показатель преломления которой имеет вид:

1 м

=П J

—м

exp ^— ik ^ x + ikz 4 1 — ^ 2

d ^ ,

n (x) =

-

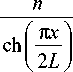
где n – показатель преломления на оси линзы, L – длина линзы, а x – координата в поперечной плоскости.

Числовая апертура ГС-линзы может быть найдена из уравнения луча в градиентной среде: n ( x ) cos 9 ( x ) = const, где 9 - угол между касательной к лучу и оптической осью z . Пусть луч падает на линзу параллельно оптической оси на расстоянии x = R от неё, где R – радиус ГС-линзы, который может быть найден из условия n ( R ) = 1: R = arcch ( n ). Тогда уравнение луча примет вид: n cos 9 0 = n ( R ) cos 9 ( R ) = 1, где 9 0 - угол между касательной к лучу и оптической осью z в точке пересечения луча с осью. Отсюда следует, что cos 9 ₀ = 1 / n , т.е. числовая апертура ГС-линзы 12

равна NA = n sin 9 0 = ( n - 1 ) .

Так как числовая апертура такой линзы равна NA = ( n ² -1)^1/2 = n sin 9 ₀, где 9 ₀ = arcsin [( n ²—1)^1/2 / n ], то плоские волны с углами распространения θ 1 и θ 2 , меньшими θ 0 , будут давать вклад в фокусное пятно на выходе ГС-линзы. Найдём максимальное ξ max для световых волн, которые участвуют в формировании фокуса ГС-линзы. Исходим из равенства 9 2 ( S max ) = 9 ₀, тогда получим arcsin (S/ n ) = arcsin ( n ² - 1 )^/ / n .

Выражение (10) следует из того, что числовая апертура для SIL и NAIL

NA_S L = n sin 9 <  NA NAL = ( n - cos 9 )

в пределе ( 9^ л/ 2) стремится к NA _max = n . Предельное фокусное пятно (10) всего на 5% меньше, чем фокусное пятно ГС-линзы (9). Оценим максимальный угол, под которым распространяются лучи в ГС-линзе. Распространяющиеся плоские волны от источника с относительной проекцией волновых векторов из интервала 0 < | S | < 1 преобразуются в однородной среде ( n = 3,47) также в распространяющиеся волны, идущ ие под углами в диапазоне 0 < 9 < 9 1 = arcsin (V n ) = 17 ° , а максимальный угол

(к оптич еской оси), под которым мог ут распро -страняться лучи в ГС-линзе, рав ен:

⁹ 0 = ^arcsin ( ^{n 2}

^{1 ) 12} / ^{n s}

74 ° .

Заметим, что если SIL или NAIL освещать кольцевым световым пучком, то в фокусе возникнет картина дифракции, описываемая не ф ункци ей Эйри (и не sinc -функцией в 2D случае), а ф ункци ей Бесселя нулевого порядка. Поэтому теоретический предел разрешения в среде б удет равен:

Из последнего равенства след ует выражение S _max = ( n ² -1)^1/2. Для кремния и длины волны % = 1550 нм получим S max = 3,32, так как n = 3,47. Тогда минимальный диаметр по полуспаду интенсивности фокусного пятна на выходе планарной ГС-линзы будет равен ( n = 3,47):

FWHM = 0,36 % = 0,104 % .

n

FWHM = 0,44 — =

NA

= 0,44 . %   = 0,44-%- = 0,133 % .

V n — 1        S max

Теоретический предел разрешения (в планарном случае), который можно получить с помощью твёрдотельной иммерсионной оптики ближнего поля: SIL (solid immersion lens) [7], NAIL (numerical aperture increasing lens) [8] – равен ( n = 3,47):

FWHM = 0,44 - = 0,127 % .                (10)

n

Но не все волны, вошедшие в ГС-линзу, выйд ут из неё. Если среда, в которую входят волны от источника, имеет конечные размеры вдоль оптической оси z , то пусть это будет плоскопараллельная пластина толщиной d . Тогда волны, прошедшие эту пластину, на выходе из неё будут описываться выражением:

E ₃ ( x , z ) =

^

= E ₀ j T , ( S ) exp ^- ik S x + ikz^ 1 - S 2 ] d S ,

-M

где

2д/(1 - S 2 )( n ² -S 2 ) cos A - i ( n ² +1 - 2 ^ 2 )sin A

0 <|S| <  1,

T (S = I                                 _____________

² I 27( S 2 - 1)( n ² -S ²) cos A - ( n ² +1 - 2 S 2 )sin A ’

1 <|S| <  n ,

2V( ^ ² - 1)( S 2 - n ²)

2-7( S ² - 1)( S ² - n ²) ch B - ( n ² +1 - 2 S 2 )sh B ’

I^S >  n ,

A = iB = kd ( n ²- S 2 )¹ / ². Величины T ₂( S ), как и T 1 в формуле (7), представляют собой коэффициенты, полученны е по формулам Френеля для трёх различных случаев . Из (13) следует, что распространяющиеся от источника плоские волны (0 < | S | < 1)

пройдут сквозь пластину и опять буд ут распространяться за пластиной под теми же углами (среда перед и после пластины – воздух n = 1). Поверхностные волны первого типа (1 < | S | <  n ) преобразуются в моды внутри плоскопараллельной пластины и в по-

верхностные волны на противоположной (от источника) поверхности пластины. То есть эти волны не будут распространяться в пространстве за пластиной. Поверхностные волны второго типа (| ^ | >  n ) преобразуются в поверхностны е волны на ближайшей (к источнику) стороне пластины , и до противоположной стороны пластины будут «доставать» только их экспоненциально затухающие «хвосты». Поэтому в ГС-линзе центральные лучи от источника, распространяющиеся в ГС-линзе под углами к оптической оси меньшими, чем 0 1 = arcsin ( 1 n ) = 17 ° для n = 3,47, будут проходить через линзу и далее распространяться за линзой. А поверхностные волны первого типа будут распространяться от источника в ГС-линзе, как в кольцевом резонаторе [13], и не буд ут выходить из неё. Поверхностны е волны второго типа буд ут распространяться от источника, как поверхностные волны ГС-линзы , рассеиваясь частично на её острых углах, так как линза не является плоскопараллельной пласти ной и ограничена по поперечным координатам.

Поэто му если считать, что фокусно е пятно в ГС-линзе создаётся только распространяющимися волнами с максимальным наклоном, равным θ 1 , то ширина фокуса должна быть равной ( n = 3,47; 6 1 = 17°) FWHM = 0,44 %/ n sin 0 1 = 0,43 % . А если учесть, что в формирование фокуса вносят существенный вклад поверхностные волны первого типа, которые распространяются в ГС-линзе с максимальным наклоном к оптической оси, равным θ 0 = 74°, то диаметр фокусного пятна должен быть равен FWHM = 0,44 1/ n sin 0 _O = 0,132 % . Эта цифра хорошо согласуется с результатами моделирования [12] и с формулой (9), которая, собственно, приводит к тому же результату, только другим путём.

На рис. 1 показана характерная зависимость ширины фокусного пятна от ширины спектра плоских волн, дающих вклад в этот фокус, согласно формуле (9).

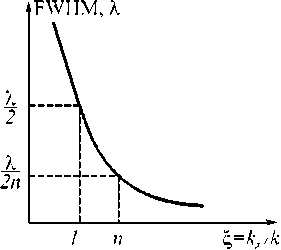
Рис. 1. Зависимость диаметра изображения точечного источника (9) от ширины спектра плоских волн, включая поверхностные исчезающие волны, достигающих плоскости изображения

Таким образом, если моделирование покажет, что диаметр пятна в ГС-линзе меньше дифракционного предела в среде (10), то это означает, что в формировании этого фокусного пятна участвуют поверхностные волны второго типа.

• 4.    Числовые апертуры оптики ближнего поля

Сравним числовые апертуры линз ближнего поля (SIL и NAIL) и ГС-линзы. В разделе 2 кратко это уже было сделано. Пусть в вакууме распространяется сходящийся световой пучок с числовой апертурой NA = sin θ, где θ – максимальный угол, который образуют лучи этого пучка с оптической осью. Если такой пучок войдёт в сред у с показателем преломления n и плоской границей раздела сред, то его числовая апертура не изменится NA = n sin β = sin θ , где β – максимальный угол лучей этого пучка в среде. Для того чтобы увеличить числовую апертуру исходного пучка, используют SIL. Это полусфера из материала с показателем преломления n , расположенная своей сферической поверхностью к падающим лучам таким образом, чтобы лучи падали на эту поверхность нормально (рис. 2 а ). Тогда лучи сходящегося пучка соберутся в фокус в центре полусферы и числовая апертура светового пучка внутри этой полусферы б удет равна NA SIL = n sin θ. Таким образом с помощью оптики ближнего поля (ближнее поле потому, что фокус формируется на плоской поверхности полусферы) можно в n раз ув еличить числовую апертуру исходного светового пучка или в n раз уменьшить диаметр фокусного пятна.

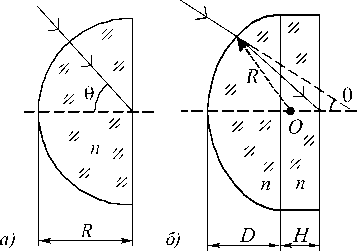
Рис. 2. Схема падения и преломления лучей в SIL (а) и NAIL (б)

Другой тип линзы ближнего поля – NAIL – позволяет ещё более увеличить числовую апертуру пучка. В отличие от SIL на пути лучей сходящегося светового пучка располагается сегмент сферы (меньше полусферы). При этом лучи должны падать на сферическую поверхность таким образом, чтобы их угол с оптической осью был меньше угла, образованного с этой осью нормалью к сферической поверхности, проходящей через точку пересечения луча со сферой. При этом к сегменту сферы следует добавить цилиндр радиусом как у сферы и высотой H, сделанный из того же материала, что и сфера. Цилиндр подбирается таким образом, чтобы лучи фокусировались как раз на пересечении его задней плоскости с оптической осью. Пусть сфера (шар) имеет радиус R, высота сегмента D < R, тогда если высота цилиндра находится из уравнения D + H = R (1 + 1 / n), то фокус сформируется на выходной (для лучей) плоскости цилиндра (рис. 2б). На рис. 2б видно, что луч преломляется в линзе и пересекает оптическую ось под углом большим, чем угол θ у падающего на линзу луча. При этом, если числовая апертура падающего на NAIL светового пучка была равна NA = sin θ, то числовая апертура пучка лучей в цилиндре, сходящихся на выходной плоской по-12

верхности, будет равна NA NALL = ( n - cos 9 ) . Можно показать, что NA _nAll >  NA_SLL . Если сравнить эти числовые апертуры с числовой апертурой ГС-линзы 12

NA = 1 n - 1 ) = n sin 9 0 , то различие будет небольшое: максимальная числовая апертура для рефракционной       оптики       ближнего       поля

NAnAll = NAsll = n = 3,47 отличается от числовой апертуры градиентной линзы NA = 1 n -1) = 3,32

всего на 5%. Однако заметим, что линзы SIL и NAIL только собирают свет от источника и преобразуют поверхностные волны первого типа в распространяющиеся волны, но не фокусируют собранный свет. Для последующей фокусировки требуется дополнительная рефракционная оптика. В отличие от этого ГС-линза и собирает свет от источника, и фокусирует его на своей выходной поверхности.

• 5.    Уменьшение фокусного пятна с помощью модуляции показателя преломления

В недавних работах [15,16] показано численно, что с помощью субволновых дифракционных решёток можно поверхностные волны от источника преобразовать в распространяющиеся волны и достичь сверхразрешения λ / 20. В [15] для этого использовались неограниченные по апертуре, уложенны е друг на друга несколько дифракционных решёток с разным субволновым периодом, а в [16] использовалась металлическая субволновая дифракционная решётка с очень большой диэлектрической проницаемостью (ε = –100). Однако в этих работах не использовался оптический элемент для фокусировки света.

Моделирование с помощью программы FullWAVE, реализующей FDTD-метод, показало, что добавление к градиентной ГС-линзе субволновой дифракционной решётки или выполнение ГС-линзы в бинарном виде с субволновыми неоднородностями приводит к уменьшению ширины фокусного пятна на 10% и 20%.

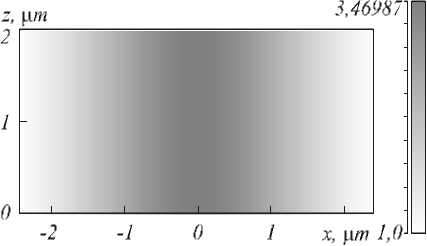
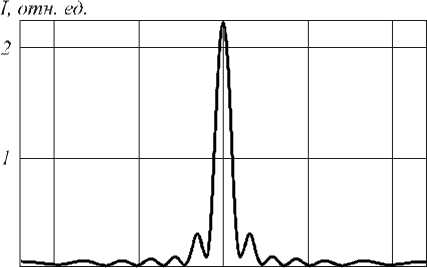
На рис. 3 по казан в серых то нах профиль пока-зат еля преломления ГС-линзы ( а ) и распределение интенсивности на выходе из линзы ( б ). Ширина фокусного пятна на рис. 3 б равна

FWHM = 191 нм = 0,123λ,

λ = 1,55 мкм. Это значение немного меньше дифракционного предела в кремнии (10), что доказывает, что в формировании фокусного пятна в ГС-линзе участвуют поверхностные волны второго типа.

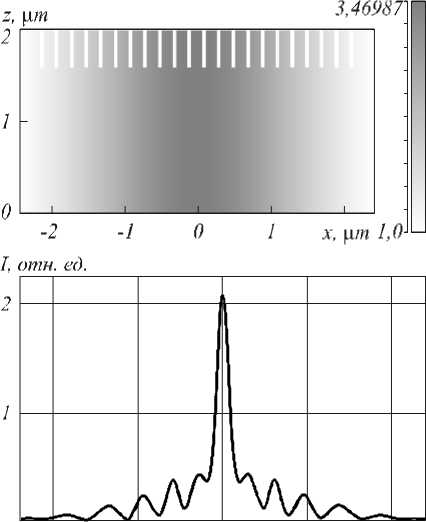
На рис. 4 показана та же ГС-линза, что и на рис. 3, но в верхней её части (на выходе) имеется субволновая дифракционная решётка ( а ), а на рис. 4 б показано распределение интенсивности на выходе из этой линзы. Ширина фокусного пятна на рис. 4 б равна FWHM = 177 нм = 0,114λ. Это на 8 % меньше, чем ширина фокуса на рис. 3 б , и на 10% меньше дифракционного предела (10).

б)

Рис. 3. Распределение показателя преломления в градиентной ГС-линзе (а) (на оси показатель преломления 3,47), горизонтальный размер – 4,8 мкм, вертикальный – 2 мкм. Свет распространяется вертикально. И поперечное распределение интенсивности |E|2 на выходе из линзы (на расстоянии 10 нм от неё) (б)

Рассмотрим двумерную зонную линзу, размеры зон которой подобраны таким образом, что эффективный показатель преломления описывается формулой (7). Такую зонную линзу б удем называть бинарной ГС-линзой.

На рис. 5 показан профиль градиентной и бинарной ГС-линз. Радиус линзы разбит на отрезки [ x m , x m +1 ], m = 0, 1, 2, ..., M , в каждом из которых подобрана точка x m <  x m^b <  x m +1 такая, что на отрезке [ x m , x m^b ] материал линзы – кремний , а на отрезк е [ x m^b , x m +1 ] – воздух. Точка x m^b выбирается так, чтобы аппроксимировать показатель преломления (8):

x m + 1

J ⁿ ( x ) = ⁿ 0 ( x m ^- x m ) ⁺ ( x m + 1 ^- x mm ) .             ⁽¹⁴⁾

xm

На рис. 6 а показана бинарная ГС-линза, полученная по формуле (14) для линзы на рис. 3 а , а на рис. 6 б – распределение интенсивности в фокусе на выходе из этой линзы. Ширина фокусного пятна на рис. 6 б равна FWHM = 159 нм = 0,102λ. Это на 17 % меньше, чем ширина фокуса на рис. 3 б и на 20% меньше дифракционного предела (10). То есть в формирование фокусного пятна (рис. 6 б ) на выходе бинарной ГС-линзы, согласно графику на рис. 1, на 20% вносят вклад поверхностные волны второго типа ( k x >  nk ).

В работе получены след ующие результаты:

– в интегральном представлении амплитуды ТЕ-вол-ны светового поля от точечного источника в 2D среде и за плоскопараллельной пластиной выделены три слагаемых, описывающих три типа световых волн: распространяющиеся волны и поверхностные (неоднородные затухающие) волны первого и второго типов;

• б)      -2        -1 О 1 R, мкм

Рис. 4. Распределение показателя преломления в градиентной ГС-линзе (а) (на оси показатель преломления 3,47), горизонтальный размер – 4,8 мкм, вертикальный – 2 мкм. В верхней части ГС-линзы имеется дифракционная решётка глубиной 0,4 мкм с периодом 0,2 мкм и шириной канавок 0,05 мкм (внутри канавок – воздух). Свет распространяется снизу вверх.

И поперечное распределение интенсивности |E|2 на выходе из линзы (на расстоянии 10 нм от неё) (б)

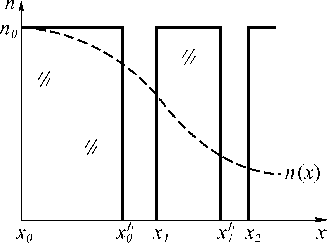
Рис. 5. Профили показателя преломления градиентной (пунктирная линия) и бинарной (сплошная линия) ГС-линз.

Заштрихованные области – кремний

– произведено сравнение числовых апертур рефракционных линз ближнего поля (SIL, NAIL) и план арной гиперболической секансной линзы и показано, что они близки между собой и отличаются для кремния всего на 5%;

– моделированием с помощью программы FullWAVE показано, что добавление к градиентной гиперболической секансой линзе субволновой дифракционной решётки или замена такой линзы её бинарным аналогом приводят к уменьшению ширины фокусного пятна на 10% и 20% по сравнению с дифракционным пределом в данной среде; это означает, что в формирование субволнового фокусного пятна на выходе ГС-линзы на 10% и 20% дают вклад поверхностные волны второго типа.

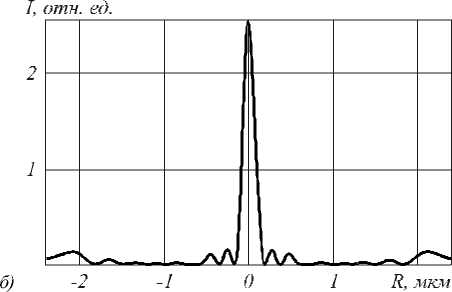
Рис. 6. Бинарная ГС-линза (а) (показатель преломления 3,47), горизонтальный размер – 4,8 мкм, вертикальный – 2 мкм, минимальная канавка – 20 нм (внутри канавок – воздух). Свет распространяется вертикально.

И поперечное распределение интенсивности |E|2

на выходе из линзы (на расстоянии 10 нм от неё) (б)

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9) и молодого кандидата наук (МК-64571.2010.2).