Механизм тепломассообменного процесса в динамической теплоизоляции кондиционируемой одежды

(тепловой поток с интенсивностью q 1 ) и тепло, поступающее через оболочку 2 (тепловой поток с интенсивностью q 2 ). Количество снимаемого тепла определяется расходом кондиционирующего воздуха и возможностью его подогрева.

Q 2 – Q 1 = G П С р ( T 2 – T 1 ) (1)

Как правило, такая схема термостатирования принципиально не экономична из-за существования допустимой степени подогрева воздуха T 2 – T 1 , определяемой максимальной температурой объекта T 2 и располагаемой температурой охлаждающего воздуха T 1 или минимальной допустимой температуры объекта. Увеличение экономичности схемы термостатирования, на наш взгляд, возможно путем изменения направлений взаимодействия тепловых потоков и направления движения воздуха. В проточной схеме «а» внешний тепловой поток интенсивности q 2 перпендикулярен потоку движения воздуха с расходом G П . В предлагаемой динамической схеме «б» направление движения воздуха организовано навстречу тепловому потоку. Для этого воздух, после снятия тепла с поверхности термостатируемого объекта (тепловой поток интенсивности q 1 ), меняет направление на 90^o и удаляется наружу через волокнистую термоизолирующую оболочку 3, т.е. движется навстречу внешнему тепловому потоку.

Количество снятого тепла

Q 2 – Q 1 = G d C p ( T 2 – T 1 ) +

+ G d C p ( T 4 – T 2 )

G ≥ ^{q 1}

^d C p ( T 2 - T 1 )

Сравним (1) и (2).

G П C p ( T 2 – T 1 ) = G d C p ( T 2 – T 1 ) +

+ G d C p ( T 4 – T 2 )

В конечном виде

G П ₌ T 4

G d   T 2

-

-

^{T 1} = 1 + ^{T 4}

T 1       T 2

-

-

T 2

T 1

при условии обеспечения q 1 ≤ G d C p ( T 2

-

T 1 )

,

т.е. расход воздуха должен быть достаточным для снятия тепла выделяемого термостатируемым объектом и поддержания его температуры в заданных пределах. Из соотношения видно, что возможности снятия тепла с использованием динамической изоляции за счет полного использования теплоаккумулирующей способности воздуха потенциально выше, чем при просто прокачке охлаждающего воздуха через зазор. В уравнениях (1)-(4) мы оценивали только потенциальную возможность снятия тепла охлаждающим воздухом без связи с тепловым потоком извне q 2 .

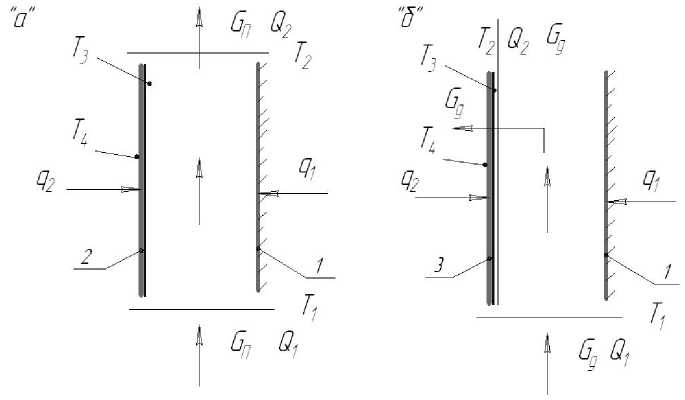
Рис. 1. Расчетная схема термостатирования: «а» - проточная, «б» - динамическая

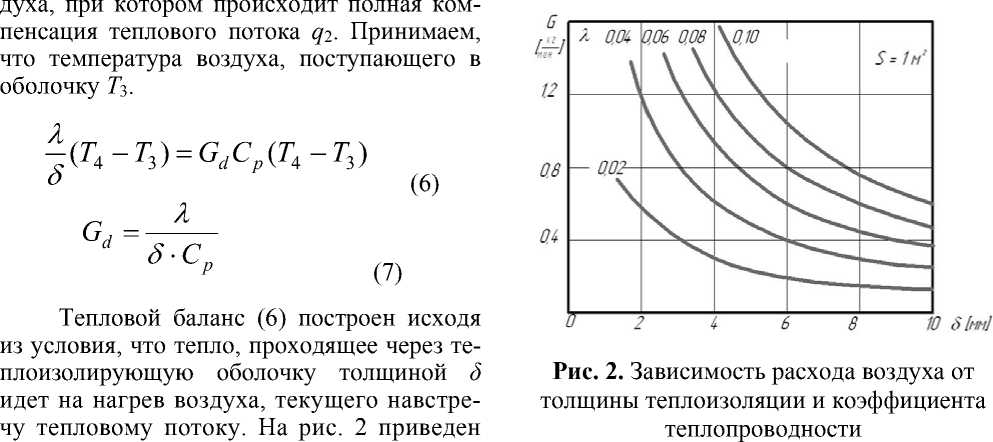
расход воздуха в зависимости от толщины теплоизоляции δ и коэффициента теплопроводности λ .

Рассмотрим тепловой баланс в единицу времени через единицу площади оболочки и определим расход охлаждающего воз-

Полученные значения расхода охлаждающего воздуха (7) являются предельными и, они достижимы только при условии обеспечения некоторых теплообменных процессов. Рассмотрим механизм теплообменных процессов, протекающих в динамической теплоизоляции. Пористый материал состоит из твердых волокон, пространство между которыми заполнено воздухом. Рассмотрим гипотетический перенос тепла через тонкую пространственную конструкцию, осуществляемый теплопроводностью. Теплообмен через волокна и воздух представим как два отдельных независимых процесса. На рис. 3 приведена условная расчетная схема структуры волокнистой теплоизоляции, состоящей из цилиндрических элементов, окруженных воздухом.

^ S TT. - T , ) = ^Л S м ,_t (T . - Т з ) +

%          ^l            (9)

+ Л ( S - S м ) -t ( T _a - Т з )

О

Масса теплоизоляции

S • S •p- SMlpM . (io)

Решаем совместно уравнения (9) и (10) и определяем отношение эквивалентной длины волокон l к толщине § .

Г Л ² х Р I О ^Лм    I

Рм V 1 )

Л ^р 1 О 1

Рм V 1 )

- Л - Л = 0

в

О l

Л . Р

² Р м

г

', Р

V ^{2 Р} м у

+ Л - Лв

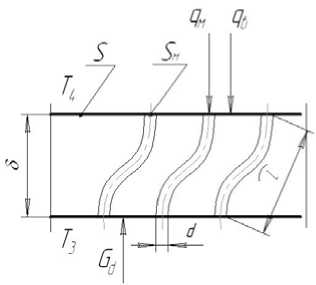
Рис. 3. Условная расчетная схема структуры волокнистой теплоизоляции:

q_м, q_B — тепловые потоки, проходящие через твердые элементы и окружающий воздух соответственно, q_м + q_e = q ₂; S - площадь поверхности динамической изоляции; S_M - суммарная площадь сечения твердых конструктивных элементов; L - эквивалентная длина волокон теплоизоляции; X , Х м , Х в , - коэффициенты теплопроводности динамической изоляции коэффициенты теплопроводности материала твердых элементов, коэффициент теплопроводности воздуха соответственно; р, р м - плотность динамической изоляции и плотность материала твердых конструктивных элементов соответственно; Т ₃, Т 4 -температура внутренней и наружной поверхностей динамической изоляции соответственно.

Тепло, передаваемое через теплоизоляцию, рассмотрим состоящим из тепла, передаваемого через конструкционный материал Q_м и передаваемое через заполняющий ее объем воздуха Q_e .

Q = Q m + Q e (8)

По статистической оценке для большинства тканевых теплоизолирующих материалов X / 1 <0,2, т.е. средняя эквивалентная длина теплопроводящего элемента значительно превышает конструктивную толщину ткани. Исходя из этого, соотношение площади поверхности теплопроводящего элемента к площади теплопроводящего сечения, например для ткани толщиной 4 мм и диаметром нити 0,1 мм.

nd±8 = %_ = 200 0,2 • п • d2   0,20

Этого вполне достаточно для снятия через боковую поверхность тепла, передаваемого по нити ткани. Схема механизм теплопередачи внутри ткани через воздух приведена на рис. 4. Выделим слой воздуха толщиной d§ , движущейся навстречу тепловому потоку. Считаем, что тепловой поток за время dT повышает температуру воздуха на dT . При условии блокирования теплового потока минимальная скорость перемещения воздуха должна обеспечить за dT перемещения нагретого слоя на d§ .

"^S • dT • dT = SV • d • трСndT dS                  Рб p

(14),

где V - скорость движения воздуха.

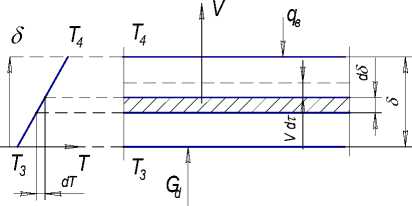
Рис. 4. Схема тепломассообмена через воздух внутри ткани

После интегрирования получаем

V ■ min

λ в δρ С p

Ст,

G d min

λ δ C p

(16), что по структуре соответствует ранее выведенной формуле (7). При определении минимального расхода воздуха, достаточного для блокирования поступающего извне тепла, правомерно использование справочных значений коэффициента теплопроводности рассчитываемой волокнистой теплоизоляции.

Выводы:

• 1.    Изменение направления движения охлаждающего воздуха приводит к более рациональному использованию его теплоаккумулирующих возможностей и значительно сокращает потребный расход.

• 2.    Минимальное потребное количество охлаждающего воздуха, достаточного для полного блокирования внешнего теплопри-тока в динамической теплоизоляции, не зависит от перепада температуры на внешней и внутренней поверхностях оболочки.

• 3.    Существует целесообразная предельная величина толщины динамической теплоизоляции, зависящая от теплопроводности.