Механизм управления процессом сходимости итерационного метода Ньютона
Автор: Никонов Эдуард Германович, Казаков Дмитрий Сергеевич
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 1, 2017 года.
Бесплатный доступ
В работе приведен краткий обзор итерационных численных схем, основанных на методе Ньютона. Проведено сравнение различных численных методов ньютоновского типа. Исследовано влияние итерационного параметра в непрерывном аналоге метода Ньютона на область и скорость сходимости. Предложен подход к оптимизации процесса сходимости непрерывного аналога метода Ньютона (НАМН). На основании данного подхода разработан механизм управления скоростью сходимости непрерывного аналога метода Ньютона с использованием в качестве управляющего параметра - коэффициента изменения шага разностной схемы для численного решения дифференциального уравнения НАМН. На основе разработанного механизма управления процессом сходимости была предложена модификация непрерывного аналога метода Ньютона.
Итерационные методы, скорость сходимости, нелинейные уравнения, непрерывный аналог метода ньютона
Короткий адрес: https://sciup.org/14122647
IDR: 14122647
Текст научной статьи Механизм управления процессом сходимости итерационного метода Ньютона
При решении широкого круга вычислительных задач в различных областях науки и техники возникает потребность численного решения уравнений одного или нескольких переменных, в частности при использовании неявных разностных схем для решения обыкновенных дифференциальных уравнений и уравнений в частных производных, интегральных и других, как правило, нелинейных уравнений. Использование традиционных итерационных методов часто является малоэффективным из-за довольно большого количества итераций, что неминуемо приводит к значительному увеличению времени вычислений. Вопрос о построении эффективных алгоритмов решения нелинейных уравнений остается актуальным в вычислительной математике и ее приложениях, в частности математическом моделировании, например, при моделировании методом молекулярной динамики, где на каждом временном шаге необходимо решать от 103 до 107-1010 дифференциальных уравнений. В этом случае цена даже одной итерации при решении одного уравнения возрастает в миллионы раз [1]. Одним из эффективных итерационных методов решения нелинейных уравнений является метод Ньютона и различные его модификации в том числе на основе НАМН.
В данной работе проанализированы итерационные численные схемы, основанные на методе Ньютона. Проведено сравнение различных численных методов ньютоновского типа. Исследовано влияние итерационного параметра в непрерывном аналоге метода Ньютона на область и скорость сходимости. Предложен подход к оптимизации процесса сходимости непрерывного аналога метода Ньютона (НАМН). На основании данного подхода разработан механизм управления скоростью сходимости непрерывного аналога метода Ньютона с использованием в качестве управляющего параметра коэффициента изменения шага разностной схемы для численного решения дифференциального уравнения НАМН. На основе разработанного механизма управления процессом сходимости была предложена модификация непрерывного аналога метода Ньютона.
Метод Ньютона и его роль в решении нелинейных уравнений
Вывод формулы метода Ньютона основан на формуле уравнения касательной [2], проведённой к графику функции f(x ) в точке х* достаточно близкой к решению уравнения f(x ) = 0
Лx) = №) + f'(x)(x - Xo).(1)
Предполагая, что решение х * уравнения /( x )=0 лежит в окрестности точки х 0 и f'(x 0 )+0, подставляя x = х * в формулу (1),
0 « №) + Г(хо)х* - f'(xo) Xo получим следующее приближённое выражение для неизвестного решения х*
X* ~ Xo - /(Xo)/'(Xo)
Этот алгоритм позволит получить новое приближение х 1 к решению уравнения х * , если производная существует и не равна нулю на всём участке (х * ; х 0 )
х1 = хо - /(хо)/'(хо)-1.
Теперь это новое приближение х 1 можно использовать вместо старого х 0 для того чтобы найти ещё более точное приближение х 2 к решению уравнения х * . Если известно значение х^ на i -ом шаге итерационного процесса, то следующее приближение можно получить по формуле:
X i = X i-1 - f(X i- 1)f(X i- 1) 1
Формула (5) определена для всех i = 0,1,2,3^ если функция f(x ) имеет производную не равную нулю на всём участке ( x0; X * ).
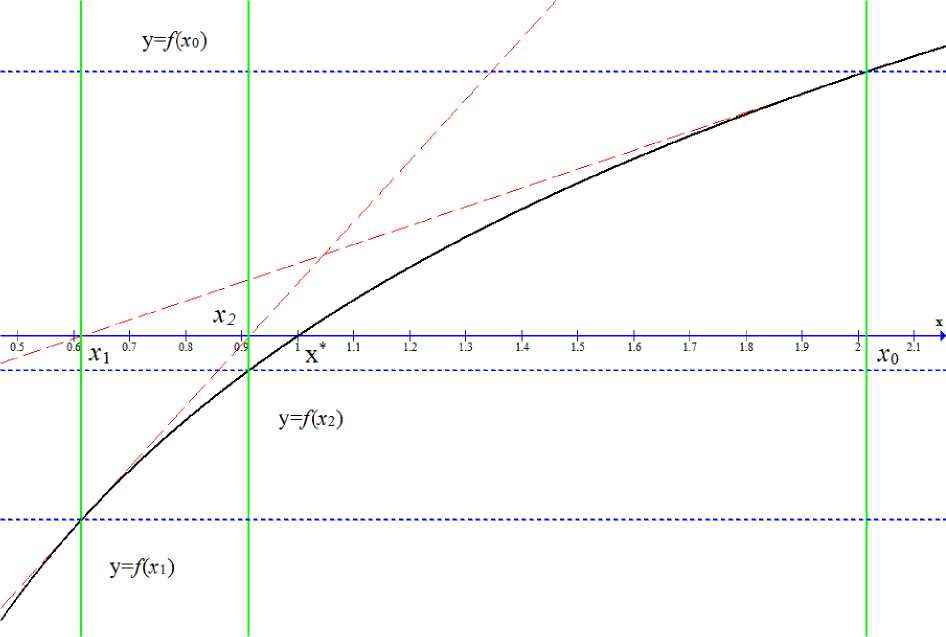
Рис. 1. Пример применения метода Ньютона для решения нелинейных уравнений
Непрерывный аналог метода Ньютона
В методе Ньютона (5) вычисляемое на каждом шаге значение X i можно рассматривать как функцию целой переменной i : X i = x(i), причём x (0) = X 0 задано.
Возможно рассмотреть целую переменную i как непрерывную переменную t , 0 < t < да, и предполагая что функция x(t) дифференцируема, мы вместо формулы (5) получаем следующее выражение:
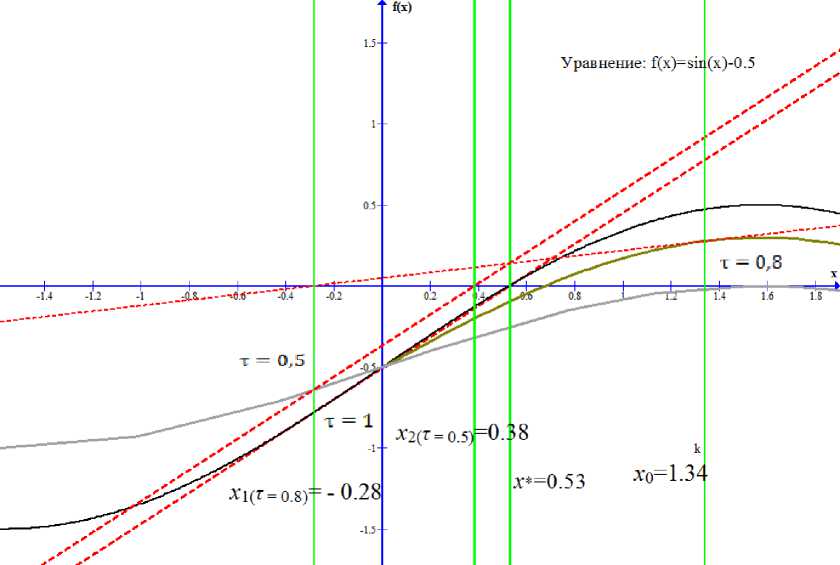
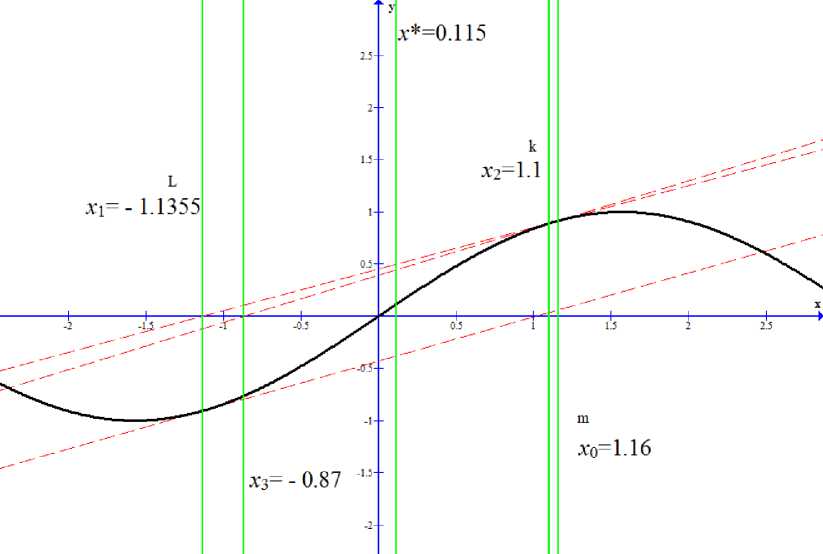
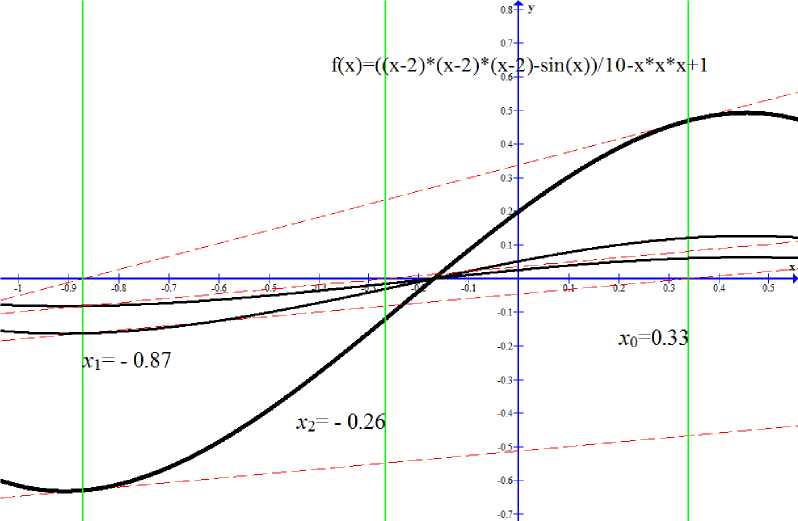
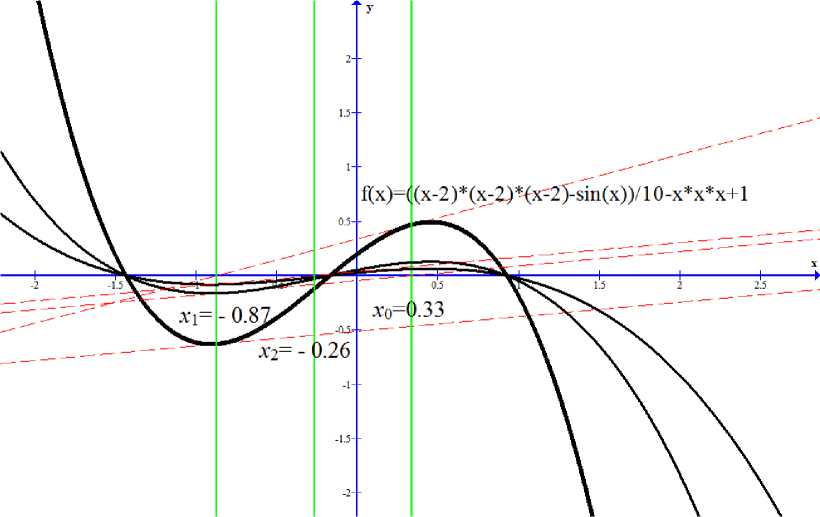
x'(t) = -/(x(t))/'(x(t))-1, 0 Уравнение (6) обычно можно решить только приближённо. Можно использовать для его решения метод Эйлера[3], один из простейших методов приближённого решения задачи основанный на приближённом представлении производной x‘(t) в фиксированной точке t в виде: X (t) x(t + At) — x(t) At' где At - малое приращение аргумента t. Зададим систему точек: t = ti, i = 0,1,2,3_, Tt = ti+i- ti, to =0, t > 0; где t - расстояние между соседними точками. Мы можем, используя (7), получить в каждой точке приближённое соотношение для уравнения (6) X(ti+1)-X(ti) Tt ~ -f(x(ti■ х t x(tо) = х0, i=0,1,2,3 .... Переход к точному равенству свяжет между приближёнными значениями х^= x(ti) решения х(t) в соседних узлах, в результате мы получим следующую формулу: Xi = Xi-1 -Ti-if(xi-i)f'(xi-i) 1, i = 0,1,2,3... . Коэффициент размера шага должен удовлетворять условию 0 < т< 1. Преимущества НАМН перед другими методами Важным достоинством метода Ньютона является квадратичная сходимость вблизи искомого корня х*. Однако если f"(x) меняет на отрезке хп<x< хп+1 свой знак, метод Ньютона может не привести к решению х*, то есть последовательность хл может быть расходящейся. Предельным случаем расходимости последовательности можно считать «зацикливание», которое выражается отношениями: х1 = хо - f'(Xo)-1 f(xо), (9) х2 = хо = х1 - f'(X1)-1f(X1). Такое «зацикливание» можно наблюдать, например, для функций f(x), у которых решение х* является в некоторой своей окрестности точкой центральной симметрии, то есть выполняется условие: f (х) = — f(2xi - х). Ясно, что если найдётся такое х0, для которого х1 = 2х^ - х0(х^ неизвестно), то в силу последнего условия произойдёт «зацикливание» х2= х0. По сравнению с методом Ньютона его непрерывный аналог позволяет установить существование решения х* нелинейного уравнения и сходимость к нему при t ^ да своего решения х(t) от начального условия х(0) = х0, при менее ограниченных условиях, налагаемых на функцию f(x). Введение параметра τ позволяет увеличить область сходимости метода и, соответственно, не допустить зацикливания. Рис. 2. Пример преимущества НАМН перед Методом Ньютона Для решения уравнения f (x) = sin(x) (рис. 2), применяется метод Ньютона, НАМН при т = 0,7 и т = 0,5. Начальное приближение выбрано на монотонном участке функции, содержащем корень: х0 = 1.2. В результате одной итерации выполненной для каждого из перечисленных выше методов получены значения для х1. Для метода Ньютона это будет х1 = -1.4, несмотря на то что значение по прежнему принадлежит монотонному участку функции, содержащему корень, очевидно, что результат некорректен и метод расходится, в качестве подтверждения этой гипотезы мы можем посчитать х2 = 4.4. Посчитанный для НАМН при т = 0,7: х1 = -0,6. Несмотря на уменьшенный размер шага, очевидно, что следующие итерации сходятся к решению уравнения. Значение, полученное для НАМН при т = 1 ещё ближе к корню х1 = -0,082. Из этого можно сделать вывод что несмотря на меньшую скорость сходимости, НАМН обеспечивает более устойчивую сходимость чем метод Ньютона, а удачно подобранное значение управляющего параметра т может значительно уменьшить количество итераций. Способ задания управляющего параметра для НАМН В статье [4] доказано что, использование формулы (8) уменьшит значение Ньютоновской поправки и и, вследствие этого, увеличивается область сходимости метода. Так как необходимо сделать большее количество шагов по методу Эйлера, то это приведёт к уменьшению скорости сходимости. Естественно возникает задача: научится управлять размером коэффициента т таким образом, чтобы он обеспечивал максимальную скорость сходимости на каждом шаге итерационного процесса. При т; = 1 итерационный процесс (8) совпадает с классическим методом Ньютона. В работе [4] доказана сходимость итераций: f(Xt) U; = — /(х;), х1+1 = X; + т;П;, i = 0,1,^, 0 < т; < 1 О0) к решению эволюционной задачи: ^/(x (t)) = - /(x(t)), x(0) = хо, на конечном отрезке 0 В практических расчетах итерационный процесс (8) дополняется алгоритмами задания шага т, от удачного выбора которого может зависеть как сходимость метода, так и скорость сходимости. В настоящее время существует несколько алгоритмов задания шага т. Пусть в некоторой сфере D с центром в точке х0существуют производные /'(х), /"(х) причем линейный оператор /'(х) - обратимый и имеют место неравенства: I /'(х)-1! < B, «/"(х) I < M.(11) Предположим, что все приближения х;, полученные с помощью итераций (10), принадлежат сфере D. Тогда легко показать [2], что: / (х;+1) — ^;+1(т;)« /(х;)1, i = 0,1,^, где коэффициент перехода ^;+1(т;) от итерации к итерации определяется по формуле: ^;+1(т) = 1 - т + yMB2ll /(х;)1, 0 < т < 1. Выберем т; так, чтобы выполнялось условие: ^;+1(т;) = min ^+1(т), 0 < т < 1. Такой шаг т; назовем оптимальным и итерационный процесс (10) с оптимальным шагом т; назовем оптимальным по скорости сходимости. Точка минимума функции (13) tt* = Cмв2N7Cx^)N)"1= (e)-1. (14) Пусть Et< 1. Тогда tt* > 1, т. е. в этом случае tt = 1 и поэтому ^t+i(tt) = ^;+1(1) < i. Если же s > 1, то tt* < 1 и, следовательно, i^ t+i(t t*) = 1 - i^ > |. Однако если в оценках (11) конкретные значении констант В и М неизвестны, то найти точку минимума tt* невозможно. Вместо оптимального шага tt необходимо найти другой шаг, позволяющий уменьшать невязку от итерации к итерации. Заметим, что для функции (13) выполняется условие: ^' t+i(0) = М0) = - 1.(15) Потребуем, чтобы дискретные аналоги производных ^'t+1(0) и 1^/(0) тоже удовлетворяли соотношению (1.9), т. е. [^t+i(ti) - ^t+i(0)l/tt = [ ^t (tt-i)- ^t(0)] / tt-i Подставляя (13) в соотношение (16), получаем (8): -2- = 12^=121. < = 12 (17) гн IIZCX£)H Исследования коэффициента размера шага для НАМН В процессе расчётов по методу (8), стоит подробно рассмотреть момент, когда /(а) меняет свой знак на отрезке [%t-i;%t]• В силу нашего предположения, что /(%) имеет единственный корень %* на отрезке [%t-i;%t]и //(%)#0, очевидно, что, значение %t-iдолжно быть больше значения %t+i, в этом случае нет необходимости в расчёте коэффициента tt+i, при помощи алгоритма (8) так как нам известно значение %t-i, которое можно использовать для расчёта коэффициента tt+i. Зададим коэффициент к, обозначающий такое %t-i, при котором ^у- 1- < 0. Используя формулу (8) мы можем вычис- лить значение tt+i, необходимое для того чтобы %t+i= к V = f^t-iWt-a i; (к -%t-i) tt+i = v ■ Если вычисленное значение t > 1, тогда мы задаём t = 1 и используем алгоритм (8) для расчёта %t, сохраняя при этом квадратичную скорость сходимости. Наиболее интересен случай, когда t < 1, очевидно что необходимо уменьшить значение шага. На основании данных полученных в ходе ряда тестовых расчётов, было принято решение использовать следующий алгоритм: <Р(к) , п _ фО^) - _ - Значение t находим при помощи алгоритма (18), коэффициенты m и l значения по оси абсцисс, полученные в процессе решения, предшествующие каждый со своей стороны k и %t соответственно. На участке, где функция меняет свой знак, возможна крайне низкая скорость сходимости НАМН, подобный случай описан в [3], было принято решение, при условиях: l|t||-||m|| ||Z-xnH+Hm-kH > 5; i > 4; i = 1,2,3,.... Где i - количество итераций подряд сделанных в условиях двухсторонней сходимости. Использовать алгоритм для определённого шага %t+i: %t + 2 = H^iN - N^N ■ Следующий шаг считается, уже используя алгоритм (18). Очевидно, что алгоритм (21) увеличивает скорость сходимости по сравнению с тем что даёт метод Ньютона в подобной ситуации, так же исключает зацикливание (9), увеличивая область сходимости. На рисунках 3-4 применяется модифицированный алгоритм НАМН для решения уравнения f(x) = sin(x) - 0.5 и f(x) = sin(x) соответственно, значение полученное при помощи этого метода сравниваются со значениями, полученными при помощи обычного НАМН. Рис. 3. Преимущества модифицированного НАМН Рис. 4. Модифицированный НАМН для случая с зацикливанием Рис. 5. Пример применения модифицированного НАМН для решения нелинейных уравнений Рис. 6. Пример применения модифицированного НАМН для решения нелинейных уравнений Заключение На примере разработанного алгоритма для модифицированного НАМН, было показано, что возможно управлять скоростью сходимости НАМН, используя коэффициент изменения шага разностной схемы для численного решения дифференциального уравнения НАМН, как управляющий параметр. Дальнейшее развитие предполагает использование методов интерполяции для рассмотрения случаев, не предусмотренных модификацией НАМН. Разработка и внедрение механизмов управления итерационными процессами решения уравнений позволит значительно снизить время необходимое на расчёт искомого значения, что значительно повысит эффективность алгоритмов решения нелинейных уравнений.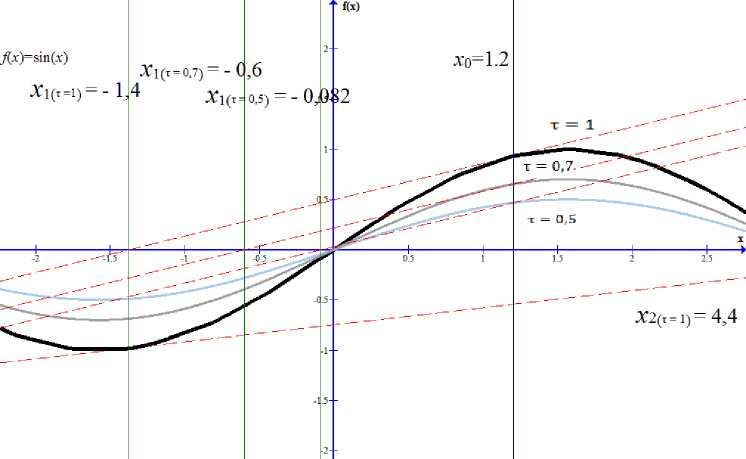
Список литературы Механизм управления процессом сходимости итерационного метода Ньютона
- Nikonov E.G. One class of conservative difference schemes for solving molecular dynamics equations of motion. arXiv:1605.05714v1 [math.NA].
- Алгебра и начала анализа. под редакцией А.Н. Колмогорова. - М.: «Просвещение», 1993.
- Калиткин Н. Н. Численные методы. - М.: Наука, 1978.
- Жанлав Т., Пузынин И. В. О сходимости итераций на основе непрерывного аналога метода Ньютона. - ЖВМиМФ, 1992. - Tом 32. - № 6. - С. 846-856.
- EDN: ZYVLMB


