Механизм жесткости и прочности кости в норме и при старении организма. Наноуровневая модель

Старение организма сопровождается развитием остеопороза – «безмолвной болезни», протекающей асимптоматично до момента нарушения целостности костей [29]. Только в США по этой причине ежегодно происходит 700000 переломов позвоночника,1 по 250000 – шейки бедра и дистального отдела лучевой кости и 300000 – в других частях скелета. Здравоохранению США стоимость лечения последствий остеопороза обходится в 10 млрд. долларов (без учета стоимости длительного ухода на дому).2 В мире количество больных с переломами шейки бедра постоянно увеличивается и согласно расчетам возрастет с 1,7

млн. в 1990 г. до 6,3 млн. в 2050 г. При этом около 20 % пострадавших умирают в течение первого года [12]. Вышеизложенное свидетельствует о том, что остеопороз является социальноэкономической проблемой высокой значимости.

Одним из элементов, обеспечивающих решение этой проблемы, является понимание первичных механизмов изменения механических характеристик внеклеточного матрикса при старении. Именно эти изменения приводят к последующим сдвигам архитектуры на более высоком уровне структурной организации скелета и к потере костной массы [3, 4]. До настоящего времени основной и господствующей моделью, объясняющей механизм обеспечения жесткости и прочности костной ткани, является гипотеза J.D. Currey, разработанная в отделе зоологии Оксфордского университета [23 ].

Концепция J.D. Currey. По мнению этого ав- тора, кость представляет собой двухфазный материал, аналогичный фиберглассу, где смола – аналог коллагена, а стекловолокно – апатита. J.D. Currey подчеркивает, что двухфазные материалы могут функционировать эффективно при наличии устойчивой связи между волокнами и окружающим их веществом, добавляя при этом, что на момент создания модели характер связей между коллагеном и апатитом не ясен. Важным, с нашей точки зрения, является утверждение о том, что любая теория требует очень сильных связей между этими двумя компонентами, иначе модуль упругости кости не будет сколь либо существенно отличаться от его значений у фибрилл коллагена.

В последние десятилетия детализированы не только характер и пространственная организация связей между органическими и минеральными структурами, но и особенности их иерархической организации [1, 2, 7]. Эти данные, с одной стороны, позволяют говорить о несоответствии модели J.D. Currey сегодняшним представлениям, а с другой - разработать теорию, определяющую на современной основе механические свойства костной ткани в норме и при старении организма.

Цель : предложить общую концепцию базисной наноуровневой модели механизма, определяющего, с одной стороны, жесткость и прочность кости на макроуровне, а с другой - увеличение хрупкости внеклеточного матрикса при старении.

Теоретико-экспериментальная основа физико-механической модели. Выполнение поставленной цели (создание модели) регламентируется следующими условиями:

• 1)    отношение модуля упругости E_кт костной ткани к модулю упругости E_ап гидроксиапатита должно соответствовать экспериментальным данным, представленным в литературе;

• 2)    механизм, определяющий жёсткость кости, должен одновременно являться элементом механизма локального повреждения костных структур на наноуровне для случая, когда действующая сила превышает уровень допустимых физиологических нагрузок;

• 3)    механизм, определяющий прочность костной ткани в норме, должен обеспечивать увеличение ее хрупкости при старении.

Результаты исследования модуля упругости . Для костной ткани, образующей компактное вещество у человека, модуль упругости E кт колеблется, по разным данным, в пределах 4-20 ГПа (в среднем 14 ГПа ) [24] или 10-22 ГПа (в среднем 16 ГПа ) [26], что практически одно и то же. У гидроксиапатита этот показатель значительно выше: от 40 до 90 ГПа (в среднем 65 ГПа ) [26] или 114,2 ГПа [16], а у «зелёно-синего» апатита от 54 до 62 ГПа [14]. Таким образом, приведенные значения модулей упругости для каждого объекта являются величинами одного порядка и их отношение, если ориентироваться на данные A.C. Lawson и J.T. Czernuszka [26], составляет:

Е_кт/Е_ап = 0,18-0,30 (в среднем 0,24). При старении это отношение меняется, так как происходит снижение модуля упругости Е кт от его уровня 15,2 ГПa в 35 лет на 2,3 % за каждое последующее десятилетие [32 ] . Путем простых расчетов получаем, что к 75 годам отношение Е кт /Е ап составит 0,16-0,27 (в среднем 0,215).

Модуль упругости коллагена E кол колеблется от 0,01 до 0,57 ГПа [26], то есть на два порядка ниже E_ап. Это позволяет утверждать, что при одинаковых деформациях минерального и органического компонента в последнем напряжения составляют 1 % (и менее) от уровня в минеральном матриксе. Следовательно, коллаген даже теоретически не может обеспечить наблюдаемую жёсткость кости (не только в условиях сжатия, но и в условиях растяжения), которая определяется лишь минеральным компонентом с учетом особенностей структуры его иерархической организации.

Для дальнейших рассуждений выделим следующие основополагающие для разработки модели факты.

• 1.    Кристаллиты гидроксиапатита имеют крайне малый размер, и их величины близки не только у разных организмов, но и при формировании in vitro: ширина – от 7,0 до 15,8 нм , длина – от 13,0 до 37,3 нм и толщина – от 1,5 до 4,0 нм [1, 2].

• 2.    Кристаллиты соединяются между собой конец в конец или бок в бок, формируя копла-нарные структуры. При этом крайне важен тот факт, что полного слияния кристаллических решеток расположенных рядом кристаллитов не происходит. Между ними имеется водная пленка (гидратный слой) [1, 6, 11].

• 3.    Гидратный слой жестко сцеплен с кристаллитами и представляет собой ультратонкий нанослой адсорбата на поверхности адсорбента, что обеспечивает весьма высокий уровень межмолекулярного взаимного притяжения [11, 18].

• 4.    В результате межмолекулярного притяжения водная плёнка связывает кристаллиты между собой.

• 5.    Все структуры начиная с надмолекулярного уровня и до уровня остеонов имеют иерархически построенную винтовую (спиральную) организацию [1, 6, 22], в соответствии с которой выстраиваются и элементы минерального матрикса.

• 6.    При старении минерализация внеклеточного матрикса увеличивается на 12 % и более [19] за счет вытеснения водной [28, 30, 31] и органической [30, 31] составляющих. Доля остеонов, минерализованных на 75 % и выше, достигает 40 % и более от их общего числа, в то время как в молодом возрасте не превышает 10 %. Повышается также удельный вес центральных каналов и остеоцитарных лакун, заполненных минерализованной тканью [25].

• 7.    Размеры копланарных объединений кристаллитов увеличиваются с возрастом (длина на

• 8.    В старших возрастных группах происходит увеличение содержания ионов карбоната (СО₃^--), замещающих в кристаллической решетке ионы фосфата (НРО₄"), а также повышается количество фторидов и таких микроэлементов, как стронций, кремний и медь [9, 19].

• 9.    Возникающие при старении замены в кристаллической решетке возможны только при условии возникновения аналогичных изменений в гидратном слое. Сложный процесс гетероион-ного обмена - основной фактор, определяющий состав минерального компонента кости [11].

17-20 % и ширина на 5-9 % при неизменной толщине) [6, 7]. Подобные сдвиги вызваны соответствующими изменениями размеров собственно кристаллитов, их длины и ширины [21], причем размеры по А-оси меняются быстрее и сильнее, чем по С-оси [20].

В заключение теоретико-экспериментального обоснования модели следует указать, что она должна:

• 1)    удовлетворительно описывать снижение модуля упругости Е_кт по сравнению с модулем упругости Е ап ;

• 2)    учитывая наличие структурированной воды, дать теоретически обоснованную оценку ее модуля упругости Е_вод ;

• 3)    обеспечить понимание условий возникновения первичных микроповреждений;

• 4)    указать причины уменьшения прочности и увеличения хрупкости костной ткани при старении организма;

• 5)    дать теоретически обоснованную оценку снижения модуля упругости костной ткани Е_кт при старении.

Общие характеристики элементов физико -механической модели

Гидратный слой. Обозначим толщину этого слоя t (рис. 1) . Каждый из двух расположенных рядом кристаллитов окружён своим гидратным слоем. Поэтому толщина разделяющей их водной плёнки составляет 2 t или 1,3 нм, что соответствует 6-10 размерам молекул воды [11].

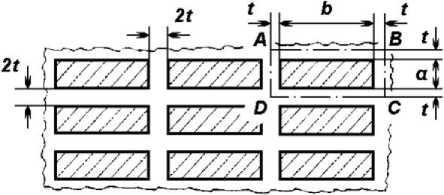
Рис. 1. Схематическая организация минерального матрикса на уровне отдельных кристаллитов с учетом структурированной воды. Обозначения: t - толщина слоя жестко связанной структурированной воды вокруг одного кристаллита; 2t - расстояние между двумя кристаллитами; a, b - толщина и ширина кристаллита соответственно; ABCD - фрагмент, являющийся структурной основой механической модели

Гидратная пленка (адсорбат) жестко сцепле- на с кристаллитами (адсорбент) [11]. В результате адсорбции минимум один слой молекул адсорбата остается неподвижным при внешнем механическом воздействии [18]. В рассматриваемом случае пленка имеет несколько подобных слоев, так как молекулы воды, обладая существенным дипольным моментом, выстраиваются «в цепочки» под действием электрического поля поверхностно расположенных ионов кристаллита. Такое структурирование дополнительно стимулируется тем, что водный раствор насыщен ионами фосфата и кальция, одноименными с ионами кристаллической решетки адсорбента. В итоге структура водной пленки имеет много общего с кристаллитом и по своим механическим свойствам приближается к твердому телу, что проявляется, в том числе, увеличением плотности этого раствора. В некоторых случаях она достигает значений в 10 % и более на расстоянии 1-2 молекулярных диаметров адсорбата от кристаллической поверхности адсорбента [18]. В результате по сравнению с обычным раствором гидратированный слой, содержащий ионы фосфата и кальция, ведет себя как твердое тело и демонстрирует высокое сопротивление не только отрыву от кристаллита, но и отрыву составляющих его частиц друг от друга.

По мере старения, как уже отмечалось выше, происходят изменения структуры гидратного слоя и соответствующие сдвиги кристаллической решетки минералов (нестехиометрические замены ионов фосфата на ионы карбоната и так далее). В результате снижается прочность гидратного слоя, так как изменяется характер межмолекулярных связей как внутри него, так и между элементами гидратного слоя и кристаллита.

«Пористость» костных структур. Этот термин в настоящей работе носит отличный от общепринятого смысл, так как рассматривается с точки зрения механических свойств. Для количественной оценки механической пористости весь объём кости разделяется на две части. Первая вбирает в себя минеральную составляющую, лимитирующую жесткость и прочность костной ткани, вторая объединяет остальные компоненты, которые не оказывают существенного влияния на эти механические свойства и поэтому определены как «поры».

При первоначальной оценке степени пористости исходим из того, что доля минерального компонента (золы) составляет в костной ткани около 50 % по массе, то есть в 1 кг кости имеем 0,5 кг минерального компонента и 0,5 кг - органического компонента и воды. Плотность ρ гидроксиапатита находится в пределах 30003200 кг/м³ [10, 15], плотность коллагена примем равной плотности воды, то есть 1000 кг/м³. В этом случае 0,5 кг минерала имеет объём 0,5/3,2 = 0,156 л, 0,5 кг органики и воды = 0,5 л, а суммарно органика, вода и минерал = 0,656 л.

Таким образом, объёмная доля минерала (0,156/0,656)×100 = 24 %.

Отношение объёма гидратного слоя к объёму кристаллита составляет 1,9 [11]. Так как относительный объём минерального компонента равен 24 %, то относительный объём гидратных слоёв 24 % × 1,9 = 46 %. Соответственно минерал и связанная с ним вода занимают 24 % + 46 % = 70 % объёма костной ткани. Оставшиеся 30 % объёма приходятся на свободную воду, органические структуры и связанную с ними воду, которые с механической точки зрения в настоящем исследовании рассматриваются как «пористость» (см. выше).

Если исходить из двухфазной механической модели J. D. Currey [23] и того факта, что объёмное содержание минерала и жестко связанной с ним воды в костной ткани составляет 70 %, то, следовательно, величина E кт должна быть на уровне 70 % от значения E ап . Согласно же представленным выше экспериментальным данным отношение упомянутых модулей упругости находится в пределах от 18 % до 30 %. Этот факт легко объяснить, учитывая дополнительную податливость водных прослоек, входящих в состав минерального «монолита».

Что же в этой связи происходит при старении? Данных об изменении толщины гидратного слоя мы не нашли, в то время как множество авторов, как было сказано ранее, отмечают рост размера кристаллитов. В настоящей работе исходим из того, что толщина гидратного слоя остается неизменной.

Описание модели

Для дальнейших расчетов, основываясь на описанных выше параметрах, примем за норму следующие исходные размеры кристаллитов, имеющих форму прямоугольного параллелепипеда: толщина ( a ) - 4 нм, ширина ( b ) - 8 нм, длина ( l ) - 14 нм . Первоначально обратимся варианту, при котором все кристаллиты располагаются правильными рядами (рис. 1), при толщине водной плёнки между ними 2t = 1,3 нм . Локус ABCD , включающий в себя один кристаллит с окружающей его водной плёнкой, является по существу наноуровневой структурой.

Продольная сила N (рис 2) сжимает или растягивает рассматриваемый локус. Исходя из гипотезы, что в этом элементарном локусе водная пленка ведёт себя подобно твёрдому телу со специфическими механическими свойствами, рассмотрим механическую стержневую модель, состоящую из двух параллельных стержней (рис. 2, а). Первый сформирован водной пленкой и представляет собой трубку прямоугольного сечения с площадью Авод и длиной l + 2t. Внутри этой трубки расположен второй стержень (с площадью сечения Аап), который состоит из двух последовательных участков, первый длиной l – кристаллит гидроксиапатита с моду- лем упругости Eап и второй – водная прослойка длиной 2t с модулем упругости Eвод. Здесь две водные плёнки, относящиеся к торцевым поверхностям, условно сведены в один слой удвоенной толщины 2t (рис. 2, б).

Продольная сила N деформирует всю рассматриваемую модель и имеет две составляющие N вод и N ап , (рис. 2, б):

N = N вод + N ап . (1)

Сила N_вод деформирует водный столбик (водную трубку), сила N_ап – внутренний составной стержень.

Под действием силы N первый и второй стержни деформируются совместно, одинаково изменяя свою длину (рис. 2, б):

Ah = Ah. (2)

Для предварительных расчетов предположим, что модуль упругости водной плёнки Е вод соответствует модулю объёмного сжатия воды К при температуре 40 ° C и атмосферном давлении. По справочным данным имеем Е вод = К = 2,3 ГПа [17]. В этом случае Е вод меньше модуля E ап в 20-40 раз. Исходя из формулы (2) путём несложных выкладок получаем, что сила N_ап превосходит силу N_вод более чем на порядок. Это позволяет пренебречь величиной N_вод и для упрощения дальнейших рассуждений принять ее равной нулю.

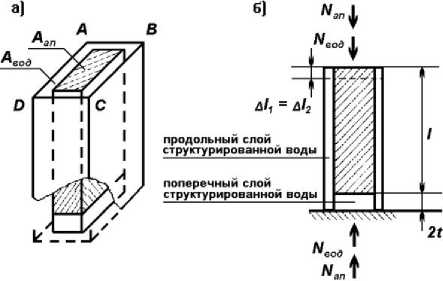
Рис. 2. Фрагмент ABCD (рис. 1), представляющий единичный кристаллит, окруженный структурированной водой: а) – аксонометрическая проекция; б) – продольное сечение. Обозначения : l – длина кристаллита; Δl 1 – деформация продольной водной пленки; Δl 2 – суммарная деформация кристаллита и поперечной водной пленки; N вод – продольная сила, деформирующая воду, расположенную в продольном направлении; N ап , – продольная сила, деформирующая минерал и воду, расположенную в поперечном направлении; А ап – площадь поперечного сечения кристаллита; А вод – площадь поперечного сечения продольной водной пленки

Величина Al₂ представляет собой сумму деформаций стержня, состоящего из минерала и поперечной прослойки воды. Так как они соединены последовательно, то силы, действующие на них, одинаковы, как одинаковы и их площади сечения. Следовательно, исходя из закона Гука [5, 13] получаем:

Al 2 = N an l/(E an A an ) + N an (2t)/(E eo A an ).   (3)

В связи с тем, что мы пренебрегли силой

N_вод , имеем N_aп = N . В этом случае формула (3) принимает вид:

А 2 = Nl/(E а A ап ) + N(2t)/(E eog A an ).    (4)

При экспериментальной оценке Е_кт костная ткань рассматривается в виде гомогенной структуры. В этом случае закон Гука для элементарного локуса записывается следующим образом:

Al = (N/E kT )((l+2t)/(A eod +A an )).      (5)

Здесь символом Al обозначена продольная деформация этого локуса при условии:

Al = Al₂.                      (6)

Исходя из этого, приравняем выражения (4) и (5) и, проведя преобразования, найдем выражение для расчета модуля упругости водной плёнки:

Е вод = E km (2t/(1 + 2t))((A eod + A an )/A an )(1/C), (7) где:

C = 1 - (E_Km/E_an)(l/(l + 2t))((A eod + А ап )/А ап ). (8)

Вычислим значения площадей поперечного сечения центрального стержня ( A ап ) и окружающей его трубки ( А_вод ):

A ап = ab = 4×8 = 32 нм²,

А вод = (2t+b)(2t+a)-A an = (1,3+8)(1,3+4)-32 = = 17,3 нм².

Подставляя полученные значения площадей в формулы (7) и (8), находим:

C = 1 - 1,54(Ект/Еап)(./(. + 2t),(9)

Евод =1,54Ekm(2t/(l + 2t))(1/C).(10)

Далее с учетом значений 2 t = 1,3 нм и l = 14 нм формулы (9) и (10) принимают вид:

C = 1 - 1,409(Ект/Еап),(11)

Евод = 0,131Ект(1/С).(12)

Как отмечено выше, отношение Е_кт/Е_ап составляет в среднем 0,24. Подставляя это значение в формулы (11) и (12), получаем:

C = 1 - 1,409 х 0,24= 0,662,

Е вод = 0,131Е кт (1/ 0,662 )= 0,198 Е кт .

В дальнейших расчетах исходим из того, что Е_кт = 15 ГПа [26]. Поэтому, подставляя данное значение в последнюю формулу, определяем величину модуля упругости ультратонкой водной плёнки:

Е_вод = 0,198x15 = 2,97 ГПа.

Полученное значение модуля упругости гидратной плёнки Е_вод всего на 29 % отличается от модуля объёмного сжатия свободной воды К , что вполне укладывается в интервал случайного разброса тех экспериментальных данных, которые мы положили в основу расчёта.

Подводя итоги проведённого здесь анализа, можно утверждать, что предлагаемая трёхфазная модель удовлетворительно объясняет снижение модуля упругости Е_кт костной ткани в 35 раз по сравнению с модулем упругости Е_ап гидроксиапатита. Следовательно, первое регламентирующее условие выполнено.

Изменение параметров модели при старении

Вернёмся к уравнениям (4) и (5), вновь приравняем друг к другу их правые части согласно условию (2), а затем полученное уравнение разрешим относительно модуля упругости Ект костной ткани. Результат можно представить в следующем виде:

Е кт =Е aп ((l+2t))/(l+2t Е ап /Е вод ))(А ап /(А ап +А вод )). (13)

Выше было указано, что с изменением возраста от 35 до 75 лет средние значения длины l и ширины b увеличиваются примерно на 20 % и 9 % соответственно. Толщина а кристаллита и толщина 2 t водной плёнки не изменяются. В итоге имеем новые значения параметров уравнения (13):

l = 14 x 1,2 = 16,8 нм, b = 8 x 1,09 = 8,72 нм , А ап = ba = 8,72 x 4 = 34,9 нм², А вод =(b+2t)(a+2t)-А aп = (8,72+1,3)(4+1,3)-34,9 = = 18,2 нм²,

Эти новые значения параметров подставляем в формулу (13). Кроме них в формулу также вводим значение Е_ап = 65 ГПа [26] и значение Е_вод = 2,97 ГПа, полученное в результате вышеприведенных расчетов. Введение этих численных значений в формулу (13) позволяет найти теоретически рассчитанное на основании предлагаемой модели соотношение модулей упругости старческой костной ткани к гидроксиапатиту:

Е кт = Е ап ((16,8+1,3)/ /(16,8+1,3 x 65/2,97))(34,9/(34,9 + 18,2)) = 0,26 Е ап .

Как уже отмечалось выше, согласно экспериментальным данным при старении (после 35 лет) это отношение снижается от 0,24 до 0,215 [32]. В наших же теоретических расчетах установлено, наоборот, увеличение отношения модуля упругости костной ткани к модулю упругости гидроксиапатита с 0,24 до 0,26. Это, казалось бы на первый взгляд, несоответствие расчетных данных экспериментальным становится понятным, если учесть тот факт, что в эксперименте определение модуля упругости оценивается по достаточно большому костному фрагменту. А согласно данным Martin, R. B. [27] при старении увеличивается пористость костных структур, которая, по нашему мнению, и является причиной снижения модуля упругости на фоне увеличения хрупкости костной ткани.

Жёсткость костной ткани и винтовые структуры

В предыдущем разделе рассмотрен вариант, при котором продольная ось кристаллита совпадает с направлением господствующих в кости растягивающих или сжимающих сил. Однако в естественных условиях это совпадение встречается редко в связи с наличием винтообразной иерархической организации минерального матрикса. Именно это создает условия, при которых продольное направление рассматриваемого выше элементарного локуса костной ткани не всегда совпадает с направлением господствующих растягивающих (сжимающих) усилий (рис. 3 и 4). В результате возникают касательные (сдвиговые) напряжения т, направленные вдоль поперечной водной плёнки. В зависимости от угла ф касательные напряжения могут варьировать (см. ниже).

При наличии касательных напряжений т прямоугольный элемент деформируется путём искажения прямых углов (рис. 3). Соответствующий угол искажения у принято называть углом сдвига. Величины т и / связаны законом Гука:

Y = т/G. (14)

Здесь G - модуль сдвига, который всегда существенно меньше модуля упругости Е, и поэтому проекция абсолютного сдвига на направление господствующей растягивающей (сжимающей) силы становится значимой. Эта проекция на рис. 3 обозначена символом А.

На рис. 3 изображена лишь деформация сдвига водной прослойки, хотя в гидроксиапатите возникают точно такие же касательные напряжения. Дело в том, что модуль сдвига упомянутого слоя весьма невелик даже в условиях значительных сил адсорбции. Именно ввиду малости модуля сдвига водного слоя имеем заметную сдвиговую деформацию этого слоя.

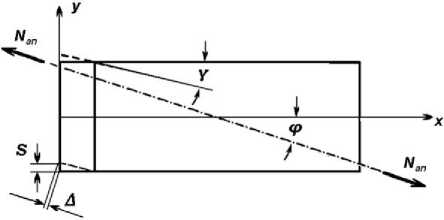
Рис. 3. Схематическое изображение возникновения дополнительных продольных деформаций в результате сдвига по водной прослойке. Обозначения : N ап – внешняя нагрузка; φ – угол несовпадения продольной оси ( х) кристаллита и направления действия силы; y — угол сдвига; 5 - абсолютный сдвиг; J - проекция абсолютного сдвига по направлению внешней нагрузки; у - поперечная ось

Упомянутую проекцию деформации А на направлении N следует складывать с аналогичной проекцией А деформации поперечной водной пленки, которая была учтена выше в качестве фрагмента уравнения (4): А = N(2t)/(E_eодA_ап). Деформация А определяется нормальными напряжениями о, деформация А - касательными т Возрастающую суммарную деформацию ( А + А¹) следует считать причиной еще большего увеличения податливости модели (т. е. костных структур) в направлении господствующих сил N .

В этих обстоятельствах по-новому представляется роль винтовых (спиральных) структур в кости. Именно подобная структурная организация дополнительно увеличивает податливость костной ткани за счет деформации сдвига водных плёнок. В этой связи важен тот факт, что это сдвиговое деформирование структурированной воды на наноуровне возникает при лю- бом типе деформации кости (сжатие, растяжение, скручивание, изгиб), происходящей на макроуровне. И в этих условиях, по нашему мнению, доля сдвиговых деформаций имеет один порядок с деформацией растяжения-сжатия. Повышение деформируемости костной ткани, в свою очередь, увеличивает производительность системы, обеспечивающей движение жидкости в канальцевой системе, то есть улучшает процесс поступления питательных веществ к остеоцитам и удаления от них шлаков.

Таким образом, можно говорить о создании усовершенствованной, более сложной модели элементарного локуса. Эта модель, помимо деформации растяжения-сжатия гидратной плёнки, должна учитывать её деформацию сдвига. Однако в данном случае возникают существенные технические проблемы, а именно: в настоящее время не известны не только значения модуля упругости и модуля сдвига гидратной плёнки, но даже их соотношение. В изотропном твёрдом теле отношение k = E/G находится в пределах от 2 до 3 [5, 13]. Параметры структуры и физических свойств гидратной плёнки близки к аналогичным параметрам твердого тела, но не достигают их. Поэтому отношение k должно быть существенно больше 3. В этих условиях податливость предложенной здесь трехфазной модели будет соответствовать податливости реальной костной ткани, если принять модель упругости водной прослойки Е_вод превосходящим значение, которое было использовано в наших вышеприведенных расчетах Е_вод ≈ К ≈ 2ГПа. Высказанные здесь предположения не противоречат современным представлениям физики наноструктур. Однако все это требует экспериментальной проверки.

Инициация первичных локальных разрушений структуры минерального матрикса на наноуровне при изменении условий нагрузки. Для понимания механизмов инициации повреждений на наноуровне предлагаемую трёхфазную механическую модель удобнее рассматривать с помощью схемы, представленной на рис. 3 и 4. Здесь нет продольного водного слоя, потому что он практически не оказывает влияния на ход процессов деформирования в поперечной водной плёнке.

На рис. 4, а внешняя сила N приложена к модели строго по её продольной оси x . В подобной ситуации возникающая по поперечному сечению (в гидратном слое) внутренняя сила равна и параллельна внешней силе и направлена по нормали (перпендикуляру) к этому сечению. Степень воздействия внутренней силы на материал характеризуется напряжением (сила, приходящаяся на единицу площади). В данном случае - это нормальное напряжение ст, которое рассчитывается по формуле [5, 13]:

СТ = N/А ап. (15)

С учетом свойств гидратного слоя, располагающегося между двумя кристаллитами, необходимо еще раз подчеркнуть, что он демонстрирует высокое сопротивление отрыву или, другими словами, для его разрушения необходимо создание относительно больших нормальных напряжений. Несколько другая ситуация складывается при действии внешних сил под углом Ф к продольной оси кристаллита (рис. 4б). Здесь в поперечном сечении стержня возникают, как сказано выше, помимо нормальных напряжений г еще и касательные т Между ними в данном случае имеется следующая зависимость [5, 13]:

т = 0,5 г sin 2 ф.

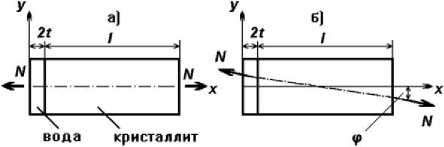
Рис. 4. Схематическое изображение двух вариантов направления действия нагрузки по отношению к продольной оси кристаллита: а) направление действующей силы совпадает с продольной осью кристаллита; б) направление действующей силы не совпадает с продольной осью кристаллита. Обозначения : l – длина кристаллита; 2t – толщина водной плёнки; N – внешняя нагрузка; φ – угол несовпадения продольной оси ( x) кристаллита и направления действия силы; y – поперечная ось

Это крайне важно, так как в результате винтовой иерархической организации костных структур при любом направлении нагрузки значительная часть кристаллитов находится в условиях, иллюстрируемых схемой 4б. Параметры многоуровневых винтовых структур в реальной кости таковы, что угол ф может достигать 10 -20°, а в отдельных случаях 40° и более. В этих обстоятельствах из формулы (16) получаем, что касательные напряжения т могут достигать значительных величин (до половины нормальных). А в связи с тем, что водная прослойка сопротивляется срезу под действием касательных напряжений значительно слабее, чем отрыву под действием нормальных напряжений, высока вероятность локального возникновения критических ситуаций, при которых происходят эле- ментарные акты повреждения в виде среза по водным прослойкам.

По мере роста нагрузки эти повреждения сначала возникают лишь в тех локусах, где угол наклона ф максимален. В результате нарушается локальная целостность единого минерального массива и происходит уменьшение эффективной с механической точки зрения площади поперечного сечения кости. Последнее немедленно ведёт к росту среднего уровня напряжений в костной ткани, что повышает опасность дальнейших повреждений. Кроме этого вблизи повреждений искривляются траектории господствующих растягивающих и сжимающих напряжений. Это, в свою очередь, в отдельных локусах приводит к дальнейшему увеличению угла ф (рис. 4), то есть критичность ситуации обостряется. Таким образом, можно утверждать, что один и тот же механизм, определяющий жесткость костных структур, при определенных условиях лежит в основе инициации повреждений этих же структур на наноуровне.

Снижение прочности и жесткости костной ткани при её старении. Выше было сказано, что с возрастом в кристаллической решётке гидроксиапатита происходят всякого рода нестехиометрические замены одних ионов на другие. К числу наиболее существенных факторов относится замещение ионов фосфата на ионы карбоната. Аналогичные изменения происходят в гидратном слое, представляющем собой насыщенный водный раствор, который по химическому составу близок к минеральному компоненту. Указывалось также, что гидратный слой находится в особых условиях, при которых его физические свойства напоминают твёрдое тело, более того – монокристалл. В этих обстоятельствах нестехиометрические замены вызывают дефекты его структуры, приводящие к уменьшению силы межмолекулярных связей и соответственно к уменьшению сопротивления сдвигу. В результате отмечается снижение всех прочностных и жесткостных характеристик. Именно изменение химического состава гидратного слоя, а не гиперминерализация костной ткани является первопричиной ухудшения прочности и уменьшения жесткости кости.

ВЫВОДЫ

• 1.    Разработана трёхфазная наноуровневая модель элементарного локуса костной ткани, согласно которой гидратный слой воды, разделяющий кристаллиты гидроксиапатита, лежит в основе механизма, определяющего жесткость костных структур в физиологических условиях.

• 2.    Данная модель предполагает, что этот же механизм лежит в основе инициации разрушения костных структур на наноуровне при изменении характера нагрузки.

• 3.    Разработанная модель элементарного локуса костной ткани на наноуровне удовлетворительно описывает связь между модулем упругости гидроксиапатита и модулем упругости костной ткани на макроуровне.

• 4.    Гидратный слой воды способен воспринимать не только сжимающие и растягивающие усилия, но и усилия сдвига. В этих обстоятельствах трёхфазная модель элементарного локуса обеспечивает понимание условий разрушения костной

• 5.    Предлагаемая модель объясняет необходимость существования винтовых (спиральных) структур в костях оптимизацией функционирования конвекционного механизма движения жидкости в канальцевой системе.

• 6.    Снижение прочности и жесткости кост-

• ной ткани согласно анализу модели вызвано гетероионными заменами, происходящими в гидратном слое при старении организма, а не гиперминерализацией костной ткани.

• 7.    Трёхфазная модель указывает на теоретические предпосылки создания новых конструкционных материалов с особенностями строения на наноуровне.

ткани на самом низком иерархическом (молекулярном) уровне путём среза по гидратному слою.