Механизмы начального разрушения железобетонной крепи сферической горной выработки в массиве осадочных пород

При сооружении горных выработок, представляющих собой сферические полости, подкрепление является одним из основных производственных процессов, без которого невозможна их эксплуатация. Крепи, предназначенные для обеспечения безопасности труда, сохранности находящегося внутри сырья и оборудования, как правило, изготавливаются из железобетона и являются массивными сооружениями. Поскольку железобетон и горные породы имеют ярко выраженную анизотропию свойств, вызванную наличием стержневых армирующих элементов и минеральных включений, важным и актуальным является получение новых точных аналитических решений краевых задач о равновесии толстостенных составных анизотропных упругих тел с центральной симметрией, находящихся под действием равномерного внутреннего и внешнего давления в поле гравитационных сил, и разработка на основе этих решений инженерных методик уточненного прочностного анализа элементов конструкций и сооружений, имеющих аналогичную геометрию и граничные условия. Кроме того, эти решения могут использоваться для идентификации материальных постоянных и функций анизотропных материалов (железобетон крепи создается вместе с самим горным сооружением) и при тестировании алгоритмов, реализующих численные методы, а также при отработке методик экспериментов с «тяжелыми» телами простейшей геометрии.

Рассмотрим равновесие составного линейно-упругого анизотропного сферического тела, представляющего собой конструкцию, состоящую из двух полых толстостенных сфер с общим центром, жестко закрепленных по внешней поверхности радиусом ρ2 и находящихся под действием равномерно распределенного по внутренней поверхности радиуса ρ1 давления в поле гравитационных сил. Будем считать, что поверхность контакта, на которой выполняется условие идеального сопряжения, находится на расстоянии ρc от центра, а материал, из которого изготовлено составное тело, однородный, сферически трансверсально-изотропный относительно любого радиуса-вектора, проведенного из геометрического центра. Будем использовать сферическую r, 0 и ф систему координат. Все константы и функции, относящиеся к внутренней части составной сферы, будем обозначать верхним индексом 1, стоящим в скобках, а к внешней – индексом 2 соответственно. Радиальные и окружные перемещения ( ur(*) и u0(1)), радиальные (*)         „(*)                                          (*)         „(*)                                                             (*)              *)

(сД и Err), окружные (C00 и 800), меридиональные (афф и 8фф ) напря жения и деформации, касательные напряжения т* и сдвиговые деформации 8^0 не зависят (в силу симметрии тела и внешней нагрузки) от меридиональной координаты ф, удовлетворяют геометрическим соотношениям Коши

⁽ * ) ₌ rr

д u r * ) д r

8( * )- 1

⁸ 00 =

r

U r V

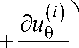
⁸ ф * ф = r ( u 0 * ) ctg ^{0 +} u r* ) ) , Y r s

д и ⁽⁰ 1 (д и ^{( f )} (*■/ --— +--- и 0 )

д r   r д0

V          7

i = 1 или 2

и уравнениям равновесия

( * )  V^(0                            А

^^ rr - + ¹     r ⁰ + 2g⁰? - о (⁰ - G * ) + тфд * ctg 0 + F ( * ) = 0,     (2)

дr    г V д0 фф 00    r0      J r дТ r 0 + 1 д r r

дст99 ""де”

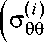
-^ ф ^г ф ) ctg ⁰⁺ 3 ^T r 0

+ F ₀^(O = 0.

Здесь F r ) = —y ^{( z )} cos 0 и F 0 ) = y ⁽ * ) sin 0 - компоненты вектора массо-

.      „( * )

вых сил, Y — удельный вес материала.

Определяющие соотношения для сферически трансверсальноизотропного тела п (*•)     (ОД*)     (*) (*)    (*)     (0_/) Д*) OLO)     (ОД*)

^G rr A 11 ⁸ rr ⁺ A 12 ( ⁸ фф ⁺⁸ 00 ) , ^с фф A 12 ⁸ rr ⁺ A 22 ⁸ фф ⁺ A 23 ⁸ 00 ,

_п ( * )       (О)     (%( * )      (%( * )    ( * )      ( * )Д * )

^G 00     12 ⁸ rr ⁺   23 ⁸ фф ⁺   22 ⁸ 00 , ^т r 0     44 ⁸ r 0

можно записать с помощью технических постоянных

( i )

а ( - )= E_u __u( i n л( i ) ₌

11 M 1^{1 р} 6ф / , ^22

v ⁽) ^{x          7}

E ⁽‘)

E 6

0") , 0") 0") ^v() +p 6^^v()

F ( i )A ^{( i ) 2} E^ ^{1 p} r ⁶ ( i ) ,

⁽ i )- A 23

E ⁽ i )

(i) (i) (i) ^р 6ф ^+р -e (i) ^Er.

( i )

Г ( i ) ( i ) 2 E-

г ( i )

_Л( i ) - E^u ( i )

, ^12       (Л ^p r 6 ,

v()

F (‘)

_Л ( i )__G( i ) _v( i )-Д-и(1)_7и( i ) 2 E^ A 44 G r 6 , ^{V 1 р} 6ф ^{2 p} r 6 ( i ) ,

r определяемых модулями Юнга еГ 1) и E61) в направлениях r и 6, коэффициентами Пуассона p-r) и Ц(6ф, а также модулем сдвига G^:6,1 в диаметральной плоскости.

Так как находящееся в поле гравитационных сил толстостенное составное сферическое тело с жестко закрепленной внешней поверхностью находится в равновесии, то u?\    = 0, u62)|

¹Г =P 2                  ^lr =P 2

= 0, ^^

¹ r =Р 1

= 0,^У   = ^- P ,

¹ r =Р 1

и, ^И|    = ur^2,|

^1r =Р c            ¹

c

, u 6 1*1

= - 6 2'1

^, c

T (1)l

^T r 6

c

=t ⁽²⁾|

^T r 6 |

c

, О ⁽¹⁾|

, _rr

= G ⁽²⁾| rr

.

c

Последовательная подстановка геометрических соотношений (1) в определяющие (3), а затем полученного результата – в уравнения равновесия (2) позволяет записать неоднородные системы дифференциальных уравнений Ламе в частных производных [1, 2]:

»Z u 21

A 11 Я 2 ⁺ 5 r r

2 A^

¹¹ 5 r

5 ² u ^{( i} ) 5 u ^{( i} )        )

--+^ ctg 6 +

(5 r 56   5 r     J

1 r ²

A

2 ( i

( i ) 5 u r

5 u ⁽⁾

₍ 56 ²     56

■ ctg 6 + 2 ( A ( 2 ) - A 2x A 2 i ) )

I u r ) +

,(_Л (0__Л())__Л())__Л(0\ ( ^12 ^22 ^23 ^44 )

^Z 5 u 6° ( ^д6

+ u 6 i ) ctg 6 =у ^{( 1}) cos 6 , /.

A ⁽ i )

A ₄₄

d ² u ' ) 1

⁰i d r ² r

2 A 4 4 d r U O '

d u 2 ) d r

i

( A 12 ⁺ A ₄₄ )

5 ² ur¹ )

d r 50

i

+-1т

r 2

A ⁽ i )

A 22

" s ² u 0 ' ) + a u O ' ) dO ^{2 +} dO

ctg O^+ ( A 2 »+ A 23 + 2 A ^ ^x                 ’ SO

-( A 5 + 2 A P? + A У ctg ² 0) u ⁽ ' ) l=-y⁽ ' ) sin 0 ,

23          44 22 O

Решение в силу симметрии задачи может быть представлено в виде тригонометрических рядов [1–5]:

TOTO ur') = Eurn(r)cosnO, uO') =2u0'n(r)sinnO .(6)

n=0

При подстановке выражений (6) в (5) и (4) получим бесконечное число систем обыкновенных дифференциальных уравнений вида

(i)   „('■)        (i)  1    ,(i)        (i)   1      (i)        (i) 1    ,(i)        (i)   1      (i)

a , n u ' n + a 2 n -u rn + a 3 n ~u rn + a 4 n -u O n + a 5 n ~u 0 n = A n , rr rr

(' )u"('') +h(') —u') +b(') 1/(') +b(') —u,(') +b(') w(')-B(') b1 nu0n + b2n u0n + b3n 2 u0n + b4n urn + b5n 2 urn Bn , rr rr где

a( n’= A1(1), a 2n= 2 A^), a 3 n= 2(A(2)-A 2 i)-A 25)-A4'?(n2 + nctg 0 tgn 0), a4'n =( A12) + A44t))(n+ctg 0 tg nO),

n(0 Дл(') _ j(i) _ .(') _ л(')           a a5n I A12 A22 A23 A44 Дn + ctg O tg nO) ,

b ⁽ ')=A ⁽ ' ) /)⁽ ' ) ⁼2t4⁽ ' ) 5⁽ ' ⁾⁼— j!⁽ ' ) 2j1⁽ ' ) j!⁽ ' Vи²—1—zzctsO cts/70+csc²O^ _n   ^44 , ^2 _n  ^^44 , ^3 _n    ^23       44  ^22 i n   ^{1  n c}tg  ^ctg n^ ^{+ csc}    1 ,

( ' )- j( i ) j( ' Ui     ( ' )- j( ' ) a(°+2a( '

^b 4 n    ( ^A 12 ^{+ A} 44 ) n , ^b 5 n    ( ^A 22 ⁺ A 23 ⁺ 2 ^A 44 ) n ,

A

( ' )

n

Y⁽ ' ) , n = 1, 0, n = 0, n > 1,

B ⁽ ' ) n

^ -y⁽ ' ) , n = 1, 0, n = 0, n > 1,

с соответствующими граничными условиями ur?|    = 0,u.'I

I r =P2                 I

-о Л( ¹ )_м'( ¹ )-4( ¹ ) 1и ( ¹ )-Л( ¹ ) Пи ^{( 1 )}

0, A 44 u 9 n A 44 u 9 n A 44 u rn

(1)?,/,(1) z^1      (1)       (1)

A 11 u rn ⁺ A 12   u rn ⁺ A 12 ( n ⁺ ctg ^{9 tg} n

r

r

' 9) ¹ u 2

r

r

=0, r=P1

^r =p ,

- P , n = 0, 0, n >  0.

u™|    = ur?|    ,u92|    = u9^1

Ir=pc           \r=pc         lr=pc           lr=pc j (1)M'(1)_ j(1) L (1)_ j(1) nu (1)

A 44 ^u 9 n A 44 ^u 9 n A 44 u rn rr

-А              1u ( 2 )-//( 2 ) n i/( 2 )

A 44 ^u 9 n A 44 ^u 9 n A 44 u rn rr

(Du^¹) /1)²/1)              tPwA^¹/)

A 11 urn ⁺ A 12 urn ⁺ A 12 ⁽ n ⁺ c^{tg 9 tg} n ⁹⁾ u 9 n rr

= д ( 2 ),/( 2 ) + л( 2 )²,( 2 ) + 4( 2 )f и+ctP А tPMA^¹/2)

A 11 u rn ⁺ A 12 u rn ⁺ A 12 ( n ^{+ ctg 9 tg n 9)} u 9 n    .

r =P 2

Поэтому вычисление перемещений, деформаций и напряжений связано с решением n самостоятельных задач. Заметим, что для n > 1 однородные системы дифференциальных уравнений (7) дополнены однородными граничными условиями (8). Следовательно, все эти системы имеют единственное тривиальное решение: u r^ 0 и и 9 n = 0. Таким образом, задача может быть сведена к решению системы (7) с граничными условиями (8) при n = 0 и n = 1 [1-4].

При n = 0 перемещение в меридиональном направлении и 9 , ^: . 0, а система уравнений (7) значительно упрощается:

д ⁽ i ⁾_u"⁽ i i )+2/4⁽ i ) 1и ' ii ⁾+2f ^⁽ i ⁾-A⁽ i i ⁾-A⁽ i i )(—w^{( i} ) -0 A 11 u r 0 ^{+ 2} A 11 u r 0 ^{+ 2}I A 12 A 22 A 23 I ₂ u r 0 = 0^.

rr

Общее решение (9) выглядит следующим образом: u r '0= r ^{- 12 -} k ⁽° Л ■ r ^{- 12 +} k ⁽° D 2 ^{i )} ,

() /шТИг^^чЗ/^^^З^^^Т//^

^где ^ a! -¹/⁴ '²I A 22 ' A 23 A 12 I A 11

а из граничных условий (8) могут

быть определены постоянные интегрирования p212-^(2) D1 .p1 + ^(2) d 22)= 0,

D 1 ^{( 1 )} А 11 ^: | - 1'2 - 5 ^{( 1 )} ) + 2 A ? 2 p^{- 3/2 -} ' ^{( 1 )} +

+ D 2¹ ) A nl -b^+ 5 ^{( 1 )} ) + 2 A® p^{- 3/2 + 5 ( 1 )} =

^- P ,

р ^{- 12 -} - * D f+p Т* • ⁽" d 2^{1 )}=р ; 12 - s" d , ^|2)+p Т s^м d ?,

D f" [ A J? ( - 1/2 - - “' ) + 2. ; ,"^: A^-s " + + D 2" [ ^ S' (-V 2 + - ^№) + 2 ^ ,w ]p -«' s = = d *²¹ a !? ( - V2 - - ^{( 2 )} ) + 2 An p ; ^3/2- ' "+ + D 2^{2 )} A u)U/ 2 + - ^{1 2 |} ) + 2 An p. ^{- ,2)} .

При n = 1 имеем неоднородную систему дифференциальных уравнений (7), решение которой находим методом вариации произвольных постоянных. Тогда окончательно выражения для перемещений в толстостенной трансверсально-изотропной сфере запишем следующим образом:

м^ _п i ) _r ^- 1^{2 - -} . d (О _r ^- .

+ ( - C , i ’ + d 2 i ’ C 2 i ’ r ^{- 1} + d ₃ ^{( i} ’ C ₃ ^{( i} ’ r ^{- 12 +} t i + d 4 i ’ C 4 i ’ r ^- 1^{2 -} t i + H i ’ r ² ) cos 0 ,    (10)

u £’ = ,C,( i’ + C 2 i’ r-1 + C3(i’ r v2ti + C4i’ r -12-t10 + H0i’ r2 )sin 0, где

„ ( i )

⁽ i )-Л(//' i )-?/4⁽ i )-2^⁽ i )1 Я⁽ i )-^⁽ i ’ /4⁽ i ’

Hr Г,Ы\H    2A12 2A44 ) , H    A22 + A23, н 1 i ’

( i )

⁽ i )-Лf?/!¹' i)-H⁽-i )-2^⁽ i )^ L) )-2f/4⁽ i ) /4⁽ i )^ -A⁽ii)+2A⁽-i )^ ^H 0     tr( i ) \ A 11 ^{H    2} A 44 ) , ^L     \A 12 ⁺ A 44 ) A 11 ( ^{H + 2} A 44 ) ,

H ₁

t ⁽ i ’ - 9-1¹____ [ я⁽ i VJ⁽ i)+2A⁽-i ⁾'l-2J⁽ i VJ⁽ i)+3A⁽i )1

t А 4⁺ j( i ) zli. i ) ^H ( A 11 ^{+ 2} A 44 ) ² A 12 ( A 12 ^{+ 3} A 44 ) , 4 A 11 A 44

⁽ i )+2//⁽ i ’

, ( i ) = ^{H + 2} A 44

²             I¹ i ’ //' i ’ l¹ ‘ ’

A 12 H    A 44

d ⁽‘’ - ¹ [ У⁽ i ¹+ 2/I¹ i Л⁽ i ’ Л⁽ i ’V ¹ i ’ , d 3 = L i ) L ^{2  + 2} A 44 ( A 12 ⁺ A 44 ) t ] ,

d(i ’ — 1 [ У( i ’ — 2 A(i V 4( i ’ /I) i ’ V( i)! У( i ’ 4( i 4( i ’ —2H( i ’ —3 4( i ’'l d 4 Li) 2 2 A44 (A12 + A44 ) t , 2 A44 (A12 2 H 3 A44 ) , ij (i)-?[ Д( i )iH( i )-4A(i i )V24( i V H( i )-34( i )^-24( i)2

^H 1 ² A 11 l ^{H    4} A 44 l ^{+ 2} A 44 l ^{H    3} A 12 f ² A 12 ‘

Постоянные интегрирования C 1 ⁽ i ’ , C 2 i ’ , C ₃ ^{( i} ’ , C 4 i ’ , входящие в выражения (10), определяются из системы линейных алгебраических уравнений

C W 4 A ™' d ?' + ' ) + A , ' , ' d ₃ ^{( 1} '₍ 2 t ¹ ' - ! ) p¹-' t " + 2 C 2' ' 2 A *? ' d •1 ' + 1 ) - A , ³ , ' d 2^{; )} + + C^A$( d <^{1 )}+ 1 ) - A f d <' ⁾ ( 2 1 ™₊ ' ) ]p c”t " + 4 [ H ™' A f> + A^H” A «]p c = = 2 C 22 > [ 2 A .( d 2² > + 1 ) - A^d 22 > ]+ C <^{2 )}[ 4 A§ ( d <^{2 )} + ' ) + A®d 2 ( 2 1»' - 1 ) ]p "²*^P + +C ( ^{2 )}Г4А^{| 2 )}^^{| 2 )}+1'|-А^{| 2 )}А( ²⁾Ы² )+1А n^vi — t ^B+4[ H( ²)fA ^{| 2}) + 4( ² '1+ff( ² )A^{| 2} 'ln ^{3 +} C 4   ⁴ A 12 ' d 4 ^{+ 1} ) A ,, d 4 ' ² t  ^{+ 1} ) ^p _c    ^{+ 4} H r ' A ,, ⁺ A 12 ) ⁺ H 9 A 12   ^p_c ,

_rЗ²'+a(²M²V + /7(² )г( ²'п-^² + t^p)    r^:n^r 1 ^{( 2)} — н ( 2)02

C' + d2 C2 P2 + d3 C3 P2     + d4C4 P2        Hr P2 , c'2)+с22)p 21 + сp;V2*-M + с«W1--33 =-h92)p2,

- c ’ ¹ ' + d w с <' ⁾p - ' + d ®C (" p ; ¹² * t ' + d 4 с Wp . ¹² t " + H ^p 2 = =- с , ' ² ' + d®с 2^{2 )}p^{- 1} + d <” C 3² ' p^-121 t ^{( 2 )} + d 4 с 4² ' p - ^V2 - t " + H®p 2 ,

2 C ?>[ 2 a ;; ' ’ d ?⁾+ ' ) - A j? d '." p1" t ’“₊

+ C 3^{; )}[ 4 A ' ⁽ ; ' ( d <' > + ' ) + A f d ₃ ^{; )} ( 2 1 ™-1 ) ]p ' ^{+ 2} t " +

+ с 4¹'

4 A ,; ) ’ d 4" + i ) - a ,¹? d 4' ’ ( 2 1 ^(l)+ i ) ]p,=

Гя⁽¹'^ 4⁽¹'   л’^Кя’¹' J⁽¹' l d^7/2+ t ⁽¹⁾

4 Hr ’ A'1 + A'2 ) + H 9 A'2 p,    , с,'4+C«p-'+C3(1)p -12+t ” + C«p-;2-t(0 + H «p 2 =

= C      с 2² ' p^{- 1} + с 3 ^{( 2 )}p^{- 12 +} t ' ^{2 )} + с 4^{2 )}p^{- V2 -} t ' ^{2 )} + H 9 ² ' p 2 ,

2 с 2¹' ' d 2¹' + 2 ) p '^{2 +} t '° + C ₃ ⁽¹⁾ ' 2 d ₃ ⁽¹⁾ - 2 1 ⁽¹⁾ + 3 ) p ' ^{+ 2} t '° + + с 4^{; )} ' 2 d 4^{; )}+ 2 1 ^{( 1 )}+ 3 ) p , = 2 ' h 9 ¹ ' - h '¹⁾)p7^{/ 2 +} t ⁰⁾ ,

CA 4'4 ' d 2¹ ' + 2 ) - C 2² ' A 42 ) ' d 2² ' + 2 ) ]+ C3? A 4'4 ' 2 d 3? - 2 1 ⁽¹⁾+ 3 ) p y²⁺t ⁰⁾ +

⁽'Чн⁽¹'-H⁽¹'\ o³ J⁽''c⁽''f2(''+2/''+3'io'²- t

^{+ 2 A} 44 l ^Hr   ^H 9 l^p c ^{+ A} 44 C 4 I² d 4 ^{+ 2} t ^{+ 3} l^p c

= C ₃ ^{( 2 )} A 42 ' ' 2 d ₃ ^{( 2 )} - 2 1 ^{( 2 )} + 3 ) p c²⁺t ^{( 2 )} +

+2 A ^{( 2}' ( Я⁽²' - Я⁽²' о³ + 4⁽²'с⁽² ' ( 2d'²' +2/²' 'io'^2- t ^P)

+2 A44 I H r H 9 lpc + A44 C4 \ 2d4 + 2t + 3 Jpc , получаемых при удовлетворении граничных условий (8), и не приво- дятся ввиду громоздкости.

Последовательная подстановка уравнений (10) в геометрические

(1) и определяющие (3) соотношения позволяет записать выражения для радиальных

О« = 2 r ^{- 3/2 -} ' ¹⁰ { D^ 4 4 ' - A ® (1 + 2 5 ^{( i )} ) +

+ D 2 ' ' 4 a2 ' - 4 ) ( 1 - 2 5 ⁽ i ' ) r ^{2 5 W}} +

+ { 2 A 1 ⁽ 2 ’ ( 1 + d 2 i ' ) C 2 i ' r ^{- 2} + ( 1 + d ₃ ^{( i} ' ) C 3 ' r ^{- 3/2 + 1} +

+ ( 1 + d 4 ' ' ) C 4 ' ' r 3' ¹ + ( H ^ i ' + H 4° ) r -

- 1 A * ' Г?,/ * 'c^ * V ²+fl-2/⁽ ‘'W ' 'c⁽- ‘ V ^{3/21 1 4} ' ' + .^A 11 2 Lt 2 C' 2 •      + (1 ^2 1 ) 3 C ^ 3 r +

+(1+21(i))d4''C4''r-3/2-110 -4H4ir }cosO , окружных a» =4> = 1 r -3/2- 5 (i) {d4')Г2( A 4§ + Ag)-A4? (1+25 (z))!+ фф OO 2              1        22     23      12

+ D 2 ' ) 2 ( A 25 + A 2 3 ) ) - a 12 (1- 2 5 ^{( i )} ) r ^{2 5} ' } +

+ { ( A 22 + A 2 3 ) ) ( 1 + d 2 ' ) ) C 2 ' ) r ^{- 2} + ( 1 + d ₃ ^{( i )} ) C 3' r ^{- 3/2 +} t ¹⁰ + + ( 1 + d 4 ' ) ) C 4 ' ) r ^{- 3/2 -} t ¹⁰ + ( H ( ' + H O ' ) ) r -

- ¹ A '' Г 2 d 22 C 2' r ^{- 2} + (1 - 2 1 ⁽ ' ' VJ ' ' C ₃ ⁽ ' ' r ^{- 3/2 +} t^И +

2 12      2 2 у у 3 3

+(1+21('')d4''C4''r-3/2-110 -4H^r } cosO и касательных

т

⁽''—_4⁽'' ('")-^-l'I^'²\c^'² r o ^44 (2^+t< 2 2

r ^{- 2} +| 3 + d ₃ ⁽ ' ' - 1 ⁽ ' ' I c ⁽ ' ' r ^{- 32 + 1 И} +

1 2 ³ J ³

+f 2 + d 4 ' ' + 1 ⁽ ' ' J C 4 ' ' r ^{- 3/2 - 1 10} + ( H? - H O ' ' ) r

sin O .

напряжений.

Из полученных решений в частном случае, при замене E ( i ) = E ^i ) = E ( i ) , ц ( i ^p,^^ и G ( i ) = G^ ⁾= E ( i )l (2 + + 2 ц ( i ) ) , следуют выражения для напряжений, деформаций и перемещений в точках, находящихся в поле гравитационных сил полых и составных изотропных сфер с аналогичными граничными условиями [6, 7].

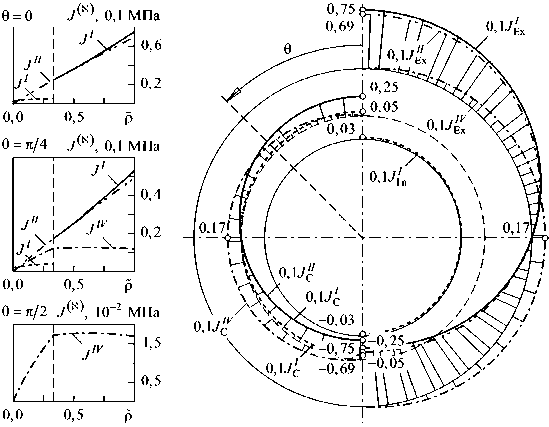
Рис. 1. Распределение инвариантов тензора напряжений на закрепленной внешней ( J E. ) ), свободной от нагрузок внутренней ( J ^ ) и контактной ( J^ ) поверхностях

Полученные аналитические решения (11)–(13) дают возможность анализировать вклад массовых сил в напряженное состояние железобетонных монолитных крепей сферических горных выработок, окруженных массивом осадочных пород, а также провести уточненную оценку начальной прочности и определить области, где может быть инициировано разрушение. Поскольку горные породы и железобетон имеют ярко выраженную анизотропию свойств, прочностной анализ элементов конструкций и сооружений, изготовленных из таких материалов, необходимо осуществлять на основе многокритериального подхода [6], рассматривая различные механизмы частичного или полного исчерпания несущей способности, характерные для анизотропных материалов. В работе [7] были введены независимые величины

J I =C66 , J II =O rr , J™ = ^( Cw-O66)2 + 4^ , J IV Ц Тф r +T2 r , инвариантные относительно ортогональных преобразований, допустимых над сферически трансверсально-изотропным телом, которые позволяют описать различные механизмы разрушения от растяжения или сжатия в окружном или меридиональном и радиальном направлении от сдвигов по поверхностям изотропии и в диаметральной плоскости соответственно.

На рис. 1 и 2 представлены распределения ненулевых инвариантов тензора напряжений J ^(к) в железобетонной сферической крепи ( E ₆= 40,0 ГПа, E r = 25,0 ГПа, G r ₉= 11,0 ГПа, ц_9ф = 0,075, p _{r 9} = 0,15 и у= 40 кН/м 3 ), окруженной массивом осадочных пород ( E ₉= 55,0 ГПа, E r = 23,0 ГПа, G r ₉= 29,0 ГПа, р_9ф = 0,29, p _{r 9}= 0,32 и у= 27 кН/м ³ ), при p = 0 МПа вдоль меридиональной и обезразмеренной радиальной координаты р= ( r -р ₁ )/( р 2 -р ₁ ) . Параметры геометрии были выбраны следующими: р ₁ = 2,5 м, р c = 3,1 м, р ₂ = 4,3 м (см. рис. 1) и р ₂ = 9,0 м (см. рис. 2).

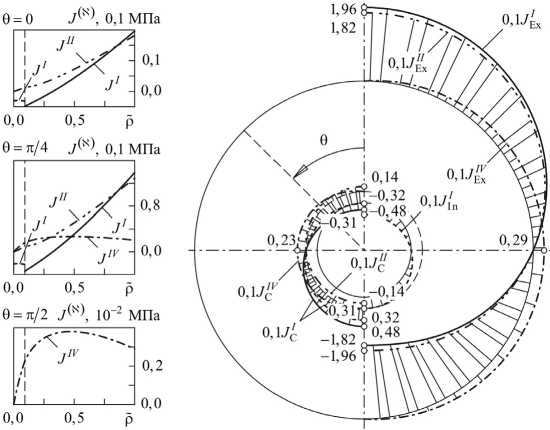
Рис. 2. Распределение инвариантов тензора напряжений на закрепленной внешней ( J EX ) ), свободной от нагрузок внутренней ( J ^ ) и контактной ( J (?^ ) поверхностях

Как видим, на свободной от нагрузок внутренней поверхности монолитной железобетонной сферической крепи ненулевым является только первый инвариант J^I , который нелинейно распределен вдоль р , принимает положительные значения в точках, принадлежащих своду, и имеет скачок на поверхности контакта. При заданных материальных константах существенное влияние на характер распределения J^I оказывает соотношение радиусов рассматриваемой крепи и окружающего массива осадочных пород. Так, например, увеличение толщины породного массива приводит к смене знака первого инварианта в железобетонной крепи.

Второй инвариант J^II при изменении радиальной координаты от свободной поверхности к закрепленной всюду возрастает по абсолютной величине, не принимая при этом в точках свода отрицательных, а в нижней полусфере – положительных значений. Поскольку в точках, принадлежащих вертикальной диаметральной оси, J^I и J ^II достигают своих наибольших по абсолютной величине значений, эти точки являются наиболее опасными с точки зрения возможности начала разрушения крепи от растяжения или сжатия в окружном и радиальном направлениях.

Третий инвариант J^III во всех точках железобетонной крепи и окружающего массива осадочных пород принимает нулевые значения. Следовательно, при заданных условиях нагружения и типе упругой симметрии материала механизмы разрушения от сдвига по поверхности изотропии не реализуются.

В точках, расположенных на вертикальной диаметральной оси четвертый инвариант J^IV равен нулю, возрастает по мере увеличения угла θ , достигая своих максимальных значений при θ=π 2 . Кроме того, в радиальном направлении от внешней поверхности монолитной крепи к внутренней J ^IV всюду убывает, достигая нулевых значений на свободной поверхности. Таким образом, наиболее опасными с точки зрения возможности начала разрушения крепи по механизму сдвига являются точки горизонтальной диаметральной плоскости.