Memory dependent response in an infinitely long thermoelastic solid circular cylinder
Автор: Lamba N.K., Deshmukh K.C.
Статья в выпуске: 1, 2024 года.
Бесплатный доступ
Memory-dependent derivatives (MDD) have physical meaning, and compared to fractional derivatives, they are more suitable and convenient for temporal remodeling. In this study, the temperature and stress distributions in an infinitely extended generalized thermally elastic solid circular cylinder have been investigated by utilizing the concept of a memory-dependent heat conduction model. The homogeneous, isotropic, infinitely long solid circular cylinder is considered to have a lateral surface that is free of traction and is subjected to a known surrounding temperature. In the domain of the integral Laplace transform, the problem is worked out, and its complex inversion is performed numerically using the Fourier series expansion method. The material properties of copper metal are chosen for the purpose of numerical computation, and the thermoelastic impact of time delay on temperature distribution, displacement distribution, and thermal stresses are represented graphically. Also, time delay's effect on temperature history, displacement history, and thermal heat transfer stress history are shown, respectively. This study could also benefit mathematicians and researchers involved in the development of thermoelasticity, as it accounts for the memory-related derivatives that are useful in explaining the behaviour of a variety of physical processes. The thermal fluctuations captured by various factors with memory-dependent responses are used in engineering applications to realistically design machines or structures.
Memory-dependent derivatives (mdd), solid circular cylinder, generalized thermoelasticity, laplace transform, thermal stresses
Короткий адрес: https://sciup.org/146282824
IDR: 146282824 | DOI: 10.15593/perm.mech/2024.1.01
Текст научной статьи Memory dependent response in an infinitely long thermoelastic solid circular cylinder
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN
In this current decade, many researchers have started a new contribution on memory-based derivatives. In 2011, Wang and Li [1] gave the concept of MDD (memory-dependent derivatives) by surpassing the fractional derivative. Currently, MDD has developed as an emerging field of fractional calculus that is continually expanding due to its ability to reflect memory-dependent responses in various physical processes. Despite being specified on an interval, the fractional derivative (FD) mainly captures local change. The physical meaning of MDD is significantly more noticeable than that of FD. The MDD-dependent weight is reflected by the kernel function, while the time delay demonstrates the duration of the memory effect. Available research shows that the memory-related derivative is more appropriate for temporal modelling which is useful in describing the thermal effect of solid bodies. Memory-dependent derivatives are capable of replacing fractional derivatives and having useful applications in the field of thermoelasticity, thermoelectricity, particle physics and vibration mechanics etc. For more details on the fractional-related theory of thermal response, refer to the contents developed by many renowned researchers, as shown in references [2–13].
El-Karamany and Ezzat [14] constructed generalized thermoelastic theory with time delay and investigated MDD problem for a half space Cartesian body. Sun and Wang [15] reconstructed the memory dependent heat model based on the assumption that temperature increases slowly after heat transfer. Xue et al. [16] investigated thermal stresses in hollow cylinder containing internal and surface crack by using integral transform technique by considering heat conduction model with memory dependent derivatives. Ma and Gao [17] studied dynamic response of infinite hollow cylinder under thermal shock based on generalized nonlocal thermoelastic theory and MDD theory. Recently, Verma et al. [18] determined the impact of memory in hygrothermoelastic hollow cylinder by theory of uncoupled-coupled heat and moisture. Marin [19, 20] contributed the thermoelastodynamics study on bodies with void. Abouelregal et al. [21 to 26] elaborated the study of thermoelasticity based on higher-order memorydependent derivative with time delay and discussed vibrational behaviour in nanobeam. Atta [27] analyzed fractional operator response on thermal diffusion problem of infinite medium. Yu et al. [28] developed a novel thermoelastic model using memory-related derivatives and described its applications. Hussein [29] determined the solution by considering the circular cylinder problem under fractional theory.
Chepurnenko and Turina [30] determined the stressstrain relation for multilayer beams using the finite element method. Ogorodnikov et al. [31] constructed the mathematical model for nonlinear viscoelasticity and discussed the impact of fractional integro-differentiation. Also, various other authors contributed to the field and evaluated the impact of fractional responses on different bodies, as highlighted in [32–38].
According to the aforementioned literature review, the Memory dependent derivative surpasses the fractional derivative on the basis of significant improvements in memory-related response. Thus, the authors have the opportunity to investigate the impact of MDD in an infinitely long, solid circular cylinder whose lateral face is free from traction and exposed to a specified ambient temperature. To obtain the solution of temperature and stress distribution, Laplace transform is utilized and its inversion is carried out numerically by Fourier series expansion method as given by Honig and Hirdes [39]. Obtained thermoelastic responses are represented graphically and the effects of MDD are discussed.
1. Basic Equations
A memory-dependent derivative of function T ( x , t ) is described by Wang and Li [1] as a weighted integration of the common integer-order derivation on a slipping interval defined as
t
DmT( x, t ) = - K (t-^)T'( x, Е) d ^. (1)
to t-to
The m -th-order memory-dependent derivative of a function T ( x , t ) that is — times differentiable with respect to t is written as
D m T( x , t ) = —— D T( x , t ) = - K^t -^^-^ x -H d Е, (2)
to v , у t”-1 to v , to дЕ - ’ t-to where, Kernel function K (t — Е) and time delay to are chosen arbitrarily in order to capture materials real behaviors.
In general, 0 < K ( t — Е ) < 1 for ^e [ t — to , t ] and
|D to ¥ ( x , t )|<
dy ( x , t )
—d t
so that the magnitude of memory dependent derivative Dto f (x, t) is usually smaller than that d^( x, t)
of the common partial derivative —^---■
The kernels function may be chosen as
k (t-е)=1 - 2ь (t-9+a2 (t-у2= to to
1 - ( t -Е )
1 -II-s)
to f1 - t^i)
I to J
a = b = 0, a = 0, b = —,
a = 0, b = —,
a = b = 1,
where, a and b are constants.
2. Problem Formulation
Followed by Hussein [29], we assume a homogeneous, isotropic infinitely long solid circular cylinder having ( r , ψ , z ) as cylindrical polar coordinates and radius R . The cylinder's surface is considered to be traction-free. All the considered functions are dependent on r and time t as a result of the cylindrical symmetry.
Because of the radial symmetry of the problem, the u displacement elements are treated as u = ( u ( r , t ) ,0,0 ) .
The strain components produced due to displacement field are as
( λ+ 2 μ ) ∇ 2 e -γ∇ 2 T =ρ∂ 2 2 e .
where cubic dilatation erψ
|
∂ u err = , ∂ r |
(4) |
∂ t The constitutive relations giving the stresses |
σ ij have |
|
|
u e ψψ = r , |
(5) |
the form |
σ rr = 2 μ err +λ e -γ ( T - T 0), |
(13) |
|
- e = e = e = 0, ψ zrzzz , |
(6) |
σψψ = 2 μ e ψψ+λ e -γ ( T - T 0), |
(14) |
|
|
e is given by |
e zz =λ e -γ ( T - T 0), |
(15) |
||
|
∂ uu e =+ . ∂ rr |
(7) |
e = e = e = 0. z ψ rzr ψ . |
(16) |
|
Let's introduce the dimensionless variables:
Sherief et al. [13] presented the theory of fractional order of thermoelasticity, in which the heat conduction equation was presumed to be:
q + Td q = - k V T ; 0 < - < 1, (8)
d t where q denotes the element of the heat flux vector, τ represents the relaxation time, k denotes the thermal material conductivity and - is constant.
Yu et al. [28] recently provided an application of a memory-related derivative. In their study, they substituted the memory-dependent derivative (MDD) for fractional calculus to represent memory-dependence in the rate of heat flux in the Lord-Shulman generalised thermoelasticity theory, as follows:
q +τ D ω q =- k ∇ T . (9)
In absence of an inner thermal source, the heat transfer equation for isotropic materials has the following form:
(1 +τ D ω )( ρ C E ∂ T +γ T 0 ∂ e ) = k ∇ 2 T , (10)
∂t∂t where CE denotes the specific heat at static strain, ρ designates the density, T represents the temperature in absolute terms, and T0 is the temperature of the reference that is supposed to be such that T-T0 <<1.
The motion equation for this theory is formatted as
∂T∂
(λ+2μ)∇2u-γ =ρ ,(11)
∂r∂ where λ , μ denotes the Lame’s constants, and γ represents material constant specified by (3λ +2μ) αt where αt stands for the linear thermal expansion coefficient;
where the definition of ∇2 , the Laplace's operator in cylindrical polar coordinates, is v 2 1 d Г d
V =1 r— r dr I dr
We obtain below expression by using the divergence operator on both sides of equation (11) as r′=cηr,μ′=cηu,t′=c2ηt,
σ rr σ ψψ
τ′=cηt,σ′rr = , σ′ψψ = , rr μψψ μ
θ′= γ ( T - T 0), h ′= h , F ′= γ F , λ+ 2 μ k η c λ+ 2 μ
R ′= c η R ,
q r ′= γ q r , λ+ 2 μ k η c
where
λ+ 2 μ c =
ρ
η=ρ C E k
The governing equations (8), (9), (11) and (12) have the following forms when using the aforementioned non-dimensional variables and dropping the primes out of convenience
(1 +τ D ω )( ∂θ +ε ∂ e ) =∇ 2 θ , (17)
∂t∂t e = e = e = 0, zψrzrψ,
where е = TO Y о2 = (^ +2Ц)
( X+ 2 ц ) k n ’ ц ’
It is assumed that the initial conditions of the problem are of a homogeneous nature, complemented by the following limiting boundary conditions as:
-
(i) The surface of the cylinder is traction free
о rr ( r , t )| = 0 ; t > 0. (23)
r = R
-
(ii) The boundary condition for the heat convection
-
3. Problem-solving in the Integral Laplace Transform Domain
= H ( t ) . (24)
r=R d6 d r
Using the Laplace transform with relation-defined parameter s
^
T ( 5 ) _ j e - st T ( t ) dt . (25)
The following equations are obtained by applying the transform in equation (25) to both sides of equations (17) through (24).
and satisfying the two relations k1 + k2 = s (1 + e) (1 + G)+s2, k12k22 = s3 (1 + G).
The solution of Eq. (36) can be written in the form 6 = 6 1 + 9 2 where 9 i stands for complete integral of the equation
( V 2 - k ) 6 = 0 for i = 1,2. (37)
The result of the solution for equation (37) can be expressed as
6 = A( s)(k2- s2) Iо (kir)+ + Bi( s)(k2 - s2) K0 (kir) ; i = 1,2, where 10 (z), K0 (z) are the modified Bessel function forms of the first and second kinds, respectively, and Ai (s), Bi (s) , i = 1, 2 are parameters that rely only on s.
Thus the general solution of Eq. (36) is given by
-
6 = £ [ A ( s )( k i 2 - s 2) I о ( k r ) + B ( s )( k 2 - s 2) K о ( k r ) ] i = 1
since K 0 ( z ) not bounded at r = 0, we must putting B i ( s ) = 0 . Thus,
6 = £ A ( s )( k 2 - s 2) 1 0 ( k i r ) , (39)
i = 1
P 2 s 2 1 0 ( k 2 R ) - (2 k 1 / R ) 1 1 ( k 1 R ) (40)
f ( k 2 - s 2) k1 1 ( k 1 R ) [p 2 s21 о ( k 2 R ) - (2 k ,/ R ) 1 1 ( k 1 R ) ] 1 , s [- ( k 2 - s 2) k 2 1 1 ( k 2 R ) [ p2 s21 0 ( k R ) - (2 k ,/ R ) 1 1 ( k 1 R ) ]J
________________ P 2 s21 о ( k 1 R ) - (2 k 1 / R ) 1 1 ( k 1 R ) ________________ (41) | ( k 22 - s 2) k 2 1 1 ( k 2 R ) [p 2 s21 о ( k 1 R ) - (2 k 1 / R ) 1 1 ( k 1 R ) ] 1 , s [- ( k 2 - s 2) k 1 1 1 ( k 1 R ) [p 2 s21 о ( k 2 R ) - (2 k 2/ R ) 1 1 ( k 2 R ) ]J
Similarly, we get e = k2 A1(s) 10 (k1 r) + k22 A2(s) 10 (k2 r). (42)
G T j ( 1 - e - s “ ) f l - 2b- + 2a . )— f а 2 — 2 b + — 1 e " s “ I . (34) to | \ to s to 2 s 2 J ( to s J J
Eliminating e between (26) and (27), we get
{ V4 -V 2[ s ( 1 + e ) (1 + G ) + s 2] + s 3 (1 + G ) } 6 = 0. (35)
The equation (35) can be factorized as
( V 2 - k 1 2)( V 2 - k 22) 6 = 0, (36)
Using equation (42) as a substitute in (7) and integrating with regard to r gives us
u = k 1 [ A 1 ( s ) 1 1 ( k 1 r ) ] + k 2 [ A 2 ( s ) 1 1 ( k 2 r ) ] , (43)
d u
— = k 1 A 1 ( s ) d r
+ k 2 A 2( s )
I^r ) - k 1 1 o ( k 1 r ) +
1 1 ( k 2 r ) - k 2 I 0 ( k 2 r ) r
Substituting from equations (4), (5), (39)–(44) into (28) and (29), we obtain the stress components as and thermal heat transfer stress history is shown respectively in Fig. 4 to 8. In numerical computation non-dimensional relaxation time т = 0.1 and radius varies from r = 0 to r = R = 1.
2k 1
° rr = A 1 ( 5 ) P 5 1 0 ( k 1 r )-- 1 1 ( k 1 r ) +
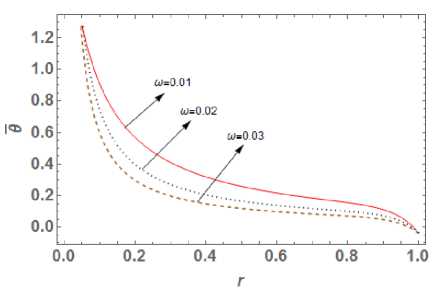
Fig. 1. Temperature distribution
+ A 2 ( 5 ) p 2 521 o ( k 2 r )-- 2-1 1 ( k 2 r ) ,
r
°vv = i A i ( 5 ) ( P 2 5 2 - 2 k i2 ) I о ( k 1 r ) + "у1 1 ( k 1 r ) [ +
1 r 1 (46)
+ L 2( 5 ) ( p 2 5 2 - 2 k 22 ) 1 0( k 2 r ) + 2 k 2 1 1 ( k 2 r ) I .
I r J
4. Numerical Inversion of the Laplace transformation
Solution of the problem is obtained in Laplace transform domain and its complex inversion is carried out numerically by assuming process assumed by Honig and Hirdes [39].
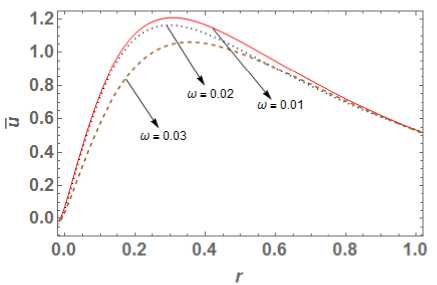
Fig. 2. Displacement distribution
The Laplace transform of y ( t ) is defined as
^
V ( 5 ) = j e~5t y ( t ) dt . (47)
Its numerical inversion is as given in [39] is utilized for calculation.
ct N e 1-/ v(t) = -t- 2v(c)+Re jn=1 H) v^c+— J ; (48) ct» 4.7. Fig. 3. Radial stress distribution
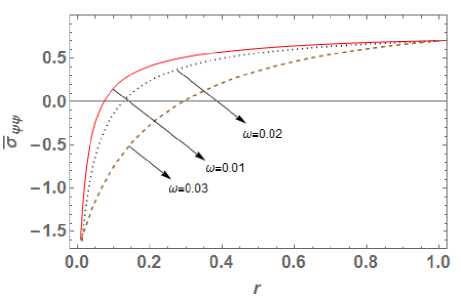
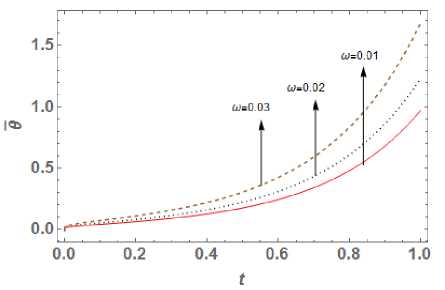
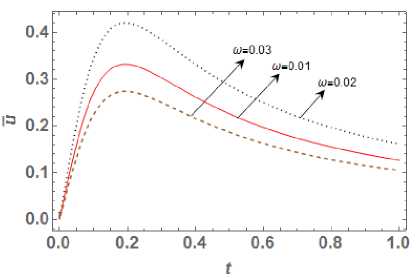
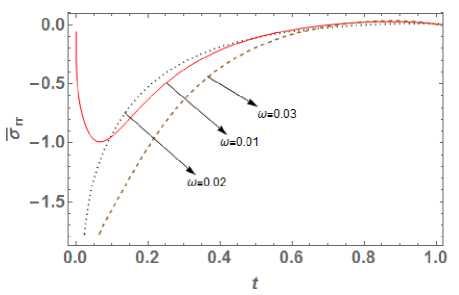
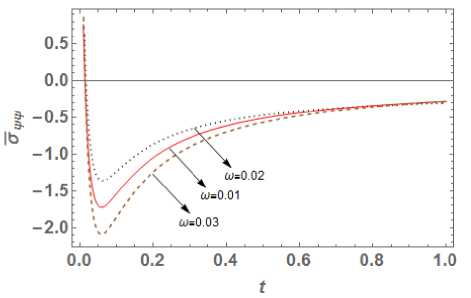
5. Numerical Results and Discussions Materials properties of copper metal mentioned in [29] are chosen for the purpose of numerical computation with the physical data: Symbol Value Unit p 8954 (kg)(m )-3 X 7.76 (10)10 (m । (5)-2 Ц 3.86 (10 )10 (m । (5)-2 n 8886.73 (kg)(m)-1 (K)-1 (5)- k 386 (kgm)(K "‘)(5 "3) T T0 293 ( k ) cE 383.1 (m2)(K-1)(5 ") Fig. 4. Hoop stress distribution In this part, our focus is to investigate the impact of time delay W= 0.01,0.02, 0.03 on temperature distribution, displacement distribution and thermal stresses, whose graphical plotting is as shown in Fig. 1 to 4 respectively. Also, time delay's effect on temperature history, displacement history Fig. 5. Effect on temperature history observed for larger time delay or we can say that temperature decreases with increase in value of parameter ю. The obtained result totally matches with [16] for Kernel function K (t — ^) = 1. Also temperature goes on decreasing towards outward radial direction for different value of time delay ю = 0.01, 0.02, 0.03 . Further we can say that thermal waves are varying continuously, smoothly and reach to steady state depending of time delay. Fig. 6. Effect on the displacement history Fig. 2 presents the variation of displacement distribution for different values of time delay ю along radial direction r . Displacement distribution is zero at r = 0 and reaches to its peak at r = 0.3 then it slight decreases towards outer radii. Here large distribution in displacement is noted for small values of parameter ю. Hence we can say that displacement is also significantly affected by values time delay parameter. Fig. 7. Effect on radial stress history Fig. 3 shows the radial stress distribution along radial direction with the impact of time delay parameters ю = 0.01, 0.02, 0.03 at t = 0.03 . The influence of time delay strongly affects the stress distribution and it is found that stresses decreases in the range 0 < r< 0.1 and then goes on increasing gradually towards outer radii. For higher value of parameter ю, large distribution in stress function is observed. Hence we can say a time delay dependent stress wave varies continuously and smoothly along radial direction. Also the value of radial stresses becomes zero at r = 1 which matches with the prescribed free-end mathematical condition as defined in equation (23). Fig. 4 shows the continuous and smooth variation of hope stress (ouu) distribution with impact of time delay in radial direction. The stress functions are compressive throughout the radial direction and large distributions in stresses are noted for small value of parameter ю. Further maximum stress distribution is obtained at r = 0.2 then after it gradually increases towards outer radii. Fig. 8. Effect on past hope stress The effect of time delay on temperature history at r = 0.5 is depicted in Fig. 5. Initially temperature is zero and goes on increasing with time for different value of ю . Also it is noticed that temperature varying smoother for large time dealy, hence we can say that effect of time delay on temperature history plays an important role which can be used in classification of materials on the basis of ability to conduct heat. Fig. 6 indicates that the displacement distribution is also significantly affected by different values of time parameter delay ю on temperature history. For large value of time delay small distribution in displacement history is observed for infinitely long circular cylinder. From Fig. 1 the great impact of time delay on the temperature distribution function is seen along radial direction at t = 0.03. The smoother distribution of temperature is The effects of the history of radial stress (arr) at r = 0.5 for time delay are depicted in Fig. 7. It is evident that with increase in time radial stresses gradually increasing towards outer radii and maximum distribution in stress is observed for small value of ю . It is noticeable that radial stresses are tensile in initial time period 0 < t < 0.2 and becomes compressive in range 0 < t < 0.2 . This indicates that radial stress history significant effected by the impact of time delay. Fig. 8 shows the impact of hoop stress (ow) history with impact of time delay r = 0.5 . Initially the stress (оии) decreases rapidly in the range 0 < t< 0.1 and gradually increases with increase in time. Also large variation in hoop stress distribution exists for higher value of parameter to. The finite speed of wave propogation is seen for different time delay parameter and obtained stress curve is compressive throughout the variation. Conclusion MDD is the extension part of FD theory. Fractional order theory reflects the memory effect which is given by Caputo fractional derivative and applicable to wave equation and diffusion equation. While MDD is the timeframe reflects the duration of the memory effect and the kernel feature reflects the dependent weight. The heat flow solution is obtained employing the fractional order theory as a long tail solution that corresponds to the kernel. In this paper we modify the work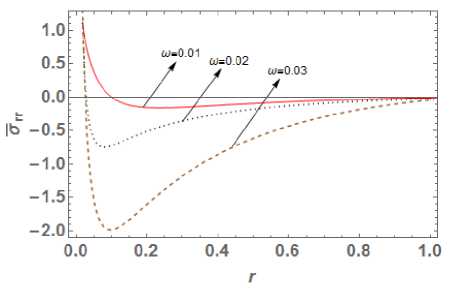
Список литературы Memory dependent response in an infinitely long thermoelastic solid circular cylinder
- Wang J.L., Li H.F. Surpassing the fractional derivative: Concept of the memory-dependent derivative. Computers and Mathematics with Applications. 2011,Vol. 62. pp. 1562–1567
- Oldham K.B., Spanier J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Mathematics in Science and Engineering, Academic Press, New York. 1974.
- Miller K.S. Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. A Wiley- Interscience Publication, JohnWiley Sons, New York.1993.
- Podlubny I. Fractional Differential Equations. Mathematics in Science and Engineering, Academic Press,San Diego, Calif. 1999.
- Samko S.G., Kilbas A.A., Marichev O.I. Fractional Integrals and Derivative: Theory and Applications. Gordon Breach Science Publishers, New York. 1993.
- Kilbas A.A., Srivastava H.M., Trujillo J.J., Theory and Applications of the Fractional Differential Equations. Elsevier (North-Holland), Math. Studies,2006, Vol. 204.
- Caputo M., Mainardi F. A New Dissipation Model Based on Memory Mechanism. Pure and Applied Geophysics. 1971, Vol. 91, pp. 134–147.
- Caputo M., Mainardi F. Linear Model of Dissipation in Anelastic Solids. Rivis ta del Nuovo cimento, 1971, Vol. 1, pp.161–198.
- Caputo M. Vibrations on an Infinite Viscoelastic Layer with a DissipativeMemory. Journal of the Acoustical Society of America. 1974, Vol. 56, pp. 897–904.
- Youssef H. M. Al-Lehaibi E.A.. Fractional Order Generalized Thermoelastic Half-space Subjected to Ramp-type Heating. Mechanics Research Communications. 2010, Vol. 37, pp. 448–452.
- Povstenko Y.Z. Fractional Radial Heat Conduction in an Infinite Medium with a Cylindrical Cavity and Associated Thermal Stresses. Mechanics Research Communications. 2010, Vol. 37, pp. 436–440.
- Povstenko Y.Z. Fractional Heat Conduction Equation and Associated Thermal Stress. J. Therm. Stresses, 2005, Vol. 28, pp. 83–102.
- Sherief H.H., El-Sayed A. M. A., Abd El-Latief A. M. Fractional Order Theory of Thermoelasticity. International Journal of Solids and Structures. 2010, Vol. 47(2), pp. 269–275.
- El-Karamany A. S., Ezzat M. A. Modified Fourier's Law with Time-Delay and Kernel Function: Application in Thermoelasticity. Journal of Thermal Stresses. 2015, Vol.38(7), pp. 811-834.
- Sun W.W., Wang J.L. Reconstruct the Heat Conduction Model with Memory Dependent Derivative. Applied Mathematics. 2018, Vol. 9, pp. 1072-1080.
- Xue Z.N., Chen Z.T., Tian X.G. Transient thermal stress analysis for a circumferentially cracked hollow cylinder based on memory-dependent heat conduction model. Theoretical and Applied Fracture Mechanics. 2018, Vol. 96, pp.123–133.
- Ma Y., Gao Y. Dynamic response of a hollow cylinder subjected to thermal shock considering scale effect and memory dependent effect. Mechanics of Advanced Materials and Structures, 2021 doi: 10.1080/15376494.2021.1931732
- Verma J., Lamba N.K., Deshmukh K.C. Memory impact of hygrothermal effect in a hollow cylinder by theory of uncoupledcoupled heat and moisture. Multidiscipline Modeling in Materials and Structures, 2022, Vol. 18(5), pp. 826-844.
- Marin M. Contributions on uniqueness in thermoelastodynamics on bodies with voids. Ciencias matematicas (Havana). 1998, Vol. 16(2), pp. 101-109.
- Marin M. A temporally evolutionary equation in elasticity of micropolar bodies with voids. U.P.B. Sci. Bull., Series A-Applied Mathematics Physics. 1998, Vol. 60(3-4), pp. 3-12.
- Abouelregal A. E., Moustapha M. V., Nofal T. A., Rashid S., Ahmad H. Generalized thermoelasticity based on higherorder memory-dependent derivative with time delay. Results in Physics. 2021, Vol. 20, 103705.
- Abouelregal A. E., Sedighi H. M., Faghidian S. A., Shirazi A. H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Universitatis. 2021, Vol. 19(4), pp. 633-656.
- Abouelregal A.E., Atta D., Sedighi H.M. Vibrational behavior of thermoelastic rotating nanobeams with variable thermal properties based on memory-dependent derivative of heat conduction model. Arch. Appl. Mech.. 2023, Vol. 93, pp. 197–220.
- Abouelregal A.E., Askar S.S., Marin M., Badahiould M. The theory of thermoelasticity with a memory-dependent dynamic response for a thermo-piezoelectric functionally graded rotating rod. Sci Rep., 2023, Vol. 13, 9052.
- Abouelregal A.E. Fractional Order Generalized Thermopiezoelectric Semi-infinite Medium with Temperaturedependent Properties Subjected to a Ramp-type Heating. Journal of Thermal Stresses. 2011, Vol. 11, pp. 1139–1155.
- Abouelregal A.E. Fractional heat conduction equation for an infinitely generalized thermoelastic long solid cylinder. International Journal for Computational Methods in Engineering Science and Mechanics. 2016, Vol. 17(5), pp. 374-381.
- Atta D. Thermal Diffusion Responses in an Infinite Medium with a Spherical Cavity using the Atangana-Baleanu Fractional Operator. Journal of Applied and Computational Mechanics.2022, Vol. 8(4), pp. 1358-1369.
- Yu Y.J., Hu W., Tian X.G. A Novel Generalized Thermoelasticity Model Based on Memory-Dependent Derivative. Int. J. Eng. Sci. 2014, Vol. 811, pp. 123–134.
- Hussein E.M. Fractional Order Thermoelastic Problem for an Infinitely Long Solid Circular Cylinder. Journal of Thermal Stresses. 2015, Vol. 38(2), pp. 133-145.
- Chepurnenko A.S., Turina V.S. Application of the finite element method in combination with the contact layer method to determine the stress-strain state of multilayer beams. PNRPU mechanics bulletin. 2023, Vol. 4, pp. 130-139.
- Ogorodnikov E.N., Radchenko V.P., Ungarova L.G. Mathematical models of nonlinear viscoelasticity with operators of fractional integro-differentiation. PNRPU mechanics bulletin. 2018, Vol. 2, pp. 147-161.
- Kumar N., Kamdi D. B. Thermal behavior of a finite hollow cylinder in context of fractional Thermoelasticity with convection boundary conditions. Journal of Thermal Stresses. 2020, Vol. 43(9), pp. 1189-1204.
- Lamba N.K., Deshmukh K.C. Hygrothermoelastic response of a finite solid circular cylinder. Multidiscipline Modeling in Materials and Structures. 2020, Vol-16(1), pp. 37–52.
- Kumar R., Kumar N. Analysis of Nano-Scale Beam by Eigenvalue Approach in Modified Couple Stress Theory with Thermoelastic Diffusion. Southeast Asian Bulletin of Mathematics. 2020, Vol. 44, pp. 515–532.
- Lamba N.K. Thermosensitive response of a functionally graded cylinder with fractional order derivative. Int. J. of Applied Mechanics and Engineering. 2022. Vol. 27(1), pp.107-124.
- Lamba N.K., Deshmukh K.C. Hygrothermoelastic response of a finite hollow circular cylinder. Waves in Random and Complex Media. 2022, doi: 10.1080/17455030.2022.2030501
- Lamba N.K. Impact of Memory-dependent Response of a Thermoelastic Thick Solid Cylinder. Journal of Applied and Computational Mechanics. 2023, Vol. 9(4), pp.1135-1143.
- Lamba N.K.,Verma J., Deshmukh K.C. A Brief Note on Space Time Fractional Order Thermoelastic Response in a Layer. Applications and Applied Mathematics: An International Journal. 2023, Vol. 18(1), Article 18.
- Honig G., Hirdes U. A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Mathe.1984, Vol. 10(1), pp. 113–132.


