Мера упорядоченности размещения геологических, минералогических и надмолекулярных объектов в пространстве

В минералогии, петрографии, литологии, палеонтологии, металлогении и других отраслях наук о Земле давно обсуждается задача измерения степени упорядоченности в размещении точек, под которыми понимаются центры минеральных зерен, ру-допроявлений, геохимических аномалий, других геологических тел, глобул и надмолекулярных структур. Широко известны работы [3, 4], в которых распределение числа точек по одинаковым ячейкам сравнивается с распределением Пуассона и делается вывод об их случайном, с тенденцией к группировке или к регулярности размещении. Однако меру упорядоченности этот метод вычислить не позволяет. Кроме того, вывод о случайном или ином распределении по ячейкам действителен только для выбранного размера ячеек.

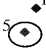
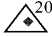
Другой подход основан на изучении расстояний между точками [6, 5]. Для этой цели используется распределение расстояний между ближайшими точками, а также расстояний до второй, третьей, ... n -й по дальности точки. Исследования проводились в пространствах различной размерности (от 2 до 20 [5]). 20

Известны обширные исследования распределения расстояний n -го порядка дальности в трехмерном пространстве для измерения степени упорядоченности глобул в шунгитах, антраксолитах, опалах [1, 2].

Введем (и уточним) основные понятия, относящие к данной проблеме. Ближайшее расстояние — расстояние до ближайшей точки; n - ближайшая точка — точка, находящаяся на n -м месте в ранжированном ряду расстояний от рассматриваемой точки; R ( X i X j ) — ранг, или порядок дальности точки X j от точки X i ; R ( X i X j ) — порядок дальности точки X i от точки X j . В общем случае эти ранги не совпадают. Но если R ( X i X j ) = R ( X j X i ), то точки называются взаимно ближайшими , или симметричными , например n - симметричными , если n — порядок близости этих точек. Определение симметричных точек как точек, для которых R ( X i X j ) = R ( X j X i ), необходимо и достаточно. Кроме того, оно конструктивно и позволяет по результатам ранжирования расстояний легко составить списки n -симметричных точек. Именно так трактуется понятие симметричности точек в фундаментальной монографии

Миллера и Кана, хорошо известной в русском переводе: «Если X 0 — ближайшая точка к X 1 , а X 1 — ближайшая точка к X ₀, то они симметричны друг другу» [4, стр. 386].

Как видим, никаких дополнительных условий, кроме взаимной близости, авторы не ставят. Далее они обобщают понятие симметричности на n -ближайшие точки: «Допустим, что точки, окружающие X ₀, рассматриваются в порядке их близости. Если X 1 — ближайшая точка к X ₀, то следующая ближайшая точка будет X , , третья — X 3 и т. д. Понятие симметрии в расположении точек теперь можно распространить на ближайшую точку с номером n . Это означает, что если X_n — ближайшая точка к X ₀, то согласно определению X_n будет ближе к точке X ₀, чем ко всем другим точкам, за исключением точек X 1 , X , ,... X _п-1, которые образуют последовательность ближайших к X ₀ точек, упорядоченную по величине близости» [4]. И здесь при определении понятия n -симметричных точек не вводится никаких дополнительных условий.

Для более глубокого анализа n -симметричности обратимся к

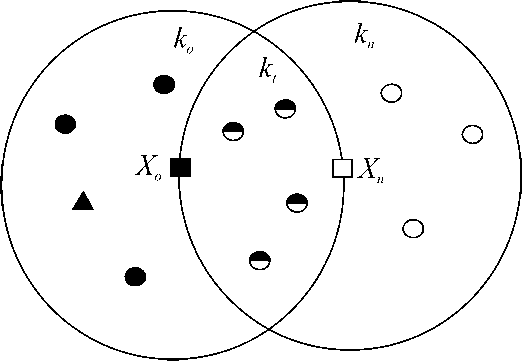
Рис. 1. Расположение n -симметричных точек X 0 и X_n (квадратики) на плоскости при n = 8. Пустые кружки — точки, не входящие в множество n -ближайших к точке X , ; залитые кружки — точки, не входящие в множество n-ближайших к точке X_n , наполовину залитые — входящие в оба множества. «Качество» изображенной n -симметричности равно 4/(n — 1) = 4/7 = 0.57. Залитый треугольник — точка, нарушающая равенство k ₀ = k_n и, соответственно, n -симметричность. По Е. А. Голубеву [1, 2], точки X । и X n являются лишь 5-симметричными

Однако Е. А. Голубев [1, 2 и др.] теоретические значения вероятностей n -симметричных точек заимствует из таблицы Миллера и Кана [4], где они, как мы показали выше, трактуются по -другому. Таким образом, метод n -симметричных точек у Е. А. Голубева находится в противоречии с принятой в [4] и [8] трактовкой n -симметричных точек и дает, по всей видимости, сомнительные результаты.

Миллер и Кан в [4] указывают, что вычисленные Кларком [7, 8, 9] теоретические вероятности n -симметричных точек относятся к слу-

чайному размещению точек в неограниченном пространстве . По авторской компьютерной программе мы многократно моделировали случайное размещение точек в единичном квадрате, единичном кубе и единичных гиперкубах размерностью до 20 и

рис. 1. На нем квадратными значками изображены n -симметричные точки порядка 8, т. е. при n = 8. Очевидно, что для точки X , порядок близости n равен n = k ₀ + k_t + + 1 = 8 и для точки X_n он равен n = k_n + + k_t + 1 = 8, что и должно быть по условию симметричности, где k_n — число точек в сегменте круга с центром X_n , k ₀ — число точек в сегменте круга с центром X , , k_t — число точек в общем сегменте. Очевидно, что n -симметричность обеспечивается исключительно равенством k ₀ = k_n , т. е. равенством числа точек в пределах сегментов кругов радиуса r без общей (пересекающейся) их части, в которой имеется k_t точек.

Отсюда следуют два интересных вывода: 1) можно ввести полезное понятие « находиться между точками X и X_n » и отнести к этому множеству точки k_t ; 2) можно охарактеризовать качество n-симметричности . Наилучшим оно будет, когда k ₀ = k_n = 0, т. е. когда n -симметричность порождена только k_t точками при k_t = n — 1, т. е. находящимися между точками X ₀ и X_n . Наихудшим — когда оно порождено точками k ₀ = k_n * 0 при k_t = 0. Итак, качество n -симметричности можно охарактеризовать величиной S , S = k_t /( n — 1), где n — порядок близости, S = (0..1).

ся от 1 до N , то n -я ближайшая точка будет являться n -симметричной при выполнении условия: расстояние ( X 0 , X n ) <  расстояния ( X_n , X i ) для всех i , удовлетворяющих n <  i <  N » ([1, стр. 38], выделено Е. А. Голубевым). Сопоставляя это утверждение с рисунком, устанавливаем, что оно эквивалентно требованию отсутствия точек k ₀ = k_n . Это приводит к значительному занижению числа n -симметричных точек по сравнению с вычисленными Кларком [6, 7, 8] и в монографии Миллера и Кана. По-существу, в работах [1,2] симметричными точками признаются только такие, симметричность которых обусловлена k_t -точками, т. е. точками,

располагающимися между точками

^X 0 и ^X n .

y

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

сло точек совокупности, и n меняет-

получили хорошее согласие с приведенными [4] теоретическими данными, за исключением больших n , приближающихся к общему числу точек. Причина выяснилась после идентификации пар n -симметричных точек: они располагались близ противоположных вершин гиперкубов. Число таких пар мало, поэтому доля симметричных среди них велика. Будь точки в самих вершинах, они все были бы n -симметричными (см. рис. 2, таблицу). В таблице представлены сравнительные данные вероятностей появления n -симметричных точек: 1) в двухмерном неограниченном пространстве по Кларку [7], 2) установленные нами с помощью компью-

терного моделирования в единич-

ном гиперкубе и 3) рассчитанные для

0.0

0.0     0.1     0.2     0.3     0.4     0.5     0.6    0.7     0.8     0.9      ^1.0 x

Рис. 2. Случайное размещение точек (ромбики) и расположение среди них 18- и 19-симметричных (точки одинаковой обводки). Наблюдается их концентрация близ

углов квадрата

Теоретические, модельные и эмпирические частоты появления n -симметричных точек в двухмерном пространстве

Вероятность появления n-симметричных точек Порядок близости n 1 2 9 10 Из таблицы [4], рассчитанные Кларком [8] 0.6215 0.3863 0.0138 0.0086 При моделировании случайного размещения 500 точек в единичном квадрате 0.5880 0.3160 0.0960 0.1320 В совокупности 575 центров темноцветных зёрен в квадратной плитке керамогранита 0.6504 0.3026 0.1252 0.1321 В совокупности 747 вершин Приполярного Урала в пределах выделенного квадратного участка карты 0.5783 0.2758 0.1285 0.0964 двух природных объектов. При удовлетворительном сходстве частот 1- и 2-симметричных точек с теоретическими частотами по Кларку [8] мы наблюдаем при n = 9,10 превышение эмпирических и модельных частот над кларковыми более чем на порядок. На этих примерах легко убедиться в том, как велико влияние краевого эффекта на вероятность появления n-симметричных точек, располагающихся вблизи границ контуров размещения точек. Е. А. Голубев [1,2] столкнулся с этой же проблемой краевого эффекта и ошибочно указал, что избежал его, рассматривая только оконтуренную им центральную часть исследуемых под микроскопом площадок, но не указал формулу расчета числа n-симметричных точек. Как оказалось, простое оконтуривание не позволяет решить проблему края. Краевая проблема — это тот случай, когда оценку теоретического распределения можно решить, многократно моделируя размещение точек в конкретном изучаемом контуре.

Специальный интерес представляет случай, когда точки являются центрами физических тел — минералов, глобул — имеющих конечные размеры. Если соседние частицы почти все касаются друг друга, то образуется плотная структура, в которой распределение ближайших расстояний не соответствует концепции Кларка [7].

Нами проведена серия моделирований почти регулярного размещения точек. Для этого сначала размечалась регулярная (квадратная) сеть точек, затем каждая точка отклонялась от узла регулярной сети в произвольном направлении на небольшое случайное расстояние, задаваемое средним квадратическим отклонением. Ожидалось, что вероятность появления 1-симметричных точек будет значительно выше, чем для случайного распределения. Отношение частоты 1-симметричных точек к теоретическому значению частоты при случайном распределении могло бы в этом случае служить мерой ближ- 22

него порядка. Увы, это не подтвердилось. Зато вероятности n -симметричных точек сильно выросли при больших значениях n (рис. 4, 5).

Для объяснения этого явления обратимся к некоторым свойствам регулярных и квазирегулярных размещений точек. В регулярных сетях каждая точка окружена правильными оболочками других точек. Для нас интерес представляют ближайшие оболочки. В двухмерном пространстве самая простая сеть — это сеть равносторонних треугольников. Каждая

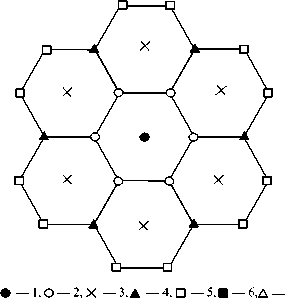
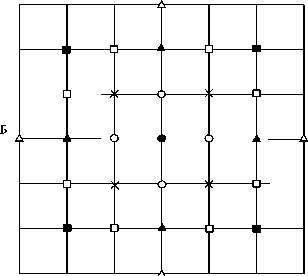
Рис. 3. Оболочки при квазирегулярном размещении точек: А — треугольная сеть, Б — квадратная сеть. 1 — центральная точка, относительно которой рассматривается размещение точек удаляющихся оболочек; 2—7 — оболочки: 2 — ближайшая, 3 — вторая, 4 — третья, 5 — четвертая, 6 — пятая, 7 — шестая

012345678910 ⁿ

Рис. 4. Частости и вероятности (P, ось ординат) n -симметричныхточек (ось абсцисс). Залитые кружки — теоретические вероятности по Кларку [3], крестики — частости по 500 случайно распределенным в пределах единичного квадрата точкам, пустые кружки — экспериментальные частости среди 575 темноцветных зерен в пределах квадратной площадки плитки керамогранита, треугольники — экспериментальные частости по 747 точкам — вершинам Приполярного Урала в пределах выбранного квадратного участка карты

точка в ней окружена шестью ближайшими точками. Это значение есть первое координационное число (рис. 3, А). Вторая оболочка (крестики) образует больший шестиугольник. Второе координационное число в ней также равно шести. Третья оболочка (залитые треугольники) также содержит шесть точек. Четвертая оболочка (не-залитые квадратики) содержит 12 точек. На рис. 3, Б изображены оболочки для квадратной сети.

Теперь представим себе, что в каждой оболочке каждая точка немного

Рис. 5. Частости и вероятности (Р, ось ординат) «-симметричных точек (ось абсцисс) порезультатамихмоделированияпочтипоквадратнойсетисотклонениямиотнеё, задаваемыми средним квадратическим отклонением о в долях от размера ячейки сети. Залитые кружки — теоретическая кривая по Кларку [4], остальные обозначения точек относятся к модельным данным с обозначением значений о у линий

смещена от своего «правильного» положения, оставаясь в пределах своей оболочки. Это означает, что расстояния всех точек этой оболочки до центральной точки меньше, чем расстояние самой близкой точки следующей оболочки, и больше, чем расстояние самой удаленной от «центра» точки предыдущей оболочки. Пока сохраняется это условие, т. е.

k k + 1

max(r ) < min(ri )и min( riik) > max( riik 1), (1) где rik — расстояние i-той точки от «центра» k-той оболочки, размещение будем называть квазирегуляр-ным. При квазирегулярном размещении точки не теряют своей принадлежности к «своим» оболочкам. Квазирегулярное размещение моделируется путем случайных отклонений точек от их регулярных положений с последующим цензурированием и исключением отклонений, нарушающих неравенства (1). Для дальних оболочек неравенства будут нарушаться ввиду суммирования случайных отклонений, но вероятность их будет невелика.

Для квазирегулярных размещений точек очевидны следующие утверждения: 1) n -ближайшие точки, ранжированные по расстояниям, будут располагаться группами по K i точек, где K i — координационное число в i -той оболочке; 2) вероятность появления n -симметричных точек P одинакова для каждой группы и определяется неравенством:

P i

> Ki ’

так как отклонение «центральной» точки от регулярного положения в некотором направлении увеличивает вероятность того, что точки, расположенные близ этого направления, в i-той оболочке будут n-симметричными с «центральной».

Конкретные вероятности n -симметричных точек зависят как от координационного числа в этой оболочке, так и от функции распределения погрешностей (абсолютного значения отклонения точек от их регулярных положений). Они могут быть определены компьютерным моделированием и служить диагностическим критерием квазирегулярного размещения и эмпирической оценки координационных чисел в оболочках.

Данные предварительного моделирования квазирегулярных размещений (всего по 100 точек на эксперимент) приведены на рис. 5. Поражает огромное превышение вероятностей n -симметричных точек как над теоретическими при больших n (нижняя гладкая кривая), так и над эмпирическими и модельными, в которых учтен краевой эффект (см. пучок верхних кривых на рис. 4). Это превышение настолько существенно, что не может получить разумного объяснения в рамках рассматриваемой модели: ведь отклонения точек от их регулярных положений в данной модели не транслируются на дальние оболочки . Не выявлено также отклонений вероятностей n -симметричных точек при n = 1 и n = 2 от теоретических значений для случайного распределения, что можно объяснить малой повторяемостью модельного эксперимента.

Таким образом, вопрос об эффективности метода n-симметричных точек в качестве меры упоря доченности их размещения в пространстве остается дискуссионным. Во-первых, исключение краевого эффекта требует отказа от базы для сравнения с «теоретическими» вероятностями Кларка, вычисленными для неограниченного пространства, и замены этой базы с моделированными вероятностями в контуре, идентичном изучаемому природному случаю, а это представляет определенные трудности.

Во-вторых, навести «переходный мостик» между размещениями точек с большим влиянием случайных факторов и почти кристаллографическим квазирегулярным пока не удается, хотя предварительные компьютерные эксперименты обнадеживают.

В-третьих, меру упорядоченности размещения частиц, слагающих плотные или пористые материалы (горные породы, осадки, сыпучие материалы, руды в процессе их обработки и обогащения), следует искать, вероятно, в основе метрики Ю. Л. Войтеховского, в которой расстояние между частицами измеряется числом переходов от одного зерна к другому.