Мера упорядоченности социально-экономической системы для оценки её эффективности

Введение . Управление экономической системой всегда основано на критериях оценки её эффективности. Традиционно используются такие критерии эффективности, как валовой внутренний продукт, валовой региональный продукт, затраты – выпуск, валовая прибыль, рентабельность, производительность труда и др. Каждый из них имеет свои преимущества. Их общая черта – характеристика эффективности управления в данный момент или ретроспективе, возможен и прогноз эффективности функционирования системы в будущем на основе ретроспективных данных. Однако эти критерии не дают обобщающей оценки эффективности управления экономической системой с точки зрения влияния на её упорядоченность, способность в будущем устойчиво функционировать за счёт инерции экономической системы. Управление экономической системой по указанным критериям позволяет получить высокую эффективность в данный момент времени, но при этом исчерпать ресурс устойчивости, упорядоченности системы и, как результат, в будущем получить кризисные явления.

Как показали предыдущие исследования автора статьи (Курочкин, 2017), имеет перспективу разработка методов и критериев оценки эффективности систем управления «по результатам», с точки зрения стабильности развития экономических систем (холдинга, корпорации, кластера, региона, государства в целом). Востребована разработка обобщающего критерия оценки её эффективности, дающего информацию о состоянии её структуры, упорядоченности. Основу такого обобщающего критерия может составить относительно новый подход к исследованию экономических систем, основанный на использовании меры упорядоченности системы (Дятлов, 2012; Чепьюк, 2016; Коровникова, 2017). Актуальным является вопрос обоснования критерия оценки эффективности управления экономической системой на базе меры его упорядоченности, устойчивости функционирования.

Гипотеза нашего исследования состояла в том, что предполагалось возможным обоснование критерия оценки эффективности экономической системы на базе энтропийного подхода к экономике.

С целью доказательства сформулированной нами гипотезы исследовали возможность использования в качестве критерия эффективности экономической системы мера упорядоченности сложных систем, как открытых, так и закрытых – энтропию.

Материалы и методы . Для математического описания функционирования системы в данной работе мы использовали естественно-физический подход, так как взаимосвязи имеют физическую природу и количественно измеримы.

В методологическую основу исследований была положена математическая теория энтропии. Результаты, которые в рассматриваемом аспекте получили исследователи К. Шеннон, Н. Мартин, Дж. Ингленд, А.Н. Колмогоров, А.Я. Хинчин, И.М. Гельфанд и их последователи разработки в области теоретической физики Р. Клаузиуса, W. Nerst, М. Планка, J.W. Gibbs и др. (Ландау, Лифшиц,1976) исходили из того, что Н. Мартин и Дж. Ингленд (Мартин, Ингленд, 1998) установили следующее:

• –    рассматривая пространство (Ω , F , Ρ ) – это пространство Лебега, определили некоторое событие E ∈ F как математическую модель некоторого случайного события;

• –    определив на множестве событий в упомянутом пространстве функцию I (E ), как количественную меру информации, установили понятие информации как вещественную функцию событий, зависящую только от вероятности событий;

• –    допуская, что ξ – счётное измеримое разбиение пространства (Ω, F , Ρ ), а I (ξ) – информационная функция разбиения ξ, заданная на Ω, значение которой для любого исхода равно количеству информации, получаемой при реализации содержимого ω элемента А разбиения ξ , можно определить I (ξ)(ω)», как (Мартин, Инглен, 1998: 54):

I (9(<у) = -Ы I_A  logP (A),                              (1)

A = 5

где   I a - характеристическая функция (индикатор) множества А ;

I (5) - функция на фактор пространстве (Q 5 , F 5 , Р 5 ).

При этих условиях энтропией счётного измеримого разбиения ξ пространства Лебега (Ω, F , Ρ ) называется математическое ожидание информационной функции разбиения. Энтропия разбиения обозначается H(X) и составляет выражение (1), то есть энтропия счётного разбиения – это среднее количество информации, заключённой в отвечающем разбиению системе (Мартин, Инглен, 1998). Данное определение энтропии весьма важно для разработки математической модели рассматриваемой системы, состоящей из элементов, которые соединены функциональными связями, которая в процессе эволюции переходит из одного состояния в другое в пространстве состояний, которое можно представить в виде счётного множества состояний I (ξ) ∈ (Ω, F , Ρ ), при этом (приведём без доказательства, которое изложили Н. Мартин и Дж. Ингленд в своей монографии (Мартин, Ингленд, 1988)): п            п

• -bT.pt log2pt< -ЬТ pt 109241 =-b’L^iCtlog22-Nl/B(2)

l = 1l=1

Причём равенство (1), которое можно записать в виде (Мартин, Инглен, 1998: 91):

МН < E(N)+log B(3)

достигается тогда и только тогда, когда p i =q i при всех i.

Формула К. Шеннона, которая связывает информацию и энтропию, имеет следующий вид1:

H = - b S p l log 2 p l(4)

Для методики наших исследований значимым является принятие методического положения о том, что существует установленная академиком В.А. Трапезниковым связь между эффектом от функционирования экономической системы и количеством информации, которая интерпретируется выражением (Трапезников, 1983):

E = E max (1 - E -l/ 10) ,                                  (5)

где E max – эффект идеально функционирующей системы.

В исследованиях учтены современные работы В.В. Виноградовой и А.А. Краснова по изучению изменений энтропии экономической системы в зависимости от распределения ресурсов по элементам системы (Краснов, 2009: 167–172). Методика исследований также основана на результатах исследований, выполненных в МГТУ им. Н.Э. Баумана и УрФУ.

Степень разработанности темы . Исследователи экономических систем отмечают системный кризис современной либерально-рыночной экономики, периодически случающиеся финансовые и экономические кризисы, который являются следствием того, что экономические системы программируются и воспроизводятся по правилам управляемого хаоса (Солодовников, 2018). Переход к управлению развитием экономической системы на базе контроля меры упорядоченности и хаотичности позволит решить базовые вопросы неопределённости экономических явлений и процессов (Дятлов, 2012; Коровникова, 2017). Подобное утверждение относится, прежде всего, к повышению устойчивости экономических систем. Данное понятие сформировалось в прошлом веке (Кондратьев, Ляпунов) и отражает такое свойство системы, как способность возвращаться в состояние равновесия в том случае, когда она будет выведена из него под воздействием внешних или внутренних факторов. Как известно, экономические системы относятся к классу активных нечётких систем, которые характеризуются сложностью, открытостью и неопределенностью (Бурков, 2009), в связи с чем они должны идентифицироваться иерархическими нечеткими структурами, «которые можно интерпретировать как состояния системы и субъективные вероятности этих состояний». Одной из основных макроскопических характеристик состояния системы является энтропия (Федотов, Новожилова, 2011). Указанные авторы предложили воспользоваться относительно энтропии H(A) , негэнтропии H(-A), как меры упорядоченности, аксиомами (De Luca, Termini, 1972):

• 1)    H(A) = 0 тогда и только тогда, когда А – обычное множество;

• 2)    H(A) = max тогда и только тогда, когда все р А(xi ) = 0,5, i =1,^, n ;

• 3)    H(A) = H(-A) - симметрия относительно точки перехода р А = 0,5.

«В зависимости от той или иной эмпирической меры, можно обосновать принцип существования энтропии и предложить различные виды энтропий состояния сложной системы. Энтропия является характеристической функцией пространства состояний системы… Для различных состояний сложных систем между статистической энтропией и информационными энтропиями в представлениях Хартли и Шеннона существуют тесные связи, которые указывают на сходство данных величин между собой (Аверин, Звягинцева, 2016).

Следовательно, энтропия, как мера хаоса, может быть рассмотрена в качестве меры упорядоченности экономической системы.

Результаты и обсуждения . Рассмотрим понятие энтропии. Отметим, что данное фундаментальное понятие физики было впервые введено в научный обиход немецким учёным Р. Клаузиусом, сформулировавшим позднее второе начало термодинамики (энтропия системы стремится к максимуму). Иными словами: Р. Клаузиус определил возможные варианты направления эволюции как меры рассеивания энергии. Его заслуга заключается, наряду с другими научными достижениями, в формировании новой функции состояния физической системы, которую он назвал энтропией. Рассматривая замкнутые термодинамические системы, Р. Клаузиус для случая необратимого процесса доказал неравенство, впоследствии получившее его имя. Кроме того, позднее Р. Клаузиусом, В. Томпсоном и последователями (Ландау, Лифшиц, 1976: 44–49) их научной школы было аргументировано: энтропия может выступать как мера все более возрастающей неупорядоченности «набора случайностей» частей системы, приводящая к «тепловой смерти» Вселенной, что следует из того, что «какие бы изменения в реальных изолированных системах ни происходили, они всегда ведут к увеличению энтропии». Данное выражение, известное как второе начало термодинамики, подвергал сомнению Л. Больцман (Ландау, Лифшиц, 1976: 130–132), который показал применимость данного начала только для статистических, замкнутых систем, который установил взаимосвязь между термодинамической вероятностью состояния системы Р nd и энтропией H (X) , а также доказал, что «возрастание энтропии статистических систем указывает лишь наиболее вероятное протекание процессов». Впоследствии М. Планк математически уточнил открытую Л. Больцманом закономерность и привёл её к виду:

H (X) = k lnР nd                                              (6)

где k – постоянная Больцмана, k = 1,38*10 ^–23.

Рассматривая статистические макроскопические системы при изменениях температуры, В. Нерст (Ландау, Лифшиц, 1976: 86–87) заметил, что с её понижением упорядоченность системы растёт, сначала газ превращается в жидкость, а затем переходит в твёрдую фазу, которые более упорядочены, чем газ. Из этого рассуждения В. Нерст сформулировал третий закон термодинамики о том, что «с приближением абсолютной температуры к нолю энтропия также стремится к нолю». Впоследствии теория энтропии была обобщена для более широкого класса систем: организационные, социальные, экономические. В социальных науках в XIX в. понятие энтропии использовалось для измерения культурного и нравственного декаданса общества, в частности, было введено понятие « энергия эволюции системы», которое характеризовало способность социально-экономической системы выполнять полезную работу, направленную на трансформацию своей структуры в качественном и количественном измерении. Впервые идею об эволюции по отношению к биологическим системам сформулировал Ж-Б. Ламарк. Он считал, что эволюционные изменения детерминированы систематическим приобретением новых свойств и качеств. Позднее идея Ламарка была несколько иначе интерпретирована Ч. Дарвиным и А. Уоллесом. В наше время, по результатам исследования учёных Нижегородского национального исследовательского университета им. Н.И. Лобачевского установлено, что «энтропия была и остаётся …ин-струментом, использование которого позволяет проникнуть в глубинные вопросы социальных и политических наук» (Чепьюк, 2016: 64–73). Исследователи из МГТУ им. Н.Э. Баумана предложили применять энтропию для анализа экономической системы предприятия (Соколянский, Войнова, 2014). Исследователи из УрФУ получили положительные результаты об адекватности энтропийного мониторинга социально-экономических систем (Тырсин, Григорян, Антонов, 2019: 23– 26). При расширенном подходе термодинамическая вероятность состояния системы Р nd (6) трансформируется в вероятность состояний системы, например, в меру упорядоченности социальноэкономической системы Р сэ . Назовём её M ψ – мера хаоса системы, так как при увеличении хаоса (ψ - фактора) энтропия возрастает, и при упорядочении структуры (структуировании) системы и упорядочении функциональных связей между её подсистемами и элементами энтропия снижается. Заметили, что ψ - фактор определяется распределением вероятностей состояний системы, а энтропия открытой системы определяется как «сумма произведений вероятностей различных состояний системы на логарифм этих вероятностей, взятая с обратным знаком»¹:

H (X) = -Z^₁h_l\_Ogp_t                                 (7)

где H (X) – энтропия, p 1 p 2 … p i – вероятности состояний x 1 , x 2 , x 3 … x n.

Интересно отметить, что вероятности состояний открытой системы определяются её структурой и функциональными связями между подсистемами и элементами системы. По этому поводу известно, что модель активной системы задаётся её составом, структурой, совокупностью информационных, управляющих и других связей, порядком функционирования и числом его периодов, допустимым множеством состояний (стратегий), информированностью системы. «При этом перечисленные элементы определяют механизм функционирования АС в широком смысле – совокупность законов, правил и процедур взаимодействия участников системы», – отмечали Д.А. Новиков и С.Н. Петраков (1999).

Предположили: в процессе эволюции социально-экономических систем происходит снижение количества нашего знания о новой системе (либо системе, которая приобрела новое качество), иными словами, энтропия возрастает в соответствии с формулой (7).

Доказательство. В такую фазу эволюции социально-экономической системы, как период разрешения диалектического противоречия, её энтропия возрастает, так как вероятности состояний становится более неопределёнными в силу уравнения (1), поэтому энтропия в наибольшей степени стремится к max в периоды зарождения и «заката» социально-экономических систем. Если формой разрешения диалектического противоречия выступает революция, то хаос в системе усиливается, энтропия увеличивается до максимальных значений. В подтверждение своей позиции по данному вопросу сошлёмся на результаты исследований С.Ю. Солодовникова (2018: 5–18), который, опираясь на концепцию Э. Стингерса и И. Пригожина (Пригожин, 1986), установил, что при увеличении энтропии системы увеличивается хаос в отношениях между её элементами и подсистемами: свободная конкуренция ведёт к росту энтропии системы до значений, при которой она прекращает своё существование.

Следовательно, для создания адекватного представления об открытой экономической системе, описания её трансформации как энтропийного процесса, необходимо рассмотреть функциональные связи между её подсистемами и элементами. Констатируя недостаточную изученность функциональных связей, остановимся на исследовании метода количественного математического моделирования упомянутых функциональных связей и зависимостей между элементами, возникающими в процессе эволюции социально-экономических систем. Для математического описания функциональных взаимосвязей в данной работе мы использовали естественнофизический подход: взаимосвязи имеют физическую природу и количественно измеримы. В этом случае показатель эффективности функционирования системы имеет реальное физическое содержание – энергетическое и информационное.

В качестве научной гипотезы ввели меру хаоса системы – M ψ , ψ - фактор хаоса. Предложенный нами ψ - фактор хаоса имеет область его определения, ψ ∈ ψ х . Логично существование множества допустимых и недопустимых состояний M ψ с точки зрения устойчивости функционирования социально-экономической системы. С учётом уравнений (1), (4)–(5), мера упорядоченности экономической системы {1 – M ψ ,} для оценки её эффективности есть энтропия системы: система функционирует эффективно при значении критерия эффективности:

^Н {/} = I^PilogPi < £ (8) гд е ε – критическое для открытой системы значение энтропии, при превышении которой происходит разрушение системы, а мера ψ - фактора входит в область хаоса ψ ∈ ψ х .

Это показано на схеме в виде множеств (рис. 1).

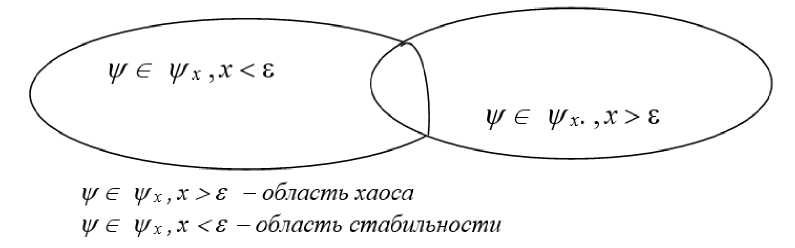
Рисунок 1 – Множества состояний экономической системы

Figure 1 – Sets of States of the Economic System

Данное утверждение расширяет область применения зависимости (8): энтропия возрастает в том случае, когда структура системы усложняется (происходит структуирование системы). Структуированность системы зависит от её иерархии – многоуровневого представления с указанием подчинённости между подсистемами и элементами (стратами), от сотрудничества более организованных частей системы с менее организованными. Энтропия связывает структуру системы, соотношение её связей и частей (морфологию) с эффективностью функционирования.

Как было отмечено выше, в процессе переходов изменяется энтропия системы. Причины изменений – системные противоречия, которые могут быть интерпретированы как необходимые и достаточные условия эволюционного развития, как реализация закона единства и борьбы противоположностей.

Энтропия, как мера эффективности, в наибольшей степени стремиться к max в периоды зарождения и деструкции социально-экономических систем. Этот вывод согласуется с результатами исследований С.Ю. Солодовникова, И. Пригожина и Э. Стенгерса, которые установили: при увеличении энтропии сложной системы увеличивается хаос в отношениях между её элементами и подсистемами. Энтропия связывает структуру системы, соотношение её связей и частей с эффективностью функционирования, развитием и деструкцией. В данном случае показатели эффективности функционирования системы имеет реальное физическое содержание – изменение энтропии, поэтому она применена в качестве критерия: система функционирует эффективно при значении критерия эффективности H(X) ≤ ε, (ε – критическое для открытой системы значение энтропии, при превышении которой происходит разрушение системы). При превышении ε мера {1– M ψ ,} ψ - фактора входит в область хаоса ψ ∈ ψ х . Определены множества допустимых и недопустимых состояний.