Меры сходства музыкальных композиций на основе контентных признаков
Автор: Пчелкин Г.И.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 5-2 (21), 2018 года.
Бесплатный доступ
Статья посвящена обзору методов и метрик определения сходства аудио-композиций на основе признаков аудио-контента. Признаки, такие как низкоуровневые, ритмические, тональные и высокоуровневые, извклекаются из аудио-сигнала композиции. Рассмотрено использование данных признаков в качестве координат для определения расстояния между композициями и для рекомендации сходных музыкальных композиций в рекомендательной системе.
Музыка, кластеризация, рекомендательная система, контентная фильтрация, информационный поиск, мера сходства, метод главных компонент
Короткий адрес: https://sciup.org/140282653
IDR: 140282653
Текст научной статьи Меры сходства музыкальных композиций на основе контентных признаков
Кластеризация методом k-средних и расстояние Васерштейна
Кластеризация методом k-средних с расстоянием Васерштейна была первоначально предложена Logan и Salomon (2001) [1]. Первым шагом является кластеризация вектора признаков целевой песни с использованием метода k-средних. Множество кластеров характеризуется средним, ковариацией и весом каждого кластера, соответственно. Logan и Salomon обозначают множество кластеров как сигнатура песни.
Затем полученные сигнатуры песен сравниваются с использованием расстояния Васерштейна (Rubner, Tomasi, и Guibas, 2000) [2], которое вычисляет минимальный объем работы, необходимый для преобразования одного распределения в другое.
Пусть ^ = { (^, £Р1, W,„ ).....^Lpm, Е^, Wpm ) } – сигнатура песни с m кластерами, где – это среднее, ковариация и вес кластера pi. Пусть Q — { (Mqn ^и 11^i)»•••»(^<г«' ^4», wq„)} – сигнатура другой песни. Пусть dpiqj – расстояние между кластерами pi и qj, которое вычисляется с использованием симметричной формы расстояния Кульбака-Лейблера. Для кластеров pi и qj это имеет вид
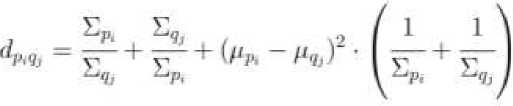
Определим fpiqj как поток между pi и qj . Он отражает стоимость перемещения массы вероятности от одного кластера к другому. Затем все fpiqj определяются таким образом, что общая стоимость W минимизируется.
W определяется как:
m r
4 = ' ^Ч>/ргЧ/ и подвергнуто ряду ограничений. Эти ограничения определяют проблему поиска самого дешевого способа преобразования сигнатуры P в сигнатуру Q, что может быть сформулировано как задача линейного программирования и эффективно решена. После того как все fpiqj найдены, расстояние рассчитывается как:
EMD^P.Q^ =
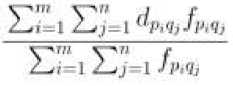
Magno и Sable (2008) [3] представили немного иной вариант этой меры сходства. В их версии каждый кластер соответствует гауссовой компоненте для формирования модели гауссовой смеси (GMM). Magno и Sable, а также многие другие авторы (например, Celma (2010) и Mandel и Ellis (2005)), ошибочно утверждают, что Логан и Саломон использовали метод k-средних для обучения параметров GMM, когда фактически они использовали кластеры k-средних для моделирования песен и вообще не использовали GMM.
Модели смеси нормальных распределений и метод Монте-Карло
Aucouturier и Pachet (2002) [4] представили использование GMM (модели смеси нормальных распределений) для моделирования песен. Их подход состоит из двух этапов, первым из которых является кластеризация векторов признаков MFCC с использованием GMM. GMM оценивает плотность вероятности как взвешенную сумму M более простых гауссовских плотностей, которые часто называют компонентами. Aucouturier и Pachet дают следующую формулу GMM:
М
P где n - размерность вектора признаков. Aucouturier и Pachet использовали три гауссовых распределения на смесь, но в более поздней оценке (2004) [6] было обнаружено, что использование большего количества гауссовых компонентов дает лучшие результаты. Наилучшие результаты были достигнуты при использовании 20 MFCC и 50 гауссовых компонентов. Реализация этого метода, выигравшая конкурс классификации жанров ISMIR 2004, использовала 30 гауссовых компонентов (Pampalk, 2004) [6]. Как описано Pampalk (2006) [5], параметры GMM, 0 = {pm, Zm, Cm | m = 1..M }, должны оцениваться для каждой GMM, то есть для каждой песни. Оптимальная оценка параметров максимизирует вероятность того, что вектор признаков Ft = {x1, .„, xn} был сгенерирован GMM. Логарифмическая вероятность является широко используемой мерой для вычисления вероятности и вычисляется как: ЦГ^ = к^Р^б) = ^tog^O).Fl Л Хорошие оценки параметров могут быть найдены с использованием алгоритма максимизации ожиданий (EM-алгоритм), хотя исходные оценки могут быть случайными или вычисленными с использованием других алгоритмов кластеризации. Aucouturier и Pachet использовали метод k- средних для вычисления начальных параметров. EM-алгоритм состоит из двух шагов. Первый шаг - вычислить математическое ожидание, которое является вероятностью того, что наблюдение xn было порождено m-ым компонентом. Формула для шага ожидания: Р('Тц I Ш,О)( 1Г| Л (ти, Цт». Е,л )( т Phnli^,^ =---------= —---------------. Второй шаг EM-алгоритма - максимизация ожидания, в котором параметры пересчитываются на основе ожиданий. Формулы этапа максимизации: Е» P(m|r„.9)r„ Е^О^-е) En Р(г»кг„в)(т„ - /troX^n - р,„)Г Е.-ЛтК-В) = Y^P(mkn.9) После того, как GMM сформированы, вторым шагом подхода является вычисление сходства между кластерными моделями, то есть песнями. Это делается путем выборки сэмплов из GMM, представляющих песни A и B. Пусть эти сэмплы будут X и X. Aucouturier и Patchet отмечают, что процесс выборки примерно соответствует воссозданию песни из ее тембральной модели. Процесс выборки называется методом Монте-Карло. Логарифмическая вероятность L(X | Θ) вычисляется для каждой комбинации песня/сэмпл, и её результаты используются для вычисления расстояния. Оно вычисляется так: dAn цхл|ел) + цхи\ои^ - ь(хл|в") - £(хй|вл) Pampalk (2006) [5] отмечает, что L(X | 0е) и L(X | 0A) обычно имеют разные значения. Применяются оба из них, так как для большинства приложений желательна симметричная мера сходства. Кроме того, для нормализации результатов добавляется самоподобие, и в большинстве случаев справедливы неравенства L(X | 0A) > L(X | 0A) и L(X | 0A) > L(X | 0B). Средние векторы признаков и евклидово расстояние Tzanetakis and Cook (2002) [7] представили простой метод, в котором средние и дисперсии спектрального центроида, спектрального спада частотной характеристики, спектрального потока, пересечения нулей во временной области, низкой энергии и первых пяти коэффициентов MFCC были объединены в один 19-мерный вектор признаков. В дополнение к тембральным признакам они использовали шесть ритмических признаков контента и пять признаков основного тона, что образовало 30-мерный вектор признаков. Tzanetakis и Cook подготовили GMM для задач жанровой классификации с использованием векторов признаков. Тем не менее, Magno и Sable (2008) [3] использовали евклидово расстояние, чтобы определить сходство векторов признаков, поскольку векторы можно сравнить, используя стандартные меры расстояния. В другой работе Tzanetakis (2002) [8] использовал расстояние Махаланобиса, чтобы сравнить векторы, ссылающиеся на разные динамические диапазоны признаков, и их вероятностную корреляцию в качестве причины для ее использования вместо евклидового расстояния. Фактически, Tzanetakis утверждает, что только наивное выполнение поиска подобия будет использовать евклидово расстояние. Нормальное распределение и расхождение Кульбака-Лейблера Mandel и Ellis (2005) [9] представили метод, использующий одно гауссово распределение с полной матрицей ковариации для моделирования песни. Для сравнения двух моделей Гаусса они использовали расхождение Кульбака-Лейблера (KL). Для двух распределений p(x) и q(x) оно определяется следующим образом: Существует замкнутая форма КЛ-расхождения для одиночных гауссианов: где d – размерность x, а Tr(M) – след матрицы M. Поскольку Mandel и Ellis использовали КЛ-расхождения как ядро метода опорных векторов (SVM), его пришлось модифицировать, чтобы удовлетворить условиям Мерсера. Условия не выполняются, поскольку КЛ-расхождение не является ни симметричным, ни положительным. Чтобы симметризировать KL-расхождение, Mandel и Ellis суммировали два расхождения: DkiM КЦр\\дНКЦд\\р\ Другое условие Мерсера может быть выполнено путем возведения экспоненты в степень элементов этой матрицы, поскольку это создаст положительно определенную матрицу. Конечная матрица имеет элементы: К(Х,.Х^ = е-°^{Х' ^‘ где y — параметр, который может быть настроен для максимизации точности классификации. Для KL-расхождения между двумя GMM не существует решения закрытой формы, поэтому оно должно быть аппроксимировано. Bogdanov и др. (2009) [10] сравнивают песни Xи Y, смоделированные с использованием GMM, содержащих одну гауссову компоненту с симметричной аппроксимацией КЛ-расхождения закрытой формы: <11X. У) = TrfE^Ey) + Тг(Еу‘Ел)+ + Тг^Х"^' + Ey^fpx — ИгНих — РуУ^ — 2ХыгсСч где Цх и ^Y являются средними MFCC, Хх и XY - ковариационные матрицы MFCC, а NMFCC - число используемых MFCC. Евклидово расстояние на основе метода главных компонент Cano и др. (2005) [11] использовали евклидову метрику для сравнения векторов признаков. Bogdanov и др. (2009) [10] консультировался с Cano по используемой методологии, так как указанный источник не содержал конкретных деталей. Cano и др. нормализовали данные признаков до интервала [0, 1], а затем использовал анализ главных компонентов, чтобы уменьшить размерность векторов признаков до 25 переменных. Затем сравнения выполнялись в уменьшенном пространстве признаков. Эта мера сходства не использует MFCC, в отличие от всех других описанных мер. Она использует обширный набор признаков, представляющих тембральные, ритмические и тональные аспекты песни. К ним относятся различные спектральные особенности, такие как спектральный центроид, распространение и эксцесс. Ритмические аспекты представлены громкостью биений и тональными аспектами с помощью непереведенных гармонических характеристик класса основного тона и силы ключа.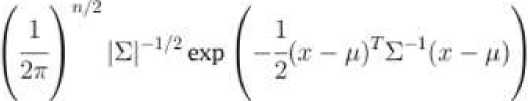
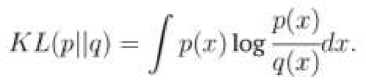
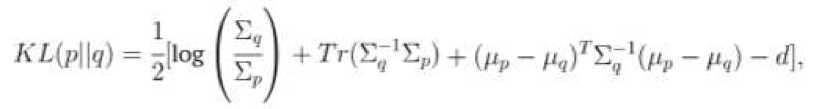
Список литературы Меры сходства музыкальных композиций на основе контентных признаков
- Logan, B., & Salomon, A. (2001). A music similarity function based on signal analysis. In Proceedings of the 2001 IEEE International Conference on Multimedia and Expo (стр. 745-748).
- Rubner, Y., Tomasi, C., & Guibas, L. J. (2000). The earth mover's distance as a metric for image retrieval. International Journal of Computer Vision, 40 (2), 99-121.
- Magno, T., & Sable, C. (2008). A comparison of signal based music recommendation to genre labels, collaborative filtering, musicological analysis, human recommendation and random baseline. In Proceedings of the 9th International Conference on Music Information Retrieval (стр. 161-166).
- Aucouturier, J., & Pachet, F. (2002). Music similarity measures: What's the use? In Proceedings of the 3rd International Conference on Music Information Retrieval (стр. 13-17).
- Pampalk, E. (2006). Computational models of music similarity and their application in music information retrieval (PhD thesis, Vienna University of Technology, Vienna, Austria). Доступ: http://www.ofai.at/~elias.pampalk/publications/pampalk06thesis.pdf
- Pachet, F., & Aucouturier, J.-J. (2004, April). Improving timbre similarity: How high is the sky? Journal of Negative Results in Speech and Audio Sciences, 1-13.
- Tzanetakis, G., & Cook, P. R. (2002). Musical genre classification of audio signals. IEEE Trans. Speech and Audio Processing, 10 (5), 293-302.
- Tzanetakis, G. (2002). Manipulation, analysis and retrieval systems for audio signals (PhD thesis). Princeton University, Princeton, NJ, USA.
- Mandel, M. I., & Ellis, D. (2005). Song-level features and support vector machines for music classification. In Proceedings of the 6th International Conference on Music Information Retrieval (стр. 594-599).
- Bogdanov, D., Serrà, J., Wack, N., & Herrera, P. (2009). From low-level to high-level: Comparative study of music similarity measures. In Proceedings of the 11th IEEE International Symposium on Multimedia (стр. 453-458). IEEE Computer Society.
- Cano, P., Koppenberger, M., & Wack, N. (2005). Content-based music audio recommendation. In Proceedings of the 13th Annual ACM International Conference on Multimedia (стр. 211-212). ACM.


