Место основного уравнения общей теории относительности в системе физико-геометрических знаний

Введение . Основное уравнение ОТО - это уравнение гравитации Эйнштейна А. Посредством дифференциальной геометрии расслоенных пространств внутренних степеней свободы уравнение Эйнштейна А .

строится строго математически. И оно входит в общую единую систему физико-геометрических знаний. Уравнения с формой данного уравнения, его физико-геометрической связью возможны практически во всех разделах физики (электричестве, магнетизме, термодинамике, естественно, механике)

Актуальность проблемы . Математик Р.Герман (Robert Hermann, Department of Applied Sciences, Harvard University, Cambridge, Massachusetts) : «...я твердо верю в дальнейший прогресс этих исследований. Методы дифференциальной геометрии настолько интересны и глубоки, что они должны привести к лучшему пониманию разнообразных нелинейных явлений. [8, с.47 ]

… тема достаточно богата для того, чтобы обеспечить бурный рост, если создать достаточно плодотворную почву. Мы видим здесь классический пример новой математики и физики.» [8, с.68 ].

Геометрические основы [2]. Рассматривается расслоенное пространство X , образованное топологическим произведением пространства Х_п (база) и пространства значений дифференциальногеометрического объекта S . Базовое пространство Х_п гомеоморфно n -мерной области пространства Эвклида. Каждой точке P е Х_п относятся n чисел (координаты) J , где i = 1.2.3, ..., n из некоторой области арифметического пространства. J i являются в физике обобщенными криволинейными координатами ( x, y, z, t, температура, энтропия, теплоемкости, термодинамический потенциал и др.).

Х_п - пространство класса m , так как постулируются преобразования, образующие псевдогруппу класса m , то есть имеются дифференцируемые до порядка m ( m >  0) и взаимно-однозначные преобразования координат

J = f‘j ^j ), i , J = 1, 2, 3, .,n . (1)

В физике эти преобразования являются естественными, то есть имеют силу преобразования координат, допускаемые законами физики. Примером таких естественных преобразований в физике являются преобразования Лоренца в СТО.

Пространство значений дифференциально-геометрического объекта E есть касательное пространство, которое является однородным пространством Клейна, фундаментальной группой которого служит общая дифференциальная группа Ли с параметрами, значения которых f, f^,..., f^2-j индуцируются преобразованиями (1), образуя систему значений частных производных функции (1) в точке P е Хп.

Дифференциально-геометрическим объектом E класса m в точке P е Х_п называют конкретное представление группы Ли в виде группы преобразования

— а —а   п      .

E = F S ^в , f ‘ , к

— i f j1 j 2,•••,

\

m

.

Пространство значений E гомеоморфно некоторой области пространства Эвклида N измерений.

Преобразования (2) определяют тип объекта (скаляр, спинор, вектор, тензор более высокого ранга).

Геометрические структуры расслоенного пространства в СТО .

В СТО реализуются расслоенные пространства внутренних степеней свободы  Xn^N   [2], образованные топологическим произведением пространства X    (база) и пространства значений дифференциально геометрического объекта E.

Не теряя общности изложения, ограничимся двумерным базовым пространством с координатами ^, где i = 0,1 , и слоевыми координатами 1    д ^¹       ₂   д^²

П =      , п =       , где t - параметр, п и П - проекции вектора.

д t              д t

Слоевое пространство имеет также N = 2 измерений.

Если П = П № ) , тогда имеем дело с векторным полем.

Величинам придадим физический смысл. t - время, П и п² - проекции вектора скорости. Размерность [п' ] = [ п ²] = м— • сек .

Метрическую функцию     F( g , П ) построим на основе СТО.

Геометрические требование: она должна в каждой точке P ∈ X являться однородной функцией степени один в слоевых координатах и однородной функцией степени нуль в базовых координатах (чтобы сохранялась физическая размерность). Вводим постоянную составляющую вектора η . Такой составляющей вектора служит величина , являющаяся скоростью света с . Составляющая    является проекцией вектора скорости на ось x

(возможно и на ось у, и на ось z ), Метрическая функция F ( g , П )

определяет длину вектора η. Возведем метрическую функцию в квадрат, получим функцию F2 (g, ni), которая является однородной функций степени два в слоевых координатах.

Представим ее в виде:

F² = ап ⁰ 3 Л ¹² , где а - постоянная, Л = п ⁰2 - П 1 • В ОТО данная функция имеет размерность Дж/м³ ).Не теряя общности изложения, ограничиваемся стационарным полем. Если α является массой (релятивистской массой), то получаем известную формулу СТО Е = mc².

Заметим, что в СТО можно построить многообразие различных метрических функций.

Здесь же построена простейшая метрическая функция.

Дальнейшие действия будут проходить в соответствии с работой [4].

Имеется дуальное пространство с координатами ζ , которые определяются следующим образом

1 дF²

2 дп •

Тогда получаем конкретные составляющие ковариантного вектора:

ζ = ³ αη ⁰² Λ^{- 2} - ¹ αη ⁰⁴ Λ^- 2

ζ ₀ = αη Λ - αη Λ ,

Они приводят к соотношению

ζ i η ⁱ = F ² .

ζ ₁ = ¹ αη ⁰³ η ¹ Λ^{- 32} .

При подстановке составляющих вектора получаем тождество.

Вывод: составляющие ковариантного вектора найдены правильно.

Составляющие метрического тензора находим по формуле:

1   ∂ ² F ²

^ij 2 ∂ η ⁱ ∂ η ^j .

Это есть однородные функции степени нуль в слоевых координатах.

Размерность кг .

G ₀₀ = ³ ₂ αη ⁰ Λ^{- 12} - ⁷ αη ⁰³ Λ^{- 2} + ³ αη ⁰⁵ Λ^{- 2} ,

G = G = ³ αη ⁰² η ¹ Λ^{- 2} - ³ αη ⁰⁴ η ¹ Λ^{- 2} ,

G = ¹ αη ⁰³ Λ^{- 2} + ³ αη ⁰² η ¹² Λ^{- 2} .

Имеем

F ² = G_ij η ⁱ η ^j .

получаем найдены

Подставим в нее составляющие метрического тензора, тождество. Вывод:  составляющие метрического тензора правильно.

Коэффициенты связностей находятся по формуле ijk 4 ∂ηi ∂ηj ∂ηk .

Получаем

C = 3 α Λ- 12 - 27 αη02 Λ- 2 + 36 αη04 Λ- 2 - 15 αη06

= α       αη    + αη        αη,

C001=C010= C100 = 32αη0η1Λ- 2 - 21 αη03 η1Λ-52 + 15 4αη05η1 Λ-72 ,(9)

^C 111 ⁼     αη ⁰³ η ¹ Λ^{- 2} + ¹⁵ αη ⁰³ η ¹³ Λ^{- 2} ,

С =С =С =   ап02 А 32 -   an0" А 52 + ^ ап0 2 п12 А 52+ 1^ ап0" п12 А 72

C ioi C lio C oil /4 ^аЧ ^л     /4 ^аЧ ^л + /4 ^ч Ч ^л + /4 ^аЧ Ч ^л

Данные коэффициенты связностей удовлетворяют условиям Эйлера: с^ = с п= с П = 0 .               (10)

Подставив в него коэффициенты связностей и составляющие векторов, получаем тождества. Вывод: коэффициенты связностей найдены правильно.

Первый тензор кривизны имеет вид [4]:

S jkh = Ak r A rh - A rh A rk .                                  (11)

гДе    A ir = FC r .

Свернем индексы следующим образом: 2                               pn mr ik              pki rnm       rkn pim               .

Получили тензор типа тензора Риччи в римановой геометрии [3], который используется в ОТО. В уравнении гравитации в ОТО он приравнен к плотности энергии-импульса. В случае релятивисткой массы получаем размерность [ S_ik ] = [ Sф ] = Дж^. сек . В геометрии размерность м⁵

[ s ik ] = 4. м

Чтобы перейти к геометрическому тензору Sг следует ввести две постоянные у и c с размерностями

Н. м2        м

[/] = ---— , [ c ] = --- и кг          сек

помножить

Sф на Y . Окончательно получаем с г = У фф Sik      2 Sik

.

с

Заметим, что S ^Ф содержит ¹ . с²

Это уравнение сохраняет физико-геометрические связи основного уравнения ОТО. Если к левой части добавить член 1 G S , а правую часть умножить на 8п, где S г

– скалярная кривизна пространства, то полученное уравнение

S ik + ¹ G j S = 8 *4 S ф

2              с ²

совпадает с основным

уравнением ОТО - уравнением Эйнштейна А.,  как по физико геометрическому содержанию, так и по форме.

Уравнение гравитации в ОТО, например, Ландау Л.Д. и Лифшиц Е.

М. [1] получают посредством принципа наименьшего действия, приравнивая геометрические и физические величины (тензор Риччи, скалярную кривизну риманова пространства и плотность тензора энергии-импульса). Этим самым постулируется, что энергия-импульс искривляют пространство-время. В ОТО введены физические величины и с. При приравнивании геометрических и физических величин использовались две Н. м          м размерные величины:'- и с с размерностями   [у] =—~  и [с] = — • И кг             сек в самом начале изложения они объявляются соответственно гравитационной постоянной и скоростью света. Это не совсем корректно. Физическое содержание у раскрывается при соблюдении принципа соответствия: ОТО в пределе должна сводиться к теории Ньютона. Здесь и раскрывается физическое содержание у. Она является гравитационной постоянной. Ее численное значение получают экспериментально. Физическое содержание постоянной с раскрывается при получении в ОТО волнового уравнения, где постоянная с является скоростью гравитационной волны. Численное значение этой постоянной найдено экспериментально: оно совпадает со скоростью света.

Величины / и с имеют числовые значения. В уравнении ОТО они образуют комбинацию

^Y = ¹

c ⁴    12.2.10 ⁴³ H

и — = 12.2.10 43 H .

У

Уравнение (13) также содержит эту комбинацию.

Получается, что в правой части уравнений содержится две физические величины: плотность энергии-импульса в числителе и в знаменателе - силу, числовое значение которой 12.2.1043 H . Таким образом, на кривизну пространства-времени влияет не только плотность энергии-импульса, но и сила.

Для соблюдения преемственности разумнее представлять уравнение (13), как и основное уравнение ОТО, в форме 12..2 10 43 SГ_к = c² S ф

H Дж

Размерность уравнения — =     .                .

мм

Рассматриваемые уравнения фактически отображают единую физикогеометрическую связь формул напряженности, потенциала гравитационного поля и закон Ньютона. Например, в теории тяготения закон Ньютона представляется формулой у ^Мт = F , где М и m - r

H  Дж массы, F - сила. Размерности совпадают, а именно, — =    . Здесь м2   м3

простая зависимость – гиперболическая  (размерность -    ¹ ). В

м рассматриваемых уравнениях геометрическая зависимость сложная: в ОТО она задана тензором Риччи (размерность -  1  ), а в построенных м2

уравнениях она задана тензором, построенным на основе первого тензора кривизны Картана. f S^г , где f - сила, является давлением (размерность Па ).

Конкретный пример. Определим S ^Ф . Для этого подставим в выражение

S^Ф контравариантные тензоры тензорам (6) и конкретные значения (9)

при £   =   0 и z =   0. Получаем     S_o ф = S_oo = -    F ² Q ,

^{00     00}      4 c ²

S 00 = - ⁹ 4 F² & .                                (14)

4 с

Геометрические структуры расслоенного пространства в электромагнетизме.   В электромагнетизме также реализуются расслоенные пространства внутренних степеней свободы X [2]. В этой связи и в электромагнетизме возможно построение с привлечением геометрии расслоенных пространств внутренних степеней свободы уравнения, которое сохраняет основные связи и форму основного уравнения ОТО.

Ограничимся трехмерным слоевым и базовым пространством с df координатами f, где i = 0,1, 2, и слоевым координатами n^ = ~, dt df

П = —^- , n =     , где t - параметр, n , n и n - проекции вектора.

d t            d t

Величинам придадим физический смысл. t - время, n0   n1   и n2 - проекции вектора напряженности электрического поля. Размерность

H

[[n0]] = [n4 = [n2] = —. Вектор n является касательным вектором к линии Kл электрической индукции.

Квадрат метрической функции F ² представим в виде:

F ²

S o ^S

n n'n2

<     7

ⁿ = ^S o

4 n nn2

,

где s - фундаментальная электрическая постоянная с размерностью

Ф [ S o ] = -, м

£

n ⁰

Пп ²

<     7

диэлектрическая «постоянная» (безразмерная). Она

является функцией составляющих напряженности электрического поля, т.е. состояние среды зависит от электрического поля. Здесь возможны разные варианты: F2 = £0£

-Е

Е Е

< х У 7

Е ² = £ z     ^S 0

——

Е Е

< х у 7

, F ²

^S 0 ^S

Е Е <  ^z У 7

Е2 = s x   S0

ЕЕ

< ^z у 7

и др.

Данный квадрат метрической функции отвечает геометрическому требованию: он является однородной функцией степени два в слоевых координатах, размерность [ F ²] = ^Дж , как и в ОТО.

м ³

Заметим, что в электромагнетизме также можно построить многообразие различных метрических функций.

Здесь же построена простейшая метрическая функция.

Дальнейшие действия будут проходить в соответствии с работой [4].

Также имеется и дуальное пространство с координатами ζ , которые определяются по формуле (3).

Тогда получаем конкретные составляющие ковектора:

„     03                         04                          04

2 ε ₀ η ⁰          ε ₀ η           ε ₀ η ⁰

ζ ₀ =     _{1 2} , ζ ₁ = -      ₂     . ζ ₂ = -      ₂    .

η η         2 η ¹ η ²        2 η ² η ¹

Они удовлетворяют условию (4).

Составляющие

метрического тензора

находим по формуле (5).

Получаем

^G 00

6 ε ₀ η ⁰² η ¹ η ²

,

^G 10

-

0³ 2 ε ₀ η ⁰

I2 2

η ¹ η ²

,

^G 02

-

0³ 2 ε ₀ η ⁰

2 ^, η ¹ η ²

G 12

ε ₀ η ⁰⁴ 2 η ¹² η ²²

,

^G 22

ε ₀ η ⁰⁴ 2 η ¹ η ²³

.

G 11

0⁴ ε ₀ η ⁰

η ¹ η ²

.

Это есть однородные функции степени нуль в слоевых координатах.

Они удовлетворяют уравнению (7).

Коэффициенты связностей находятся по формуле (8). Получаем

6 ε ₀ η

С ₀₀₀ =           , С ₁₁₁

η ¹ η ²

-

3 ε ₀ η ⁰⁴

₄    , C ₂₂₂

2 η ¹ η ²

-

0⁴ 3 ε ₀ η ⁰

⁴ 2 η ¹ η ²

с = с = с = ,   112 =   121 =   211 =

-

0⁴ ε ₀ η ⁰

3     2 ^,

2 η ¹ η ²

с = с = с =

122 =   221 =   212 =

-

ε ₀ η

_{2  3} . С ₀₂₂ = С ₂₂₀ = С ₂₀₂ =

2 η ¹ η ²

2 ε ₀ η

3    С 002 = С 200 = С 020 =

η ¹ η ²

-

0² 3 ε ₀ η ⁰

1    22

η ¹ η ²

с = с = с = 001 =   100 =   010 =

-

3 ε ₀ η ⁰²

I² 2 η ¹ η ²

С = с = с =

011 =   101 =   110 =

2 ε ₀ η ⁰³

³ η ¹ η ²

Данные коэффициентов связности удовлетворяют условиямю Эйлера (10).

Здесь также используем первый тензор кривизны (11) и тензор, полученный двойным свертыванием его индексов (типа тензора Риччи в римановой геометрии) (12). Имеем размерность [ S_к] = [ S ф ] = Дж К .

ik ik м³ Н

В геометрии размерность Sfk = 1— м2

Чтобы перейти к геометрическому тензору S ^г следует ввести две

Н . м        м

-

постоянные [y] = ——, [c] = —, как в ОТО, и третью постоянную e кг2          сек с4

элементарный заряд ([e] = Кл) и умножить  Sф на —у. Окончательно уе получаем Sr = с ^.

γ е

Это уравнение также сохраняет физико-геометрические связи основного уравнения ОТО и совпадает с основным уравнением ОТО как по физико-геометрическому содержанию, так и по форме.

Конкретный пример. Определим SГ2 (= S2\) . Для этого в выражение (12) S Ф подставим контравариантные составляющие составляющих тензора (17) и конкретные значения (18) при i = 1 и k = 2. Получаем

.

S г 2 = -с т F² —

12        _2

Y е     Пп

Это уравнение сохраняет структуру физико-геометрическую связь формул для потенциала, напряженности и закона Кулона для электростатического поля.

Геометрические структуры в термодинамике. Метрических функций в термодинамике также многообразие. Пример. Введем трехмерное базовое пространство с координатами 4, где i = 0,1,2, и трехмерное слоевое пространство:  4° = ПТ - работа одного моль вещества, 41

-

тепло,

подводимое (отводимое) к одному моль вещества, 42 - внутренняя энергия одного моль вещества, τ - абсолютная температура. Слоевые координаты д4\ следующие: универсальная газовая постоянная  п0 (= “^), молярная

∂τ теплоемкость при постоянном объеме П (= de), молярная теплоемкость дт де при постоянном давлении п^ (= —). См. рисунок. дт n = \dQ |

^^в  Id О J _в

R =|- 1 , Id T ) p

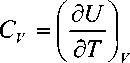
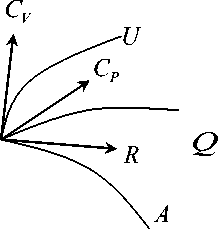
Здесь действия осуществляются в рамках теории обобщенных координат, основы которой были заложены Лагранжем, Гамильтоном, Эйлером и др. Действия, таким образом, распространяются на дифференциальную геометрию расслоенных пространств внутренних степеней свободы X .

Метрическую функцию выберем в виде:

F ? i П)=

П 0 т

? - ?

Ch

k

n2

-

n1

n0

- ¹

Она является однородной функцией степени один в слоевых координатах. Определим ее физический смысл. Запишем уравнение индикатрисы в виде:

F ( ? , П ) =

1 e - ?

i

Ch

Л 2      1

k 'I

П ° т = I ,

^{- 1}

где ? - фиксированы и П - переменные. Откуда следует

Ch k

И ² - ^п п⁰

П⁰ т = ?²

-

е .

- ¹

Данное равенство является первым началом термодинамики для реального газа.    Функция f = —

Ch

RF

7     '/

—

характеризует эффект отхождения

реального газа от идеального. Если данная функция равняется единице, то есть газ идеальный, тогда получаем первое начало термодинамики для идеального газа п 0 т = f ² — f ¹.

Функция f = 1 приводит к уравнению Майера п ² — П = П ⁰ ( Ch 0 = 1 )

Выбранная в качестве модельной функции функция f = —

Ch

(

7 V

—

^ 1, 7

заслуживает внимания по той причине, что она удовлетворяет модифицированному нелинейному уравнению Кортевега-де Вриза . Ее же квадрат f ² является решением нелинейного уравнения Кортевега-де Вриза (солитонное решение). Эта функция и составляет основу в данном примере геометрического описания термодинамической системы с привлечением расслоенных пространств внутренних степеней свободы.

Итак, для точек индикатрисы (как и фигуратрисы) выполняется первое начало термодинамики, а именно, например, подводимое тепло идет на изменение внутренней энергии газа и на совершение работы идеального и реального газа. Для точек, лежащих вне индикатрисы, подводимое тепло переходит во внутреннюю энергию, идет на совершение работы газом и превращается в другие виды энергии.

В качестве следующего примера мы за основу построения метрической функции в термодинамике примем метрическую функцию (15), добавив координаты базового пространства в комбинации О = j^^ —^, где к -постоянная Больцмана , N - число Авогадро , и в качестве базовых координат примем базовые и слоевые координаты термодинамики, которые изложены выше.

Квадрат метрической функции расслоенного пространства, таким образом, будет иметь вид:

F² ( fi, т / ) = О

4 т п п

.

Данная функция однородна степени два в слоевых координатах. Естественно, сама функция является однородной степени один в слоевых координатах. Геометрическое требование, таким образом, исполняются.

Представим функцию (20) в форме:

F 2te J) =dl ⁿ ]= f . где f = -^0^               (21)

^ nn J te — %)            kN A nn

Выбранная таким образом метрическая функция сохраняет основы термодинамики.

И в этом случае физический смысл получают геометрические понятия «индикатриса» и «фигуратриса».

Уравнение индикатрисы имеет вид:

F tenH  : f = I, где te - фиксированы и П - переменные. Откуда следует f 0т =? - te.

Получаем первое начало термодинамики для «реального» газа. Функция f характеризует эффект отхождения «реального» газа от идеального газа. Для точек индикатрисы (как и фигуратрисы) выполняется первое начало термодинамики, а именно, например, подводимое тепло идет на изменение внутренней энергии газа и на совершение работы «реального» газа. Для точек, лежащих вне индикатрисы, подводимое тепло переходит во внутреннюю энергию, идет на совершение работы газом и превращается в другие виды энергии (диссипативный процесс). Поскольку за основу построения в термодинамике метрической функции принята функция (20), сходной по форме с функцией (15), то все значения ковектора (16), составляющих метрического тензора (17) и коэффициентов связностей (18) имеют силу и в термодинамике с поправкой на © и с введением термодинамических величин:

ковектор с составляющими _ 2®ц °         _   © П ° Z 0 =     12 ,      z 1 =           2 . ЦЦ            2 ц ц

04 с 2 = -° П ,•               (22) 2 ц ц

Они удовлетворяют уравнению (4);

метрический тензор с составляющими

G 00	6 Θ η 02	G 10	2 Θ η 03	G 02	2 Θ η 03
	η 1 η 2   ,		η 12 η 2 ,		2 , η 1 η 2	(23)
G 12	Θ η 04	G 22	Θ η 04	G 1 1	Θ η 04
	2     2, 2 η 1 η 2		2 η 1 η 23 .		η 13 η 2

Они удовлетворяют уравнению (7); коэффициенты связностей

с = с =с =

002      200     020

3 Θ η ⁰² _η 1 _η 2²

с = с = с =

,    001      100     010

3 Θ η ⁰²

2      , С 011    С 101    С 110

η ¹ η ²

2 Θ η ⁰³ η ¹³ η ²

= 000	6 Θ η 0 1   2   , С 1 11	3 Θ η 04 -     4    , C 222	3 Θ η 04 -        4 , С 112    С 121   С 211	Θ η 04
				3     2 ,
	η 1 η 2	2 η 1 η 2	2 η 1 η 2	2 η 1 η 2

Θ η ⁰                 2 Θ η

₁₂₂    С ₂₂₁   С ₂₁₂   -     _{2  3} ,    С ₀₂₂    С ₂₂₀   С _{202           3}

2 η ¹ η ²                       η ¹ η ²

Они удовлетворяют уравнениям Эйлера (10).

Конкретный пример. Определим Sг ( Sг ) . Для этого подставим в выражение (12) SФ контравариантные составляющие тензора (23) и конкретные значения (24) при i = 1 и k = 2. Получаем г        ξ0       R 3

¹² kN A ( ξ ² - ξ ¹ ) C V ² C P ²

Физическая размерность отсутствует. Если ограничиться только

ξ ⁰      R ³

постоянной Больцмана, а именно, Sг               , то получим размерность моль.

Введение коэффициентов нелинейных связностей расслоенного пространства внутренних степеней свободы в термодинамику. Изложение следует работам [4] и [5].

Введем пространство Финслера F n с базовыми координатами ξ ⁱ   ( i

= 1,2,3).

В Fn введем векторное поле ηi (ξi) (контравариантный вектор). Вводим метрическую функцию F(ξi,ηi) в каждой точке ξi ∈F , которая является однородной функцией степени один в слоевых координатах и однородной функцией степени нуль в базовых координатах. Функция F(%, п) определяет длину вектора п. Для удобства переходят к функции f 2(%i, П), которая является однородной функцией степени два в слоевых координатах.

Выберем ее в виде функции (20) и представим в форме:

F ² ( % i , П ) = ©f П ^ X   % f , где f = П ^,  ₀ =    ^    .         (26)

^ Пп ² ) ( % - %)           пП ²        ( % - % )

Физическое содержание введенных величин такое же, как и в предыдущем примере.

Составляющие метрического тензора определяем по формуле (8).

Получаем

(   02 к ]	6 ( 2п 0 1	f п_ 1 1 п1 ) f п °2 2	f 2 п 0 1 п2 f п 02	J 1	J J J , G 'j ) = JJ	к 1 2 к п п |	3 2 f 2 п 1	f 2 п 1 1 к п 0 J f 4 п 121	f 2 п 2 1 к J ' 2 пп 2 1	(27а,в)
	1 п ) ( 2 п “ 1	1 п ) f п °2	^ 2 п'п2 f п 0 2	JJ )		U02 J	к п 0) f 2 п 2 1	о 2    1 к п   ) 2 п‘п 2 )	0 2 < п / f 4 п 2 1
	к п 2 J	! 2 пП2	к2 к п )	J	JJ		к п 0 J к к     )	. п 0 2 J	„о2    1 к п   ))

Имеем

F ² ( % , п ) = G ij ( % , п Мп^j   и   ds ² = F ² ( % , d % ) = G j ( % , d % ) d % d % .

Абсолютные переносы составляющих контравариантных векторов осуществляются по формуле sn= dn+Гk (%, п)d%,                                             (28)

где Г к ( % , n ) - нелинейные связности, зависящие от поля. Эти функции являются однородными степени один в слоевых координатах.

Параллельный перенос будет, если 5 п = 0. Аналогичные действия проводятся с ковариантным вектором, составляющие которого Z , Имеем        Z = F( % , п ) tF^ .

дп

Имеем Z= G ij ^f , n ) n ^j ,      ^C = G „ & n ) .

дП

Абсолютный перенос составляющих ковариантного вектора Z находится по формуле.

2                  2

зс = dQ-Гк f, C) df, где  Г * f,C) - нелинейные связности, зависящие от поля. Эти функции также являются однородными степени один в слоевых координатах.

Параллельные переносы приводят и к соотношениям:

R F - Z Г k 1

[дf ^k F J

= 0 .

дF , х к дF dF = —ddq +---di = df д^    дП

Вводятся и отношения:

1 ‘2

I j ( f , n ) = ^дГ k ^{f , n} ) ,   Г*(Z C ) = ^{дГ jk} f , ^C ) ,

(31а,в)

дцк

1 ‘                                 1 ‘                         2 ‘2

г jk f , n ) n ^k =ГА£,п );   I    f , C ) C i =г jk ( f , C ) .

Уравнение геодезических имеет вид:

df- + 2Gi (f, n) = 0,(32)

ds где G = GiG = - Gjl^-F^ nk— ^F^| j 4 [дПSfд^

Коэффициенты нелинейных связностей пространства внутренних степеней свободы индуцируют следующие тензоры кривизны:

i

R

i

д Г

hk =

h

д f

—

д Г k

д f

+

Гjk

^j h

—

Гjh

^j k ^,

R ihk =

д Г- h

д Г -k

д f

—

д f

+ r ik

Г jh

—

^j Г i h Г jk .

Определим Gⁱ .

Для

этого подставим в данную формулу квадрат

метрической функции и составляющие контравариантного метрического тензора (27в). Получаем:

G0

—

п ⁰ ( %² п ⁰ — % п⁰ + %⁰ п¹ — %⁰ п ²)

2 % ° ( %‘ — % ²)             ^,

G1

₌ п ( % п ⁰ — % п ⁰ + % п — % п ² ) 2 % ( %' — % )          ^,

G2

—

п ² ( %² п ⁰ — % п⁰ + %⁰ п¹ — % ⁰ п ² )

2 % ⁰ ( % ' — % ²)              .

Получим нелинейные связности. Для начала используем формулу

1 ₌ д ^ %т )

^hk дп ^к д ц^к

.

Подставим в нее выражения (34). Получаем

1 0 0    ^-0 ,

Г 01 = Г 10 =

—

2 % — % ) ’

Г 02 = Г 20

= 2 % ' — % )

1 0

,       ₁₂

1                1

= Г 21 = Г 11

1 22

= 0 ,

0 0 =   02

1 20

,    01       10

1            1            1                      1

г1 = г1 = ___'___„

2 %⁰ ’ ^{12     21}   2( %‘ — % ² )

,     11

—

( % — % )

, (35)

1                1

, Г 00 = Г 01

Г 10

Г 11

,    21       12

—

2 % — % )

, Г 0 2 = Г 20 =

¹     Г ¹²

0 ,    ²²

= % ^гтя.

1 ⁱ

Нелинейные связности находим по формулам (31а,в). Определим Гл ( % , п )

1 ⁱ

1 ⁱ

по формуле (31а) Г j ( % , п ) = Г jk ( % , п ) П . Имеем

п0

%0

—

( п^{1 —} п ²⁾    ,10 ₌

2 ( % — % ²) ’  '

—

п 0      Д0

2 ( %‘ — % ²) ^{,   2}

=     п0

2 % '- %' )

’     0

п1

2 % ⁰

Г 1 =

п °

2 %⁰

—

п          и

( %' — % )    2 ( % — % )

, Г 2

п1

2 ( % — % ) ’

Г 0

п2

2 %⁰  ’

1 Г 1 ²

—

п²            *2₌ п⁰

2 ( % — % ²) ’  ²   2 %

—

п1

2 %' — % ) + %

и2

—

ё) .

Эти функции действительно являются однородными функциями степени один в слоевых координатах.

1 ⁱ                                                                                                                      1   1 ⁱ

Связь величин G и Г jk ( % , п ) представляется формулой G ( % , п ) = - Г j ( % , п ) п ^j •

Эта формула играет здесь роль поверочной формулы. Подставив в эту формулу величины (34) и (36), получаем тождества. Значения величин (34) и (36), таким образом, найдены правильно.

Аналогично находятся коэффициенты нелинейных  связностей

2 пространства внутренних степеней свободы Γ ik ( 4 , Z ) .

2                           1 1

Для их нахождения можно использовать и формулу Г jk ( 4 , Z ) = Г jk ( 4 , Z ) С

Конкретные примеры. Определим абсолютный дифференциал составляющей вектора П

(универсальная газовая постоянная) по формуле (28)

1                          0      „

Зп ⁰ = d n° + J r d 4 -

1-^2              00

П п ) ЛЛ0      П Л1 п2

24^ d4 - 24^) d4 24^) d4, где dn0 = 0 (дифференциал от постоянной величины).

При изменении 4° (= ПМ на величину d4, 4 на величину d4, 42 на д4\1

величину d 4 ² , тогда п ( = —^)  изменится на величину Зц .

∂ τ

Универсальная газовая постоянная будет иметь новое значение, а именно,

R + Зп0

Аналогичные действия проводятся с постоянными С_р и С_р .

Заключение. Посредством геометрий расслоенного пространства, получили уравнения, которые совпадают по форме с основным уравнением ОТО и сохраняют основные его физико-геометрические связи. Показано, что данные уравнения, как и основное уравнение ОТО, основу которых составляет, по крайней мере, первый тензор кривизны Картана, формулы для потенциала и напряженности для гравитационного поля, закон Ньютона, формулы для потенциала и напряженности электростатического поля, закон Кулона образуют единую систему с единой физикогеометрической связью. Только форма реализации этой связи различная.

Введением соответствующих постоянных дважды свернутый тензор кривизны (типа тензора Риччи в римановой геометрии) может иметь размерность 1/ м², моль и др . Выбор размерности зависит от целей практических задач.

Объектом описания геометриями расслоенных пространств внутренних степеней свободы, таким образом, является релятивистская механика. Возможно описание и нерелятивистской механики, но в этом случае механические системы должны быть анизотропные, неоднородные и нелинейные. Данному описанию подлежат и анизотропные, неоднородные и нелинейные электромагнитные системы и процессы, тепловые нелинейные процессы, реальные газы и др., процессы пересечения: механико-электрические, механико-магнитные, термоэлектрические, термо-магнитные и др. Чтобы получать практически значимые результаты, метрические функции должны строится на основе экспериментальных данных.