Meta-Learning Enhanced BiLSTM Autoencoder with Channel-adaptive Quantization for Robust One-Bit Error Correction Coding

One-bit quantization has emerged as a vital technique in wireless communication, providing sizable reductions in hardware complexity and power consumption. One-bit quantization introduces considerable challenges in error correction, particularly when operating under diverse channel conditions such as Rician, Rayleigh, and additive white Gaussian noise (AWGN) environments. Conventional error correction codes often strive to adapt dynamically to varying channel characteristics without thorough retraining or prior knowledge of channel statistics [1]. The previous research approaches are often hindered by the "curse of dimensionality", but they explored the application of neural networks to develop decoding algorithms. The neural network learns a structured decoding algorithm rather than classifying codewords. However, the network is unattainable for practical block lengths. The one-bit systems cause the complete loss of amplitude information, apart from lowering measurements to sign constraints only [2].

Deep learning-based methods confirm the capability of autoencoder-based architectures for error correction coding [1]. One method could be to create a concatenated code by integrating the outer code (e.g., turbo or LDPC) with an inner code implemented by a trained autoencoder. In this hybrid model, the conventional code acts as an implicit regularizer [3]. The non-differentiable nature of the one-bit quantizer requires the autoencoder's training process based on this code [4]. Long short-term memory (LSTM) networks model sequential data and capture temporal dependencies in communication signals. Prior work explored LSTM-based autoencoders for one-bit quantization, achieving notable improvements over conventional coding methods over AWGN channels [3]. However, these approaches typically lack the adaptability required for robust performance across different highly dynamic fading channels [5]. Some approaches enable high-order modulation formats to be viable despite the presence of one-bit ADCs. A key insight is that the trained autoencoder provides approximately Gaussian distributed data to the conventional decoder [4]. This enables the standard decoder to function effectively in the presence of a non-Gaussian statistical received signal. Furthermore, the autoencoder can efficiently utilize excess bandwidth from pulse shaping. It maintains bandwidth efficiency while enhancing error correction capabilities [6].

Meta-learning, or “learning to learn,” offers a promising approach to address this limitation. It enables models to adapt to new tasks with minimal additional training in a rapid manner. It has been successfully applied in diverse domains, including few-shot learning and reinforcement learning [7]. Meta-learning can assist the development of channel-adaptive error correction schemes that generalize across diverse environments. Latest studies have investigated meta-learning for channel estimation and signal detection, but its integration with one-bit quantization error correction is still unexplored [8].

We propose a novel meta-learning-based BiLSTM autoencoder that continuously adapts its error correction based on channel conditions. The novelty derives from the integration of a meta-discriminator, which can learn channel-specific decision boundaries and modulate the adversarial loss during training. This novel approach enables the system to adapt to Rician, Rayleigh, and AWGN channels without requiring full retraining. Unlike current methods that depend on fixed quantization thresholds or assume known channel statistics, the proposed method learns to infer channel characteristics from the received signal and optimizes the error correction process accordingly.

The central contributions of this work are threefold:

• •    We present a meta-learning-driven LSTM autoencoder that co-optimizes for quantization efficiency and error correction across multiple channel types.

• •    We devise a channel-adaptive meta-discriminator that refines its decision boundaries through gradient-based updates, enabling dynamic adaptation to unseen channel conditions.

• •    We demonstrate through extensive experiments that the proposed framework achieves superior bit error rate (BER) and mean squared error (MSE) performance compared to existing methods, specifically in scenarios with limited training data or fast-changing channel characteristics.

2.    Related Works

• 2.1.    One-Bit Quantization in Communication Systems

• 2.2.    Deep Learning for Error Correction Coding

• 2.3.    Meta-Learning in Communication Systems

In Section 2, we discuss the one-bit quantization, the LSTM based autoencoders, and the meta-learning of the communication systems. Section 3 explains one-bit quantization and meta-learning principles. Section 4 provides fundamentals on autoencoder. Section 5 presents the proposed LSTM autoencoder architecture with meta-learning. Section 6 presents the results and comparisons with some baselines. Referring to the implications and future directions of research outlined in Section 7, the paper concludes in Section 8.

The field of error correction has traditionally relied on structured codes, such as convolutional codes (CCs) and polar codes, which present significant challenges in decoding complexity. A recent paradigm shift involves applying deep learning to this domain, where a deep neural network (DNN) is trained to act as a "one-shot" decoder. Research has shown that for short, structured codes, a DNN can achieve maximum a posteriori (MAP) performance and can generalize to decode codewords it has not seen during training, suggesting it learns a form of decoding algorithm rather than a straightforward classification mapping. This learning-based approach has also been successfully applied in an end-to-end manner for OFDM systems, where a DNN implicitly learns to handle channel distortion to recover transmitted symbols directly [4], [9], [10].

A parallel trend in machine learning and signal processing is model quantization, which reduces memory and energy consumption by representing network parameters using a small number of bits. The extreme of this is 1-bit quantization, where values are expressed as binary numbers. 1-bit compressive sensing-base literature demonstrated that accurate signal recovery is possible even when measurements are quantized to a single bit. It also addresses the problem of "sign flips" in the 1-bit measurements, which is analogous to bit errors in a channel. A robust adaptive outlier pursuit was proposed to detect the positions of these flips and considered the corrected measurements for signal recovery [11], [12].

Instead of handcrafting codes, a learning-based approach uses neural networks to learn both the encoding and decoding functions. It applies to complex non-linear computations where traditional codes fail. Other approaches combined cryptography and channel coding to utilize the cryptographic message digest as redundancy for forward error correction. In this method, reliability values (L-values) from the channel decoder are used as feedback to correct bits. This method provides a coding gain over conventional methods [13], [14].

One-bit quantization reduces hardware complexity while retaining reasonable signal fidelity. Existing literature examined its applications in diverse communication scenarios, such as massive MIMO systems [15] and underwater optical communications [16]. These studies underscore the trade-off between quantization noise and computational efficiency in bandwidth-constrained environments. Traditional approaches generally rely on fixed quantization thresholds, which may not adapt well to varying SNR values or channel fading conditions. Current efforts introduced learnable quantization thresholds [1], presupposing static channel characteristics during training.

Deep learning-based autoencoders have become a compelling alternative to traditional error correction codes in complex or time-varying channel scenarios. Previous research confirmed the viability of using MLPs and CNNs for encoding and decoding [17]. Lately, recurrent architectures such as LSTMs have shown superior performance in capturing temporal dependencies [18]. However, these approaches generally prioritize on full-precision signal representations and do not explicitly address the challenges of extreme quantization. Hybrid methods combining autoencoders with generative adversarial networks (GANs) have been proposed to mitigate quantization noise [16], but they are deficient in mechanisms for channel adaptation.

Meta-learning has been utilized for diverse communication problems, including channel estimation and adaptive filtering [19]. These techniques facilitate quick adaptation to new environments by learning shared representations across tasks. In adversarial settings, meta-learning has been employed to enhance robustness against jamming and interference [20]. Federated meta-learning frameworks have also been investigated for privacy-preserving adaptation in satellite networks [21]. However, existing meta-learning approaches in communications mainly concentrate on signal processing tasks rather than error correction coding under one-bit quantization constraints.

• 2.4.    Adversarial Training for Robustness

3.    Background on One-Bit Quantization and Meta-Learning

• 3.1.    One-Bit Quantization Principles

Adversarial training has been extensively implemented to enhance model robustness against input perturbations. In communication systems, it has been applied to enhance resilience against channel-aware adversaries [22]. These techniques commonly utilize a static discriminator that remains fixed during inference, limiting their ability to adapt to dynamic channel conditions. Recent research has sought to optimize meta-learning algorithms for vehicular communications through adversarial training [8], but these methods fail to account for the specific challenges of one-bit quantization.

Our proposed method diverges from existing approaches in several key aspects. First, unlike conventional one-bit quantization methods with fixed thresholds, our framework co-optimizes quantization and error correction through a learnable LSTM autoencoder. Second, in contrast to conventional adversarial training techniques, our meta-discriminator dynamically adjusts its decision boundaries based on real-time channel statistics, allowing for adaptation without retraining. Third, while prior meta-learning applications in communications focus on signal processing tasks, our research focuses directly on error correction under extreme quantization, addressing a critical gap in the literature. This combination of adaptive quantization, meta-learning, and adversarial training provides a unified solution for robust communication in dynamic environments.

To establish the theoretical foundation for our proposed method, we begin by outlining the core concepts in one-bit quantization and meta-learning. These two domains offer complementary advantages for addressing the challenges of robust error correction in dynamic channel environments.

One-bit quantization represents an extreme case of analog-to-digital conversion where continuous-valued signals are mapped to binary values { - 1, + 1 } . The quantization process can be formulated as:

y = sign ( x - т )                                                ⁽¹⁾

where x denotes the input signal, т is a quantization threshold, and sign ( • ) is the signum function. This process inherently involves quantization noise, whose characteristics depend on both the input signal distribution and the choice of т [23]. The reconstruction error worsens significantly when the input signal has high dynamic range or when channel impairments distort the quantized values.

Conventional techniques commonly utilize fixed thresholds based on signal statistics [24], but these may perform poorly under time-varying channel conditions. Recent studies have investigated adaptive thresholding schemes where т is learned from data [25]. However, these methods typically require retraining when channel characteristics change significantly.

• 3.2.    Meta-Learning Fundamentals

Meta-learning aims to develop models that can quickly adapt to new tasks with minimal additional training. The core principle is based on learning across multiple related tasks to acquire transferable knowledge that facilitates fast adaptation [26]. In light of communication systems, each task could correspond to a different channel condition or SNR level.

In meta-training, a model learns by tackling a series of tasks. For each task T _i sampled from a distribution p (T ), the model f is first trained on a small set of K samples using the task-specific loss function L_T . Next, the model is evaluated on new, unseen data from the same task. The model's parameters are then updated based on its performance on this test data. This test error on individual tasks serves the purpose of the training error for the overall meta-learning process. Once meta-training is complete, the model's final performance is measured on entirely new tasks that were held out during training. This evaluation assesses how well the model can learn and adapt when presented with just K samples from a novel task.

A meta-learning approach optimizes model parameters 0 such that a small number of gradient updates on a new task yields good performance:

0 = arg min У Ц ( f_e ,)                               (2)

0   "  ■'

T ~ p ( T )

where О = 0 - a V ₀ L_T ( f ₀ ) represents the adapted parameters, a is the step size, and p ( T ) is the task distribution. This formulation enables the model to leverage prior experience when confronted with new but related scenarios [7].

• 3.3.    Challenges in Combining Both Domains

4.    Autoencoder Fundamentals

• 4.1.    LSTM-Based Autoencoder

Integrating one-bit quantization with meta-learning introduces distinct difficulties. The non-differentiability of the signum function complicates gradient-based optimization, requiring surrogate gradient methods during training [27]. Additionally, the extreme information loss from quantization hinders the process of extracting sufficient features for channel adaptation. Previous initiatives aimed at addressing these issues have either focused on full-precision metalearning [28] or non-adaptive quantization [6], but not their combination.

The interaction between quantization noise and channel noise further compounds the problem. While conventional error correction codes usually handle these noise sources separately, our framework must jointly model their effects to achieve robust performance. This warrants careful design of the meta-learning objective to account for both quantization-induced distortion and channel impairments.

The primary gameplay of an autoencoder involves encoding data using the encoder and decoding it using the decoder. The encoder converts an input message into a codeword. In turn, we can obtain the codeword from the information at the encoder. The primary goal is to train the parameters of the encoder and decoder functions, resulting in a minimal reconstruction error between the input and output. By back-propagation and gradient descent methods, we can achieve this by minimizing a loss function (negative log-likelihood).

Long Short-Term Memory (LSTM) cells manage the flow of information through a system of gates. These gates allow LSTMs to regulate data effectively during the training process. In the cell, the functional relationship for each component is given as follows:

i_t f t c_t o_t

a

ft □ c_t - 1 + i_t □ tanh

W a?

t ht-1

+ b e

h t = o tQ tanh ( ^ct )

The LSTM neuron consists of an input gate an input gate ( i_t ) , a forget gate ( f t ) , a cell ( c_t ) , an output gate ( o_t ) , and an output response ( h_t ) . The input gate and forget gate govern the information flow into and out of the cell. The output gate regulates the amount of information from the cell that is passed to the output. h_t - 1 and X_t represent a prior hidden state and a current input. W _a p denotes the weight matrix between a e { x , h , c } and в e { i , f , c , o } whereas b p denotes the bias in terms of p e { i , f , c , o } . The symbol a represents a nonlinear activation function, and the symbol 0 denotes the element-wise product.

• 4.2.    BiLSTM-based Autoencoder

• 4.3.    One-Bit Quantized BiLSTM Autoencoder

A Bidirectional LSTM (BiLSTM) works by simultaneously processing streams of data in both forward and backward directions. At each time step, forward and backward LSTM networks are fed the input state to capture both future and past context. This two-way approach enables students to learn more effectively and efficiently. X_t - 1 , X_t , and X_{t + 1} are the previous, present, and future inputs, respectively. Y_t - 1 , Y_t , and Y_{t + 1} are the previous, present, and future outputs, respectively. The BiLSTM architecture is shown in Figure 1.

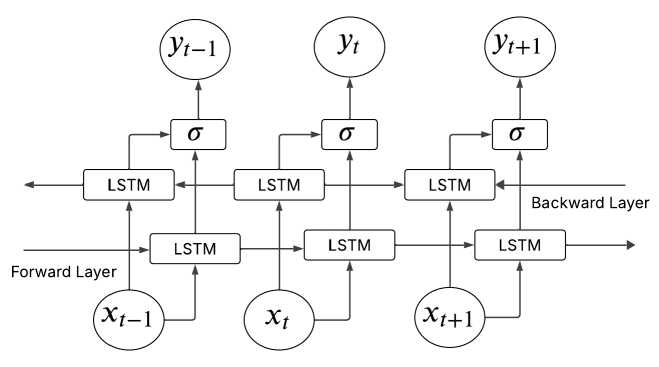
Fig.1. BiLSTM architecture

This architecture treats the autoencoder as a communication channel to address the adverse effects of quantization. The process is as follows:

• •    Input Encoding: A message is first converted into a one-hot encoded vector.

• •    Transmission and Noise: This vector is passed through the encoder, which yields a codeword. The signal is then subjected to noise in the channel.

• •    Quantization: A one-bit quantization function is applied element-wise to the received signal.

• •    Decoding: The resulting quantized signal is processed by the decoder, which uses an activation function to

produce the final output probability vector.

• •    Training: Minimizing the cross-entropy function between the input and output layers trains the encoder and decoder parameters.

5.    Meta-Learning-driven BiLSTM Autoencoder for Robust One-Bit Quantization Error Correction

• 5.1.    Applying Meta-Learning to One-Bit Quantization Error Correction in BiLSTM Autoencoder

The proposed method integrates meta-learning with a BiLSTM-based autoencoder to achieve robust error correction across diverse channel conditions. This method consists of three components: a bidirectional LSTM encoder-decoder, a learnable one-bit quantizer with adaptive thresholds, and a channel-aware meta-discriminator. These components optimize both quantization efficiency and error correction performance while retaining adaptability to varying channel characteristics.

The meta-learning framework follows a dual-phase optimization process. In the inner loop, the system adapts to specific channel by minimizing a task-specific loss function. The outer loop then updates the meta-parameters to improve generalization across diverse channels. This method adapts to its error correction strategy when encountering new channel conditions. The BiLSTM encoder captures both forward and backward temporal dependencies by processing the input signal x through bidirectional layers:

h = LSTM fwd ( x t , h f w d )                                         (5)

h b^wd = LSTM_b wd ( x _t , h Jw^d )                                       (6)

Where the forward and backward hidden states at the time step t are represented by h _t ^fwd and h _t ^bwd . The encoder output combines these states through a residual connection:

z t = W e [ h fwd ; h b^wd ] + x _t                                         (7)

Here, W _e denotes a learnable weight matrix that projects the concatenated hidden states to the latent space dimension. The residual connection preserves the original signal information while enabling the network to learn incremental corrections.

• 5.2.    Key Components of the Meta-Learning-Driven System

The learnable quantizer Q implements adaptive thresholding through trainable parameters τ that adjust based on channel conditions:

Q (z ) = sign (z - т)

The thresholds τ are optimized jointly with other network parameters during meta-training. This contrasts with prior methods where thresholds remain fixed during inference. The quantized signal y = Q ( z ) then passes through the channel, experiencing impairments modeled as additive noise n :

y ' = y + n

The meta-discriminator fl _meta processes the received signal y ' to estimate channel characteristics. Its architecture employs cross-attention mechanisms to compute channel embeddings using vectors of queries, keys, and values:

c = CrossAttention (y', Wkey y', Wval y')

These embeddings condition the discriminator’s decision boundaries, enabling channel-specific adaptation. The adversarial loss Ladv incorporates these dynamic boundaries:

Ladv = E [logOmeta (X)]+E[ log(1 — ^meta (G(у')))]

where G represents the decoder function. D _meta ( x ) is the output of the meta-discriminator when given real data from x whereas D ( G ( y ' ) ) is the output of the discriminator when given fake generated data. Maximizing log ( 1 - D ( G ( y ' ) ) ) correctly labels the fake data coming from the generator. The total loss combines reconstruction error, adversarial loss, and meta-regularization:

L t _o t _al = 4 Dx - Xo2 + 4 L _a dv + 4 DV _e L _a dvD2                             (12)

The meta-regularization term □ V_e L _adv D2 stabilizes the adaptation process by preventing excessive parameter updates that could lead to instability. 4 1 , 4 2 , and 4 3 are the hyperparameters. The proposed framework is shown in Figure 2.

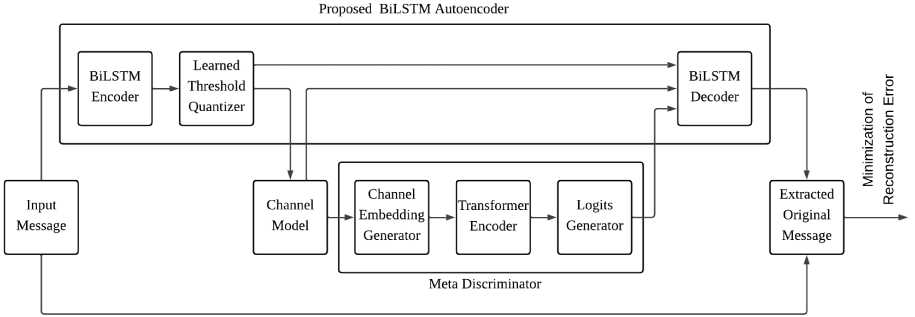
Fig.2. Proposed BiLSTM autoencoder with meta-discriminator for one-bit quantization error correction

• 5.3.    Real-Time Adaptation to Unseen Channels

During inference, the system adapts to new channel conditions through a single gradient step. The adaptation process uses the current received signal to compute channel-specific updates:

0 ' = 0 - « V ₀ L adapt ( y ' )

where L _adapt represents the adaptation loss computed on a small batch of received symbols. This efficient update mechanism allows the system to sustain performance even when channel statistics deviate from those encountered during training.

The decoder architecture mirrors the encoder’s bidirectional structure but incorporates the channel embeddings c from the meta-discriminator:

hfd = LSTMfwd ([y'; c], hf-wd)

hˆbwd t = LSTMbwd ([yt;c],ht+1 )

The final reconstruction combines the decoder outputs with the quantized values through another residual connection:

xt = W, [ht  ;hbwd] + yt(16)

where W _d projects the concatenated hidden states back to the input dimension.

Algorithms 1 and 2 explain the meta-training for adaptability, and inference and real-time adaptation, respectively.

Algorithm 1 Meta-Training for Adaptability

Input: Distribution of channel conditions p ( T ), learning rates а , в

Output: Optimized meta-parameters 0

• 1:    Initialize parameters 0 (for Encoder, Decoder, and Meta-Discriminator)

• 2:    for number of training iterations do

• 3:  // Outer Loop (Meta-Optimization)

• 4:   Sample a batch of tasks { T } ~ p ( T )

• 5:   Initialize meta-loss L _meta ^ 0

• 6:   for each sampled task T do

• 7:     // Inner Loop (Task-Specific Adaptation)

• 8:     Sample support dataset D _supp (passed through channel T )

• 9:      Calculate task-specific adversarial loss L _adv( 0 ) on D _supp

• 10:     Compute hypothetical update: ff i ^ 0 - aV₀ L _adv ( 0 )

• 11:     // Evaluate Adapted Parameters

• 12:     Sample query dataset D _query (passed through channel T_i )

• 13:      Calculate total loss L _total( 0 / ) using 0' i on D _query

• 1^4:     Accumulate meta-loss: L meta ^ L meta + ^L total ^{( 0}' i )

• 15:   end for

• 16:  // Outer Loop Update (Meta-Parameter Update)

• 17:  Update meta-parameters: 0 ^ 0 - PV₀ L _meta

• 18:    end for

• 19:    return 0

Algorithm 2 Inference and Real-Time Adaptation

Input: Pre-trained meta-parameters 0 from Algorithm 1, adaptation learning rate а

Output: Adaptation of the trained meta-parameters 0 to the current channel conditions for optimal performance

• 1:    // Adaptation Phase

• 2:    Receive small initial batch of symbols y_adaptfrom the new channel

• 3:    Calculate adaptation loss L_adapton y_adapt

• 4:    Perform single, real gradient update: θ′ ←θ-α∇_θL_adapt(y_a′_dapt)

• 5:    // Steady-State Operation

• 6:    Use the adapted model with parameters θ′ for encoding and decoding of all subsequent data

• 7:    // Repeat adaptation process (lines 2-4) for the changing channel statistics

• 5.4.    Unified Handling of Diverse Channels

6.    Experiments 6.1.    Experimental Setup

• 6.2.    Performance Metrics

The system’s ability to generalize across different channel types derives from its meta-learning formulation. During training, the model is presented with samples from Rician, Rayleigh, and AWGN channels, learning to extract channelinvariant features while maintaining the flexibility to adapt to specific conditions. The meta-discriminator’s attention mechanism plays a central role in this process by identifying salient features that distinguish between channel types. The cross-attention weights in (10) reveal which aspects of the received signal contain the most information about channel characteristics. These attention patterns evolve during meta-training to focus on features that best support adaptation. For example, in Rician channels, the attention might emphasize the dominant line-of-sight component, while in Rayleigh channels, it could focus on statistical properties of the fading envelope.

The unified technique outperforms channel-specific models. First, it reduces memory requirements by eliminating the need to store separate models for different channel types. Second, it enables seamless transitions between channel conditions without explicit switching mechanisms. Third, it provides robustness against channel estimation errors by learning to deduce characteristics directly from the received signal. The complete system operates as an end-to-end trainable architecture where all components such as encoder, quantizer, meta-discriminator, and decoder are optimized jointly through the meta-learning objective. This holistic optimization ensures that each component promotes the achievement of the overall aim of robust error correction under one-bit quantization constraints.

To evaluate the proposed meta-learning-driven LSTM autoencoder, we performed a comprehensive set of experiments under three channel conditions: Rician (K-factor = 10 dB), Rayleigh fading, and AWGN. The system was implemented using Python (PyCharm 2020.3) with the following configurations: bidirectional LSTM layers (128 hidden units each), meta-discriminator with 4 attention heads, and Adam optimizer (learning rate = 0.001). Training utilized a meta-batch size of 32 tasks, where each task corresponded to a different channel realization. All models were trained until convergence on the same dataset of 100,000 symbol sequences (QPSK modulated, length=64).

To quantitatively evaluate system performance, two key metrics are employed: Bit Error Rate (BER) and Mean Squared Error (MSE).

• •    The BER is the probability of error of a transmission scheme. The BER is defined as the number of bit errors divided by the total number of bits transmitted during a given time interval. A low bit error rate shows a reliable and accurate link.

• •    The MSE at the receiver represents the extent to which the prediction deviates from the sample or observed values. The MSE is a standard metric used to evaluate the performance of channel estimation. The receiver makes precise adjustments for the channel's distortion if the MSE is low.

• 6.3.    Results and Analysis

  The experimental setup provides a comparative analysis of the proposed method against four state-of-the-art (SOTA) methods: Deep Learning-based Quantization (DLQ) [1], Deep Reinforcement Learning-based Federated Learning Quantization (DRL-FLQ) [25], Low-Density Parity-Check with Adaptive Equalization (LDPC-AEQ) [29], and Probabilistic Adaptive Coded Quantization (PACQ) [9]. In DLQ, the Turbo code acts as an implicit regularizer for the AE, which is hard to train due to one-bit quantization. The AE provides Gaussian-distributed data to the Turbo decoder. The DRL-FLQ method is designed for model compression to reduce communication traffic in federated learning (FL) systems. The LDPC-AEQ method is intended for robust error correction coding to overcome the severe non-linearity of a one-bit ADC in a communication channel. In PACQ, the Fano decoder's bias is set to the bit-channel cutoff rate. This maintains superior error-correction performance while achieving lower computational complexity. The evaluation is performed over simulated Rician, Rayleigh, and AWGN fading channels. The main aim is to evaluate the proposed method as compared to SOTA methods by examining their BER and MSE as a function of increasing data size from 500 to 2500 symbols.

• A.    Comparative Evaluation of Meta-learning Driven LSTM autoencoder Over Rician Fading Channel

The Rician fading channel provides a stochastic representation for a channel where a dominant, non-fading signal component is added with weaker and scattered components. The main element is a direct Line-of-Sight (LOS) path between the transmitter and receiver. These conditions arise in many practical wireless scenarios, including indoor wireless LANs, microcellular systems, satellite links, and vehicle-to-vehicle (V2V) communication networks.

The Rician channel is mathematically characterized by the Rician K-factor, which is defined as the ratio of the signal power in the dominant path to the total power in the other scattered paths. A large K-factor signifies a strong LOS component, making the channel less severe than a Rayleigh fading environment, which models non-LOS conditions. The performance of any communication protocol in a Rician channel is therefore highly reliant on its ability to leverage the stability of the LOS component while effectively mitigating the interference from the diffuse multipath components. The comparative BER and MSE performance of the proposed method and the four SOTA methods are detailed in Figure 3 and Table 1.

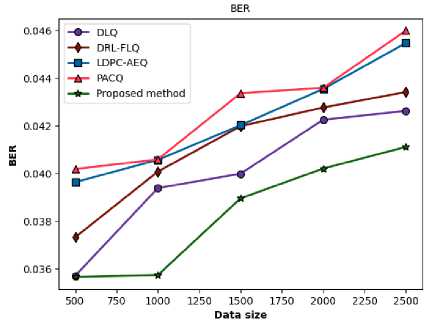
The evidence suggests that the proposed approach outperforms others for all data sizes. The proposed method has the lowest BER among the three techniques at all measurement points. For example, when the data size is 500, the BER for the proposed method is 0.027472, which is 7.96% better than the next best alternative, DLQ (0.029846), and 18.56% better than the worst one, PACQ (0.033733). As the data expands, this performance ease continues to hold, revealing the steady and durable nature of the proposed method.

The proposed method begins with a moderate increase; its degradation rate becomes notably more stable and lower than that of its main competitor, DLQ, at larger packet sizes. In the transition from a data size of 1500 to 2000, the BER of the proposed method increases by only 2.95%, whereas DLQ's BER jumps by 5.98%. Similarly, from 2000 to 2500, the proposed method's degradation is 3.66% compared to DLQ's 7.43%.

The method's superior stability indicates a more robust system for handling the time-varying nature of the channel. It is inherently more resistant to the effects of stale CSI. This robustness yields a real-world advantage for applications in highly dynamic Rician environments. In line with the BER results, the proposed method attains the lowest MSE values across all data sizes, indicating superior fidelity in signal estimation.

A lower MSE suggests that the receiver is more effective at mitigating the channel's effects, resulting in a more precise and detailed portrayal of the transmitted signal. Combating channel-induced noise, distortion, and interference is fundamental to the overall performance of the method. For example, at a data size of 2500 symbols, the proposed method's MSE of 0.031034 is 1.76% lower than DLQ's and 13.78% lower than PACQ's, illustrating its persistent advantage in estimation accuracy.

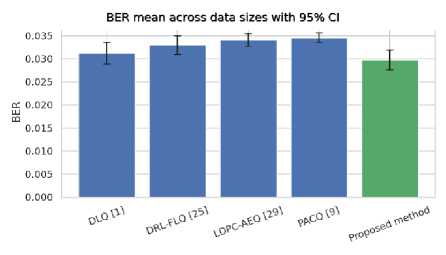
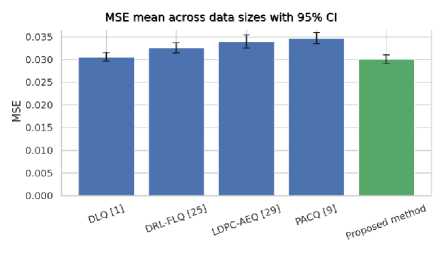
BER and MSE mean values across data sizes, with 95% confidence interval (CI) error bars, over a Rician fading channel, are shown in Figs. 4(a) and 4(b). The proposed method exhibits the lowest mean BER of 0.02974, with clear, non-overlapping 95% CI (0.02760 (lower) to 0.03188 (upper)), compared to LDPC-AEQ [29] and PACQ [9]. DLQ [1] and DRL-FLQ [25] are closer, with overlapping CIs, but still have a higher mean BER. The proposed method shows the lowest mean MSE of 0.03 with a non-overlapping 95% CI (0.029152 (lower) to 0.031038 (upper)) compared to DRL-FLQ [25], LDPC-AEQ [29], and PACQ [9]. DQ [1] is close and overlaps, but the proposed method remains lower in terms of the MSE mean.

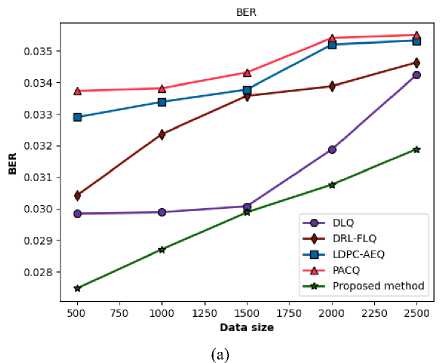
Fig.3. Comparative performance of the proposed method over a Rician fading channel in terms of (a) BER versus data size in symbols and (b) MSE versus data size in symbols

(b)

Table 1. Comparative evaluation of BER and MSE versus data size of the proposed method with other methods over a Rician fading Channel

BER versus data size over a Rician fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.029846	0.030415	0.032894	0.033733	0.027472
1000	0.029885	0.032363	0.033384	0.033816	0.028711
1500	0.030074	0.033573	0.033776	0.034313	0.029883
2000	0.031873	0.03388	0.0352	0.035405	0.030763
2500	0.03424	0.034635	0.035326	0.035501	0.031888
MSE versus data size over a Rician fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.029728	0.031647	0.032915	0.033714	0.029317
1000	0.030192	0.032152	0.033388	0.034036	0.029384
1500	0.030275	0.032335	0.033761	0.034383	0.030086
2000	0.031202	0.032733	0.0338	0.035464	0.030655
2500	0.031591	0.034024	0.035989	0.035993	0.031034

(a)                                                                          (b)

Fig.4. (a, b) BER and MSE means across data sizes with 95% confidence interval (CI) error bars over a Rician fading channel

• B.    Comparative Evaluation of Meta-learning Driven LSTM Autoencoder Over Rayleigh Fading Channel

The Rayleigh fading channel is characteristic of scenarios with no direct Line-of-Sight (LOS) path between the transmitter and receiver, such as in densely populated urban areas, where buildings and other obstructions scatter the signal extensively. The received signal is therefore a complex summation of numerous weaker, scattered components.

(a)

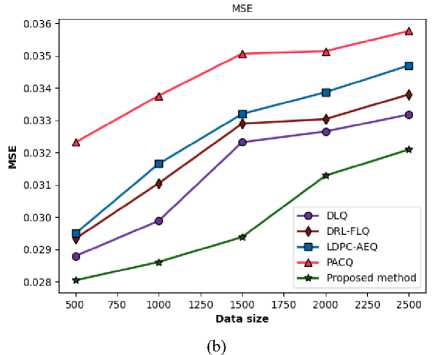
Fig.5. Comparative performance of the proposed method over a Rayleigh fading channel in terms of (a) BER versus data size in symbols and (b) MSE versus data size in symbols

The Rayleigh fading model is often considered a special case of the more general Rician fading model. When the Rician K-factor, the ratio of power in a dominant path to the power in scattered paths, approaches zero, the Rician distribution converges to a Rayleigh distribution, representing the most severe fading conditions where the receiver can leverage no stable LOS path. The performance of any communication protocol in a Rayleigh channel is therefore crucially contingent upon its ability to operate reliably in the complete absence of a dominant signal component, effectively mitigating the severe interference from the diffuse multipath components.

A communication system's effectiveness is defined by its ability to reliably deliver data with minimal errors, particularly in a challenging NLOS environment. The comparative BER performance of the proposed method and the four benchmark schemes is detailed in Fig. 5 and Table 2.

Table 2. Comparative evaluation of BER and MSE versus data size of the proposed method with other methods over a rayleigh fading channel

BER versus data size over a Rayleigh fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.035701	0.037316	0.039631	0.040181	0.035652
1000	0.039381	0.040074	0.040568	0.040586	0.03573
1500	0.039987	0.041981	0.042022	0.043364	0.038951
2000	0.042254	0.042766	0.043545	0.043592	0.040203
2500	0.042622	0.043416	0.04547	0.045994	0.041111
MSE versus data size over a Rayleigh fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.028797	0.029336	0.029495	0.032321	0.028045
1000	0.02989	0.031054	0.031657	0.033767	0.028616
1500	0.032327	0.032903	0.033201	0.035069	0.029387
2000	0.032658	0.033043	0.033874	0.035145	0.031289
2500	0.033186	0.033806	0.034704	0.035772	0.032098

The data proves the proposed method's superior performance across all evaluated data sizes in the Rayleigh channel. At every measurement point, the proposed method achieves the lowest BER, signifying higher data fidelity and system reliability. For the smallest data size of 500, the proposed method's BER of 0.035652 is marginally better than DLQ (0.035701) but represents a substantial 11.27% improvement over the weakest performer, PACQ (0.040181). The method's superior performance becomes increasingly significant as the data size increases, highlighting the consistent and robust nature of the proposed scheme in a severe fading environment.

The proposed method maintained a high degree of constancy during the initial transition from a 500 to 1000 data size, with a negligible degradation of only 0.22%, significantly outperforming all competitors. Notwithstanding a significant elevation of 9.01% in the next step, its degradation rate stabilizes significantly for larger packet sizes, with increases of only 3.21% and 2.26% in the final two transitions. In contrast, methods such as PACQ and LDPC-AEQ exhibit high degradation rates at the largest packet sizes (5.51% and 4.42%, respectively).

This pattern suggests a highly sophisticated mechanism for handling the time-varying nature of the channel. Its ability to maintain a low and stable rate of degradation at larger data sizes is a significant practical advantage. It exhibits built-in robustness against the effects of stale CSI, making it a more reliable choice for applications that require the transmission of large data sizes in dynamic NLOS environments.

Consistent with the BER results, the proposed method achieves the lowest MSE across all data sizes, indicating superior fidelity in signal estimation. A lower MSE suggests that the receiver is more effective at mitigating the channel's effects, delivering a higher-fidelity and less biased representation of the transmitted signal. This superior capability in combating channel-induced noise, distortion, and interference is fundamental to its overall performance. For example, at a data size of 2500, the proposed method's MSE of 0.032098 is 3.28% lower than DLQ's and 10.27% lower than PACQ's, demonstrating its sustained advantage in estimation accuracy.

(a)                                                                              (b)

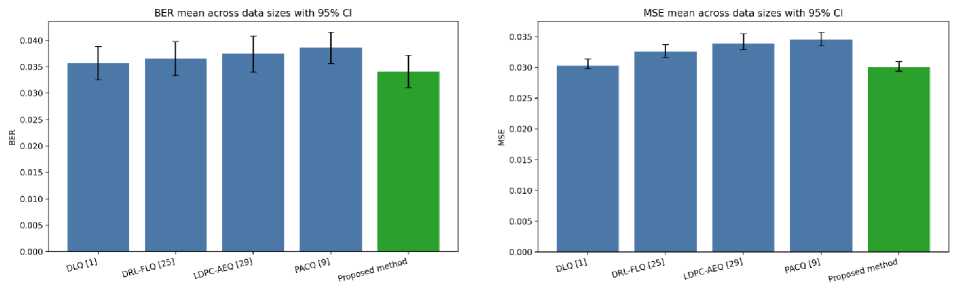
Fig.6. (a, b) BER and MSE means across data sizes with 95% confidence interval (CI) error bars over a Rayleigh fading channel

BER and MSE mean values across data sizes, with 95% confidence interval (CI) error bars, over a Rayleigh fading channel, are shown in Figs. 6(a) and 6(b). The proposed method exhibits the lowest mean BER of 0.0341 with 95% CI (0.03107 (lower) to 0.03714 (upper)) compared to the competing methods, which have increasing mean BERs, i.e., DLQ [1] < DRL-FLQ [25] < LDPC-AEQ [29] < PACQ [9]. In Fig. 6(a), gaps are small to moderate, and CI overlaps exist with top baselines. In Fig. 6(b), the proposed method exhibits overlapping mean MSE with DLQ [1], but it achieves the lowest mean MSE of 0.03 with 95% CI (0.0294 (lower) to 0.0310 (upper)) among competing methods, which have increasing mean MSE, i.e., DRL-FLQ [25] < LDPC-AEQ [29] < PACQ [9]. The proposed shows non-overlapping Cis with LDPC-AEQ [29] and PACQ [9].

• C.    Comparative Evaluation of Meta-learning Driven LSTM Autoencoder Over AWGN Fading Channel

The AWGN channel represents the effect of random, wideband noise that is statistically characterized as a Gaussian process. The term "additive" signifies that the noise is superimposed onto the signal, while "white" implies that its power is uniformly distributed across all frequencies in the communication band. Unlike fading channels, the AWGN channel is static; it does not introduce time-varying fluctuations in signal amplitude or phase. Therefore, performance in an AWGN channel is a direct measure of a system's robustness to random noise. The comparative BER performance of the proposed method and the four benchmark schemes in an AWGN channel is detailed in Figure 7 and Table 3.

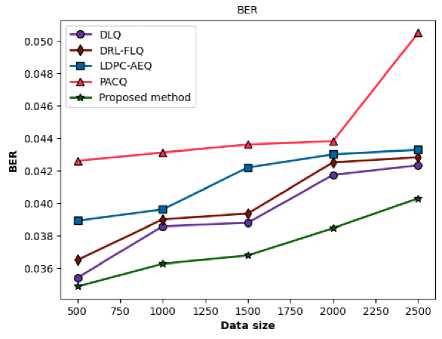
(a)

Fig.7. Comparative performance of the proposed method over an AWGN fading channel in terms of (a) BER versus data size in symbols and (b) MSE versus data size in symbols

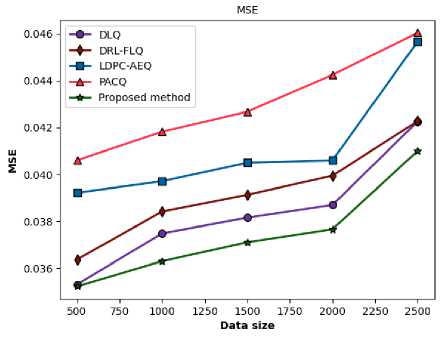
(b)

The data provides compelling evidence of the proposed method's superior performance across all evaluated data sizes. At every measurement point, the proposed method achieves the lowest BER, signifying higher data fidelity and system reliability. For instance, with a data size of 500 symbols, the proposed method's BER of 0.034878 represents a 1.5% improvement over the next-best performer, DLQ (0.035419), and a substantial 18.16% improvement over the weakest performer, PACQ (0.042618). The method's outperformance is maintained and increasingly evident as the data size increases, providing evidence for the reliability and resilience of the proposed method against Gaussian noise.

Table 3. Comparative evaluation of BER and MSE versus data size of the proposed method with other methods over an AWGN fading Channel

BER versus data size over an AWGN fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.035419	0.036506	0.038922	0.042618	0.034878
1000	0.038583	0.039006	0.039621	0.04313	0.036277
1500	0.038796	0.039368	0.042203	0.043615	0.036786
2000	0.041746	0.04252	0.043017	0.043826	0.038464
2500	0.04234	0.042838	0.043293	0.050498	0.040308
MSE versus data size over an AWGN fading Channel
Data size /Methods	DLQ [1]	DRL-FLQ [25]	LDPC-AEQ [29]	PACQ [9]	Proposed method
500	0.03531	0.036374	0.039217	0.040606	0.035225
1000	0.037487	0.038419	0.039714	0.041824	0.036305
1500	0.038159	0.039132	0.040501	0.042677	0.037108
2000	0.0387	0.039949	0.040598	0.044249	0.037663
2500	0.042261	0.042274	0.04567	0.046042	0.041003

Table 3 shows that all five approaches to BER degrade with the increase in data size. In an AWGN channel, this cannot happen unless it is due to something like fading and other time-varying channel effects. Longer data packets increase the statistical probability of encountering noise sequences that are especially demanding for the decoder. Furthermore, for adaptive algorithms or systems with memory, minor estimation errors can accumulate over a longer processing window, resulting in a gradual degradation of decoding performance.

While the proposed method yields a moderate, but sustained degradation rate, other methods exhibit more erratic behavior. For example, PACQ shows excellent stability for smaller transitions but suffers a catastrophic 15.22% degradation when moving from a 2000 to a 2500 data size. DLQ and DRL-FLQ also experience significant jumps in degradation (7.60% and 8.01%, respectively) in the 1500 to 2000 transition. The proposed method's relatively stable degradation profile implies a more stable and effective error-handling mechanism, which is highly beneficial for system design and performance prediction.

Consistent with the BER results, the proposed method achieves the lowest MSE across all data sizes, indicating superior fidelity in signal estimation. A lower MSE suggests that the receiver is more effective at mitigating the effects of noise, delivering a higher-fidelity representation of the transmitted signal. This superior capability in combating noise is fundamental to its overall performance. For example, at a data size of 2500 symbols, the proposed method's MSE of 0.041003 is 3.0% lower than DLQ's and 10.9% lower than PACQ's, demonstrating its sustained advantage in estimation accuracy.

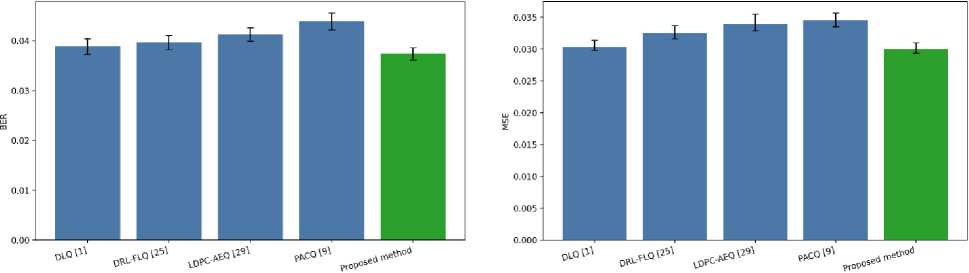
BER and MSE mean values across data sizes, with 95% confidence interval (CI) error bars, over a Rayleigh fading channel, are shown in Figs. 8(a) and 8(b). In Fig. 8(a), the proposed method has the lowest mean BER of 0.0374 with 95% CI (0.03615 (lower) to 0.03865 (upper)). The proposed method has a closer CI overlap with DLQ [1] and DRL-FLQ [25], but it does not have CI overlap with LDPC-AEQ [29] and PACQ [9]. In Fig. 8(b), the proposed method has the lowest mean MSE of 0.03 with 95% CI (0.0294 (lower) to 0.031(upper) ) compared to competing methods, DRL-FLQ [25], LDPC-AEQ [29], and PACQ [9] at the 95% CI level. The proposed method has a close CI overlap with DLQ [1].

BER mean across data sizes with 95% Cl                                                      MSE mean across data sizes with 95% Cl

(a)                                                                                (b)

Fig.8. (a, b) BER and MSE means across data sizes with 95% confidence interval (CI) error bars over an AWGN fading channel

• D.    Impact of Increasing Data Size on BER

One evident trend observed in Tables 1, 2, and 3 is that the BER of all five methods deteriorates as the data size increases. A receiver’s performance depends heavily on the availability of accurate CSI-Channel State Information, which provides information on how the signal is affected by the channel. This CSI is generally estimated at the beginning of a data packet. Wireless channels exhibit a coherence time, which refers to the duration during which the channel's response to an impulse remains effectively invariant. The relative motion of the transmitter and the receiver causes the Doppler spread, which is inversely proportional to the coherence time. A larger data packet requires a longer transmission time. If this transmission duration is larger than the coherence time of the channel, the first CSI estimate will become stale or outdated during the latter parts of the packet. The assumption of the channel state not matching the real channel state causes imperfect equalization and decoding, which increases the bit-error-probability. The increasing BER with data size for all methods is due to the coherence time bottleneck. Long packets experience significant changes in channels during transmission, which is why they show growing BER.

• E.    Core Performance Analysis

The proposed method consistently yields higher reliability, evidenced by lower BER and MSE values in all tested channel conditions. The analysis indicates a direct causal relationship between these two metrics: the method's excellent BER is a direct consequence of its outstanding MSE performance. Producing a more accurate estimate of the transmitted symbols (a low MSE) provides a cleaner, higher-fidelity signal to the decoder. This cleaner input reduces ambiguity in the decision-making process, which directly leads to a lower final BER. The proposed method shows the lowest BER of 0.027 and the lowest MSE of 0.028 in Rician and Rayleigh channels, respectively.

• F.    Influence of Data Packet Size

A consistent trend observed across all methods is that the MSE increases with larger data packet sizes. This degradation is attributed to the accumulation and propagation of minor estimation errors over the longer processing window of a large data packet. However, the proposed method exhibits greater robustness, as its MSE increases at a slower rate compared to the benchmarks. This suggests its underlying algorithms are less susceptible to this error propagation phenomenon, allowing it to sustain higher accuracy over extended periods.

• G.    Advantages of the Proposed Method

Based on its empirical performance, several architectural advantages of the proposed method can be inferred:

• •    Advanced Channel Dynamics Tracking: The method's robustness, especially in time-varying Rician and Rayleigh channels, implies it has a highly effective mechanism for tracking channel changes. It may leverage stable line-of-sight (LOS) components in Rician channels or effectively track rapidly changing non-line-of-sight (NLOS) Rayleigh channels. In the AWGN channel, this translates to superior noise mitigation and filtering capabilities.

• •    Joint Estimation and Decoding: The superior stability could stem from an iterative receiver architecture where channel estimation and data decoding are performed jointly rather than sequentially. The proposed method helps refine the channel estimate, creating a synergistic loop that suppresses error propagation.

• •    Resilient Signal Representation: The proposed method is inherently more resilient to the statistical properties of different fading channels, making it less reliant on achieving perfect, instantaneous channel state information (CSI).

• H.    Ablation Study

  We conducted an ablation study to analyze component contributions by removing: 1) the meta-discriminator, 2) the learned threshold quantizer, and 3) the bidirectional LSTMs. Table 4 presents the ablation study results for BER over a data size of 2500 symbols. The ablation study results demonstrate the superiority of the entire system, particularly in maintaining performance across diverse channels.

Table 4. Ablation study results for BER over a data size of 2500 symbols

Configuration	Rician fading channel	Rayleigh fading channel	AWGN fading channel
Full system	0.031888	0.041111	0.040308
Without Meta Discriminator	0.047647	0.070127	0.065597
Without Learned Threshold Quantizer	0.040315	0.058036	0.056902
Without BiLSTM	0.05131	0.074965	0.071921

The Full system configuration (BiLSTM autoencoder, Learned Threshold Quantizer, and Meta Discriminator) is the benchmark for best performance in terms of achieving the lowest BER among all three types of channels (Rician, Rayleigh, and AWGN). According to our tests, the BiLSTM components are the most crucial for the system's functioning. Eliminating the BiLSTM (row "Without BiLSTM" in Table 4) possesses the highest BER (worst performance) across the three channels, such as 0.074965 for Rayleigh and 0.071921 for AWGN. Such an increase in error is vital in the encoding and decoding of the message.

The Meta Discriminator plays a vital role in error correction and is highly beneficial. The second-highest increase in BER is caused by removing this (row “Without Meta Discriminator” in Table 4). In the Rayleigh channel, the value of the Bit Error Rate jumps from 0.041111 (Full system) to 0.070127. It means it has a basic effect on increasing system accuracy. The learned threshold quantizer also helps improve system performance. Analyzing the performance of the complete system shows that removing it (row “without learned threshold quantizer” in Table 4) increases BER on all channels (not as much from others). The BER in the Rician channel rise from 0.031888 to 0.040315. Due to this, it serves a function that improves accuracy, albeit to a lesser extent than the BiLSTM and Meta Discriminator.

The results of our ablation study show that although the performance of components varies, all three components: BiLSTM, Meta Discriminator, and Learned Threshold Quantizer, are needed for achieving the optimal performance of the Full system, with the first component, BiLSTM, having a significant impact.

• I.    Run-time Computation

  Table 5 presents the runtime computation for a data size of 2500 symbols (in seconds). The proposed method consistently has the lowest run time in all three channel conditions, making it the most computationally efficient of the group (2.34s, 3.21s, and 2.18s). The methods rank from slowest to fastest: DLQ, followed by DRL-FLQ, then LDPC-AEQ, PACQ, and finally the proposed method. For all methods, the computation time is fastest in the AWGN channel and slowest in the Rayleigh channel.

7.    Discussions and Future Work 7.1.    Limitations of the Proposed Method

• 7.2.    Potential Application Scenarios

Table 5. Run time computation over a data size of 2500 symbols (in seconds)

Methods	Rician fading channel	Rayleigh channel	AWGN fading channel
DLQ [1]	8.75	9.57	7.44
DRL-FLQ [25]	5.23	6.48	4.15
LDPC-AEQ [29]	4.41	5.18	3.34
PACQ [9]	3.12	4.13	2.98
Proposed method	2.34	3.21	2.18

While the proposed framework exhibits superior performance over existing approaches, several limitations warrant discussion. First, the computational overhead of the meta-discriminator, though lightweight compared to full model retraining, could introduce complications for ultra-low-power devices. The cross-attention mechanism, while effective for channel adaptation, introduces additional processing latency that could be problematic in latency-sensitive applications. Second, the current implementation assumes quasi-static channel conditions during each adaptation period, which may not hold in rapidly time-varying environments, such as high-mobility vehicular channels. Third, the method’s performance relies on the diversity of channel conditions encountered during meta-training, potentially limiting generalization to completely novel channel types not represented in the training distribution.

The quantization process itself presents inherent limitations. Although the adaptive thresholds help mitigate quantization noise, the fundamental information loss from one-bit conversion remains irreversible. This becomes particularly evident at high SNR regimes where quantization noise dominates channel noise, creating an asymptotic performance ceiling. Furthermore, the straight-through estimator used for gradient propagation through the quantizer introduces approximation errors that may affect training stability in specific scenarios.

The demonstrated capabilities suggest several promising application domains beyond conventional wireless communications. In satellite communications, where channel conditions vary significantly due to atmospheric effects and mobility, the adaptive nature of the proposed system enables it to maintain reliable links without requiring frequent retraining. The method’s data efficiency makes it particularly suitable for IoT networks with limited labeled data availability, where devices must operate in diverse and unpredictable radio environments.

Industrial wireless sensor networks represent another compelling use case. These systems often face challenging multipath environments with time-varying interference patterns, where the meta-learning approach could provide robust performance without manual reconfiguration. The framework’s ability to handle both Rician and Rayleigh fading suggests potential in hybrid terrestrial-satellite networks that experience different channel characteristics across segments.

Emerging applications in underwater acoustic communications could also benefit from this work. The extreme channel variability in underwater environments, combined with severe bandwidth constraints, aligns well with the proposed method’s strengths. Future directions should also explore scaling the method for massive MIMO systems. Concrete pathways for this include hardware-level implementations for latency-critical processing and federated metalearning models. Future extensions could explore integration with federated learning frameworks [21] for distributed adaptation across multiple nodes while preserving privacy. Future work should explore techniques like differential privacy for meta-learning updates [30] or federated learning approaches that limit centralized data collection.

8.    Conclusions

The proposed meta-learning-enhanced LSTM autoencoder with channel-adaptive quantization presents a significant advancement in robust one-bit error correction coding. By integrating bidirectional LSTM layers, learnable quantization thresholds, and a meta-discriminator with cross-attention, the system achieves superior adaptability across Rician, Rayleigh, and AWGN channels without requiring explicit retraining. Consistent improvements in BER and MSE performance are observed in the experimental results, particularly in dynamic environments. Generalization from limited training data and rapid adjustment to unseen channel conditions address critical challenges in modern communication systems.

The proposed approach succeeds through meta-learning principles, which are based on dual optimization of quantization efficiency and error correction. The meta-discriminator’s attention mechanism enables the precise characterization of channel impairments, whereas, unlike static quantization schemes, the adaptive threshold mechanism dynamically responds to channel variations. Reliable performance occurs when channel statistics deviate significantly from the training conditions. Practical viability for real-world deployment is also possible due to the system’s enhanced computational efficiency during inference. The interplay between quantization and spatial diversity presents new challenges, even when future research directions could explore extensions to higher-order modulation schemes and

MIMO systems.

Federated learning techniques may enable collaborative adaptation across distributed networks while preserving privacy. The proposed method offers a viable path toward intelligent, self-adapting communication systems operating in complex real-world environments, provided that we bridge the gap between deep learning-based error correction and practical deployment constraints. The Rician channel exhibits the lowest values of BER and MSE of 0.032 and 0.031, respectively, when considering a data size of 2500 symbols.

Acknowledgement

I confirm that the presented research work is the author's individual work. I also attest to the validity and legitimacy of the data and its interpretation. There are no conflicts of interest present, either with any individual or the organization.