Металинза для детектирования оптических вихрей с дробным топологическим зарядом

Световые пучки с оптическим вихрем широко используются в различных сферах. Впервые пучки с орбитальным угловым моментом были рассмотрены Алленом в 1992 [1], и с тех пор они используются в таких областях, как оптические линии связи [2–4], нелинейная оптика [5], квантовая обработка информации [6, 7], сверхразрешение в изображающих системах [8], оптическая манипуляция микрообъектами [9– 12]. Оптические вихри можно формировать различными способами, такими как спиральные фазовые пластинки [13], q-пластинки [14], компьютерно-синтезированные голограммы [15, 16], оптические модуляторы света [17].

Самым многофункциональным и гибким способом создания оптических вихрей являются металинзы [18]. С помощью металинз можно как формировать пучки с различными топологическими зарядами (ТЗ), так и детектировать их. Например, в [19] авторы рассмотрели создание с помощью металинзы оптических вихрей порядков 3 и 5 и оптическую манипуляцию металлическими наночастицами с помощью этих вихрей. В [20] предложена металинза, которая с помощью метода обходной фазы и пространственного разделения может создавать вихри с разными топологическими зарядами, находящиеся в разных фокусных плоскостях. В [21] рассмотрены металинзы, по- верхность которых состоит из плоских кремниевых столбиков, которые имеют определенный угол поворота вокруг своей оси в каждой отдельной точке поверхности. С помощью таких металинз можно преобразовывать падающую круговую или линейную поляризацию в отдельные световые пучки с произвольными топологическими зарядами. Авторы рассматривали целочисленные топологические заряды: –3, –2, 2, 3. Аналогичным образом создана металинза в [22], что позволяет проектировать металинзы с разными топологическими зарядами, фокусным расстояниями и расположением фокусных пятен в пространстве. В работе исследовались пучки с топологическим зарядом до 4. А в [23] авторы предложили способ детектирования топологического заряда в падающем пучке за счет комбинированной металинзы. В работе показана возможность детектирования оптических вихрей с топологическими зарядами –1 и –2. Детектированию топологических зарядов также посвящены работы [24–26]. Из упомянутых работ видно, что с помощью металинз обычно формируют целочисленные топологические заряды. Детектирование топологических зарядов также осуществляют при условии, что топологический заряд пучка является целочисленной величиной. Дробный топологический заряд в пучках при распространении быстро превращается в целочисленный, как было показано в [27]. Однако при этом в фокусной плоскости изменяется распределе- ние интенсивности, в месте расположения скачка фазы интенсивность падает до минимальных значений. В данной работе показано, как с помощью металинзы можно детектировать изначально дробный топологический заряд в падающем пучке. Моделирование в работе показало возможность определения дробного топологического заряда в диапазоне от –0,6 до –1,5. Кроме того, показано, что с помощью рассмотренной металинзы можно определять и поворот всего пучка, так как дробный топологический заряд лишает его радиальной симметрии.

Расчёт металинзы

На рис. 1 показан рельеф металинзы. Металинза рассчитана для рельефа в аморфном кремнии (показатель преломления n 1 = 4,352 + 0,486 i ), размер 8×8 мкм, 364 × 364 отсчётов, ширина канавки и ступенек одинаковые и равны 0,11 мкм, высота рельефа – 140 нм. Металинза выполнена на подложке из стекла (показатель преломления n 2 = 1,5) достаточно большой толщины, превышающей область расчетов.

а)

б)

Рис. 1. Рельеф металинзы (а), используемая для построения металинзы спираль (б) порядка – 1,5

Металинза построена из участков субволновых дифракционных решеток, чередующихся в направлении по радиусу и к центру (это создает цилиндрический векторный пучок второго порядка из падающей линейной поляризации), для фокусировки света используется спиральная зонная пластинка с ТЗ n =– 1,5 и фокусным расстоянием f = λ = 0,633 мкм. С учетом того, что падающий пучок будет иметь круговую поляризацию, это позволит фокусировать в круглое фо- кусное пятно падающее поле с ТЗ n=–0,5. Из рис. 1 видно, что разрыв фазы из-за дробного ТЗ у ЗП находится на линии Y =0, X >0, что означает, что у падающего пучка для фокусировки в круглое фокусное пятно разрыв дробной фазы должен находиться в том же месте. Ниже представлено моделирование с помощью FDTD метода с параметрами: длина волны падающего света λ = 0,633 мкм, область моделирования 10 × 10 × 2 мкм, разбиение λ /30 по всем трем координатам. Источник излучения находился в подложке, то есть толщина подложки не учитывалась в расчетах. Расстояние между источником излучения и плоскостью подложки, на которую нанесен микрорельеф, равно D =0,1 мкм.

На рис. 2 показан падающий плоский пучок и полученная с помощью FDTD метода интенсивность света в фокусе металинзы. Падающий пучок имеет левую круговую поляризацию и описывается формулой:

E ( 0 , ф ) = A ( 0 ) exp ( in ф ) , (1) i- i ;

где n =–0,5 – ТЗ, амплитуда равна A (θ) = 1 в области, ограниченной апертурой радиусом 4 мкм.

Металинза представляет собой матрицу

Я ( ф ) =

cos ф - sin ф

- sin ф

- cos ф

преобразования вектора поляризации на угол φ, умноженной на пропускание спиральной пластинки e^{in φ} с порядком n =–1,5 и функцию пропускания сферической линзы exp (– ikr ² /(2 f )). Тогда при освещении её светом с левой круговой поляризацией и вихрем с ТЗ n =–0,5 на выходе получим сходящееся в световое пятно вихревое поле с правой круговой поляризацией и топологическим зарядом n =–1 [22]:

[                                kr2 I exp 1-1,5iф-0,5iф-i2f lx f cos ф x| .

I- sin ф

- sin ф!Г 1 'I      f       kr ² VO

1I = exp| -iф-i || I.- cos фД- iJ     I      2 f lli J

Из рис. 2 видно, что при фокусировке поля с расчётным дробным ТЗ получается почти круглое фокусное пятно, причем основной вклад в него происходит за счет E z компоненты поля. Его ширина по полуспаду интенсивности вдоль осей X и Y равна FWHM x =0,404λ, FWHM y =0,438λ.

Компоненты электрического поля согласно [28] для правой круговой поляризации могут быть записаны в виде:

E x = i n ^{- 1} e n ^ф ( 1 0, „ + e ^{2 ; ф} 1 2, _n + 2 ) , E y = iⁿe^{m ф} ( I o,_n - e^21ф1 2n + 2 ) , E z = - V2 iⁿe ^{( n + 1) ф} 1 1, _{n + 1}.

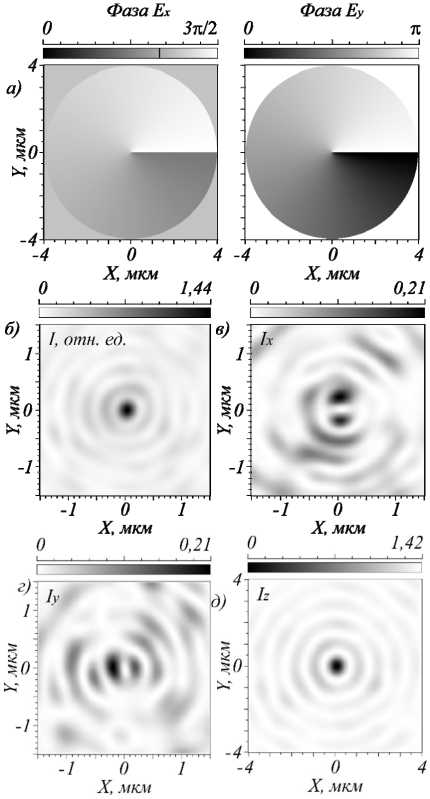
Рис. 2. (а) Фаза падающего поля, имеющего правую круговую поляризацию и фазовый вихрь с ТЗ, равным φ = – 0,5;

(б) распределение интенсивности в фокусе металинзы (негатив) на фокусном расстоянии f = 633 нм от верхнего края рельефа и интенсивность отдельных компонент |E x |² (в), |E y |² (г),|E z |² (д)

вается», с расстоянием он становится плавный, и итоговый ТЗ перестает быть дробным. При этом дробная часть ТЗ или отбрасывается, или к ней прибавляется недостающая часть до большего целого ТЗ. В данном случае ТЗ падающего поля во время распространения до металинзы составляет от 0 до 1 в зависимости от радиуса от оптической оси, на котором осуществляется его оценка, то есть он представляет собой целое число. Однако при этом в поле сохраняется неравномерность интенсивности и фазы по кругу. На рис. 3 показана интенсивность | E |² и фаза компоненты E x в подложке до металинзы: на расстоянии Z =0,1 мкм от начального поля, на расстоянии Z = 1 мкм и Z =2 мкм.

В уравнениях (3) I v,j выражается через следующий интеграл, где J j ( £ ) - функция Бесселя р-го порядка:

I v , j = ^ f jsin ^v+ 1

^ 0

01      - cos

, 3-v

X, мкм              X, мкм

Рис. 3. Интенсивность | E |² (левый столбец) и фаза E x (правый столбец) на расстоянии Z = 0,1 мкм (а), 1 мкм (б) и 2 мкм (в)

X cos1/2 (0) A (0) eikcos0 Jц (£) d 0,

аргумент функции Бесселя ^ = kr sin ( 0 ), максимальный угол интегрирования θ 0 определяется числовой апертурой апланатической системы: NA = sin ( 0 0 ). Из (4) следует: для того, чтобы на оптической оси был максимум интенсивности, основной вклад в фокусное пятно должна вносить функция Бесселя нулевого порядка, что в компоненте E z возможно при ТЗ вихря n =–1. Рис. 2 это подтверждает.

Моделирование

Известно, что дробный ТЗ не может долго существовать в пространстве [28]. Скачок фазы «сглажи-

Скачок фазы при Z =2 мкм в теневой области Y =0, X >0 составляет от 0,98 п до 1,05 п . На рис. 4 показана интенсивность в относительных единицах в центре фокусного пятна при разных расстояниях между источником излучения и металинзой: для D =0,3 мкм и D = 1,9 мкм. В плоскости источника начального поля фаза имеет скачок из-за наличия дробной части в ТЗ, но с удалением от источника на металинзу приходит свет со все более неравномерным распределением интенсивности.

Из рис. 4 видно, что, несмотря на искажение интенсивности падающего пучка, фокусное пятно почти не изменяется – максимальная разность между значениями интенсивности по полю не превышает 0,15 отн.ед.

Выше было написано, что расположение скачка фазы дробного ТЗ должно совпадать с аналогичным расположением на фокусирующей спирали в металинзе. На рис. 4 скачок находился в области Y =0, X >0. На рис. 5 показана зависимость интенсивности в фокусной плоскости на оптической оси от поворота начального поля. При этом расстояние между источником и рельефом металинзы равно D =0,1 мкм.

а)

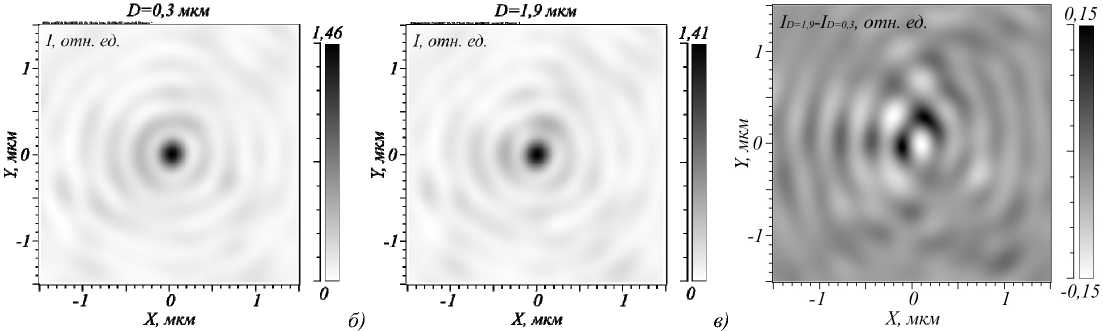
Рис. 4. Интенсивность в фокусной плоскости (негатив) при расстоянии между источником и металинзой D = 0,3 мкм (а),

D = 1,9 мкм (б), и разность между этими интенсивностями в тех же относительных величинах (в)

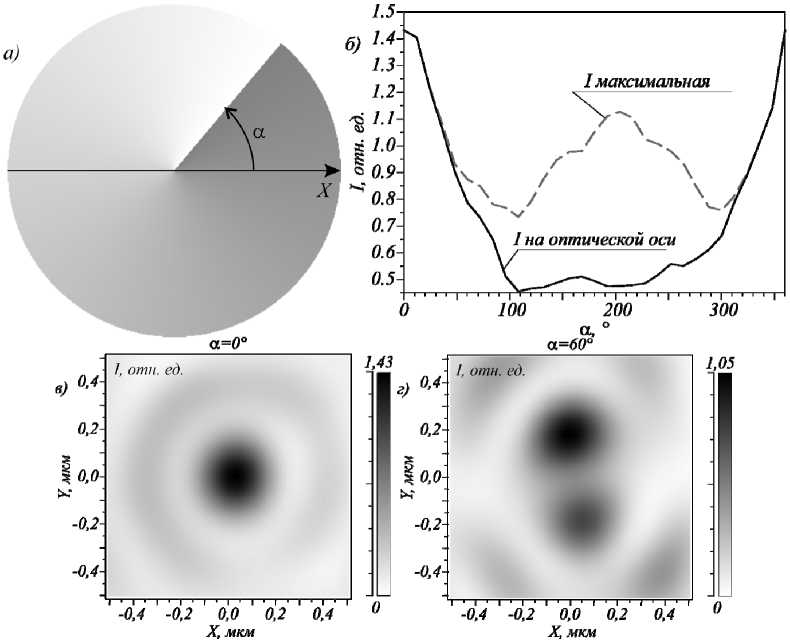
Рис. 5. Схема поворота (а), зависимость интенсивности (негатив) в центре фокусной плоскости (в одной точке на оптической оси, непрерывная линия) и глобального максимума интенсивности в фокусной плоскости независимо от его координаты (прерывистая линия) от угла поворота α начального поля с ТЗ n = – 0,5 (б), интенсивность света в фокусной плоскости при угле поворота падающего пучка α = 0° (в) и α = 60° (г)

При изменении угла α скачки фазы в падающем пучке и металинзе перестают совпадать, из-за чего изменяется фокусировка света. Это приводит к тому, что с увеличением α максимум интенсивности вначале становится меньше, а затем сдвигается относительно оптической оси. Это приводит к падению интенсивности света в центре фокальной плоскости. При этом после α > 110° максимум снова начинает расти, однако это происходит уже не на оптической оси. То есть, наблюдая за интенсивностью на оптиче- ской оси, можно оценить поворот падающего пучка с дробным ТЗ.

На рис. 6 показана зависимость интенсивности в фокальной плоскости на оптической оси от дробного топологического заряда падающего излучения ( D =0,1 мкм).

Из рис. 6 видно, что интенсивность сфокусированного света падает при изменении ТЗ пучка от расчетного. Если принять ТЗ n =–1, интенсивность на оптической оси падает в 1,58 раза, а при изменении

ТЗ на единицу (n =– 1,5) – в 6,9 раз. При этом видно, что максимальная интенсивность на оптической оси достигается при n падающего пучка, равном –0,6, а не –0,5, что говорит о некотором смещении центра фокусного пятна с оптической оси из-за асимметрии металинзы. А максимальная интенсивность в фокусе независимо от координат достигается при n =–0,7. При увеличении ТЗ фокусное пятно смещается не- много вверх на изображении, в сторону с координатами Y >0, затем его интенсивность уменьшается, а фокусное пятно распадается на отдельные максимумы меньшей величины. Если же подать на металинзу пучок с различными топологическими зарядами, но повернутый и не совпадающий по углу α с металинзой, то интенсивность на оптической оси также не достигнет максимума (рис. 7).

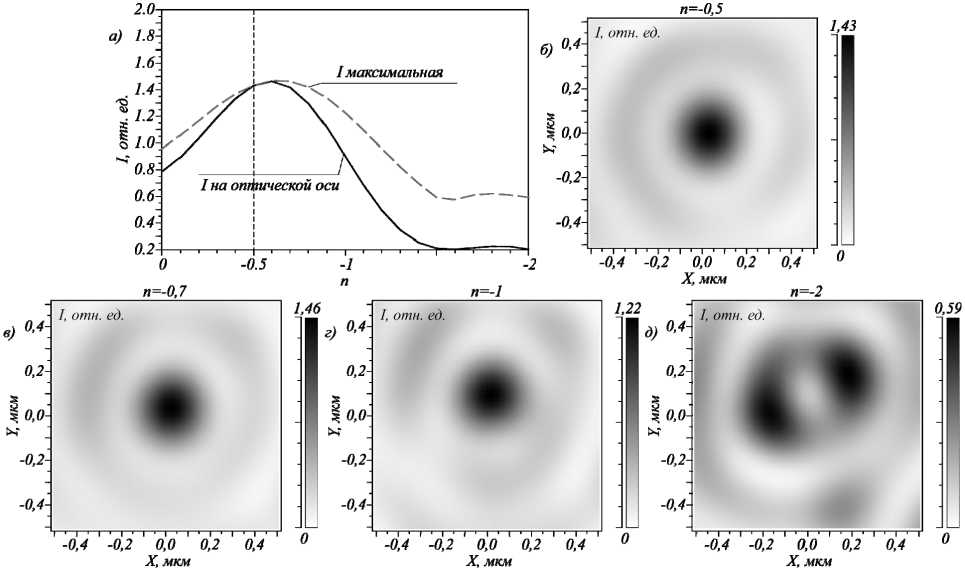
Рис. 6. Зависимость интенсивности (негатив) в фокусной плоскости (в центре и максимальная интенсивность независимо от координат) от ТЗ падающего пучка. Шаг изменения ТЗ при моделировании был 0,1

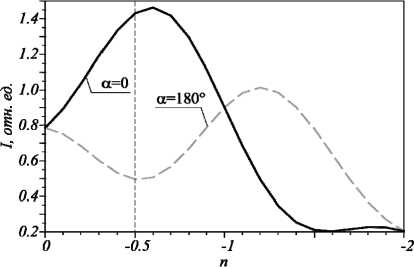
Рис. 7. Зависимость интенсивности на оптической оси при ТЗ от 0 до – 2 и углах α = 0° и 180°

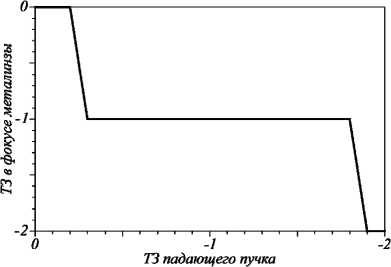
Рис. 8. Зависимость ТЗ пучка после металинзы от ТЗ падающего поля

То есть видно, что с помощью данной металинзы можно оценивать дробный топологический заряд падающего пучка в диапазоне –0,6< n <– 1,5, погрешность такого метода определения ТЗ составляет 0,1. При этом угол поворота фазовой ступеньки в падающем поле должен быть равен таковому углу у металинзы, поскольку поворот падающего пучка влияет на определение ТЗ.

На рис. 8 представлена зависимость ТЗ пучка на выходе от ТЗ пучка на входе в металинзу. ТЗ измерялся на расстоянии 0,5 мкм от центра пучка.

Видно, что ТЗ падающего поля влияет на ТЗ выходного пучка, однако в большей части диапазона от 0 до – 2 он равен –1: при начальных значениях от 0,3 до 1,8. При этом поворот падающего поля не влияет на ТЗ. Моделирование показало, что при падающем поле с ТЗ n =–0,5 независимо от поворота угла α (параметры моделирования, как для графика на рис. 5 б ) на выходе топологический заряд был равен –1. Это согласуется с (3) и рис. 2 б-д , откуда видно, что в формировании фокусного пятна основной вклад дает E z компонента поля. При n =–1 в ней участвует функция Бесселя 0-го порядка.

Заключение

В работе проведено моделирование фокусировки света с помощью металинзы, в основе которой для фокусирования света использовалась спираль с порядком –1,5. Такая металинза на выходе формирует поле с дробным топологическим зарядом, который при распространении в пространстве становится целым и равным 0 или –1. С помощью такой металинзы можно детектировать дробный топологический заряд в падающем пучке. Поле с дробным ТЗ не является стабильной пространственной модой, на месте скачка фазы образуется провал интенсивности, что видно на рис. 2. Однако это не мешает работе металинзы. В работе показано, что с помощью рассматриваемой металинзы можно детектировать дробный ТЗ в падающем поле в диапазоне –0,6< n < –1,5. При этом в центре фокусной плоскости на оптической оси в зависимости от ТЗ падающего пучка изменяется интенсивность. Моделирование показало, что изменение ТЗ падающего поля с шагом 0,1 приводит к изменению интенсивности на оптической оси в 6,9 раза – от 1,46 до 0,21 в относительных единицах (рис. 6 а ). При этом расположение в пространстве скачка фазы (темной полосы на изображениях интенсивности на рис. 3) должно совпадать со скачком фазы, записанным в структуре металинзы, что проиллюстрировано на рис. 1. При повороте падающего пучка с изначально дробным топологическим зарядом, несмотря на то, что при распространении в пространстве до плоскости металинзы он становится целым, по интенсивности в фокусной плоскости на оптической оси можно оценивать этот поворот (рис. 6 а ). Такое поведение нехарактерно для металинз, рассчитанных для детектирования пучков с целочисленным ТЗ [23]. При повороте пучка с дробным ТЗ максимум интенсивности смещается с оптической оси, что приводит к её изменению, если регистрировать интенсивность в одной точке на оптической оси. Моделирование показало, что поворот пучка от 0 до 110° приводит к падению интенсивности на оптической оси в 3,1 раза – от 1,43 до 0,46 в относительных единицах (рис. 5 б ), что позволяет измерять поворот пучка α с точностью до 10° – при таком повороте пучка интенсивность на оптической оси изменяется приблизительно на 28 %.

Работа выполнена при поддержке Российского научного фонда (грант 23-12-00236) в частях «Расчет металинзы», «Моделирование», а также в рамках выполнения работ по Государственному заданию НИЦ «Курчатовский институт» в частях «Введение», «Заключение».