Металло-диэлектрическая линза Микаэляна

Материалы с периодическим распределением показателя преломления, известные как фотонные кристаллы (ФК), становятся незаменимыми оптическими компонентами в устройствах нанофотоники [1-2]. Оптические устройства на основе ФК обладают необычными свойствами, трудно реализуемыми другими методами. Так, для ввода света в оптоволоконные структуры применяются сужающиеся ФК [3], сужаю щиеся фотонно-кристаллические световоды (ФКС) [4]. Также фокусировка может быть осуществлена с помощью фотонно-кристаллической линзы (ФКЛ), имеющей меньшие размеры и структурную совместимость с ФКС [5-8].

Пространственное изменение характеристик ячеек ФК позволяет реализовать среды с градиентно меняющимся показателем преломления. Если оптическая структура имеет период, намного меньший длины волны падающего света, то она может быть описана как среда с эффективными параметрами. Несмотря на то, что отношением периода известных реализаций ФК к длине волны нельзя пренебречь, теория эффективных сред может быть применена при условии отсутствия ненулевых дифракционных порядков при распространении волны. Градиентные среды, включающие диэлектрические стержни с меняющимся радиусом, были применены для реализации линзы Луне-берга [9]. Было показано, что использование теории эффективных сред Максвелла-Гарнетта для описания структуры даёт хорошие результаты. ФК, состоящие из отверстий с меняющимся радиусом в диэлектрической матрице, были исследованы для фокусировки и волноводного распространения света [10], для сопряжения обычного и ФК-волноводов [11], для сопряжения двух обычных волноводов [8], для фокусировки света с разными поляризациями в различные пространственные положения [12].

Диэлектрические ФК применяются для создания градиентных сред с низкими потерями, работающи х в широком волновом диапазоне. Однако разность показателей преломления для обыкновенного и необыкновенного лучей в ФК, являющаяся мерой анизотропии, невелика для диэлектрических материалов. С др угой стороны, эффективный показатель преломления градиентной среды может быть изменён в пределах показателей преломления диэлектрических материалов, из которых состоит ФК. Для создания эффективных анизотропных оптических устройств на основе ФК, позволяющих управлять светом в зависимости от поляризации, требуется применение материалов с максимальным отличием показателей преломления. Градиентные среды с металлическими включениями были исследованы в работах по моделированию устройств вращения поляризации СВЧ поля [13], поворотных сегментов волноводов [14], структ урированных металлических поверхностей для фок усировки и направленного распространения поверхностных волн [15-17].

Фотонно-кристаллическая линза

Любую линзу можно приблизительно заменить ФК-линзой, даже ту, которую трудно или невозможно сделать на текущем уро вне технологического развития. Рассмотрим, как можно рассчитать аналог линзы Микаэляна (ЛМ) [19]. Градиентная ЛМ собирает все лучи, падающие параллельно оптической оси, в точку на оптической оси на противоположной поверхности линзы. Показатель преломления ЛМ меняется от центра к краю линзы по закону:

n ( y ) = n 0 ch ¹

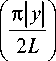
где L – фокусное расстояние, n 0 – показатель преломления на оптической оси.

Рассмотрим 2D структуру, представленную на рис. 1. Она состоит из квадратной матрицы круглых цилиндров с относительной диэлектрической проницаемостью ε 2 , расположенных в материале с относительной диэлектрической проницаемостью ε 1 .

b

ООООООООО ОоооооооО

Х1 ООООООООО -------5------

Рис. 1. Фотонно-кристаллическая линза, содержащая воздушные отверстия с меняющимся радиусом

Обозначим период кристалла d , f – относительная объёмная концентрация стержней. Рассмотрим распространение линейно поляризованной волны с длиной волны λ в вакууме и волновым вектором k . Если длина волны λ много больше периода d , то к задаче может быть применена теория эффективных сред. Эффективная диэлектрическая проницаемость ε для случая ТЕ-поляризации (вектор электрического поля параллелен оси z ) может быть представлена в виде степенного ряда с аргументом α = d / λ [10, 21, 22]:

е = е + п/3[f (1 - f )(е2 -£х)а2 + O(а4), (2)

где ε 0 – средняя относительная диэлектрическая проницаемость, ε 0 = ε 2 f + ε 1 (1 – f ).

Для случая ТМ-поляризации (вектор магнитного поля параллелен оси z )

е = -+— f ( 1 - f .         -О- а ² + O ( а ⁴ ) , (3)

a 0    3 L            е2 е1 J a О где a0 – сре днее арифм етич еско е обратн ых относительных диэлектрических проницаемостей, a0 = f /ε2 + (1 – f)/ε1.

Относительная объёмная концентрация круглых цилиндров f может быть выражена следующим образом: f = n r ² / d ² , тогда из выражения (2) для ТЕ-поляризации или (3) для ТМ-поляризации можно найти радиусы цилиндров, соответствующие выражению (1). При этом на радиус цилиндров налагаются следующие ограничения. Радиус должен быть меньше, чем d /2. Период d должен быть меньше длины волны λ. Максимальное значение радиуса должно достигаться в точках | у | = b / 2, где b - апертура линзы. Объёмная концентрация в этом случае будет составлять f max = п /4 • Из формул (2) и (3) можно получить выражения для ограничений снизу для эффективной диэлектрической проницаемости и соответственно для эффективных показателей преломления n _min = E ^in для случаев ТМ-и ТЕ-поляризаций.

Для численных экспериментов с ЛМ в воздухе были выбраны следующие параметры из работы [7]. Длина волны λ = 1,5 мкм, длина линзы равна фокусному расстоянию L = 3 мкм. Коэффициент преломления материала линзы n 0 = 1,5, ε 1 = n ₀ ² , ε 2 = 1. Апертура линзы b = 4 мкм. При данной апертуре значение n ( b / 2 ) = 0,94 является физически некорректным для приведённой структуры. В работе [22] накладывается ограничение на апертуру вида

У max ^ ^{2 L П}-1 Arch [ n 0 / n min ] •                         ⁽⁴⁾

Для данной структуры максимальная относительная объёмная концентрация воздушных стержней в материале f = п / 4 , тогда из (2) в случае ТЕ-поляризации минимальное значение эффективного показателя преломления n min = 1,13. Из (4) следует, что максимальный размер апертуры ЛМ для данных параметров b max = 3 мкм.

На рис. 2 представлена зависимость радиуса отверстий в материале ФКЛ Микаэляна (ФКЛМ) для ТЕ-поляризации, рассчитанная согласно (2), от расстояния по поперечной координате y для периода 0,125 мкм для соответствующей ФКЛ М.

Представленная зависимость, рассчитанная на основе теории эффективных сред [21], качественно отличается от зависимости, полученной в [7], где для определения оптического хода лучей через ячейку d×d , включаю щую круглое отверстие с радиусом r , рассматривалась ячейка с прямоугольным отверстием размерами 2r×d .

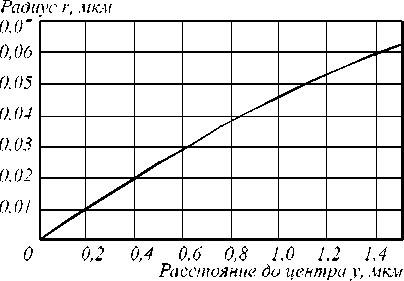
Рис. 2. Зависимость радиуса отверстий ФКЛ от расстояния от оптической оси

Результаты моделирования

Моделирование ЛМ проводилось с помощью объединённого метода конечных элементов и разложения Рэлея [23] с дискретизацией λ/100. На рис. 3 а , б представлены инвертированные распределения интенсивности поля дифракции ТЕ- и ТМ-поляризован-ных волн на ЛМ размерами 3×3 мкм с распределением показателя преломления согласно (1).

а)

О

X. MJCM

-1 0 1 у,мкм

О 1 у,мкм

б)

Рис. 3. Распределение интенсивности поля дифракции на ЛМ ТЕ- (а) и ТМ-поляризованной (б) волн

Фокусировка ТЕ-поляризованного света на поверхности ЛМ происходит с максимальной интенсивностью, достигающей 5,8. В ТМ-случае наблюдается мало выраженная фокусировка внутри элемента с меньшей интенсивностью, около 4,4. Далее моделируется прохождение света через ФКЛМ с распределением отверстий согласно рис. 2. На рис. 4 а , б представлены инвертированные распределения интенсивности поля дифракции ТЕ- и ТМ-поляризован-ных волн на ФКЛМ размерами 3×3 мкм, соответствующей рассмотренной выше ЛМ.

По сравнению с ЛМ интенсивность в фокусе ФКЛМ снизилась до 5,1 в ТЕ-случае и 3,5 в ТМ-случае. Размер пятна фокусировки для ЛМ составляет около 1,2 мкм, что согласуется с [7], для ФКЛМ около 1,35 мкм. Интенсивность в фокальном пятне ТМ-волны ФКЛМ на 31 % ниже интенсивности ТЕ-волны.

Рис. 4. Распределение интенсивности поля дифракции

на ФКЛМ ТЕ- (а) и ТМ-поляризованной (б) волн

Рассмотрим ЛМ в отсутствие ограничения (4) на апертуру линзы и минимальное значение показателя преломления n min . На рис. 5 приведено распределение показателя преломления n(у ) в ЛМ в зависимости от поперечного расстояния от оптической оси, рассчитанной в соответствии с (1), при длине линзы L = 3 мкм. Из графика видно, что при апертуре b более 3,66 мкм показатель преломления должен быть меньше 1. Было проведено моделирование ЛМ с различными апертурами и распределением показателя преломления вида (1).

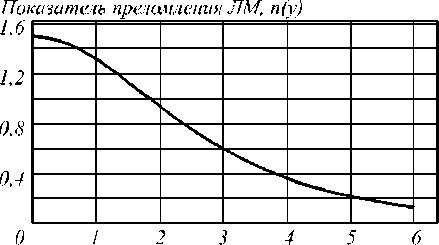
Расстояние от оптической оси, мкм

Рис. 5. Распределение показателя преломления ЛМ

На рис. 6 а представлено для иллюстрации распределение интенсивности (инвертированное) и на рис. 6 б - распределение фазы поля дифракции на ЛМ толщиной 3 мкм с апертурой b = 10,5 мкм, белый цвет соответствует сдвигу фазы 0 ° , чёрный цвет соответствует сдвигу фазы 2п. По распределению фазы можно отметить, что области ЛМ, удалённые более чем на 4 мкм от оптической оси, не дают значительного вклада в фокусировку. На рис. 7 представлена полученная зависимость максимальной интенсивности на поверхности ЛМ в фокальном пятне от размера апертуры ЛМ. С увеличением апертуры до 11 мкм максимум интенсивности возрастает и асимптотически приближается к значению 29. С дальнейшим увеличением апертуры положение фокуса и размер пятна не изменяются.

Из (2) следует, что в случае ТЕ-поляризации при заданной диэлектрической проницаемости 81 > 1 для достижения эффективной диэлектриче-ской проницаемостью 8 композитной среды зна-чений, меньших 1, диэлектрическая проницае-мость 82 должна быть меньше 1. Достичь этого возможно, заменив воздух в отверстиях соответ - ствующим материалом, например, металлом с от -рицательной реальной частью диэлектрической проницаемости. Исследуем возможность увеличе-ния интенсивности в фокальном пятне ЛМ на ос -нове композитных металло-диэлектрических сред за счёт увеличения апертуры.

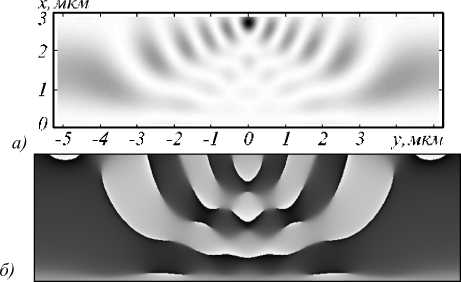
Рис. 6. Дифракция на ЛМ с апертурой 10,5 мкм: распределение интенсивности (а), распределение фазы (б)

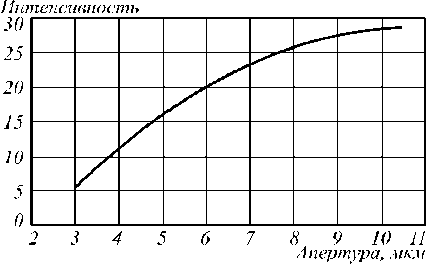
Рис. 7. Зависимость значения интенсивности в фокусе на поверхности ЛМ от апертуры

В работе [24] исследовалось распространение по- ляризованного света в периодических массивах металлических стержней в диэлектрической пластине. Было показано, что при расстоянии между серебряными стержнями менее Х/6 и при диаметре стержней не более Х/25 применение нелокальной модели однородной среды [18, 25] для моделирования диэлектрической среды, включающей массивы металлических стержней, даёт отклонение не более 1%. В работе [25] рассматри- вается матрица из диэлектрического материала с двумерной решёткой наностержней с отрицательной диэлектрической постоянной.

В [25] было показано, что для длин волн, много больших радиуса стержней, поле в компози тной периодической струк туре может быть описано с использованием диэлектрической проницаемости:

^£ TM

= £ 1 +

£ TE

2£

1 £ 1± £ 1 _ 1 f ^£2 ^-£1

И = ^£1 ⁺

£1

^£1          в ²

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^в ^^^^^^^^^*

( ^£ 2 ^-£1 ) ^{f в} Р

где г TM , г TE - диэлектрические проницаемости для ТМ- и ТЕ-поляризаций, в=^С -^ Е 1 Ц 0 — волновое число в диэлектрической структуре, to = E^ , E -энергия фотона, в p - плазменное волновое число для идеально проводящи х стержней:

( в p d ) ’ ■ '—. (7) ln lI + 0,5275

( 2 nr J

Предложенная модель также действует для диэлектриков с положительной вещественной частью диэлектрической проницаемости.

Проведём расчёт эффективного показателя преломления композитного материала, состоящего из диэлектрика ( n ₁ = 1,5) и круглых стержней из проводящего материала, например серебра ( n ₂ = 0,48 + 10,5 i , г ₂ = - 110 + 10,1 z для Z = 1,5 мкм) для ТЕ-поляризации в соответствии с (6). На рис. 8 а представлена полученная зависимость показателя преломления n + ik композитного материала от объёмной концентрации металлических стержней f .

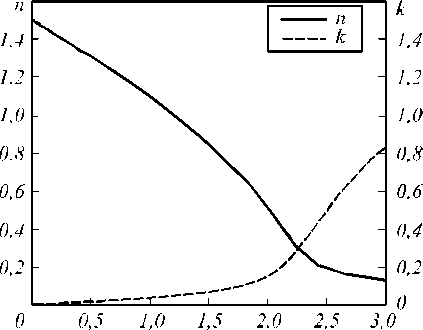
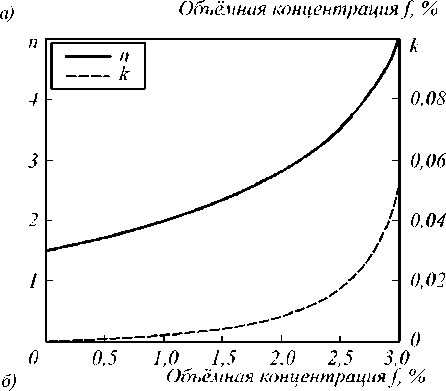
Рис. 8. Зависимость показателя преломления композитного материала от объёмной концентрации стержней f для: а) ТЕ-волны, б) ТМ-волны

На основе полученной зависимости была сконструирована металло-диэлектрическая композитная среда, дополняющая диэлектрическую ФКЛМ с апертурой 3 мкм так, чтобы общая апертура модифицированной ФКЛМ, структура которой представлена на рис. 9, составила 10,5 мкм. Объёмная концентрация серебряных стержней радиусом 7,5 нм градиентно меняется в зависимости от расстояния от оптической оси от 1 % на расстоянии 1,5 мкм до 2,8 % на расстоянии 5,25 мкм в соответствии с зависимостью (6) для получения зависимости действительной части показателя преломления композитной среды вида (1).

Рис. 9. Структура модифицированной ФКЛМ с апертурой 10,5 мкм

На рис. 10 и 11 представлены распределения интенсивности и фазы поля дифракции ТЕ- и ТМ-волн на модифицированной ФКЛМ.

а)

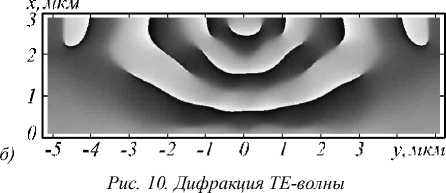
на модифицированной ФКЛМ:

а) распределение интенсивности, б) распределение фазы

Рис. 11. Дифракция ТМ-волны на модифицированной ФКЛМ: распределение интенсивности (а), распределение фазы (б)

Можно отметить, что в ТЕ-случае крайние области элемента обладают слишком большим поглощением, чтобы давать существенный вклад в фок у-сировку. Из рис. 10 б видно, что рабочая апертура данного элемента составляет около 8 мкм. В ТМ-случае вклад в осевую фок усировк у наблюдается только от диэлектрической фотонно-кристаллической линзы. Максимальная интенсивность на по- верхности составляет 11,5 в ТЕ-случае и 3,5 в ТМ-случае. Распределение интенсивности поля дифракции на поверхности представлено на рис. 14 а.

Далее сконструируем композитн ую металло-ди-электрическ ую ЛМ, использ уя зависимость пока за-теля преломления от объёмной концентрации се-ребрян ых стержней для ТЕ-поляризации на рис. 8 а и заменив центральную фот онно-кристаллическ ую диэлектрическ ую о бласть п олностью к омпозитной средой, состоящей из серебряных стержней радиусом 7,5 нм в диэлектрической сре де с диэлектрической проницаемостью ε 1 = 2,25. Аперт ура элемента также составляет 10,5 мкм. Объёмная концентрация стержней градиентно меняется в зависимости от расстояния от оптической оси от 0 % на оптической оси (расчётный показатель преломления для ТЕ-и ТМ-случаев n = 1,5) до 2,2 % на расстоянии 5,25 мкм (расчётный показат ель преломления для ТЕ-случая n = 0,27 + i 0,35, для ТМ-случая n = 1,54). Расположение стержней в диэлектрической пластине толщиной 3 мкм и распределение интенсивности и фазы поля дифракции ТЕ-и ТМ-поляризованных волн приведено на рис. 12 и 13.

Рис. 12. Дифракция ТЕ-волны на композитной ЛМ: распределение интенсивности (а), распределение фазы (б)

Рис. 13. Дифракция ТМ-волны на композитной ЛМ: распределение интенсивности (а), распределение фазы (б)

В ТЕ-случае наблюдается осевая фок усировка с максимальной интенсивностью 7,2 на поверхности. В ТМ-случае вследствие малого отклонения показателя преломления в композитной среде в соответствии с зависимостью на рис. 8 б, её влияние на прохождение волны незначительно. Распределение интенсивности поля дифракции на поверхности представлено на рис. 14 б .

11нт енатност ь

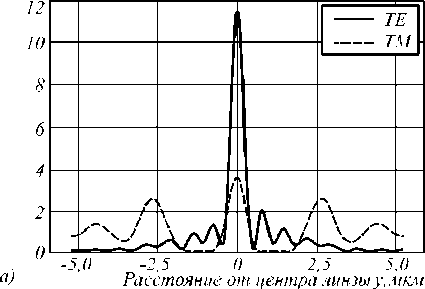
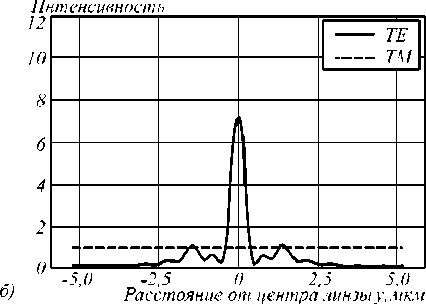
Рис. 14. Распределение интенсивности поля дифракции на поверхности модифицированной ФКЛМ (а) и композитной ЛМ (б)

Сконструируем композитную металлодиэлектрическую ЛМ, используя зависимость показателя преломления от объёмной концентрации серебряных стержней для ТМ-поляризации на рис. 8 б радиусом 7,5 нм в аналогичной диэлектрической среде с диэлектрической проницаемостью ε 1 = 2,25. Апертура элемента также составляет 3 мкм. Объёмная концентрация стержней градиентно меняется в зависимости от расстояния от оптической оси от 25 % на оптической оси (расчётный показатель преломления для ТЕ-случая n = 0,19 + i 5,1, для ТМ-случая n = 2 + i 0,002) до 0 % на расстоянии 1,5 мкм (расчётный показатель преломления для ТЕ-и ТМ-случаев n = 1,5). Расположение стержней в диэлектрической пластине толщиной 3 мкм и распределение интенсивности и фазы поля дифракции ТЕ- и ТМ-поляризованных волн приведено на рис. 15. В ТЕ-случае волн ы в элементе быстро затухают, на поверхности элемента интенсивность прошедшей волны нулевая. Отражение от элемента 94 %. В ТМ-случае максимальная интенсивность в фокальной точке на поверхности равна 8,5.

Заключение

Моделированием объединённым методом конечных элементов и разложения Релея было исследовано прохождение ТЕ- и ТМ-поляризованного света через линзы Микаэляна, сконструированные на основе фотонно-кристаллических сред и композитных металло-диэлектрических сред.

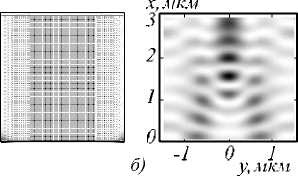
Рис. 15. Распределение интенсивности поля дифракции на композитной ЛМ ТЕ- волны (а) и ТМ- волны (б), распределение фазы в ТМ-случае (в)

Для преодоления ограничения снизу на значение показателя преломления в линзе Микаэляна и увеличения её апертуры было предложено использовать композитную металло-диэлектрическую среду, состоящую из диэлектрической среды, включающей периодические массивы металлических стержней диаметром 15 нм, технологически трудно реализуемую в настоящее время. Показано, что дополнение градиентной композитной средой фотонно-кристаллической линзы повышает интенсивность в фокальном пятне в 2 раза по сравнению с фотонно-кристаллической линзой, при этом апертура линзы увеличивается в 3,5 раза. Линза, полностью состоящая из композитной среды и рассчитанная для ТЕ-поляризации, позволяет получить увеличение интенсивности на 40 %. Рассчитанная для ТМ-поляризации линза из композитной среды позволяет получить увеличение интенсивности в фокусе в 2,4 раза по сравнению с ФКЛМ аналогичной апертуры, при этом 94 % ТЕ-поляризованного света отражается от элемента.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках реализации ФЦП «На учные и научно-педагогические кадры инновационной России» на 2009-2013 годы (гос ударственные контракты № 02.740.11.0841, № 02.740.11.0805 и № 14.740.11.0016), грантов РФФИ 10-02-90726-моб_ст и Президента РФ поддержки ведущи х научных школ (НШ-7414.2010.9).