Method of Performing Operations on the Elements of GF(2m) Using a Sparse Table

The task of protecting information today is especially important because due to the rapid development of cloud computing, the risk of breaking ciphers is growing.

Modern cryptosystems are based on the theory of finite fields [1-5]. Increasing the cryptographic strength of existing ciphers is realized by increasing the recommended key length. The consequence of increasing the length of the key is a significant increase in the number of basic operations for encryption. Thus, the problem of reducing the computational complexity of existing methods of performing operations on elements of finite fields is urgent.

One of the problems of information transfer is increasing the interference resistance of technical systems conditions of influence of both natural interferences and created artificial interferences. One way to ensure the integrity of data in the transmission of information is the use of error-correcting codes. Currently, turbo codes, BCH codes, Reed-Solomon codes and Fire codes are most often used for data encoding with error correction [6-7]. These correction codes are based on the theory of finite fields.

Also, issue of the privacy-preserving data is important in modern information systems, in particular when building data analysis systems and artificial intelligence. Among the methods of protecting such data are homomorphic encryption (in particular, the ElGamal scheme) and secure multi-party computing that uses Galois field arithmetic.

Two types of finite fields are used in both cryptographic systems and correction codes: GF ( p ) and GF ( p^m ). The finite fields GF ( p ) are more studied than GF ( p^m ). In modern data processing systems, the partial case of GF ( p^m ) is increasingly used, namely GF (2 ^m ) [8-12]. Therefore, the task of developing new methods of performing operations on the elements of GF (2 ^m ) is urgent.

The existing methods of performing operations on the elements of the Galois field are divided into two types: 1) using only the polynomial representation, such a method is characterized by high computational and time complexity; 2) the use of a tabular method, this method allows to reduce the computational and time complexity, but requires a lot of RAM to store a complete table of the correspondence of the polynomial and power representation of the elements of the Galois field.

Thus, the main goal of this study is to develop a method for performing operations on elements of finite fields GF (2 ^m ), which will allow to reduce the computational complexity of information protection systems and errorcorrecting coding, and it will also allow to increase the speed of encryption.

2.    Problem Statement

Asymmetric cryptography mostly uses finite fields with order more than 2128. Symmetric cryptographic systems and correction codes use Galois fields with an element number that generally does not exceed 220 (for example, AES and Reed-Solomon code).

Field elements of GF (2 ^m ) can be represented in a polynomial or normal basis. Existing data processing systems mostly use a polynomial basis, since it allows storing polynomials that are elements of the field, as ordinary numbers given in a binary numeral system.

There are two ways to represent the elements of GF (2 ^m ) in a polynomial basis: polynomial and power representation.

When a polynomial representation is used in GF (2 ^m ), algebraic operations are performed by the module of an irreducible polynomial. The most computationally costly operations in a polynomial representation are the calculation of the multiplicative inverse element and exponentiation. The algorithms for performing these operations in an exponential representation have less computational complexity, however, the computational complexity of the addition and calculation of the additive inverse element operations increases, and the additional RAM is required to perform them.

Thus, the task of developing a method of performing operations on the elements of GF (2 ^m ), which combines different ways of representing the elements of the field and has a high speed, is urgent.

3.    Literature Review

The tabular method of performing operations on field elements of GF (2 ^m ) [1, 2, 12-15] provides the fastest performance among the existing methods, so we will consider this method in more detail.

The elements of GF (2 ^m ) can be represented as the power of a primitive element (exponential representation) and as a polynomial of a degree less than m (polynomial representation). For example, the elements of GF (2⁴) are shows in these representations in Table 1.

Numerical representation is equivalent to polynomial representation of field elements. To obtain a numerical representation, it is necessary to write the coefficients of the polynomial as binary digits.

There are additive (addition, calculation of additive inverse element, subtraction) and multiplicative (multiplication, calculation of multiplicative inverse element, division, exponentiation) operations over a finite field [1, 3].

Tabular storage of field elements is used to achieve maximum performance. With this approach, it is advisable to perform additive operations on the polynomial representation of the field elements [1, 8], and multiplicative operations on the exponential representation of elements (Fig. 1). Since different operations require the representation of elements in different forms, there is a need for operations to convert the polynomial representation of the element of GF(2m) to exponential and vice versa.

Operations on the elements of GF (2 ^m ) can be implemented in both software and hardware.

Thus, in the hardware implementation, the unit for performing operations on the elements of GF (2 ^m ) should support the execution of a set of commands given in Table 2.

This unit is implemented in such a way that the input must always receive a polynomial representation of the field elements and the result obtained at the output of the operations unit will also be represented in a polynomial representation [7].

The ADD_SUB operation is hardware implemented as a two-input XOR element with m bit operands and provides for the obtaining of operands at the input in a polynomial representation.

Table 1. Representation of the elements of GF (2 4 ) modulo irreducible polynomial p ₄ ( x ) = x ⁴ + x + 1

Exponential representation		Polynomial representation	Numerical representation
Power of the primitive element a of the field with a non-negative exponent	Power of the primitive element a of the field with a negative exponent		Binary	Decimal
–	–	0	0000	0
α 0	α –15	1	0001	1
α 1	α –14	α	0010	2
α 2	α –13	α 2	0100	4
α 3	α –12	α 3	1000	8
α 4	α –11	a + 1	0011	3
α 5	α –10	a 2 + a	0110	6
α 6	α –9	a 3 + a 2	1100	12
α 7	α –8	a 3 + a + 1	1011	11
α 8	α –7	a 2 + 1	0101	5
α 9	α –6	a 3 + a	1010	10
α 10	α –5	a 2 + a + 1	0111	7
α 11	α –4	a 3 + a 2 + a	1110	14
α 12	α –3	a 3 + a 2 + a + 1	1111	15
α 13	α –2	a 3 + a 2 + 1	1101	13
α 14	α –1	a 3 + 1	1001	9

Address	Non-negative exponent of the primitive field element a	Numeric value of the field element
0 0 0 0	—	1(«°)		2”=16
00 0 1	0	2 (a1)
00 10	1	4 (a2)
0 0 11	4	8 (a3)
0 10 0	2	3 (a4)
0 10 1	8	6 (a5)
0 110	5	12 (a6)
0 111	10	11 (a7)
10 0 0	3	Б (a3)
10 0 1	14	10 fa9)
10 10	9	7 (»10)
10 11	7	14 (я11)
110 0	6	15 (a12)
110 1	13	13 (я13)
1110	11	9 (я14)
1111	12	1 (я15)

Fig.1. Tabular storage of GF (2 ⁴ ) elements with irreducible polynomial x ⁴ + x + 12

Table 2. Command system of the unit for performing operations on field elements of GF (2 ^m )

Mnemonics	Description of mnemonics	Purpose of the operation
ADD_SUB	ADDition and SUBtraction	Addition and subtraction of field elements
MULT	MULTiplication	Multiplication of field elements
DIV	DIVision	Division of field elements
POW	POWer	Exponentiation of field elements
INVM	INVerse Multiplicative	Calculating a multiplicative inverse field element
CDP	Convert Digit to Power	Conversion of numerical (polynomial) representation of the field element of GF (2 m ) into exponential
CPD	Convert Power to Digit	Conversion of exponential representation of a field element of GF (2 m ) into numerical (polynomial)

Mathematically, MULT and DIV operations involve operands in exponential representation, however, in hardware they are implemented in such a way that the values of operands are received in a polynomial representation, then converted to exponential representation, and involve a unit of microoperations modulo 2 ^m – 1 to add / subtract operands modulo 2 ^m – 1 over the value of the exponential representation and then the result is converted into a polynomial representation.

The POW operation involves the first operand in the exponential representation, and a second operand (power) is a number. The first operand comes to the input in the polynomial representation, turns into an exponential representation, and then involves a unit of microoperations modulo 2 ^m – 1 for multiplying operands modulo 2 ^m – 1, and the result is converted into a polynomial representation.

The INVM operation involves the operand in an exponential representation, but similarly to the previous three operations, the operand first arrives in a polynomial representation, then is converted to an exponential representation, and then the microoperation unit moduo 2 ^m – 1 is involved to invert the operand.

The CDP and CPD operations are implemented tabularly (Fig. 1), namely by storing all elements of GF (2 ^m ) in the ROM.

When performing the CDP , the address must be a numerical representation of the field element, and the appeal should be to the corresponding row on the left side of the table (the right part of the table is not used). The result of reading from the ROM will be a non-negative exponent of the primitive field element a.

When performing the CPD operation, the address must be a non-negative exponent of the primitive field element, and the appeal should be to the corresponding row on the right side of the table (the left part of the table is not used). The result of reading from the ROM will be the numerical value of the field element.

4.    Proposed Methodology and Method of Performing Operations on Field Elements of GF(2m)

The main disadvantage of the tabular method for performing operations on elements of GF (2 ^m ) is the use of a large amount of memory to store a table of correspondence between polynomial and exponential representation of field elements. This disadvantage can be remedied by storing a sparse correspondence table between the polynomial and the exponential representation of the field elements.

Address in the new table	Address in the initial table	Non-negative exponent of the primitive field element a	Numeric value of the field element
000	00 00	-	1	I"")
00 1	00 1 1	4	8	И
0 1 0	0 110	5	12	И
0 I 1	I 00 1	14	10 Ю
1 0 0	1100	6	15	(-"
1 0 1	Mil	12

Fig.2. Sparse table

For example, the table of elements of GF (2⁴) (Fig. 1) can be sparse if every third row of the table is saved (Fig. 2 , in this case the degree of sparsity к = 3, namely the amount of memory required for storage the table is reduced by 3 times.

In the considered example the function of division by 3 is used (each line which number is multiple of three is left in the table). In general, any mathematical function that has an inverse can be used to reduce the table. For example, the logarithm function on a defined basis can be used and rows in the table, the numbers of which when using the selected logarithmic function give an integer, can be left. However, this choice of the sparse function will cause uneven sparsity of the table – the farther from the beginning of the table, the sparser it will be. Therefore, it is advisable to use this approach if there is a priori information about the law of distribution of input data, and the law itself differs from the uniform; otherwise, it is advisable to use a function that provides uniform thinning of the table. This is the function of division by the number k , where k is the degree of sparsity.

After selecting the sparsity function, it is necessary to build an algorithm for converting the elements of GF (2 ^m ) from exponential representation to numerical and vice versa.

The complete table of correspondence between the polynomial and exponential representation of elements of GF (2 ^m ) has the following property: numerical representations of field elements are arranged in ascending order of the corresponding values of exponential representation (this is illustrated by the second column in Fig. 1). This property provides the ability to find the base element for an arbitrarily given element in the exponential representation in a sparse table. Using the found base element, it is possible to get a numerical representation of a given element, which requires no more than ^ k J iterations.

The address of the base element α^r in the sparse table is found by integer division of the exponent of a given element α^d , namely d , by k with rounding to the nearest whole. Denote the result of the integer division addr , the value in the second column of the table at the address addr denote s . Thus, α^r is an exponential representation of the base element, and s is a numerical representation. The next steps depend on whether rounding α^d was performed to the smallest or largest whole (algorithm 1).

If rounding was performed to the smallest integer ( r <  d ), then the numerical representation corresponding to the element α^d is found by reproducing the process of constructing a fragment of the table of correspondence of numerical and exponential representation of elements of GF (2 ^m ), starting from the base element α^r to element α^d . That is, the numerical representation of the element is found by shifting to the left the value of 5 by {Ц bits and obtaining the remainder of dividing the result of the shift by an irreducible polynomial, where the symbol { } indicates the remainder of division.

If rounding was performed to the largest integer ( r >  d ), then the numerical representation corresponding to the element α^d , is found by reproducing the process, which is inverse to the process of constructing a fragment of the table of correspondence of numerical and exponential representation of elements of GF (2 ^m ), starting from the element α^d to the base element a^r . The total number of iterations is k - {Ц. If the least significant digit is 0, then one iteration consists in shifting the operand to the right by one digit, otherwise, the addition of an irreducible polynomial and the shifting to the right by one digit are performed.

Algorithm 1. Conversion of an exponential representation to a polynomial using a sparse table

2 ^m

Input: table [ — х 21, ir [ 1 х m ], pow E N, k E N

Output:  res  [ 1 х  m ]

_L addr _ [ pow J; c _ { pow }

2 ^m

• 2.    if I c < k - c OR addr = —)

  • 2.1.    res ← table  [ addr , 2]  {  res – polynomial }

  • 2.2.    j ← 0

  • 2.3.    while (j' <  c )

    • 2.3.1.    while ( deg ( res ) <  m and j

• a)    res ^ res ■ x { x - monomial }

• b)    j ^ j + 1

• 2.3.2.    end while

• 2.3.3.    if ( deg ( res ) >  m )

• a) res ^ res + ir

• 2.3.4.    end if

• 2.4.    end while

• 3.    else

  • 3.1.    addr ← addr + 1

  • 3.2.    c ← k – c

  • 3.3.    res ^ table [ addr , 2]  { res - polynomial }

  • 3.4.    j ← 0

  • 3.5.    while (j' <  c )

    • 3.5.1.    if (res [0] == 1)

•                 a) res ← res + ir

• 3.5.2.    end if

• 3.5.3.    while ( res [0] == 0 and j

• 3.5.4.    end while

• 3.6.    end while

• 4.    end if

• 5.    return res

                a) res ← res / x   {  x – monomial }

                b) j ← j + 1

Consider examples.

For the element α ⁷ of GF (2⁴) with the irreducible polynomial x ⁴ + x + 1, using a sparse table (Fig. 2), find its polynomial representation. The degree of sparsity к = 3.

Integer division 7 by 3 with rounding to the nearest whole gives 2 (address of the base element in a sparse table), namely addr = 2. At address 2 we find the numerical representation of the base element s = 1100. Shift the value of s to { d } = { 7 } =1 digit to the left and get ⁵ = 11000. Divide this result with the remainder by the irreducible polynomial 10011 (for this example the division is reduced to a single addition of the irreducible polynomial) and get the desired value, which is equal to 1011 (the correctness can be checked using Fig. 2).

For the element α ¹⁴ of GF (2⁴) with the irreducible polynomial x ⁴ + x + 1, using a sparse table (Fig. 2), find its polynomial representation. The degree of sparsity к = 3.

Integer division 14 by 3 with rounding to the nearest whole gives 5 (address of the base element in a sparse table), namely addr = 5. At address 5 we find the numerical representation of the base element s = 0001. The total number of iterations is k - { d } =3 - { 14 } =1. The lowest digit s is equal to 1, so we add an irreducible polynomial (result 10010) and shift one digit to the right, we get 1001 (the correctness can be checked using Fig. 2).

Consider the approach to the conversion of the elements of GF (2 ^m ) from a polynomial (numerical) representation to an exponential.

In the sparse table there are rows of the whole table, the addresses of which in the whole table are multiples of k , so it is necessary to go from the specified numerical representation of element d to the numerical representation of the field element multiple of k , namely to the numerical representation for which there is a corresponding exponential representation in sparse table. Thus, a basic element with a known exponential representation is obtained. Next, from the obtained exponential representation of the base element, it is necessary to obtain an exponential representation of the desired element.

The conversion from the specified numerical representation of the element d to the numerical representation of the field element, which is a multiple of k , is carried out by reproducing the process of constructing a fragment of the table of numerical and exponential representations of elements of GF (2 ^m ), or the process inverse to it (algorithm 2 and 3).

Algorithm 2. Conversion of a polynomial representation to an exponential one with a search for the base element at the top of the sparse table

Input:  table  [ 2 ^m  х 2],  pol ,  ir  [ 1 х  m ],  k ∈ N

Output:  res ∈ N

• 1.    dec ← Bin 2 Dec ( pol )

• 2.    count ← 0

• 3.    while ({ dec } ^ 0)

  • 3.1.    if ({ dec } ^ 0)

    • 3.1.1.    pol ← pol + ir

    • 3.1.2.    pol ← pol / x

    • 3.1.3.    dec ← Bin 2 Dec ( pol )

    • 3.1.4.    count ← count + 1

  • 3.2.    end if

  • 3.3.    while ({ dec } ^ 0 and { dec } == 0)

    • 3.3.1.    pol ← pol / x

    • 3.3.2.    dec ← Bin 2 Dec ( pol )

    • 3.3.3.    count ← count + 1

  • 3.4.    end while

• 4.    end while

• 5.    dec ← dec / k

• 6.    return table [ dec , 1] + count

Algorithm 3. Conversion of a polynomial representation to an exponential one with a search for the base element at the bottom of the sparse table

Input:  table  [ 2 ^m  х 2],  pol ,  ir  [ 1 х  m ],  k ∈ N Output:  res ∈ N

• 1.    dec ← Bin 2 Dec ( pol )

• 2.    count ← 0

• 3.    while ({ dec } ^ o)

  • 3.1.    while ({ dec } ^ 0 and deg ( pol) <  m )

    • 3.1.1.    pol ← pol ⋅ x

    • 3.1.2.    dec ← Bin 2 Dec ( pol )

    • 3.1.3.    count ← count + 1

  • 3.2.    end while

  • 3.3.    if (deg ( pol) = m )

    • 3.3.1.    pol ← pol + ir

    • 3.3.2.    dec ← Bin 2 Dec ( pol )

  • 3.4.    end if

• 4.    end while

• 5.    dec ← dec / k

• 6.    return table [ dec , 1]- count

Consider this process in more detail.

The search for the base element is iterative, until the next result is a multiple of k .

If the search for the base element is performed by reproducing the process inverse to the process of constructing a fragment of the table of correspondence of numerical and exponential representation of the elements of GF (2 ^m ), namely at the top of the sparse table, then each iteration is the following steps.

• •    If the least significant digit of the element d is 1, then add an irreducible polynomial to the operand. Record the result in d .

• •    Shift d to the right by one digit until a value multiple of k is got, or until the least significant digit d becomes one.

When performing the second step of the iterative process, it is necessary to count the number of shifts performed. Let the total number of shifts to the right be equal to count .

After obtaining the address of the base element in the complete table, its address in the sparse table is obtained by dividing by k , thus ^d . Next, it is necessary to take the exponential representation from the sparse table at ^d address from the first column and add the count value to it. The result obtained will be the desired exponential representation.

If the search for the base element is performed by reproducing the process of constructing a fragment of the table of correspondence of numerical and exponential representation of the elements of GF (2 ^m ), namely at the bottom of the sparse table, then each iteration consists of the following steps.

• •    Shift d to the left by one digit until a value multiple of k is got, or until the most significant digit d (digit with number m when numbered from zero) becomes one.

• •    If the highest significant digit of the element d is 1, then add an irreducible polynomial to the operand. Record the result in d .

When performing the first step of the iterative process, it is necessary to count the number of shifts performed. Let the total number of shifts to the right be equal to count .

After obtaining the address of the base element in the complete table, its address in the sparse table is obtained by dividing by k , thus -. Next, it is necessary to take the exponential representation from the sparse table at - address from the first column and subtract count value from it. The result obtained will be the desired exponential representation.

Consider examples.

Suppose that for element 1010 2 of GF (2⁴) with the irreducible polynomial x ⁴ + x + 1, using a sparse table (Fig. 2), it is necessary to find its exponential representation. The degree of sparsity к = 3.

According to the first approach, the input operand is checked for a multiplicity of 3, because 1010 2 is not a multiple of 3, then the iterative process is run.

The first iteration. A parity check is performed. The input operand is a multiple of 2, so go to the shifts and perform one shift. The intermediate result 1012 (count = 1) is obtained.

The second iteration. Add the irreducible polynomial, get 10110 2 . Shift the result to the right, get 1011 2 ( count = 2).

The third iteration. Add the irreducible polynomial, get 11000 2 . Shift the result to the right, get 1100 2 ( count = 3).

A number multiple of 3 was got, namely 12. Divide it by 3, we get 4. At address 4 in the sparse table, we find the value of the exponential representation, equal to 6. To the resulting value add the accumulated number of shifts and get 9.

According to the second approach, the input operand is checked for a multiplicity of 3, because 1010 2 is not a multiple of 3, then the iterative process is run.

The first iteration. A check for multiplicity 3 and equality to 1 of the most significant digits (digit with number m when numbered from zero) is performed. Both conditions are not met, so go to shifts and perform one shift. The intermediate result 10100 2 ( count = 1) is obtained. Add the irreducible polynomial, get 111 2 .

The second iteration. Shift by two bits to the left, get 11100 2 ( count = 3). Add the irreducible polynomial, get 1111 2 .

A number multiple of 3 was got, namely 15. Divide it by 3, we get 5. At address 5 in the sparse table, we find the value of the exponential representation, equal to 12. From the resulting value subtract the accumulated number of shifts and get 9.

In the examples used, the value of k is equal to 3, however, for hardware implementation, it is necessary to choose the value of the degree of sparsity, which is power of 2. With this approach, each subsequent value of the degree of sparsity allows to reduce the bit size of the address by one bit, as well as greatly simplify the operation of integer division by k in algorithms for converting from numerical to exponential representation and vice versa, because in this case, the operation of integer division degenerates into a bit shift operation.

5.    Analysis of the Proposed Method

Let's estimate the number of iterations when converting the elements of the field from the exponential representation to the numerical one and vice versa.

Conversion from exponential representation to numerical representation is performed by at most ^ k J iterations (shift by one bit and addition of irreducible polynomial).

When converting from a numerical representation to an exponential one, the largest number of iterations (shift by one bit and addition of an irreducible polynomial) will be equal to the maximum value of pairwise adjacent differences of exponents.

For example, if к = 3, the following exponents will remain in the sparse table (Fig. 2): 4; 5; 14; 6; 12. Arrange in descending order, pre-adding zero: 0; 4; 5; 6; 12; 14. Calculate the pairwise differences: 4; 1; 1; 6; 2. The largest value of the pairwise differences is 6. Therefore, in the worst case, to perform the conversion from numerical to exponential representation will require 6 iterations.

To evaluate the efficiency of using a sparse table, let's compare the number of elementary operations required to perform operations on the elements of GF (2 ^m ), using a sparse table and polynomial basis.

Multiplicative inverse element calculation and exponentiation operations require one operand (unary operations), which is an element of GF (2 ^m ), and multiplication and division operations require two (binary operations). Therefore, when using a sparse table for unary operations, it is necessary to perform the conversion from a polynomial to a exponential representation of only one operand, and for binary – two. After performing each of these operations, the result must be converted from an exponential representation to a polynomial.

Over the exponential representation, the multiplicative inverse element calculation requires two m -bit operations (addition and reduction modulo 2 ^m – 1), multiplication also two m -bit operations (addition and reduction modulo 2 ^m – 1), division - three m -bit operations (inversion, addition, and reduction modulo 2 ^m - 1), exponentiation - 2.5 • t operations on the m -bit operands, where t is the number of bits in the exponent (Table 3; 4).

Table 3. Experimentally obtained an average estimate of the number of additions / shifts operations using a table with a degree of sparsity 8

Operations on finite field elements of GF (2 m )	m
	5	10	13	17	20
Multiplicative inverse element calculation	14.88	20.55	21.80	20.12	20.77
Exponentiation	12.88 +2.5* t	18.55 +2.5* t	19.80 + 2.5* t	18.12 +2.5* t	18.77 +2.5* t
Multiplication	27.91	39.00	41.62	38.14	39.42
Division	28.91	40.00	42.62	39.14	40.42

Table 4. Experimentally obtained an average estimate of the number of additions / shifts operations using a table with a degree of sparsity 16

Operations on finite field element	m
	5	10	13	17	20
Multiplicative inverse element calculation	29.48	39.54	43.02	41.30	42.81
Exponentiation	27.48 + 2.5* t	37.54 + 2.5* t	41.02 + 2.5* t	39.30 + 2.5* t	40.81 + 2.5* t
Multiplication	57.32	77.19	84.06	80.60	83.54
Division	58.32	78.19	85.06	81.60	84.54

Let's find the number of bit operations when using exclusively polynomial representation to perform operations on the elements of GF (2 ^m ).

The multiplication operation of field elements (multiplying polynomials and modulo reduction by an irreducible multiplier) requires on average m shifts and m additions over m -bit operands; operation of multiplicative inverse element calculation (using the extended Euclidean algorithm) – 2 m shifts and 2 m additions; division (calculation a multiplicative inverse element to the second operand and multiplication of the obtained result by the first operand) – 3 m shifts and 3 m additions; exponentiation (binary multiplication algorithm) – 1.5 ⋅ m ⋅ t shifts and 1.5 ⋅ m ⋅ t additions, where t is the number of bits in exponent (Table 5).

Table 5. The average estimate of the number of additions / shifts operations when using a polynomial representation

Operations on finite field elements	m
	5	10	13	17	20
Multiplicative inverse element calculation	20	40	52	68	80
Exponentiation	15* t	30* t	39* t	51* t	60* t
Multiplication	10	20	26	34	40
Division	30	60	78	102	120

6.    Experimental Research with Discussion

Experimental research was conducted on a computer, which has a Windows 8.1 operating system with the following characteristics: 2Gb of RAM, Pentium Dual-Core 2.30 Hz.

To determine the average number of addition / shift operations using a sparse table, the software was developed using the C# programming language in the Visual Studio 2015 development environment. Experimental investigations were performed on random input sets containing 1,500 operands and elements of a given field.

The average estimate of the number of bit operations when using a polynomial representation to perform operations on the elements of GF (2 ^m ) is shown in Table 5. Figs. 3-5 show diagrams that make it possible to compare the computational complexity of methods for performing operations on elements of GF (2 ^m ) in hardware implementation by the number of elementary operations Q (shift and bitwise addition operations). The value that is equal to 8 was chosen as a degree of table sparsity for the proposed method.

r> Execution of operation at tabular representation of field elements (sparse table)

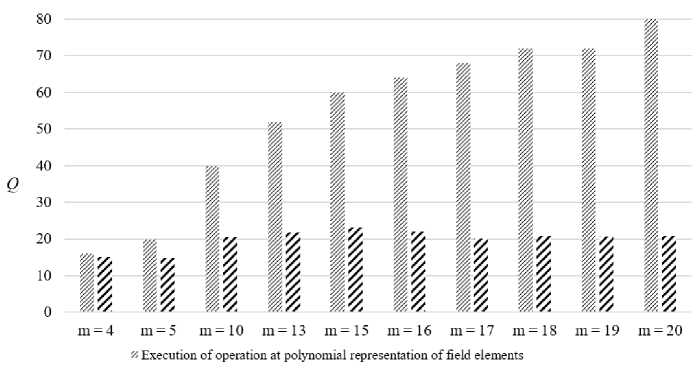
Fig.3. The number of elementary operations during the multiplicative inverse element calculation of field elements of GF (2 ^m )

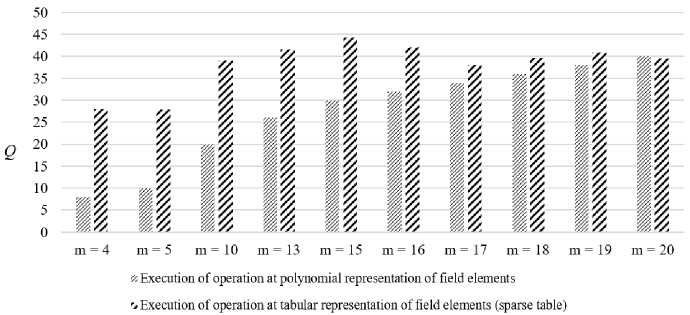
Fig.4. The number of elementary operations during the multiplication of field elements of GF (2 ^m )

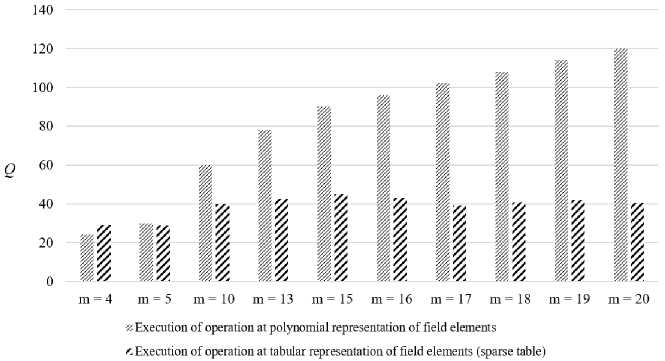
Fig.5. The number of elementary operations during the division of field elements of GF (2 ^m )

Fig. 6 shows the graph of the increase in speed (the ratio of the number of bit operations for a classic method which uses only polynomial representation and the proposed method) for the exponentiation operation depending on the chosen field (for the developed method, the degree of sparsity 16 was chosen).

It is experimentally established that the optimal degree of sparsity in the table is the value of 8, which provides an average increase in speed of 15% compared to the use of a polynomial basis.

Concluding from the above diagrams, the proposed method is characterized by a weak dependence of the number of shift and bitwise addition operations from the field parameter m to perform the calculation of the multiplicative inverse element and division operation. For the multiplication operation, the proposed method reduces the number of operations only starting from the value m = 20. In addition, it is noteworthy that with an increasing value of m at a fixed degree of sparsity, the advantage of the proposed method becomes more significant.

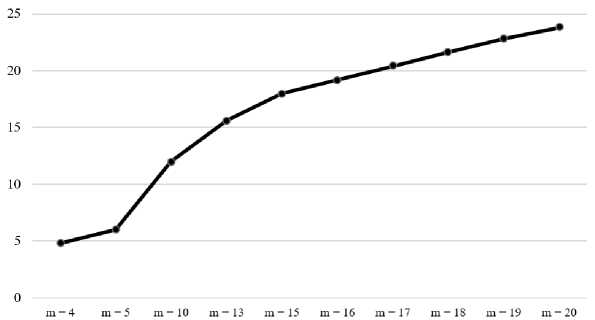
Fig.6. Increase in speed when performing the exponentiation operation of the field elements of GF (2 ^m )

7.    Conclusions

The analysis of mathematical operations on the elements of GF (2 ^m ) showed that the feature of GF (2 ^m ) is that the different forms of representation of the field elements are isomorphic, namely such that replace each other, in particular using exponential and numerical representation. The exponential representation is advisable to use for multiplicative operations, such as multiplication, division, and calculation of the multiplicative inverse element, and the polynomial representation for additive operations, such as addition and subtraction. The disadvantage of exponential representation is that it does not allow to obtain the zero element of the field.

The research showed that the most rational is the tabular method of performing operations on the elements of GF (2 ^m ) while storing the correspondence between the polynomial and the exponential representation of the field elements. A table consisting of two parts is used: the left part of the table is used to convert a numeric representation to exponential, and the right part – exponential to numeric, due to which it is possible to perform operations on all field elements, including the zero element.

If the field power is high, it is possible to not store all the field elements in the table, and form a sparse table, namely save only the basic elements of the whole table, which reduces memory costs for its storage. This is possible due to the finiteness of the field and the cyclical nature of the degrees of exponential representation of the field elements.

Any inverse mathematical function can be used to sparse a table. With this choice of function, it is possible to restore any element of a whole table with a base element. As a sparsity function, it is advisable to choose the function of division by a constant.

Thus, this article solves the urgent problem of improving existing methods of performing operations on the elements of GF (2 ^m ).

A method of high-speed addition and multiplication operations on elements of GF (2 ^m ) is proposed, which provides a speed increase of more than 4 times.

Due to the sparse tabular storage of field elements in their polynomial and exponential representation, the maximum speed is ensured.

The scientific novelty is that the method of obtaining the upper estimate of the number of elementary single-cycle operations for the methods of multiplicative inverse element calculation and the exponentiation operation in GF (2 ^m ). The optimal values of the sparsity degree of the table of elements of GF (2 ^m ) are obtained. For the multiplicative inverse element calculation for the value m = 20, the proposed method gives an increase in speed of almost 4 times, and for the exponentiation operation – almost 25 times.

The practical value of the obtained results is that the software is developed, which implements the proposed method and existing methods of operations on the elements of GF (2 ^m ) and allows the analysis of algorithms that implement these methods. Using this software, the practical problem of choosing the best algorithm for performing operations on GF (2 ^m ) field elements for use in encryption, digital signature, and error-correcting encoding algorithms can be solved.

The prospect for further research is the construction of a mathematical function for the sparsity of tables, which will reduce the computational complexity of the algorithm for converting the numerical representation of the field elements to exponential.